Inspired by graphene, two-dimensional (2D) nanoscale materials are now experiencing a great surge of research interest in the field of materials science and physics because of their intriguing nanoscale structure and novel electronic and magnetic properties for applications in future nanoelectronic devices.^[1–6] During the process of searching for promising materials, layered transition-metal dichalcogenides have been important members of the 2D materials. Mo and X (X = S, Se, Te) consist of stacked X–Mo–X layers, where the hexagonally packed transition metal Mo atom is typically trigonal prismatic coordinated with chalcogenide atoms X. The Mo–X bonds within one layer are covalent, but the sandwich layers are coupled only by weak van der Waals interaction,^[7–9] resulting in easy cleavage of planes. Theoretical studies have revealed that indirect gap semiconductors 2H–MoX₂ become direct gap semiconductors with significantly larger gap energy than those of the bulks when thinned to a single layer.^[10–16] Very recently, a long spin lifetime of more than 1 ns has been detected in polarization-resolved photoluminescence measurements,^[17] demonstrating that the spin lifetimes in the MoS₂ have outpaced that in graphene. This is because the spin–orbit coupling (SOC) and absence of inversion symmetry in MoS₂ suppress spin relaxation and hence, enhances the spin lifetimes.^[18] Compared to the MoS₂, MoTe₂ has a stronger SOC and a smaller direct energy band gap (1.1 eV)^[19] in monolayer (ML), which is considered to be used for ideal valleytronic and optical devices.^[20,21]

However, single material systems with restricted properties limit the development and application of the 2D materials. To date, more and more studies of TMDs are concerned with heterostructure systems.^[22] One can explore an abundance of the electronic properties by stacking TMDs with metal materials.^[20] In photodetection applications, the metal–TMD interface plays an active role of enhancing photoresponse.^[23] The surface Co atoms tend to form highly stable ferromagnetic states and exhibit a 100% current polarization (half-metal) in the newly formed Co/MoS₂ heterostructure.^[24] Rashba spin-splitting of electronic bands is found in MoS₂/Bi hybrid systems.^[25]

Nanoscale metal–semiconductor structure materials occupy an important position in semiconductor and microelectronic field due to their abundant physical phenomena and effects. The ultrathin films of the heavy metal interfaced with a semiconductor substrate have received increasing attention.^[26–28] By first-principles calculations, our previous work^[29] has found that extremely large Rashba spin-splitting (about 350 meV) appears in the ultrathin Pb(111)/MoTe₂ heterostructure. The lattice mismatch at the interface of this hybrid system is very small due to the same hexagonal structure and the nearly same lattice constants of two materials. However, the electronic devices are often fabricated with two metal contacts and form a metal–semiconductor–metal structure. So here in this work, we construct ultrathin Pb(111)(1 ML)/MoTe₂(1 ML)/Pb(111)(1 ML) heterostructure, which has the mirror symmetry. One of the motivation of this work is to study the different behavior of Rashba spin-splitting from that in asymmetry Pb(111)/MoTe₂ heterostructure. Furthermore, many 2D materials have been found to be superconductors.^[26,30–33] Pb is a conventional superconductor, so we want to know if superconductivity also appears in this ultrathin Pb(111)(1 ML)/MoTe₂(1 ML)/Pb(111)(1 ML) heterostructure. This is another motivation of this work. If large Rashba spin-splitting and superconductivity coexist, this heterostructure will have some novel quantum effects and specific applications. In this paper, we will systematically investigate the electronic structure and lattice dynamics of a heterostructure composed of 1-ML-MoTe₂ and Pb by using the first-principles method. The electron–phonon (EP) interaction and the superconducting properties are studied by using the fully anisotropic Migdal–Eliashberg theory powered by Wannier–Fourier interpolation.

The optimized norm-conserving Vanderbilt pseudopotential^[34] method is used with the PWSCF program of the Quantum-ESPRESSO distribution.^[35] The Perdew–Burke–Ernzerhof (PBE) formulation of the generalized gradient approximation (GGA) pseudopotential, with SOC included is employed to describe the electron–electron exchange and correlation energies.^[36] The highest kinetic energy in the plane-wave basis set is 80 Ry (1 Ry = 13.6056923(12) eV). Ultrathin Pb(111)/MoTe₂/Pb(111) is modeled by using the slab, 20-Å vacuum layers are set in order to avoid the interaction between layers. Electronic and vibrational states are computed by sampling the Brillouin zone on (12,12,1) and (6,6,1) grids, respectively. Maximally localized Wannier functions are determined by the WANNIER90 program.^[37] For the initial projection, we use the d orbitals for the Mo atom and sp³ hybrid orbitals for Pb and Te atoms. The electron energies, phonon frequencies and EP matrix elements on fine grids are obtained by using the Wannier–Fourier interpolation technique. The fine grids of k and q points are (48, 48, 1) and (24, 24, 1), respectively. The EPW program^[38] is used to perform the subsequent EP interpolation and solve the anisotropic Eliashberg equations. The technical details of these calculations are described in Ref. [38].

The stable geometric structure of 1-ML-MoTe₂ at ambient conditions is the 2H phase.^[39] The Te atoms are arranged in a trigonal prismatic coordination of Mo atoms and the stacking of atomic planes is an/ABA/sequence. For the Pb/MoTe₂/Pb heterostructure, because of the very small lattice mismatch, a surface (1 × 1) cell is used. The top and side views of the structure of Pb/MoTe₂/Pb heterostructure are sketched in Figs. 1(a) and 1(b). It has mirror symmetry with the Mo layer as the center plane. There are three possible sites (T₁, T₂, H₃) occupied for the contacted Pb atoms. The T₁ (T₂) site is on the Mo (Te) atom. The H₃ site is on the hollow center of the 2H hexagonal lattice. According to the calculations of the total energy after structural relaxation, the energy for H₃ site is lower than that in T₁ (T₂) site by 0.036 (0.035) eV. In the following calculations, we will only study the H₃ configuration. The stacking sequence of this configuration is |CABAC|, as labeled in Fig. 1(b). Our optimized lattice constant of the heterostructure is 3.524 Å, which is very close to the experimental lattice constant of MoTe₂ (3.52 Å).^[40] The interlayer distance D between Pb and 1-ML-MoTe₂ is D = 2.947 Å, which is much smaller than interlayer distance (3.522 Å) of the bulk MoTe₂. After 1-ML-MoTe₂ is in contact with Pb, the bond length between Mo and Te (d) is increased by 1.23%. This is due to a charge transfer at the interface, which weakens the covalent bond between Mo and Te atoms.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Schematic crystal structures: (a) Top and (b) side views of the Pb/1ML-MoTe2/Pb heterostructure.

For Pb/MoTe₂/Pb heterostructure, the band structure along some high symmetry directions is shown in Fig. 2(a). The corresponding Fermi surface is shown in Fig. 2(b). The green triangles in Fig. 2(a) indicate the contribution from Pb atom. The marker size is proportional to its electron density. It can be clearly seen that the bands near the Fermi energy (E_F) are mainly contributed by Pb. After spin-splitting, there are four conduction bands and four valence bands crossing the Fermi level. The Fermi surface consists of two nearly double degenerate circle-like hole pockets centered around the zone center ( point). Around the zone corner ( point), there are four arc-type electron pockets. Furthermore, the Fermi surface consists of two boat-like electron pockets at a point between and . The band projection shows a strong hybridization between the p_z orbital of Pb and d_z² of Mo for the hole bands near point. The electron bands near the point are mainly derived from in-plane orbitals.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) (a) The band structure of the Pb/MoTe2/Pb heterostructure along some high symmetry directions. Inset: out-of-plane spin-polarization bands around and points; (b) the Fermi surface of the Pb/MoTe2/Pb heterostructure.

The spin-splitting, i.e., the Rashba effect, originates from the strong SOC and space inversion asymmetry. The Pb/MoTe₂/Pb heterostructure has no space inversion symmetry, but it has center mirror symmetry. The out-of-plane potential gradient equals zero, so in-plane spin polarization disappears, and it only has out-of-plane spin-polarization. This is different from the case in the asymmetric Pb/MoTe₂ heterostructure. Due to the time reversal symmetry between the and points (labeled in Fig. 2(b)), the out-of-plane spin-polarization orientation is reversed. The largest spin-splitting occurs in the two lowest conduction bands at the or points and the corresponding spin-resolved band structures are sketched in the inset of Fig. 2(a). The values of two spin-splittings are about 364 meV and 263 meV, as sketched in Fig. 2(a).

The calculated phonon spectrum and the total phonon densities of states (DOS) F(ω) for the Pb/MoTe₂/Pb heterostructure are shown in Figs. 3(a) and 3(b). We can see that there is no imaginary frequency in the full phonon spectrum, which indicates its dynamical stability. In general, the acoustic modes and the interlayer modes between Pb and MoTe₂ are often in the low-frequency range, while the Mo–Te bond-stretching modes within the monolayer MoTe₂ are often in the high-frequency range. The calculated projected phonon DOS for the single atom is shown in Fig. 3(d). Due to the large difference of mass of the three atoms, their contribution to the phonon DOS is separated. The vibrations of Pb (Mo) atoms occupy below 6 meV (above 23 meV), while the vibrations of Te atoms occupy the middle frequency region. At the side of high-frequency, the vibrations of Mo and Te atoms are coupled.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) (a) Phonon spectrum; (b) total phonon density of states of the Pb/MoTe2/Pb heterostructure; (c) Eliashberg function α2F(ω) with integrated EP coupling constant λ(ω); and (d) projected phonon DOS for the Pb/MoTe2/Pb heterostructure.

Within the isotropic Eliashberg theory, the spectral function α²F(ω) can be given by^[41,42]

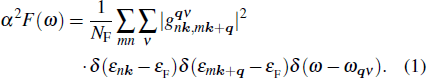To study the anisotropy in the EP couping, we evaluate the crystal momentum k and the band index n-dependent EP coupling λ_nk, which is given by

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) (a) The distribution of λnk for Pb/MoTe2/Pb heterostructure. (b) The variation of λnk on the Fermi surface, the data points correspond to electrons within ±200 meV from the Fermi energy.

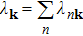
The superconducting properties of the Pb/MoTe₂/Pb heterostructure are obtained by solving the following anisotropic Migdal–Eliashberg equations^[43–46]

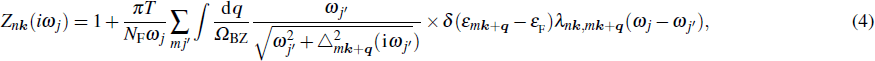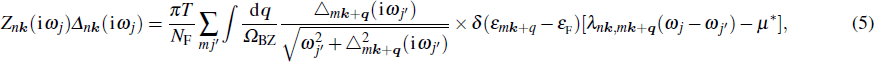The superconducting gap Δ_k on different parts of the Fermi surface at 1 K is shown in Fig. 5(a). We find that the distribution feature is very similar to that for EP coupling parameter λ_k shown in Fig. 4(b). It also displays a significant anisotropy. Figure 5(b) shows the superconducting energy gap Δ_k as a function of temperature, calculated for a screened Coulomb parameter μ^* = 0.1. The average value of the gap at each temperature is shown by square and Δ₀ is about 1.10 meV in the T = 0 K limit. The superconducting T_c is identified as the highest temperature at which the gap vanishes. From Fig. 5(b) we obtain T_c = 6.5 K. This value is larger than the value (T_c = 5.6 K) when Allen–Dynes equation is used to estimate the superconducting transition temperature. Our obtained ratio α = Δ₀/k_BT_c = 1.955, which is larger than the ideal BCS value of 1.764.^[49] The BCS gap equation is given by^[50]

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. (color online) (a) The superconducting gap at 1 K within ±200 meV from the Fermi energy, (b) energy distribution of the anisotropic superconducting gap Δk of Pb/MoTe2/Pb heterostructure as a function of temperature, (c) calculated superconducting critical temperature as a function of the Coulomb parameter μ*, and (d) calculated superconducting gap at the Fermi level in the T = 0 K limit as a function of the Coulomb parameter μ*.

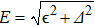
The Pb/MoTe₂/Pb heterostructure is a low-dimensional system with A complex Fermi surface, so the isotropic Migdal–Eliashberg equation is inadequate. Our calculated results show that the EP interaction has significant anisotropy. The temperature dependence of the superconducting gap can be fitted by solving the BCS gap equation numerically, but with an adjustable parameter α. These results provide support for a conventional phonon-mediated mechanism as the superconducting origin. Furthermore, in the Pb/MoTe₂/Pb heterostructure, the spin-splitting is completely out-of-plane and opposite at the and points, and we find that the value of the spin-splitting near point is much larger than the superconducting gap. This case is very similar to the case in monolayer transition metal dichalcogenides, the pairing state can be interpocket pairing (spin-singlet) or intrapocket pairing (spin-triplet) as suggested by Hsu et al.,^[51] which suggests that the Pb/MoTe₂/Pb heterostructure may be a candidate for topological superconductors. Artificially engineered topological superconductivity in hybrid structures is currently attracting significant attention. Experimentally, proximity-induced superconductivity at the edges of nanowires has been studied by many groups and there is accumulating evidence in the search for Majorana fermions.^[52,53] Regarding the semiconductors with Rashba-split bands, there has been no experiment so far on a 2D system according to the best of the author’s knowledge. The Pb/MoTe₂/Pb heterostructure may be of interest for further experimental study.

In summary, we have investigated the peculiar electronic structures of the Pb/MoTe₂/Pb heterostructure by using density-functional theory. Due to strong SOC and space inversion asymmetry, large Rashba spin-splitting of electronic bands appears in this hybrid system. We have also studied superconducting properties of the Pb/MoTe₂/Pb heterostructure within the anisotropic Migdal–Eliashberg theory. Due to the complex Fermi surface in this low-dimensional system, the EP interaction and the superconducting gap display significant anisotropy. The temperature dependence of the superconducting gap can be fitted by solving the BCS gap equation numerically, but with an adjustable parameter α, suggesting a phonon-mediated mechanism as its superconducting origin. The spin-splitting near the point is much larger than the superconducting gap, implying that the Pb/MoTe₂/Pb heterostructure may be a candidate for topological superconductivity.