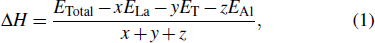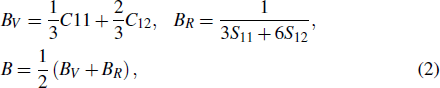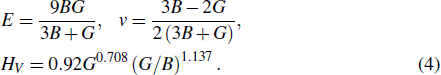1. IntroductionAluminum alloys have been playing an important role in many industrial fields due to their outstanding physical properties.[1] But the poor creep-resistance properties of aluminum alloys have hindered their wide applications at high temperatures. In the past few decades, many researchers found that the addition of appropriate transition metal elements (TM) and rare earth elements (RE) to aluminum alloys can form L12, D022, D023 or D019-ordered binary Al3TM and Al3RE intermetallics. These binary intermetallics exhibit some outstanding physical properties, including low mass densities, high melting points, and good oxidation resistances, and so on, which can effectively improve the poor creep-resistance of aluminum alloys.[2–15] In the meantime, some ternary AT2Al20 intermetallics systems (where A = actinide/lanthanide/calcium and T = transition metal) were synthesized with CeCr2Al20-type structure.[16–32] Kangas and Thiede synthesized the new LaT2Al20 (T = Ti, V, Cr, Nb, and Ta) intermetallics by using a step-wise arc melting technique and by self-flux method.[31,32] For these new LaT2Al20 phases, although their intrinsic physical properties have been explored, their mechanical properties and thermodynamics properties are not clarified. It is necessary to investigate the related physical properties for further applications. In the present work, the first-principles calculations were used to comparatively investigate the structural stability, mechanical, and thermodynamics properties for Al and LaT2Al20 intermetallics.
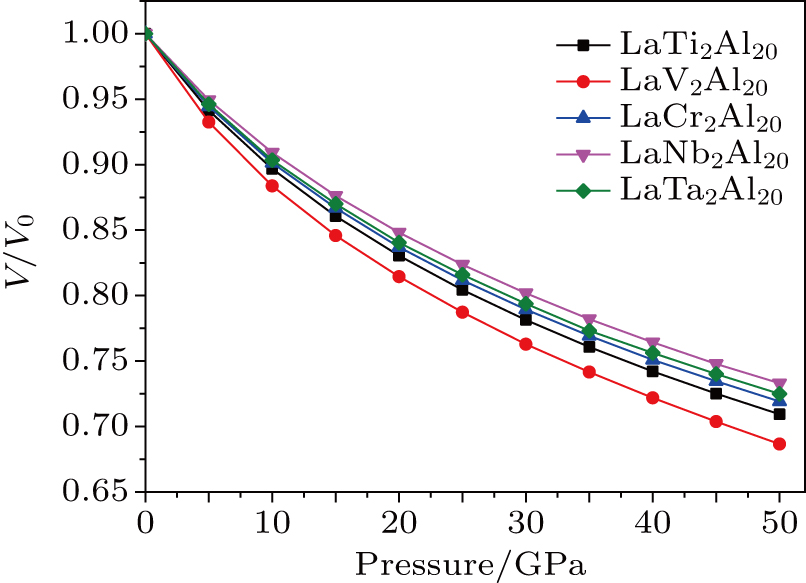
3. Results and discussion3.1. Structural stabilityLaT2Al20 intermetallics can crystallize in the face-centered cubic structure with Fd-3m space group. In the prototypic LaT2Al20 compounds, La atoms occupy the 8a Wyckoff sites, T atoms occupy the 16d Wyckoff sites, and Al atoms occupy the 16c, 48f, and 96g Wyckoff sites. The unit cell of structure is shown in Fig. 1.[25] The optimized atom coordinates are listed in Table 1, together with experimental ones. In the meantime, the ratios of volume change (V/V0) under different pressures were shown in Fig. 2. In Table 1, the calculated data are slightly larger than experimental ones[31,32] and the error is less than 5%, which indicates that the computational method is reliable. LaNb2Al20 has the largest bulk modulus B0 among five intermetallics, which indicates the LaNb2Al20 has the best ability to resist the compression. In Fig. 2, the curves of V/V0 are smooth and have no inflection points until 50 GPa, which indicates that these intermetallics can keep structural stability under high pressures. The curves of LaNb2Al20 and LaV2Al20 locate at upper part and lower part, which indicates that LaNb2Al20 and LaV2Al20 have the best/worst resistance ability to compression among five compounds.
Generally speaking, the structural stability of the solid materials mainly depends on two conditions: one is thermodynamic condition, which depends on the formation enthalpy; the other is the dynamical condition, which depends on the phonon frequencies.[36,37] The formation enthalpy was calculated using the following expression[38–41]
where
ETotal represents the total energy of La
T2Al
20;
x,
y, and
z are the numbers of atoms in the unit cell;
ELa,
ET, and
EAl represent the total energy of per atom in solids. The calculated formation enthalpies Δ
H for La
T2Al
20 are all negative values in Table
1, indicating that La
T2Al
20 compounds have the stronger thermodynamic stability and is more inclined to form LaTa
2Al
20 due to the lower value of Δ
H.
Table 1.
Table 1.
 Table 1. The lattice constant a0, bulk modulus B0 and formation enthalpy. ΔH of LaT2Al20 (T = Ti, V, Cr, Nb, and Ta) intermetallics. .
| Compounds |
a/Å |
B0/GPa |
ΔH/(eV/atom) |
|
| LaT2Al20 |
14.912 |
78.192 |
–0.3213 |
this work |
|
14.7713 |
|
|
Exp.[31] |
| LaT2Al20 |
14.788 |
65.665 |
–0.3325 |
this work |
|
14.60 |
|
|
Exp.[31] |
| LaCr2Al20 |
14.632 |
87.026 |
–0.3334 |
this work |
|
14.45 |
|
|
Exp.[32] |
| LaNb2Al20 |
15.062 |
88.367 |
–0.3395 |
this work |
|
14.811 |
|
|
Exp.[32] |
| LaTa2Al20 |
15.081 |
88.012 |
–0.3398 |
this work |
|
14.811 |
|
|
Exp.[32] |
| Table 1. The lattice constant a0, bulk modulus B0 and formation enthalpy. ΔH of LaT2Al20 (T = Ti, V, Cr, Nb, and Ta) intermetallics. . |
In order to explore the dynamical stability, the phonon dispersion and the density of states are calculated in Figs. 3 and 4. The solid lines are calculated values and the scatter points are experimental ones of the inelastic neutron scattering measurement in Fig. 3.[42] The calculated values are close to the experimental ones, which indicate that the calculated results are reasonable. Figure 4 shows the phonon dispersion curves and the density of states for LaT2Al20 intermetallics. For five figures of phonon dispersion curves, the imaginary phonon frequencies are absent along the Brillouin zone path. It indicates that the five compounds possess the dynamical stability. Figure 5 displays the total phonon density of states for LaT2Al20 intermetallics. For the phonon density of states (PHDOS), the imaginary frequencies are also absent. It indicates that the five compounds possess the dynamical stability. In summary, according to the obtained formation enthalpies and phonon frequencies, the five intermetallics exhibit the structural stability.
3.2. Elastic propertiesThe elastic constants and elastic moduli are important parameters for engineering applications. Table 2 listed the calculated elastic constants Cij and compliance matrices Sij, together with the experimental values of pure Al for comparison.[43–45] The elastic constants of Al are consistent with experimental ones (as shown in Table 2). The calculated results indicate that our computational method is reliable. For the cubic structure intermetallics, there are three independent constants C11, C12, and C44. The elastic constants are satisfied with the mechanically stable conditions:[46] C11 ˃ 0, C44 ˃ 0, C11 ˃ |C12|, (C11 + 2C12)˃ 0. After obtaining the elastic constants Cij and Sij, the bulk modulus B, shear modulus G, Young’s modulus E, and hardness Hv were calculated by using the VRH method with the following equations[46]
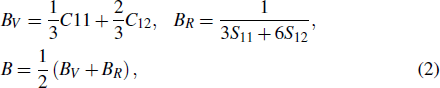 | |
 | |
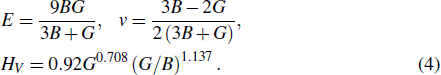 | |
The calculated elastic moduli of LaT2Al20 are listed in Tables 3 and 4, together with the experimental ones of Al.[43,45] The bigger values of bulk modulus B and shear modulus G correspond to the better resistance of solid materials against volume change under hydrostatic pressure and shape deformation by the shearing force. In Table 3, the values of elastic modulus B follow the order: LaNb2Al20 ˃ LaTa2Al20 ˃ LaCr2Al20 ˃ Al ˃ LaTi2Al20 ˃ LaV2Al20, this indicates that LaNb2Al20 has the best ability of resistance to the volume deformation. The values of elastic modulus G follow the order: LaNb2Al20 ˃ LaTa2Al20 ˃ LaCr2Al20 ˃ Al, indicating that LaNb2Al20 has the best ability of resistance to shape change under external conditions. Five LaT2Al20 intermetallics have the stronger shear deformation resistance in comparison with the pure Al. The larger elastic constants C44, elastic modulus G, and E correspond to the higher hardness of solid materials. The values of C44, G, and E of five intermetallics are remarkably larger than the ones of pure Al, indicating that these ternary intermetallics possess the higher hardness than the pure Al. In the meantime, for LaTi2Al20, LaV2Al20, LaCr2Al20, LaNb2Al20, LaTa2Al20, and Al, the values of hardness are also calculated by using the semi-empirical equations with Eq. (4): 12.249 GPa, 12.191 GPa, 7.747 GPa, 12.590 GPa, 9.359 GPa, and 2.868 GPa. The calculated results indicate the LaT2Al20 compounds are harder than Al.
Table 2.
Table 2.
 Table 2. Calculated elastic constants Cij (in unit GPa) and compliance matrices Sij. .
| Model |
|
C11 |
C12 |
C44 |
S11 |
S12 |
S44 |
| LaTi2Al20 |
Cal. |
141.449 |
44.034 |
66.931 |
0.0083 |
–0.0020 |
0.0149 |
| LaV2Al20 |
Cal. |
124.607 |
34.377 |
62.276 |
0.0091 |
–0.0019 |
0.0161 |
| LaCr2Al20 |
Cal. |
143.979 |
55.504 |
52.519 |
0.0088 |
–0.0025 |
0.0190 |
| LaNb2Al20 |
Cal. |
174.569 |
42.241 |
63.331 |
0.0063 |
–0.0012 |
0.0158 |
| LaTa2Al20 |
Cal. |
144.699 |
56.808 |
63.479 |
0.0089 |
–0.0025 |
0.0158 |
| Al |
Cal. |
112.091 |
63.424 |
32.065 |
0.0151 |
–0.0055 |
0.0312 |
| Al[43] |
Exp. |
124 |
61.9 |
31.6 |
|
|
| Al[44] |
Exp. |
109 |
64.5 |
32.4 |
|
|
| Al[45] |
Exp. |
108 |
62 |
28 |
|
|
| Table 2. Calculated elastic constants Cij (in unit GPa) and compliance matrices Sij. . |
Table 3.
Table 3.
 Table 3. Calculated elastic moduli (in unit GPa) B, G, E, B/G, Hv, and Poisson’s ratio v. .
| Model |
B |
G |
E |
B/G |
Hv |
v |
| LaTi2Al20 |
76.506 |
58.930 |
140.671 |
1.298 |
12.249 |
0.194 |
| LaV2Al20 |
64.453 |
54.732 |
127.972 |
1.178 |
12.191 |
0.169 |
| LaCr2Al20 |
84.996 |
49.033 |
123.375 |
1.733 |
7.747 |
0.258 |
| LaNb2Al20 |
86.350 |
64.450 |
154.828 |
1.339 |
12.590 |
0.201 |
| LaTa2Al20 |
86.105 |
54.781 |
135.588 |
1.572 |
9.359 |
0.237 |
| Al |
79.646 |
28.711 |
76.893 |
2.774 |
2.868 |
0.339 |
| Al Exp |
79.3[43] |
29.4[43] |
|
2.493[45] |
|
0.323[45] |
| Table 3. Calculated elastic moduli (in unit GPa) B, G, E, B/G, Hv, and Poisson’s ratio v. . |
Table 4.
Table 4.
 Table 4. Calculated bulk modulus BV, BR (in unit GPa), shear modulus GV, GR (in unit GPa), and elastic anisotropic factors. .
| Model |
BV |
BR |
GV |
GR |
AU |
A |
| LaTi2Al20 |
76.506 |
76.506 |
59.642 |
58.218 |
0.122 |
1.374 |
| LaV2Al20 |
64.453 |
64.453 |
55.412 |
54.052 |
0.126 |
1.380 |
| LaCr2Al20 |
84.996 |
84.996 |
49.206 |
48.860 |
0.035 |
1.187 |
| LaNb2Al20 |
86.350 |
86.350 |
64.464 |
64.435 |
0.002 |
0.957 |
| LaTa2Al20 |
86.105 |
86.105 |
55.665 |
53.896 |
0.164 |
1.444 |
| Al |
79.646 |
79.646 |
28.972 |
28.449 |
0.092 |
1.318 |
| Table 4. Calculated bulk modulus BV, BR (in unit GPa), shear modulus GV, GR (in unit GPa), and elastic anisotropic factors. . |
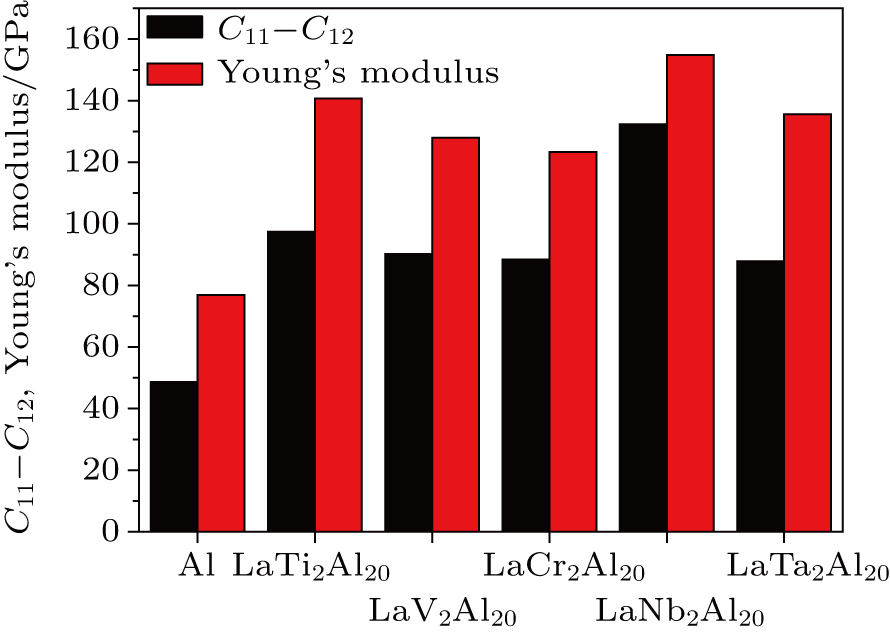
The ductile or brittle behavior influences the high temperature application of solid materials. The values of B/G ratio and Poisson’s ratio v can determine the brittle and ductile behaviors of solid materials. When the values of B/G and v are less than 1.75 and 0.26, the solid materials possess brittle behavior. Otherwise, the solid materials possess ductile behavior. The calculated values of B/G and v are shown in Table 3. The values of B/G and v of LaT2Al20 intermetallics are all smaller than the critical value 1.75 and 0.26, which indicates that LaT2Al20 intermetallics are all brittle materials. But Al possesses the ductile behavior because of the larger B/G and v values (2.774 and 0.339). In the meantime, LaV2Al20 has the smallest B/G and v, this indicates that it possesses the largest brittleness among these compounds. The values of elastic constants (C11–C12) and Young’s modulus are the criterion to estimate the plasticity of solid materials. Generally speaking, if the solid materials have the smaller values of elastic constants and Young’s modulus, they will possess better plasticity.[47] In order to intuitively describe the plastic behavior, the results of the LaT2Al20 compounds and the experimental ones for pure Al[45] are shown in Fig. 6. In Fig. 6, the pure Al has the best plasticity and LaT2Al20 compounds have the worse plasticity than the pure Al. In order to present the brittleness of LaT2Al20 compounds, figure 7 shows the renormalized hyperbolic correlation derived by (C12–C44)/E and G/B, including the calculated values of LaT2Al20 with some typical materials, Au, Pd, Al, Si, Ge, BN, diamond, and so on.[48] According to the Pugh criterion and Pettifor criterion, the LaT2Al20 compounds possess the brittle nature and high hardness, which is close to that of Si, Ge, and BN.
3.3. Anisotropic propertiesThe anisotropic properties are closely related to the micro-cracks behavior of solid materials. The anisotropic properties were described by the universal and shear anisotropic index AU and A[46]
The calculated anisotropic indexes AU and A are shown in Table 4. When the anisotropic values of AU and A approach to and 1 respectively, the crystalline phases possess the isotropic properties. The anisotropic data listed in Table 4 confirm that these compounds are anisotropic. The indexes AU and A correspond to the same order: LaTa2Al20 ˃ LaV2Al20 ˃ LaTi2Al20 ˃ Al ˃> LaCr2Al20 ˃ LaNb2Al20, which indicates that LaTa2Al20 has the largest anisotropy, but LaNb2Al20 possesses the smallest anisotropy. But the degree of anisotropy of LaT2Al20 compounds is small and LaNb2Al20 approaches to the isotropy.
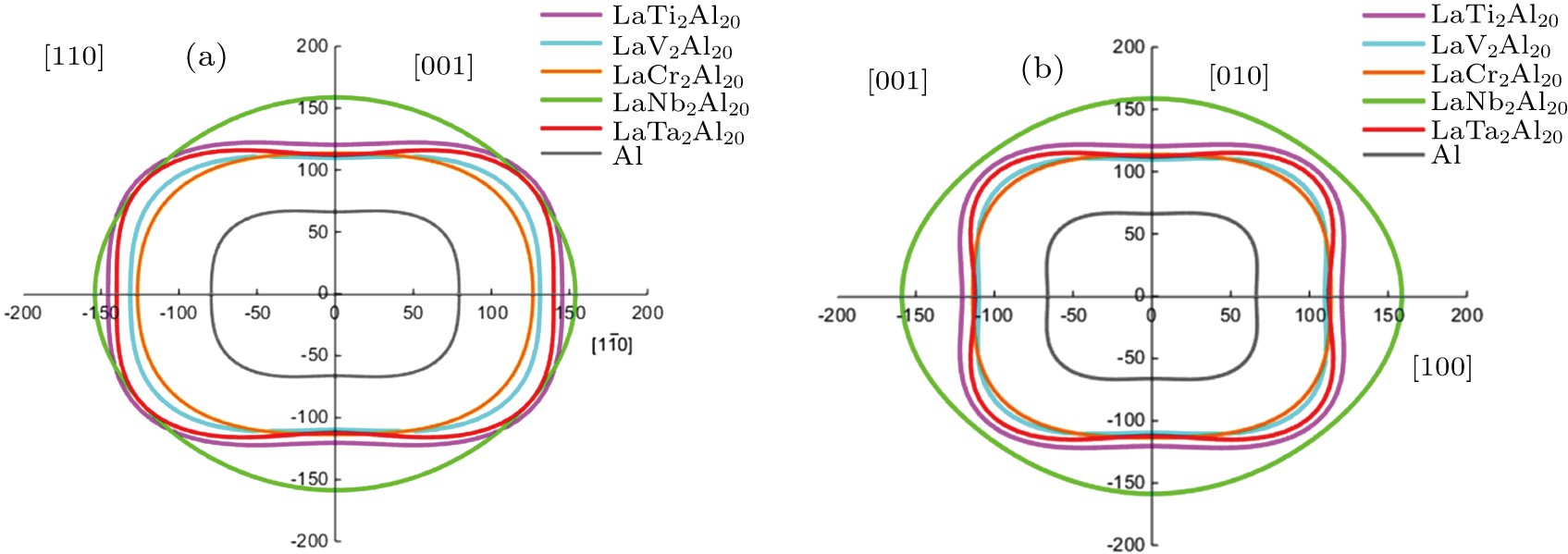
In order to visually describe anisotropic properties of LaT2Al20 intermetallics, the three-dimensional surfaces of Young’s modulus E was adopted to further explore the anisotropy of crystal phases. The three-dimensional (3D) figures were displayed using the following equation[46]
If the 3D surfaces of Young’s modulus are spherical, they will be isotropic. Otherwise, they are anisotropic. The greater the degree of deviation from the sphere is, the stronger the anisotropic properties are. The 3D figures of Young’s modulus are shown in Fig.
8. According to the degree of deviation from the sphere, it can be concluded that La
T2Al
20 intermetallics are all anisotropic. The degree of deviation from the sphere for LaNb
2Al
20 is smallest among six figures, suggesting that it is basically isotropic. On the contrary, LaTa
2Al
20 has the largest anisotropy. The figures of other compounds display the degree of deviation, but the degree of deviation is small, indicating that these intermetallics are anisotropic and the anisotropy is small. In order to furthermore describe the anisotropic properties of the La
T2Al
20 intermetallics, the two-dimensional figures of Young’s modulus on different planes are plot in Fig.
9. If the contours of the closed curves are circles, the crystal materials possess the isotropic properties. If the contours of the closed curves deviate from circles, the crystal materials possess the elastic anisotropy. In Fig.
9, the contours of the LaNb
2Al
20 are closed to circles, but LaTa
2Al
20 and Al possess the larger degree of deviation, indicating that LaNb
2Al
20 is more closed to the elastic isotropy.
3.4. Electronic and magnetic propertiesThe total density of states (TDOS) and partial density of states (PDOS) of LaT2Al20 from −12 eV to 4 eV are shown in Fig. 10. The dash line at zero energy represents the Fermi level EF in Fig. 10. There are no energy gaps near the Fermi level EF, indicating that five intermetallics exhibit metallic property. The region of energy binding states from about −12 eV to −4 eV in TDOS is determined mainly by Al 3s and 3p states. The energy binding states near the Fermi level EF are hybridized mainly by La 5d, T (Ti/V/Cr) 3d, and Al 3p states. The strong hybridization creates the pseudogap near the Fermi level in TDOS for five LaT2Al20 intermetallics. The strong hybridization can guarantee the electronic interaction between the atoms and improve the bond strength. LaT2Al20 intermetallics exhibit the better elastic properties than pure Al, which is attributed to the bond strength of La–Al, La–T, and T–Al metallic bonds of LaT2Al20 intermetallics. Comparing the up states with the down states of TDOS in Fig. 11, we found that the spin-down and spin-up states are not symmetric for LaCr2Al20 intermetallics, but the spin states of other four LaT2Al20 (T = Ti, V, Nb, and Ta) compounds are symmetric. It indicates that LaCr2Al20 intermetallics exhibit magnetic properties and other four LaT2Al20 compounds are non-magnetic compounds. The results are consistent with the experiments ones.[17,29,31]
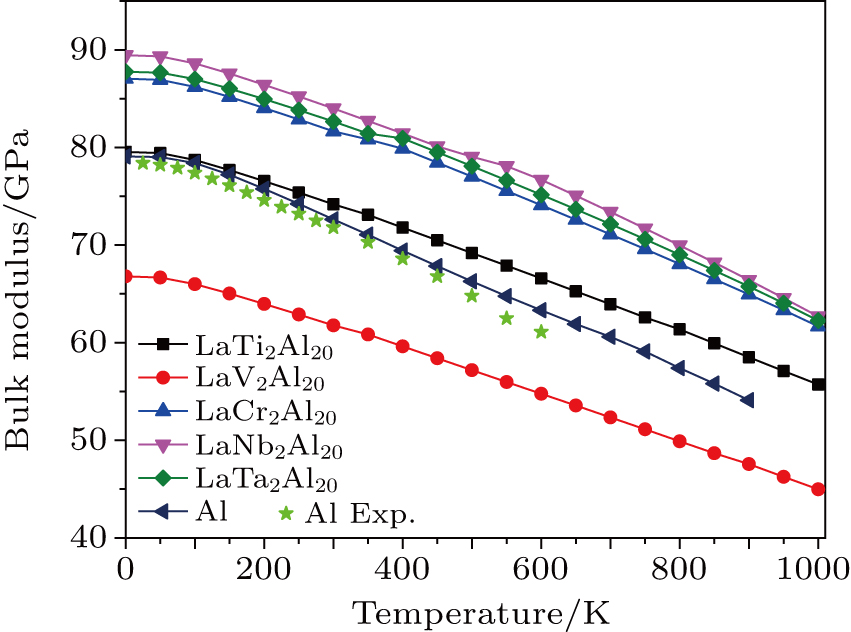
3.5. Thermodynamic propertiesFor cubic structural crystals, they have only one-independent lattice parameter. Thus, we performed the lattice dynamic calculations for the variable lattice parameter from 0.94a to 1.06a in a step of 0.01a within the PHONOPY code. By using F (V, T)–V data, we fit them to Vinet EOS and obtained the related thermodynamic parameters. The relationships between thermodynamic quantities and temperature for pure Al and LaT2Al20 intermetallics are shown in Figs. 12–15. Because the melt point temperature of Al is about 960 K, so we gave out the thermodynamic quantities between 0 K and 900 K for pure Al. Figure 12 shows the relationships between Gibbs free energy and the elevated temperature. The Gibbs free energy is negative and decreases gradually with increasing temperature, indicating that these compounds are thermodynamically stable in the whole temperature range. The smaller the Gibbs free energy is, the better the thermal stability of compound is. Five LaT2Al20 intermetallics exhibit the better thermal stability than pure Al in the high temperature section. Figure 13 shows the relationships between bulk modulus and the elevated temperature. It is clear that when the temperature is less than 100 K, the bulk modulus nearly remains constant, but it drops remarkably in the high temperature section. The change of bulk modulus of LaT2Al20 intermetallics is smaller than Al, indicating that the ability of creep resistance of LaT2Al20 intermetallics are better than pure Al. Figure 14 shows the relationships between thermal expansion coefficients and temperature. It is noted that the expansion coefficients increase exponentially in the low temperature section and increase slowly (approaches to the linear increases) in the high temperature regime. But in the high temperature section, the values of pure Al are remarkably larger than those of five LaT2Al20 compounds at a given temperature, indicating that the pure Al becomes easier to expand at high temperature. Figure 15 shows the relationships between entropy and temperature. The values of entropy of pure Al and RET2Al20 compounds rapidly increase almost linearly with the elevated temperature. In order to prove the correctness of our calculation method, we compared the theoretical values and the experimental ones[49–51] of bulk modulus and entropy of pure Al in Figs. 13 and 15. The calculated results are very close to the experimental ones, which indicate that the calculated method and results are reliable.