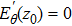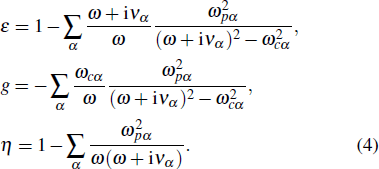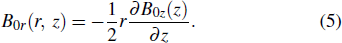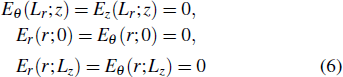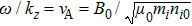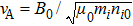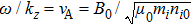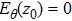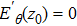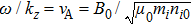1. IntroductionThe gap eigenmode of shear Alfvén waves (SAWs) has been observed extensively to expel energetic ions from magnetic confinement, which then damage the vessel components of fusion reactor.[1,2] As a result, understanding the formation mechanism of this gap eigenmode and characterizing its interaction with energetic ions are of critical importance to the success of magnetically confined fusion.[3,4] Benefiting from easy diagnostic access, simple geometry and low cost, plasma cylinder with low temperature is a promising candidate to study fundamental physics involved in traditional fusion devices. In 2008, Zhang et al.[5] observed a spectral gap in the Alfvénic continuum in experiments on Large Plasma Device (LAPD[6]) by constructing a multiple magnetic mirror array. However, the discrete eigenmode was not formed inside the gap. To guide the experimental implementation of this gap eigenmode, Chang et al. have been developing self-contained analytical theory and carrying out numerical computations first on the gap eigenmode of radially localized helicon (RLH) waves,[7] which can be excited by energetic electrons in a similar way, and then on the gap eigenmode of SAWs for ideal conditions.[8,9] The present work computes this gap eigenmode using exact LAPD parameters, including geometry, plasma density, electron temperature, field strength, effective collisionality and limited number of magnetic mirrors, etc. It will first give a full picture of the wave field for previous experiment, showing that the previously observed spectral gap is not global but an axially local result, and then clearly form gap eigenmodes for three cases: high field strength and plasma density, low field strength and plasma density and reduced number of magnetic mirrors. This preliminary computation can be a strong motivation and important reference for the experimental observation of the gap eigenmode of SAWs on the LAPD and other linear plasma devices.
The paper is organized as follows. Section 2 describes the numerical scheme and wave field for previous experiment, which also benchmarks the employed computations; Section 3 presents the spectral gap and gap eigenmode of SAWs based on the conditions which are achievable by the LAPD either with slight modulations or at its present status. Section 4 consists of discussion about continuum damping of this gap eigenmode and conclusions.
2. Numerical scheme and wave field for previous experimentThis section is devoted to first introducing the numerical scheme and employed conditions and then showing a full picture of the wave field for previous experiment, which also serves as a detailed benchmark.
2.1. Electromagnetic solver (EMS)An ElectroMagnetic Solver (EMS)[10] based on Max-well’s equations and a cold plasma dielectric tensor is employed to study the spectral gap of shear Alfvén waves and gap eigenmode inside. The Maxwell’s equations are expressed in the frequency domain:
where
E and
B are the wave electric and magnetic fields, respectively,
D is the electric displacement vector,
ja is the antenna current and
ω is the antenna driving frequency (same to wave frequency for this driven system). These equations are Fourier transformed with respect to the azimuthal angle and then solved (for an azimuthal mode number
m) by a finite difference scheme on a two-dimensional (2D) domain (
r;
z). The quantities
D and
E are linked via the cold plasma dielectric tensor
[11]
where
b ≡
B0/
B0 is the unit vector along the static magnetic field and
The subscript
α labels particle species (electrons and ions);

is the plasma frequency,
ωcα ≡
qαB0/
mα is the cyclotron frequency and
να is a phenomenological collision frequency for each species. The static magnetic field is assumed to be axisymmetric with
B0r ≪
B0z and
B0θ = 0.
[5,7] It is therefore appropriate to use a near axis expansion for the field, namely
B0z is only dependent on
z and
A blade antenna is employed to excite
m = 0 mode in the plasma, as chosen in the previous experiment.
[5] The enclosing chamber is assumed to be ideally conducting so that the tangential components of
E vanish at the chamber walls,
i.e.
with
Lr and
Lz the radius and length of the chamber, respectively. Further, all field components must be regular on axis. More details about the EMS can be found in Ref. [
10].
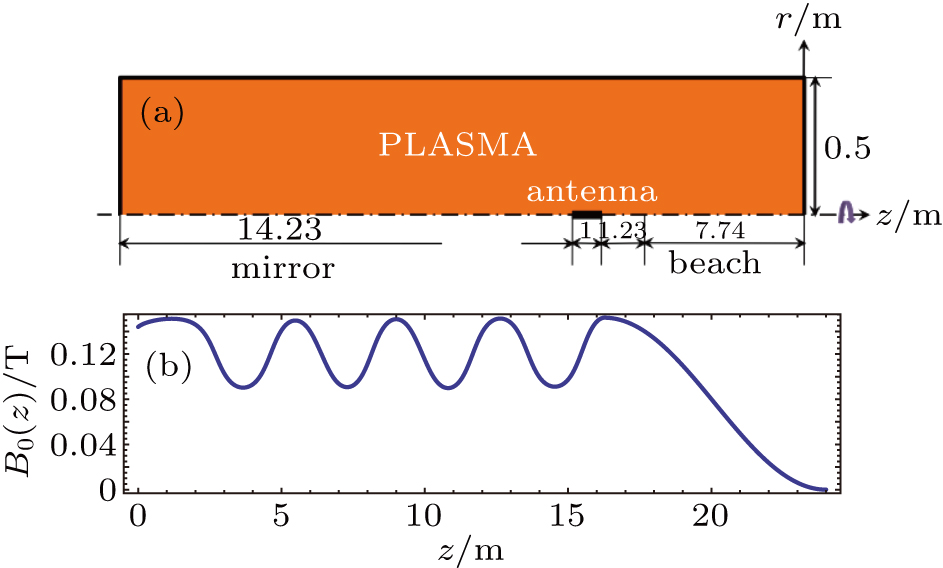
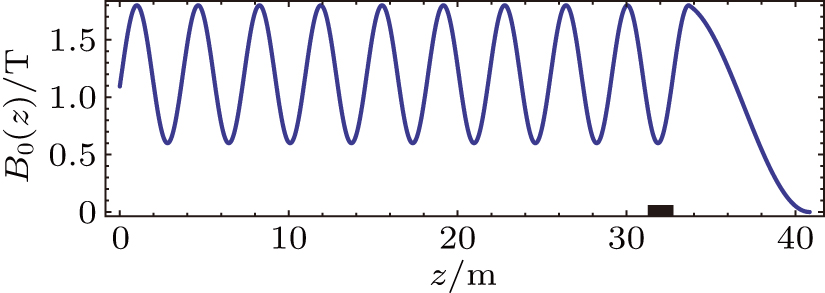
2.2. Wave field for previous experimentThe computational domain and configuration of static magnetic field are shown in Fig. 1, which are the same to those in Ref. [5] except that now the coordinate is from left to right for convenient simulations. As employed previously, a magnetic beach is constructed as an absorbing end, and it is longer 7.74 m (from z = 16.26 m to z = 24 m) than that in the experiment to ensure complete absorption; moreover, a finite ion collision frequency νi(z) has been introduced to resolve the ion cyclotron resonance in the beach area.[5] Other parameters are taken from experiment directly, including helium ion specie, electron temperature Te = 8 eV, plasma density ne = 9.2 × 1017 exp(−10.2 r2) m−3, blade antenna of length La = 1 m and radius Ra = 0.005 m, and diagnostic ports at z = 3.98 m and z = 11.02 m (or 10.25 m and 3.21 m respectively in the opposite coordinate).
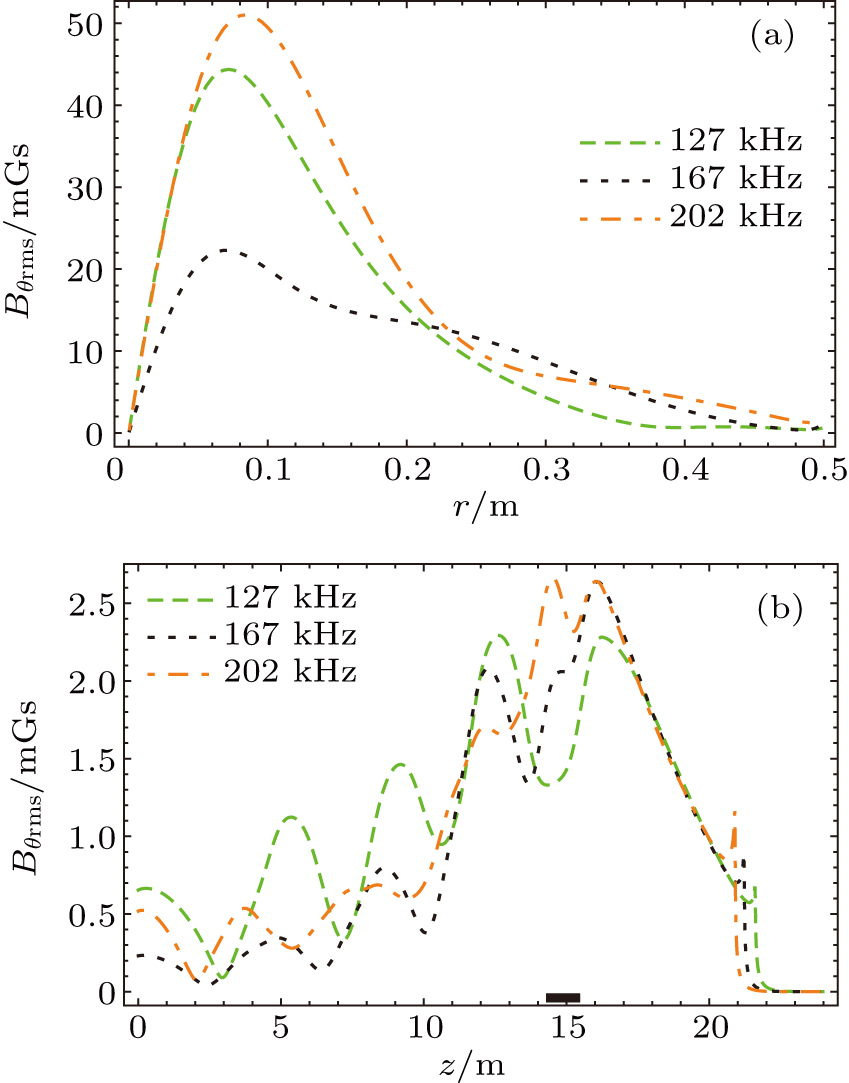
Figure 2 shows the variations of azimuthal wave magnetic field (rms) with radius and axis for three typical frequencies: 127 kHz, 167 kHz, and 202 kHz. The radial profiles and magnitudes of Bθrms are identical to those previously published (Fig. 14 in Ref. [5]), which exhibit a spectral gap centered around 167 kHz and state the credibility of present simulations. The axial profiles of Bθ rms display a standing wave structure or beat pattern, implying strong reflections from the left endplate. Due to ion cyclotron resonance, the magnitude of Bθ rms decays quickly around z = 21 m. A full picture of the wave field in the LAPD plasma is given by Fig. 3 in the spaces of (f; r) and (f; z). A strong and robust radial structure can be seen clearly from the (f; r) space for different driving frequencies. However, a global spectral gap is not distinct in the (f; z) space, which is surprising and indicates that the spectral gap observed in Fig. 2(a) (also Fig. 5 below) may be an axially local result.
This can be further confirmed by comparing the variations of peak wave magnitude (rms) with frequency at two axial locations, namely z = 3.98 m and z = 11.02 m, as shown in Fig. 4. The values of α represent possible estimates of effective collision frequencies for Landau damping. The total effective collision frequency is termed as νeff = νei + νe−Landau with νe − Landau = αvtheω/vA.[5] Except where acknowledged, α = 4 is used throughout the whole paper, and the Coulomb collision between ions and electrons νei is believed to be the leading collision process affecting the energy deposition. The gap profiles measured at z = 3.98 m are much better than those at z = 11.02 m which exhibit nearly no spectral gap. Again, the curves in Fig. 4 are identical to those in Fig. 15 in Ref. [5], stating the credibility of the employed computations.
Figure 5 displays the contour plots of wave energy density and power deposition density for three typical frequencies: 120 kHz, 170 kHz, and 220 kHz. Although figure 5(a) shows a spectral gap centered around 170 kHz, it is not thorough because waves can still propagate a distance (near the left endplate). This is also confirmed by the power deposition density shown in Fig. 5(b), which is directly relevant to the wave field through energy conservation but does not show a clear spectral gap. The reason that this spectral gap is not thorough and global may be due to very few magnetic mirrors and small modulation depth employed in the previous experiment. Moreover, the experimentally constructed magnetic mirror array shown in Fig. 1(b) is not perfectly periodic. The axial length of each mirror is not exactly 3.63 m but with 3%–18.7% difference, and the maxima and minima also have about 1% difference around 0.15 T and 0.09 T respectively. Although these differences are small, they can affect the dispersion relation of Alfvén waves significantly.
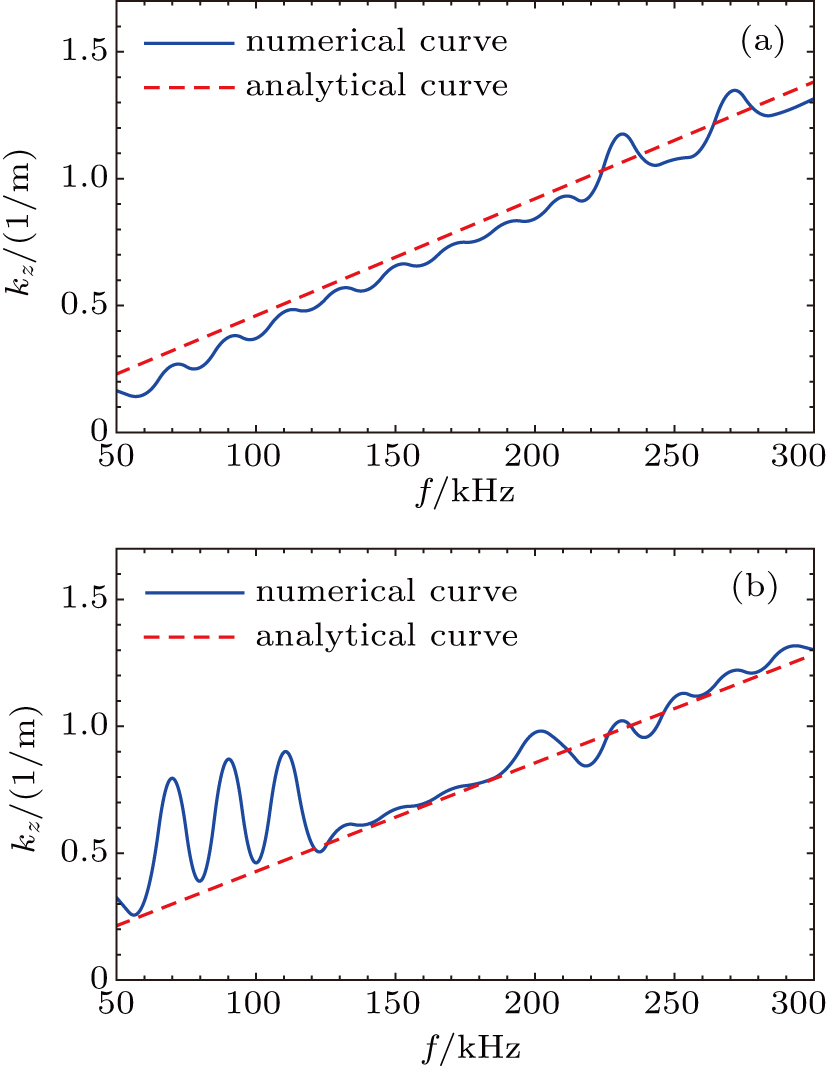
Figure 6 shows the dispersion curves for the experimental magnetic mirror shown in Fig. 1(b) and numerical magnetic mirror of B0(z) = 0.12 + 0.3 cos[2π(z − 16.84)/3.63], together with the analytical dispersion relation of
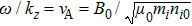 for uniform magnetic field (here ni0 is the plasma density on axis). It can be seen that the imperfect periodicity shifts the dispersion curve to lower frequency range and distorts the curve shape.
for uniform magnetic field (here ni0 is the plasma density on axis). It can be seen that the imperfect periodicity shifts the dispersion curve to lower frequency range and distorts the curve shape.
3. Global spectral gap and gap eigenmode3.1. High field strength and plasma densityBased on previous analyses, this section will increase the number of magnetic mirrors, which can be done only by increasing the length of mirror area due to the unchangeable minimum length of each mirror, namely 3.63 m on the LAPD, and construct the mirror field numerically with perfect periodicity. To broaden the width of spectral gap for easy gap eigenmode formation, the modulation depth will be increased as well according to Δω = εω0 in previous studies with ε the modulation depth.[5,7,8] Furthermore, because the collisional damping rate of Alfvén waves can be approximated as 3ω2νei/(2ωci|ωce|),[8,12] the magnitude of field strength will be increased to have large ion cyclotron frequency and thereby low Alfvénic damping rate. The final constructed periodic magnetic field is B0(z) = 1.2 + 0.6cos[2π(z − 33.68)/3.63]. The length of mirror area and modulation depth are doubled and the field strength is increased by 10 times. Here, to maintain the phase velocity of Alfvén waves for comparison with previous work, the plasma density is increased by 100 times (
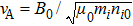 ). The numerically constructed magnetic field with absorbing beach is shown in Fig. 7. Figure 8 gives the surface plots of computed wave field in the spaces of (f; r) and (f; z), both of which show a global spectral gap. The center and width of this spectral gap largely agree with a simple analytical estimate from
). The numerically constructed magnetic field with absorbing beach is shown in Fig. 7. Figure 8 gives the surface plots of computed wave field in the spaces of (f; r) and (f; z), both of which show a global spectral gap. The center and width of this spectral gap largely agree with a simple analytical estimate from
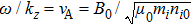 and ω± = ω0(1 ± ε/2),[5,7,8] which gives f = 188 ± 47 kHz.
and ω± = ω0(1 ± ε/2),[5,7,8] which gives f = 188 ± 47 kHz.
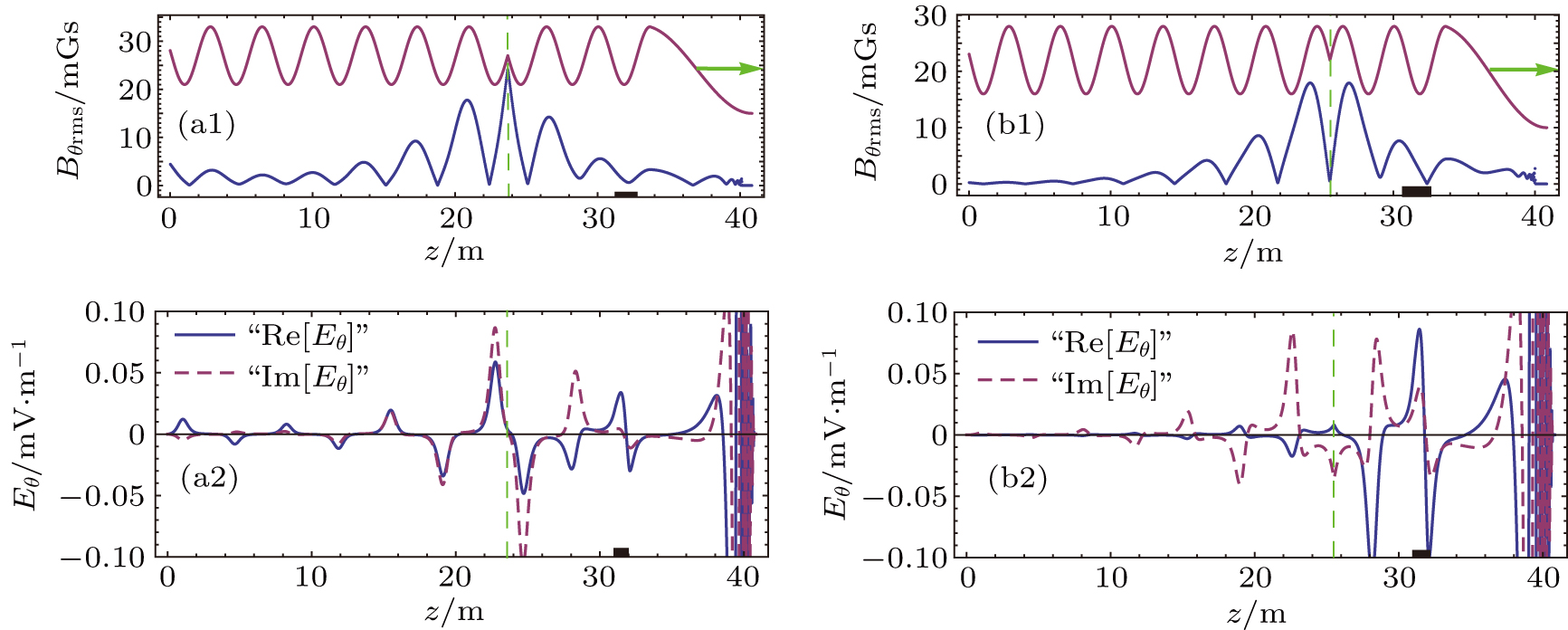
Following a similar strategy as used before,[7,8] two types of gap eigenmodes can be formed inside the spectral gap, namely odd-parity and even-parity for two types of defects, as shown by the surface plots in Fig. 9. Here the collisionality has been decreased by a factor of 10 to obtain sharp resonance peaks. The employed periodic static magnetic field with local defects are shown in Fig. 10(a1) and Fig. 10(b1), together with the axial profiles of peak gap eigenmodes. The parity is featured by the axial profile of Eθ across the defect location as illustrated in Fig. 10(a2) and Fig. 10(b2). It can be seen that the wave length of formed gap eigenmode is nearly twice the periodicity of external magnetic mirror, which is consistent with the Bragg’s law. Moreover, the eigenmode is a standing wave localized around the defect, same as observed previously.[7,8] The odd-parity and even-parity gap eigenmodes peaks at f = 140 kHz and f = 185 kHz, respectively, in the range of 50 kHz–300 kHz with the resolution of 5 kHz.
To implement these gap eigenmodes on the LAPD, there are three limitations considering the present experimental capability: field strength, plasma density and machine length. The maximum field strength is 0.3 T at present,[6] thus it may need super conducting magnets to become 6 times stronger, namely 1.8 T.[13] More input power or innovative ionization method is also required to enhance the plasma density from maximum 2 × 1019 m−3 now to 9.2 × 1019 m−3.[13,14] The length of mirror area could be doubled by setting up a reflecting endplate which turns back Alfvén waves to propagate again through magnetic mirror array. An alternative way is to reduce the periodicity of each mirror to be half, namely 3.63/2 m. The odd-parity and even-parity mode features correspond to boundary conditions of
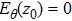 and
and
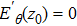 respectively,[7,8] and can be implemented by a conducting mesh and conducting ring in experiment, whose radial and axial slots are then required accordingly to prevent the formation of azimuthal current.[8] Hence, these limitations are solvable in experiment. The following section will be devoted to further removing these limitations by reducing the field strength, plasma density and the number of magnetic mirrors.
respectively,[7,8] and can be implemented by a conducting mesh and conducting ring in experiment, whose radial and axial slots are then required accordingly to prevent the formation of azimuthal current.[8] Hence, these limitations are solvable in experiment. The following section will be devoted to further removing these limitations by reducing the field strength, plasma density and the number of magnetic mirrors.
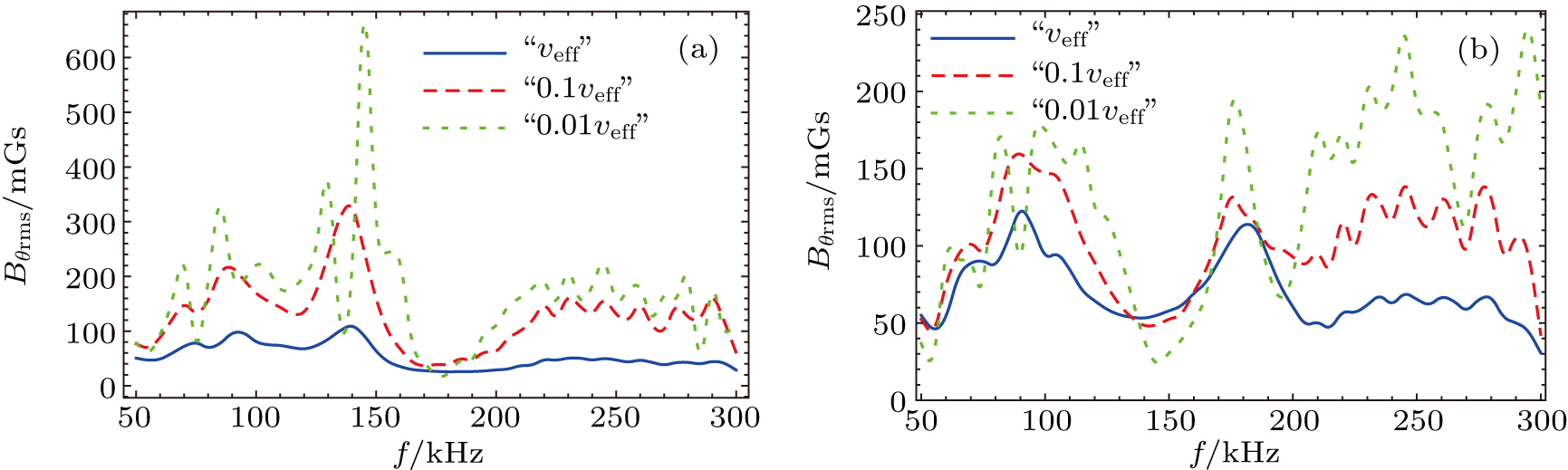
3.2. Low field strength and plasma densityThis section aims to guide the experimental implementation of gap eigenmode based on the realistic conditions of the LAPD. First, the field strength will be decreased to the present capability of the LAPD, and magnetic field of B0(z) = 0.2 + 0.1 cos[2π(z − 33.68)/3.63] (maximum 0.3 T) with absorbing beach is thereby employed. Second, the plasma density will be reduced to 2.56 × 1018 m−3 (less than 2 × 1019 m−3) to maintain the same phase velocity of Alfvén waves, allowing comparison with previous sections in the same frequency range. The computed gap eigenmodes are shown in Fig. 11, which peak at f = 140 kHz and f = 180 kHz for odd-parity and even-parity modes respectively. The employed configurations of defective magnetic field are the same to those shown in Fig. 10 except the level of strength which is 6 times less here. It can be seen that both the odd-parity and even-parity gap eigenmodes are clearly visible inside the spectral gap, although their decay lengths are much shorter than those shown in Fig. 9. This states that for the present conditions of LAPD, the gap eigenmode of SAW can be formed immediately once the mirror number is doubled. Moreover, the comparison between Fig. 9 and Fig. 11 implies that stronger magnetic field makes it easier for the experimental observation. Although these gap eigenmodes are still visible for original Coulomb collisions and electron Landau damping, the total effective collision frequency (νeff = νei + νe − Landau) has been multiplied by 0.1 for clear formation in Fig. 9 and Fig. 11. The effect of this collision frequency on gap eigenmode strength is shown in Fig. 12. As discussed in a previous study,[7] the resonant peak decreases and broadens for larger values of νeff, but it is still clearly visible even at the highest collision frequency.
3.3. Reduced number of magnetic mirrorsNow we shall remove the last limitation for immediate experiment on the LAPD by decreasing the number of magnetic mirrors. The even-parity gap eigenmode for original Coulomb collisions and electron Landau damping will be employed. The odd-parity gap eigenmode exhibits similar features and are thereby omitted. The constructed profiles of defective magnetic field with different numbers of mirrors are shown in Fig. 13(a) and the resulted variations of peak wave magnitude (rms) with frequency are shown in Fig. 13(b). These peak magnitudes are measured at r = 0.0371 m and axially 1.4548 m away from the defect location. It can be seen that the gap eigenmode is clearly formed even for the least number of magnetic mirrors, namely 4 on LAPD. The reduction of magnetic mirrors has negligible effect on the frequency and width of the gap eigenmode. The three-dimensional surface visualizations of this gap eigenmode for 4 magnetic mirrors are shown in both (f; z) and (f; r) spaces in Fig. 14. For left figures, the employed collisionality consists of original Coulomb collisions and electron Landau damping, whereas it is decreased by a factor of 10 for right figures as done in Fig. 9 and Fig. 11. Although the spectral gaps become less clear, compared with those in Fig. 11(b1) and Fig. 11(b2), the formed gap eigenmodes are still visible, especially in the radial direction. This strongly motivates the experimental implementation of this gap eigenmode on the LAPD.
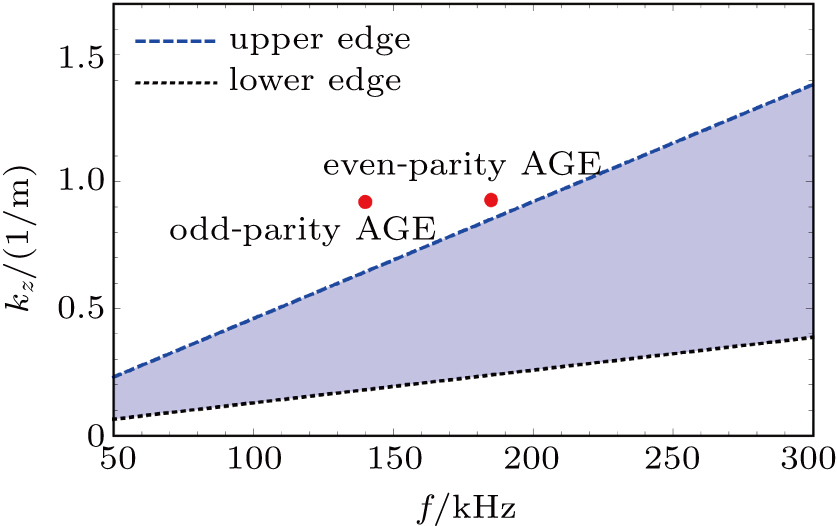
4. Discussion and conclusionTo check whether the gap eigenmode shown in Fig. 9 is shear Alfvén mode or compressional Alfvén mode, we run EMS for various driving frequencies for uniform static magnetic field and calculate the dominant axial wavenumber kz via Fourier decomposition. The computed dispersion curves at r = 0 m and r = 0.12 m are given in Fig. 15, together with their comparisons with analytical theory. We can see that numerical and analytical curves agree well (wiggles are caused by reflections from endplate and can be smoothed when the endplate is moved further away). Moreover, the considered frequency range 50 kHz–300 kHz is far below the ion cyclotron frequency fci = 4.57 MHz. Therefore, it is reasonable to claim that the formed gap eigenmode here belongs to shear Alfvén branch. To check whether the continuum damping resonance of Alfvén waves effects the gap eigenmode formation, we compute the continuum damping region which is enclosed by Alfvénic dispersion curves on plasma core and at plasma edge. Figure 16 illustrates the computed continuum damping region, which is enclosed by dispersion relations of kz = 2πf/vA on axis and at plasma edge respectively, and the locations of peak gap eigenmodes in Fig. 9. It is clear that both odd-parity (140 kHz) and even-parity (185 kHz) gap eigenmodes lay outside of the continuum damping region thereby are unaffected by continuum resonance.
In summary, to guide the experimental implementation of the gap eigenmode of SAWs on the LAPD, this work computes the gap eigenmode using exact parameters of the LAPD. We start from the reproduction of wave field for previous experiment and find that previously observed spectral gap is not global but an axially local result. By increasing the number of magnetic mirrors and static magnetic field strength, we obtain a clear and global spectral gap in both axial and radial directions. After introducing local defects, two types of gap eigenmodes are formed inside the spectral gap, namely odd-parity and even-parity. These gap eigenmodes are standing waves localized around the defects and have wavelength twice the periodicity of external magnetic mirror, which is consistent with Bragg’s law and previous studies.[7–9] These gap eigenmodes can be successfully formed even for the field strength, plasma density and number of magnetic mirrors that are achievable on the LAPD at its present status. This preliminary computation strongly motivates the experimental observation of the gap eigenmode of SAWs on the LAPD and other relevant linear plasma devices.