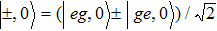† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11504272, 11774262, 11474003, and 11504003), the National Key Basic Research Special Foundation (Grant No. 2016YFA0302800), the Joint Fund of the National Natural Science Foundation of China (Grant No. U1330203), the Fund from the Shanghai Science and Technology Committee (STCSM) (Grant No. 18JC1410900), and the Natural Science Foundation of Anhui Province, China (Grant Nos. 1408085MA19 and 1608085ME102).
We theoretically study the collective decay of two atoms trapped in a single mode cavity and we describe the evolution of the population of Dicke states. We show that the collective decay property is strongly dependent on the phase of atomic radiation and the speeding up of collective decay can only be observed in a bad cavity regime. For in- or out-phase case, this occurs due to the quantum interference enhancement, no matter which atom is excited initially. For π/2 phase, the speeding up of collective decay takes place if the first atom is excited at the beginning. However, it disappears due to the quantum interference cancellation if the second atom is excited. Compared with the in-phase and out-phase cases, we also show that the speeding up of collective decay can be significantly enhanced in strong coupling regime for π/2 phase, although one atom is decoupled to the cavity in this condition. The study presented here is helpful to understand the physical mechanism of collective decay in cavity quantum electrodynamics and it provides a useful method to control the collective decay phenomenon via quantum interference effect.
Quantum interference effects are basic features of quantum mechanics, they are also the foundation of quantum optics. There are various interesting optical phenomena that are essentially based on quantum interference effects, for example: electromagnetically induced transparency,[1] lasing without inversion (LWI),[2,3] and refractive index enhancement without absorption.[4] In addition, quantum interference can lead to the modification of atomic spontaneous emission, such as, spontaneous emission enhancement in photonic crystals[5,6] and reduction even cancellation in three-level atoms.[7–9]
It is well-known that the spontaneous emission rate emitted by quantum emitters can be modified by inhomogeneity of the cavity environment in the Purcell effect.[10] Purcell also demonstrated that the spontaneous emission rate is not an intrinsic property of the emitter. Since then, great attention has been drawn on resonant systems to study the enhancement of the spontaneous emission decay rate, such as plasmonic waveguides,[11] photonic crystals,[6,12,13] nanocavities,[14,15] and nanoshells.[16] However, it is hard to enhance the total (collective) emission in an ensemble of quantum emitters system due to the severe condition of the emitters’ accurate location as well as the neighboring large and homogeneous electric field distributions in resonating systems.
Collective emission or decay occurs in an ensemble of quantum emitters system where the emitters are coupled to a lossy cavity[17,18] or close to each other.[19,20] Collective decay is of fundamental interest in quantum optics and has attracted tremendous attention[21] since the seminal work by Dicke,[22] especially relating to the phenomenon to super-radiance.[19,23–26] The phenomenon can be attributed to the constructive quantum interference between emitted waves and has been widely investigated in various photonic environments.[27–33] Through coherent control of collective decay, the super-radiant states can be converted into subradiant ones and vice versa in an extended atomic ensemble.[34] Chen et al. proposed a scheme to realize entanglement swapping via collective decay, which is a procedure to create entanglement between two qubits.[35] Agarwal et al. showed determinstic generation of Werner states of the collective decay dynamics of a pair of neutral atoms coupled to a leaky cavity and strong coherent drive.[36] Wang et al. also presented a simple scheme to effectively generate maximal pure-state entanglement between non-interacting atoms through purely collective decay.[37] Despite all of these research achievements, the nature or physical mechanism of collective decay is, even today, not well understood.
In this paper, we have carefully studied the dynamics of atomic collective decay in cavity quantum electrodynamics. We assume that two atoms are trapped in a single mode cavity with different positions and that one of them is initially excited by a single photon. It is found that the decay properties of the Dicke states are strongly dependent on the phase between two atoms. We show that the speeding up of collective decay can only be observed in the bad cavity regime due to the quantum interference effect. In the case of in-phase or out-phase radiation, the decay rate of the Dicke state is much faster than that of the single atom, which is recognized as a witness of the single photon super-radiance.[38] Here, it should be emphasized that the obtained single photon super-radiance is referred to the collective decay enhancement of two atoms trapped in a cavity via single photon excitation comparing with the spontaneous decay of one atom in vacuum. We also show that the properties of the collective radiation change significantly if the atoms feel different coupling strengths to the cavity. For example, in the case of π/2 phase, the speeding up of the collective decay can be observed when the first atom is excited initially, while it disappears if the second atom is excited at the beginning. Particularly, in the case of π/2 phase, the speeding up of the collective decay can be significantly enhanced by increasing the coupling strength. The results presented in this work are helpful for understanding the nature of the collective decay phenomenon in the cavity and can be implemented in other systems.
To begin with, we consider that two two-level atoms with the same resonant transition frequency ωA are weakly coupled to a single mode cavity with frequency ωC [see Fig.
The dynamical evolution of this atom–cavity coupled system can be well described by the Jaynes–Cummings Hamiltonian in the frame rotating with the cavity frequency,[39,40] i.e.,
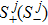
In the normalized unit with ħ = 1, the evolution of the density matrix ρ of this system, including all the dephasing terms, is given by
In general, equation (

Considering the lowest three states of this simplified system for single photon excitation, i.e., |1〉 = |gg〉, |2〉 = |eg〉, and |3〉 = |ge〉, we can obtain a set of equations from Eq. (


If one assumes 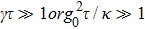
Then, by inserting the above equation into Eqs. (



Equations (
The physical mechanism can be understood by rewriting the Hamiltonian by using the collective states 


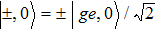
To verify this analysis, we numerically solve Eqs. (
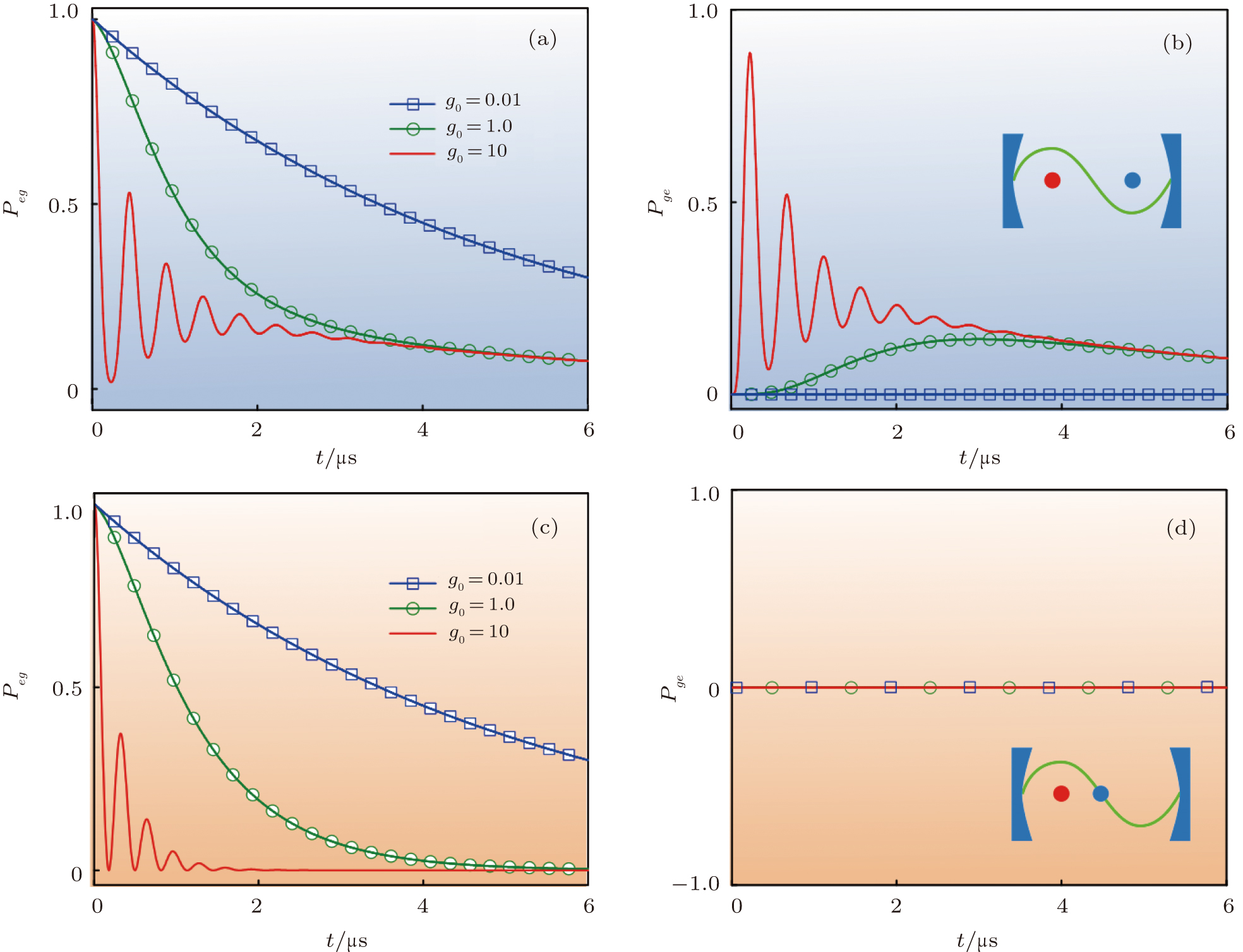
 | Fig. 2. (color online) The populations in states |eg〉 [panel (a)] and |ge〉 [panel (b)] with initial condition Peg(0) = 0 and Pge(0) = 1. The system parameters are chosen as g0 = 1, κ = 3, and ΔA = 0. |
The initial conditions are chosen as Peg(0) = 0 and Pge(0) = 1. Here, we choose the system parameters as g0 = 1, κ = 3, and ΔA = 0. If one chooses ϕz = π/2 where the population in state |ge〉 exponentially decays at the rate of 2γ [see panel (b) of Fig.
Next, we will study the collective decay effects if the two atoms are initially prepared in state |eg〉 (i.e., Peg(0) = 1 and Pge(0) = 0). Using the same method, the solutions of Eqs. (
The solutions are similar to those given in Eqs. (
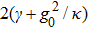


By once more numerically solving Eqs. (
Now, we consider the case of g0 ≫ κ,γ, i.e., the strong coupling regime. Since the back reaction becomes important in this case, equation (
As shown in Fig. 
In the case of ϕz = π/2, we show that the decay rate of state Pge is the same as that for the single atom, and Peg = 0 no matter how strong the coupling strength is [see panels (c) and (d) in Fig.
In Fig. 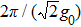
We have shown that the behavior of the atomic collective decay significantly changes with the phase between the two atoms trapped in a high damping cavity. This arises from the quantum interference between Dicke states. We found that in the case of in-phase or out-phase radiation, the speeding up of the collective decay occurs due to the constructive quantum interference, no matter which atom is excited initially. In the case of π/2 phase, the speeding up of the collective decay can also be observed if the first atom is excited initially. Although in this case the second atom does not couple to the cavity, the constructive interference still exists and results in an enhanced decay rate of the Dicke state. However, the speeding up of the collective decay disappears due to the destructive quantum interference if the second atom is excited at the beginning. In addition, the speeding up of the collective decay can be significantly enhanced in the strong coupling regime for the π/2 phase. The study presented here is helpful to understand the nature of the speeding up of the collective decay in cavity quantum electrodynamics, and provide an effective method to control the collective decay via quantum interference effect.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |