† Corresponding author. E-mail:
Project supported by the Key Science and Technology Research Project of Henan Province, China (Grant Nos. 162102210164 and 1721023100107) and the Natural Science Foundation of Henan Educational Committee, China (Grant No. 17A140002).
We propose and numerically demonstrate a tunable plasmon-induced transparency (PIT) phenomenon based on asymmetric H-shaped graphene metamaterials. The tunable PIT effect is realized through varying the applied polarization angles rather than changing the structure geometry. By simply adjusting the polarization angle, the transmission spectra can be controlled between the switch-on state and switch-off state. The physical mechanism of the induced transparency is revealed from magnetic dipole inductive coupling and phase coupling. Importantly, by varying the Fermi energy of the graphene or the refractive index of the substrate, the resonant position of the PIT can be dynamically controlled and the maximum modulation depths can reach up to 60.7%. The sensitivity (nm/RIU) of the graphene structure, which is the shift of resonance wavelength per unit change of refractive index, is 5619.56 nm/RIU. Moreover, we also extend our research to the x-axis symmetric H-shaped structure, and the tunable PIT transmission window can also be realized. The physical mechanism of the induced transparency is revealed from the electric dipole hybridization coupling. Our designed H-shaped graphene-based structures is a promising candidate for compact elements such as tunable sensors, switches and slow-light devices.
Electromagnetically induced transparency (EIT) is a quantum interference phenomenon in the weak electromagnetic field under the effect of a strong driving electromagnetic field in the atomic system.[1–3] This results in a narrow window in the transmission spectrum. The plasmon-induced transparency (PIT), an EIT-like effect, has attracted attention due to its significant advantages and wide practical applications,[4,5] such as in sensors,[6–9] optical storage,[10–12] optical switches, and so on.[13–16] However, for metal metamaterials, once the PIT devices have been fabricated, the transmission window is very difficult to tune except by accurately changing the geometry of structures, which limits the performance and repeatability of designated PIT sample. Recently, graphene has been introduced into the design of PIT devices due to its unique optical and electrical properties.[17–19] It exhibits the characteristic of the flexible tunability, the extreme field confinement and low propagation loss, especially the gate-voltage-dependent feature that the Fermi energy (EF) of graphene can be tuned dynamically by using the external electrostatic gating.[20,21]
Hence, graphene can be considered as a new class of active plasmonic material for application in photonic devices. Fu et al. proposed a novel disk-strip hybrid graphene nanostructure to achieve PIT resonance that has a large positive group delay in the vicinity of the resonant transparency window.[22] They also presented two parallel graphene nanostrips that can be used as a localized surface plasmon resonance sensor in the mid-infrared region.[23] Luo et al. achieved PIT effects based on the strong coupling between localized and propagating plasmonic mode in layered graphene ribbon-grating and continuous sheet systems.[24] Zhang et al. have studied the tunable PIT with graphene-array metasurface.[25] Compared with this research, we have systematically investigated the tunable PIT effect through varying the polarization angle and the fermi energy, which makes manipulating of the PIT system more effective and contactless. We also compared the application of the designed structure in sensitivity with those of other structures.
In this paper, we propose the self-asymmetric H-shaped graphene metamaterial to achieve the PIT effect. Interestingly, the modulation of the PIT transparency window can be achieved by varying the polarization angles rather than changing the structure geometry parameters. Owing to the unique properties of graphene, the resonant transparency window can be dynamically tuned by the Fermi energy. Moreover, the sensitivity of 5619.26 nm/RIU is achieved in the proposed structure based on the sensitivity measurements with different dielectric substrates. The physical mechanism of the induced transparency is revealed with magnetic dipole inductive coupling and phase coupling. We also extend our research to the x-axis symmetric H-shaped graphene metamaterial, and the PIT effect can also be tuned through varying the polarization angle and the fermi energy. However, the underlying mechanism is the detuning of two bright modes.
The designed asymmetric H-shaped graphene structure with a 7×7 cell array is shown in Fig.
In the simulations, graphene is modelled as a conductive surface.[17,26,27] The transition boundary condition is used for graphene and its thickness is set to be 1 nm. The conductivity of graphene can be derived in the random-phase approximation (RPA) in the local limit, and expressed as[19,28,29]

Electron-beam lithography and isotropic plasma etching are used to pattern graphene nanostructures.[33] To obtain the graphene metamaterial structures, a uniform single layer of graphene needs to be prepared at first. It can be obtained through mechanically extracted from bulk graphite crystals,[34] thermal decomposition of Sic,[35] and chemical vapor deposition method.[36] The most common method is chemical vapor precipitation, which produces a graphene layer with high conductivity and field-effect mobility. For the preparation of graphene nanostructures, electron beam lithography is very popular because of its high resolution; usually reaching up to 3 nm to 8 nm.[37] Recently, anisotropic etching has been proposed as a key technique for controllable graphene edge fabrication with atomic precision. Yang et al. reported a dry, anisotropic etching method of preparing the graphite and graphene. They are able to control the etching from the edges by tuning etching parameters such as plasma intensity, temperature, and duration.[38] Similarly, the asymmetric H-shaped graphene can be prepared through the following steps: first, a graphene layer synthesized with chemical vapor deposition is transferred to the substrate. Secondly, the H-shaped graphene array is completed by electron beam lithography. Then, the ion gel can be utilized as the top gate, while the bottom of substrate is used as the back gate. Finally, the carrier density in graphene can be changed by adjusting the voltage, and then the conductivity of graphene can be dynamically adjusted.
Figures
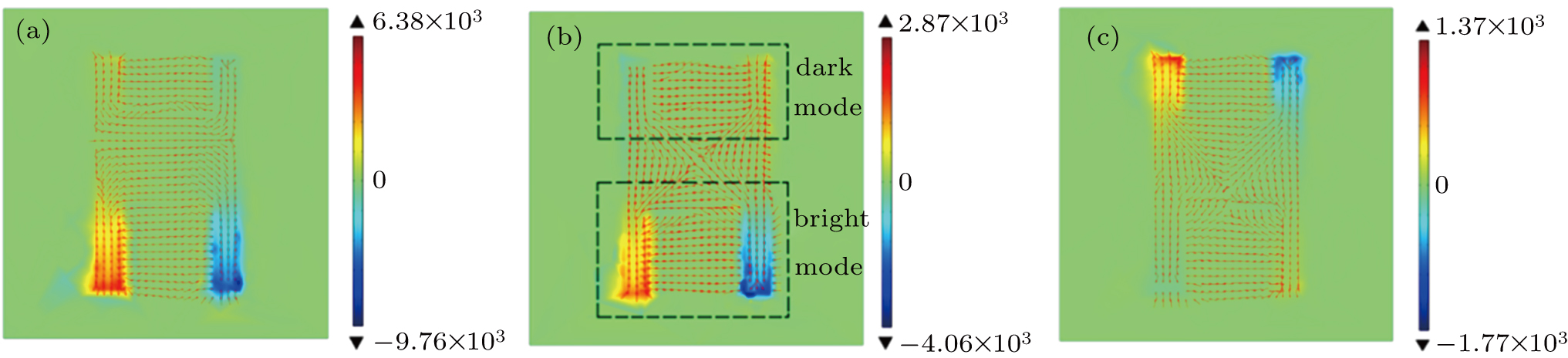
To fully dig out the origin of such a PIT phenomenon, the normalized electric field distribution and normalized surface current distribution (in arrows) are given in Figs.
To better reveal the mechanism of PIT resonance in our proposed structure, we investigate the electric field and normalized surface current distributions at 0° polarization angle. The results are shown in Fig.
 | Fig. 4. (color online) Surface currents excited by magnetic-dipole coupling with the propagation waves. |
In addition, it should be pointed out that the optical properties of graphene can be substantially modified via doping or gating since the conductivity of graphene depends strongly on Fermi energy. We can dynamically tune the transparency window over a broad wavelength range by controlling the Fermi energy levels of graphene. The results are shown in Fig.
 | Fig. 5. (color online) (a) Transmission spectra of graphene based PIT structure under normal incidence at different values of EF, and (b) relationship of the resonant PIT peak with Fermi energy EF. |
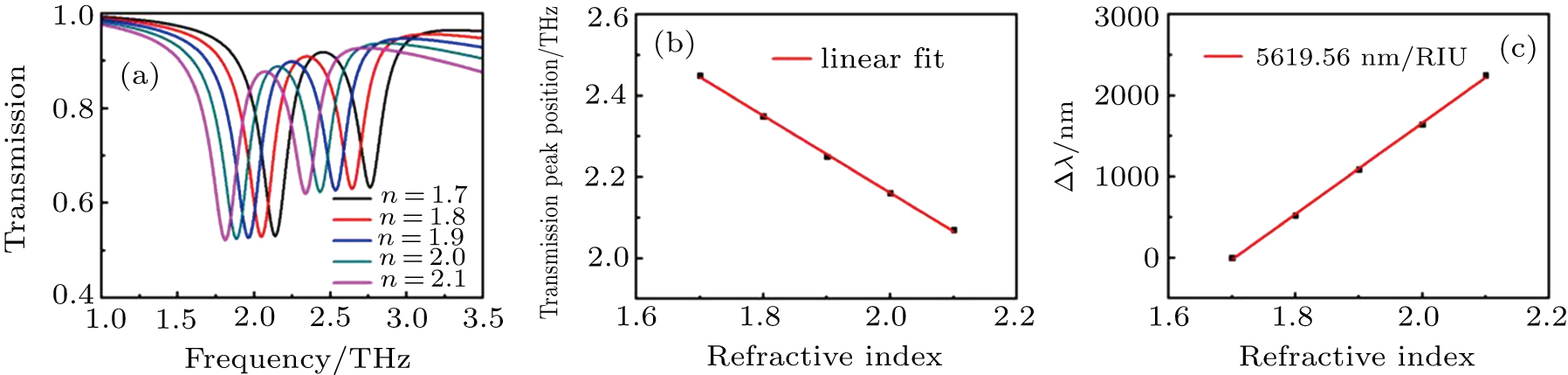
To explore the sensing ability of our proposed structure, figure
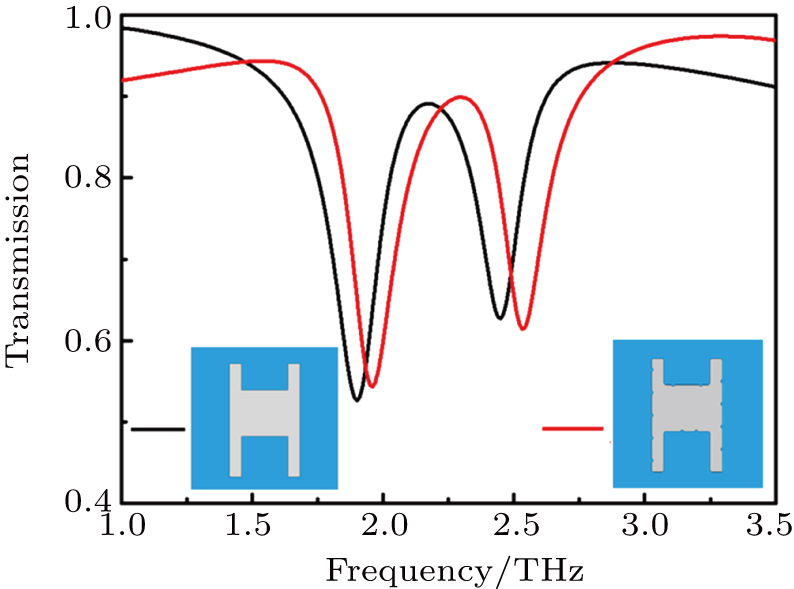
Moreover, we also investigate the PIT effect of the x axial symmetric H-shaped structure at different values of polarization angles θ, and the results are shown in Fig.
Now we come to investigate the dependence of the absorption spectrum on Fermi energy for the x axial symmetric H-shaped structure. The contour of Fermi energy ranging from 0.5 eV to 0.8 eV versus frequency of the designed structure is plotted in Fig.
 | Fig. 8. (color online) Contour of Fermi energy versus frequency of x-axial symmetric H-shaped structure. |
Graphene is an attractive 2D carbon material.[41] The carbon-to-carbon in-plane bond in graphene is very strong, which makes graphene sheets quite robust. However, carbon atom vacancies with respect to what would be a perfect armchair around the edge appears difficult to avoid.[42–44] We calculate the transmission spectrum and electric field distribution of the asymmetric H-shaped graphene structure with rough edges. The transmission spectrum of rough edge structure is simulated and compared with that of smooth edge structure in Fig.
In this work, we theoretically investigate the dynamically controllable PIT effect with two kinds of asymmetric H-shaped graphene resonators by varying polarization angles rather than changing the structure parameters. The transition from the switch-on state (PIT mode) to switch-off state (dipole mode) is theoretically demonstrated by simply adjusting the polarization angle. Importantly, the destructive interference between a dark mode and a bright mode is employed to analyze the transmission mechanism. The PIT resonance frequency can be dynamically tuned by adjusting the Fermi energy of the graphene, instead of re-fabricating the structures. The tunable PIT effect of the x axis symmetric H-shaped structure by the polarization angle is also investigated. The physical mechanism of the induced transparency is revealed from the electric dipole hybridization coupling. Moreover, our proposed asymmetric H-shaped graphene structures with rough edges can also embody the PIT effect. Based on the observed phenomenon, our designed H-shaped structures could offer new opportunities for applications in optical filter, optical sensors, and switches.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] |