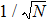† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant Nos. 2016YFF0200103 and 2016YFF0200200) and the Fundamental Research Funds for National Institute of Metrology, China (Grant No. 22-AKY1608).
The scale factor of a superconducting gravimeter (SG) is usually calibrated by using simultaneous and co-located gravity measurements with the FG5-type absolute gravimeter (AG). In this paper, another new kind of absolute gravimeter-cold atom gravimeter (CAG) is first reported to calibrate the SG. Five-day side-by-side gravity measurements have been carried out by using our CAG (NIM-AGRb-1) to calibrate the SG (iGrav-012) located at Changping Campus of the National Institute of Metrology (NIM) of China. A weighted least-squares method is applied to determine the scale factor and the result is given as (−928.01 ± 0.73) nm⋅s−2⋅V−1 with a precision of 0.79‰. We have demonstrated that a calibration precision of 1‰ level can be achieved after 3 days of parallel observations at spring tide. The obtained calibration results are then compared with the previous calibration by FG5X-249, which shows that the calibration precision obtained by using NIM-AGRb-1 was slightly higher than FG5X-249 with the same time interval. The factors affecting the calibration precision are analyzed in the calibrations by means of different AGs. Finally, several calibration experiments for SG iGrav-012 are discussed. The final scale factor is estimated as (−927.58 ± 0.36) nm⋅s−2⋅V−1 with an accuracy of 0.39‰. Our main results demonstrate that the CAGs can be used for high-precision calibrations of SGs.
The superconducting gravimeter (SG) is the most precise relative gravimeter for the gravity measurement. The long-term gravity observations are widely used to investigate different kinds of geophysical processes, such as Earth tide, core and wobble modes, polar motion, ocean and atmospheric loading, sea level changes, the hydrological model, and theoretical Earth tide models.[1–4] The output of SG is a voltage signal, which controls the current in a superconducting feedback coil to keep the balance of a superconducting niobium sphere between the gravity and electromagnetic force. A scale factor is required to convert the voltage into gravity variations, which needs to be accurately calibrated for those applications. The calibration precision of 1‰ is demanded for most of the applications of SGs. For example, the calibration precision should be better than 1‰ for constraining the Earth tide model or oceanic tide model.[5] In 2017, the 10th International Comparison of Absolute Gravimeters (ICAG-2017) was held at Changping Campus of the National Institute of Metrology (NIM) China.[6] The accurate calibration of the SG is of great significance for the traceability of absolute gravity data at the comparison site.
There are several methods for SG calibration. For example, a direct method employs devices to generate controlled acceleration changes to the instrument, which can be done either by moving an external known mass[7] or by moving the instrument using a platform.[8] This method requires some special techniques to manage heavy reference masses, which is difficult to achieve for every SG station. A precision of 10−4 is achieved by using this method. Another method monitors the tides for a long period (2–3 years) and then use a well-known tidal amplitude for calibration.[9] This method works well but is time-consuming for a long-time data series.
The most widely used method for calibration is to apply simultaneous and co-located measurements of gravity changes with a reference gravimeter, especially an absolute gravimeter (AG).[10–13] The scale factor of the SG is determined by applying a least-squares (LS) linear fit method to the parallel observations of SG and AG data. As can be known from the theoretical estimation, the factors that limit the calibration precision are the precision of the absolute gravimeter, the number of the observation data and the amplitude of gravity changes during the calibration. Imanishi et al. used the FG5-210 to calibrate the SG T011 with a final precision of 0.39‰.[14] Francis et al. realized simultaneous observations of the FG5-202 and SG C024 with a calibration precision of better than 1‰.[15] Camp et al. provided an optimized strategy by comparison with an AG to achieve a robust calibration estimation at 1‰ level.[16] These works demonstrate that a precision of 1‰ can be obtained from the calibration by using an AG.
FG5-type absolute gravimeters are the most popular instruments used for the calibration of the SGs. In this paper, we use another kind of absolute gravimeter — the cold atom gravimeter (CAG) — to calibrate the SG iGrav-012 located at Changping Campus of NIM. As far as we know, this is the first study on the calibration of SGs by using a CAG. Nowadays, CAGs have become a promising tool for ultrahigh-precision measurements of absolute gravity, which employ cold atoms as inertial sensor.[17–20] There are two advantages in the SG calibration by using the CAG. First, the CAG has a low measurement noise, as well as high sampling rate, which predicts a higher calibration precision. For example, the best noise estimation of 42 nm·s−2⋅Hz−1/2 with a sampling rate of 1 s has been reported in Ref. [21]. In contrast, the instrumental noises of FG5 absolute gravimeters are usually between 300 nm·s−2⋅Hz−1/2 and 680 nm·s−2⋅Hz−1/2 with a sampling of 100 to 200 drops per hour.[22] Second, there is no mechanical friction between atoms and the vacuum chamber during the drops of the test mass in a CAG system. The mechanical dissipation in the FG5-type AGs would reduce the lifetime of the instrument. Therefore, the CAGs are more suitable for continuous and long-term absolute gravity measurements. This is quite advantageous for high precision calibration of SGs.
A mobile CAG based on light-pulse atom interferometer has been built by NIM, which is named NIM-AGRb-1. The noise estimation of NIM-AGRb-1 is reported as 440 nm·s−2⋅Hz−1/2, which is a little bit better than the 560 nm·s−2⋅Hz−1/2 of the FG5X-249.[23] In this study, a calibration experiment on the SG iGrav-012 was performed by using NIM-AGRb-1.The calibration result was then compared with the previous result calibrated by FG5X-249. Based on this, the factors affecting the calibration precision were then compared between those two kinds of AGs. Finally, several calibration experiments on SG iGrav-012 by different kinds of AGs were analyzed and discussed.
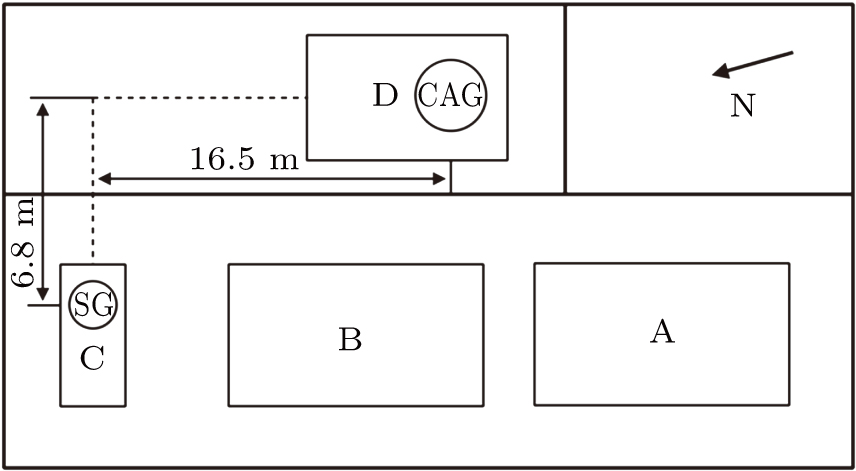
The compact SG iGrav-012 from GWR company was installed at Changping Campus of the NIM in 2014. The coordinates of the instrument are 40.245° N, 116.225° E. It is now operated at the comparison site located at the foot of a hill in the north of Changping District, which is an isolated rural area. The comparison site at NIM consists of three isolated piers. They are designed to separate from the main building structures to avoid transmitting the vibration of the main building structures to the pillars. The relative position is shown in Fig.
Based on the theory of variance evaluation, it is known that the precision of the calibration factor can be optimized by selecting a proper time period when gravimetric tide reaches its extrema.[24] Taking this factor into account, the co-located observations of SG and CAG were carried out for a period of five days from 4th to 8th October 2017. The time interval for each drop is 1 s. To eliminate the disturbance of high-frequency noise from earthquakes and other factors, we make an average of every 60 drops as a data point, corresponding to a sample interval of 1 minute. Table
| Table 1. Absolute gravity measurement of parallel observations at NIM. . |
After the acquisition of absolute gravity data, the performance of CAG was first evaluated. The residuals of absolute gravity measurement were obtained by subtracting the theoretical Earth tide and the effect of the atmospheric pressure changes from the raw data, as shown in Fig.
 | Fig. 3. (color online) Co-located observations of the SG (red line) and the CAG (black dot) in Changping Campus of NIM. |
The original SG data consists of continuous outputs of voltage signal with one sample each second. First, we selected the SG data at times corresponding to the observations of CAG. Here, the time lag of 10.374 s caused by the analog filter was taken into consideration. We then removed the spikes and abnormal observations due to earthquakes. These abnormal data are not suitable to be processed by a filter, so we remove them before filtering. The possible signal shift because of a sudden break, if any, should be handled in this procedure. Finally, a low-pass digital filter was applied to the data, decimating 1-s SG data to 1 minute. This filter was used to eliminate microseismic noise and other disturbances. The processed SG data is plotted together with the CAG observations in Fig.
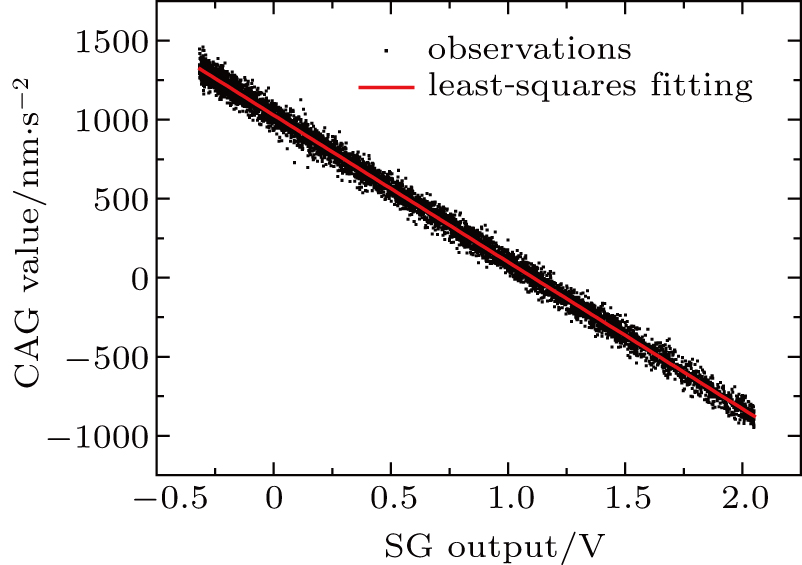
A least-squares (LS) linear fit method is applied to the parallel observations of SG and CAG data. According to the previous studies,[26] the root mean square (RMS) amplitude of the SG instrumental noise is at 1 nm·s−2 level. This is lower than the CAG white noise by two orders of magnitude, the RMS amplitude of which is 350 nm·s−2 when taking one drop every one second. Therefore, it is assumed that instrument noise only exists in the CAG data in the fitting process. The model of LS fit can be expressed as
In most cases, the measurement errors are not homogeneous throughout the observation period; for example, several error sources from laser problems or environmental noise may contribute to the measurement error coming from the drop scattering. Therefore, the weighting function is necessary to be applied in the LS fit procedure. First, the CAG data is divided into different sets of every 60 data points with a period of an hour. Next, the standard deviation of each set σn is derived from a statistical processing among which outliers are discarded with a threshold value of three times the standard deviation. Then, the weighting factor can be expressed as 
Assuming that the measurement error of yn follows a normal distribution, we aim to find the a, b, and c values that minimize the weighted sum of squared residuals Sw,
After the data have been processed, the number of the final remaining data series is 6803. The utilization of the data is 99.5%. The result of the LS fitting is shown in Fig.
The residuals of the LS fitting are shown in Fig.
The drift effect of the CAG observations is estimated by comparison with the result obtained by zero drift assumption in the fitting procedure. The calibration factor for the zero drift model is (−928.58 ± 0.73) nm·s−2.V−1 which deviates 0.6‰ from the results of the linear drift model. Furthermore, the result of the non-weighted least-squares fitting is also calculated and the value is (−928.07 ± 0.74) nm·s−2.V−1. The difference between the weighted and non-weighted method is less than 0.1‰ and the RMS errors of the two calibration factors are almost the same. The results indicate the measurement errors of the CAG caused by environmental noise and other factors are stable throughout the observation period.
In the calibration experiment, the precision of the scale factor depends on the length of the data series. To estimate how many days of the absolute gravity measurements that we need to achieve a precision of 1‰ required in our studies, the estimate of the scale factor as a function of the observation time has been investigated. The results are plotted in Fig. 
The calibration precision by NIM-AGRb-1 is also compared with the previous calibration by FG5X-249 (Fig.
For a complete comparison of calibration by absolute gravimeters with different sample rates and measurement errors, the important factors affecting the precision of calibration are estimated as follows. Assuming that the errors of the AG measurements are uniform throughout the experiment, the estimation error on the calibration factor σa determined by the least-squares fitting is given by[11]

The noise estimate of the FG5-type gravimeter is specified to be 50 nm⋅s−2 for a single drop at a quiet site. Assuming that it has a high repetition rate of one drop per 5 s, this means a sensitivity of 112 nm·s−2⋅Hz−1/2 can be achieved. However, higher duty cycles will reduce the lifetime of the instrument, especially in the case of continuous operation for a long time which is required in the calibration experiments. Therefore, the preferred sampling rate of the FG5 is one drop per 15 s, corresponding to a sensitivity of 194 nm·s−2⋅Hz−1/2 for continuous measurements. The CAG has achieved a sensitivity of as good as 42 nm·s−2⋅Hz−1/2 with a sampling rate of one shot per second, which has been the best reported value in the literature.[21] The calibration precision of 1‰ can be reached after 1.2 h by measuring at tide spring tides from the calculation on Eq. (
Since the SG iGrav-012 has been operating at NIM, several calibration experiments have been performed using different absolute gravimeters (FG5X and CAG).[31] All of the results are shown in Fig.
| Table 2. Calibration experiments of the SG iGrav-012 by using different absolute gravimeters. . |
The superconducting gravimeter (iGrav-012) at NIM has for the first time been evaluated by co-located absolute gravity measurements with cold atom gravimeter (NIM-AGRb-1). The calibration factor is determined by a weighted least-squares method and the result is given as (−928.01 ± 0.73) nm⋅s−2⋅V−1 with a precision of 0.79‰. We demonstrated that a calibration precision of 1‰ can be achieved by parallel gravity observations at spring tide for 3 days. The result was compared with the previous calibration by FG5X-249, and we found that the precision was slightly higher than the calibration result by FG5X-249 with the same time interval. The results were also verified by the theoretical estimation. A comparison of the calibrations using two AGs indicated that the calibration process by using CAG will be faster due to its high sensitivity and sample rate. Finally, several calibration experiments on SG iGrav-012 by different kinds of AGs are presented and discussed. A weighted average of all the experiments is calculated and the final result is (−927.58 ± 0.36) nm⋅s−2⋅V−1 with an accuracy of 0.39‰. Furthermore, the consistency of the calibration results demonstrates that the scale factor is stable, even if it was moved during this period.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] |