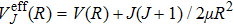† Corresponding author. E-mail:
Project supported by the Natural Science Foundation of Heilongjiang Province of China (Grant No. A2015011) and the Scientific Research Plan Projects of Heilongjiang Educational Department, China (Grant No. 135209258).
The potential energy curves of X1Σ+, A1Σ+, C1Σ+, and B1Π are calculated with high-level MRDCI method, and the calculated spectroscopic constants of those states are in good agreement with most recent experimental data. On the basis of high precision PECs, the radiative processes of H+ + Be collisions are studied by using the fully quantum, optical potential and semiclassical methods in the energy ranges of 10−8 eV/u–0.1 eV/u, and the radiative decay, the radiative charge transfer, and the radiative association cross-sections are computed. It is found that the radiative association process is dominant in the energy region of 10−8 eV/u–0.02 eV/u, while radiative charge transfer becomes important at higher energies. Rich resonance structures are present in the radiative association and charge transfer cross-sections in the whole energy region considered, which result from the interaction between the quasi-bound rovibrational (J, v) states in the entrance channel with the final continuum state. Significant isotope effects have been found in the radiative decay processes of H+ + Be collisions.
As a rare light element, Beryllium is the lightest stable nuclide not synthesized in the Big Bang and it has been used as probe as formation of the early universe, Galactic evolution and stellar structure together with Li and B,[1–4] which are regarded as a pure product of cosmic-ray (CR) spallation nucleosynthesis, are produced only by the cannonade of 13C and 16O by protons and α -particles. The abundances of these light elements and the corresponding ratio supplies some meaningful information on the affection of a planetary companion in the formation and evolution of stars.[5–10] For fusion science, beryllium is treated as a primary wall material and hydrogen is treated as the main plasma constituent, hence, studies of the collision processes between beryllium and hydrogen are of great interest.[1] Since 2011, the JET experiment has been carried out through an ITER-like wall that is constituted of beryllium and tungsten. In a plasma environment, beryllium erodes very easily because of chemical and physical sputtering, which discharge BeH2, BeH Be, and Be+ into the environment. Therefore, in the edge and divertor region of fusion plasma devices, a large variety of atomic and molecular collision processes need to be taken into account in modeling and interpreting spectroscopic diagnostics.
As the simplest beryllium hydride, the electronic structures of BeH and BeH+ have been intensively investigated by a number of research groups. A great number of methods have been constructed and used to calculate accurate potential energy curves (PECs) and spectroscopic constants. Colin et al. determined the Rydbcrg–Klein–Rees (RKR) potential energy curves of low-lying states (X2Σ+, C2Σ+, and A2Π) of BeH via spectroscopy analysis.[11,12] Later, the spectroscopic constant of X2Σ+ were evaluated by Colin et al. using high resolution infrared emission spectra of BeH.[13] Le Roy et al.[14] determined a ‘spectroscopic’ PEC of BeH through extracting the previously available experimental results of Colin et al. A precise ground-state PEC of BeH was recently obtained by Koput[15] utilizing a high-level ab initio method. Pitarch et al.[16] used a full configuration interaction method to compute the PECs and dipole moment curves of the low-lying states of BeH, and the avoided crossing between the electronic states of the same symmetry are discussed. Pitarch et al.[17] also used the same method to calculate vertical excitation energies, transition dipole, quadrupole moments, and oscillator strengths, and the transition properties were illuminated. In 1982, the PECs and spectroscopic constants for the X1Σ+ and A1Σ+ were computed by Ornellas et al. using the configuration interaction method.[18] Subsequently, Ornellas et al. systematically investigated[19–22] of the PECs, dipole moment functions, transition dipole moment functions and radiative transition probabilities of rovibrational states of BeH+. Recently, Bubin and Adamowicz[23] carried out Non–Born–Oppenheimer computations to obtain the ionization energy of BeH and dissociation energies of BeH/BeH+. Farjallah et al.[24] used the high-level quantum chemistry method, combining pseudo-potential to calculate the low-lying 44 electronic states of BeH+.
Some studies have recently been reported for collision processes of Be+–H and H+–Be. Errea et al.[25] investigated the total cross-sections of excitation and charge transfer processes in Be+–H or H+–Be collisions in the energy range of 0.2 keV/u–25 keV/u by employing the semiclassical molecular orbital close-coupling approach (SMOCC). Krstić and Schultz calculated the elastic differential and integral cross-sections, momentum transfer and viscosity cross-sections in Be+–H and H+–Be collision processes by utilizing the quantum-mechanically approach and the classical trajectory Monte Carlo (CTMC)[26] approach. More recently, Liu et al. studied the elastic, momentum transfer and projectile excitation cross-sections in Be+–H via the multichannel quantal molecular orbital close-coupling computations.[27] Compared with theoretical investigations, there are relatively few experimental work owing to the fact that BeH and BeH+ are extremely poisonous. Vibration-rotation spectra of BeH+ were investigated by different research groups.[13,28,29]
In this work, we conduct an extensive investigation on the radiative decay of H+(D+, T+)–Be(2 s2) collision processes in the energy range of 10−8 eV–10−1 eV, including the radiative charge transfer:
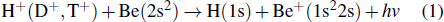 |
 |
In this work, the MRDCI procedure[30,31] is utilized to compute the PECs of the lowest three 1Σ+ and the lowest 1Π electronic state of BeH+ molecular ion. All of the inner shell and valence shell electrons of BeH+ molecular ion are considered in the MRDCI computations. The correlation consistent quadruple zeta Gaussian-type all-electron cc-pVQZ basis sets[33] are applied to describe beryllium and hydrogen atoms in the above calculations. In addition, the (3s, 3p, 3d) diffuse functions are included for the well-described Rydberg states. In the internuclear distances range of 1.5a0–100a0, the threshold for electronic configuration composition of BeH+ is chosen as 10−8 Hartree. With the aid of the Winger–Witmer principle, the corresponding relationship between electronic states and dissociation limits are presented as:
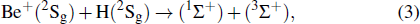 |
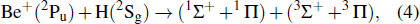 |
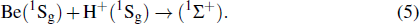 |
The calculated wave functions are then used to determine the dipole transition moments Di,j(R) required in scattering calculations:
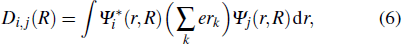 |
In this paper, the fully quantum-mechanical method has been applied for the treatment of the two radiative decay processes, radiative charge transfer and radiative association processes. In addition, both optical-potential and semiclassical methods have been adopted to study the radiative decay process for comparison. We will outline these methods in the following discussion.
The total emission cross-section in the collision process is defined by the sum of two contributions from radiative charge transfer and radiative association processes. In this work, we apply the fully quantum-mechanical method to compute the radiative charge transfer cross-section[9,10] and radiative association cross-section.[15,17] Now, we will give a brief account of the method. The radiative charge transfer cross-section is formulated as
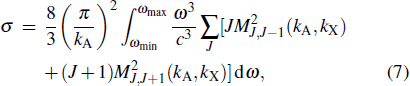 |
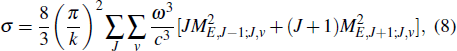 |

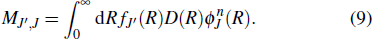 |
The entrance and exit wave function are obtained by solving the homogeneous radial equations
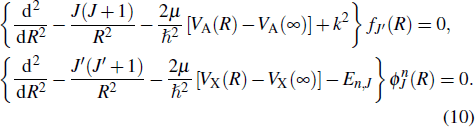 |
Here μ is the reduced mass, VA (R)and VX (R) are the PEC of the entrance and exit states, here En,J = E + ΔE − ħω, E is the relative collision energy of the initial particle in the center-of-mass frame, Δ E is the difference of transition energy.
The normalized asymptotical continuum wave functions is given by
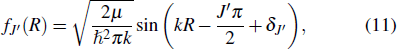 |
The total radiative decay cross-sections are evaluated with the optical potential approach.[9,10] In the processes of the ion-atom collisions, the transition probability is expressed by the imaginary part of a complex optical potential. The scattering wave FA (
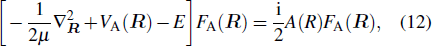 |
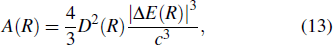 |
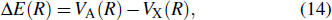 |
The radiative-decay cross-sections are determined by
 |
 |
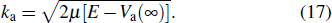 |
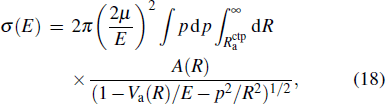 |
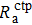
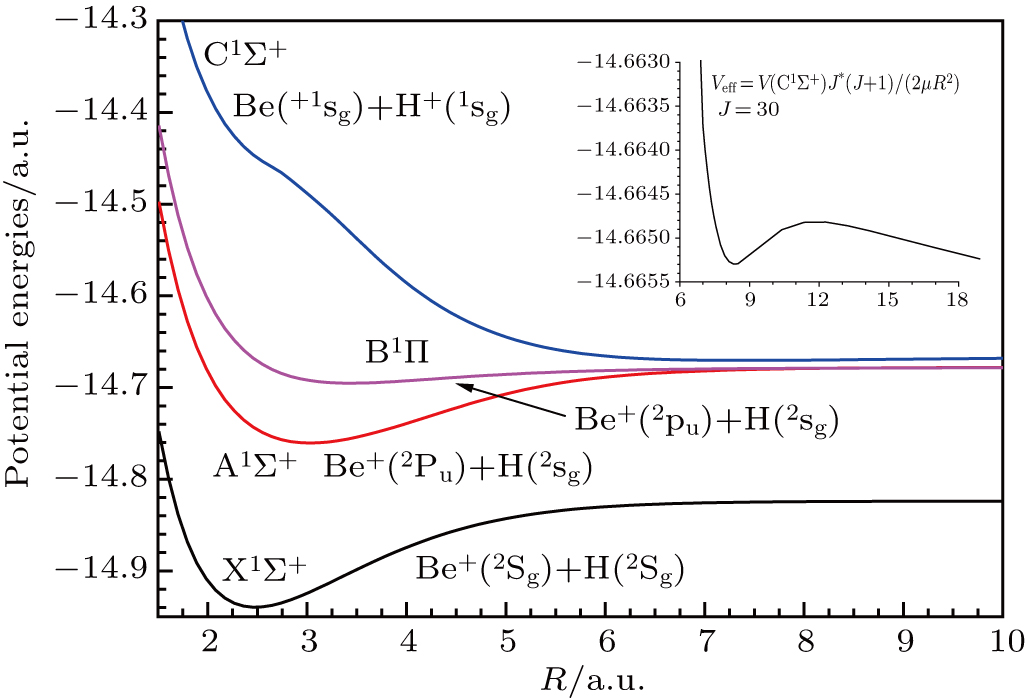
In Fig.
| Table 1. Spectroscopic constants for the low-lying bound states of BeH+. . |
As can be seen in Table
The dipole transition moments between singlet states are computed with MRDCI method, and dipole transition moments along the internuclear distance are presented in Fig.
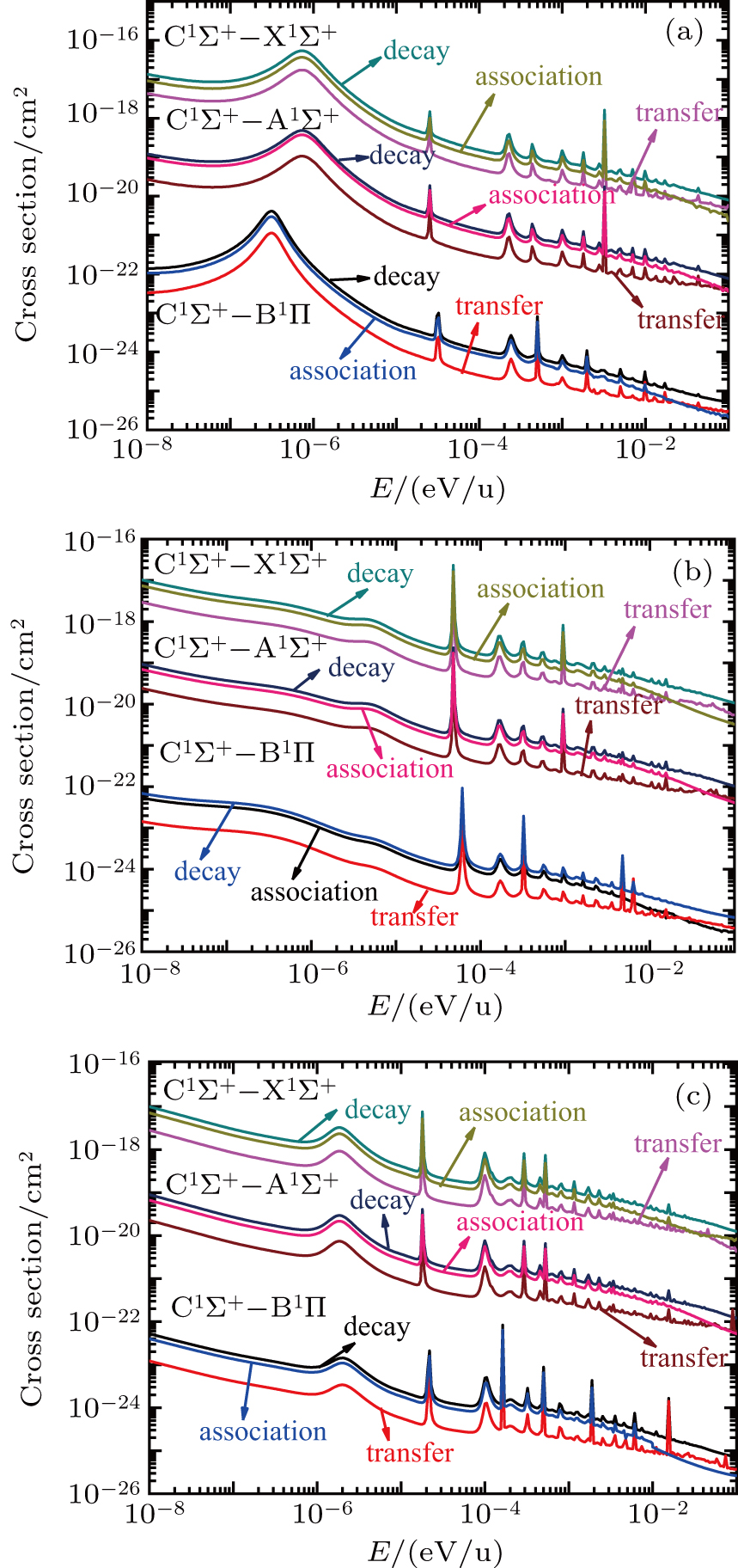
The results of present calculations for the processes (1) and (2), including the radiative decay, radiative charge transfer and radiative association cross-sections, are shown in Figs.
In Fig.
In the collisions complex of H+(D+, T+)–Be, there are obvious wells De for X1Σ+, A1Σ+, and B1Π states, which are 3.20 eV, 2.28 eV, and 0.48 eV, respectively, as shown in Table
For these resonance structures, appearing in the energy region of 10−6 eV/u–10−1 eV/u, are attributed to the presence of some specific rovibrational levels (v′, J′) in the entrance channel,[35–37] as shown in Fig.
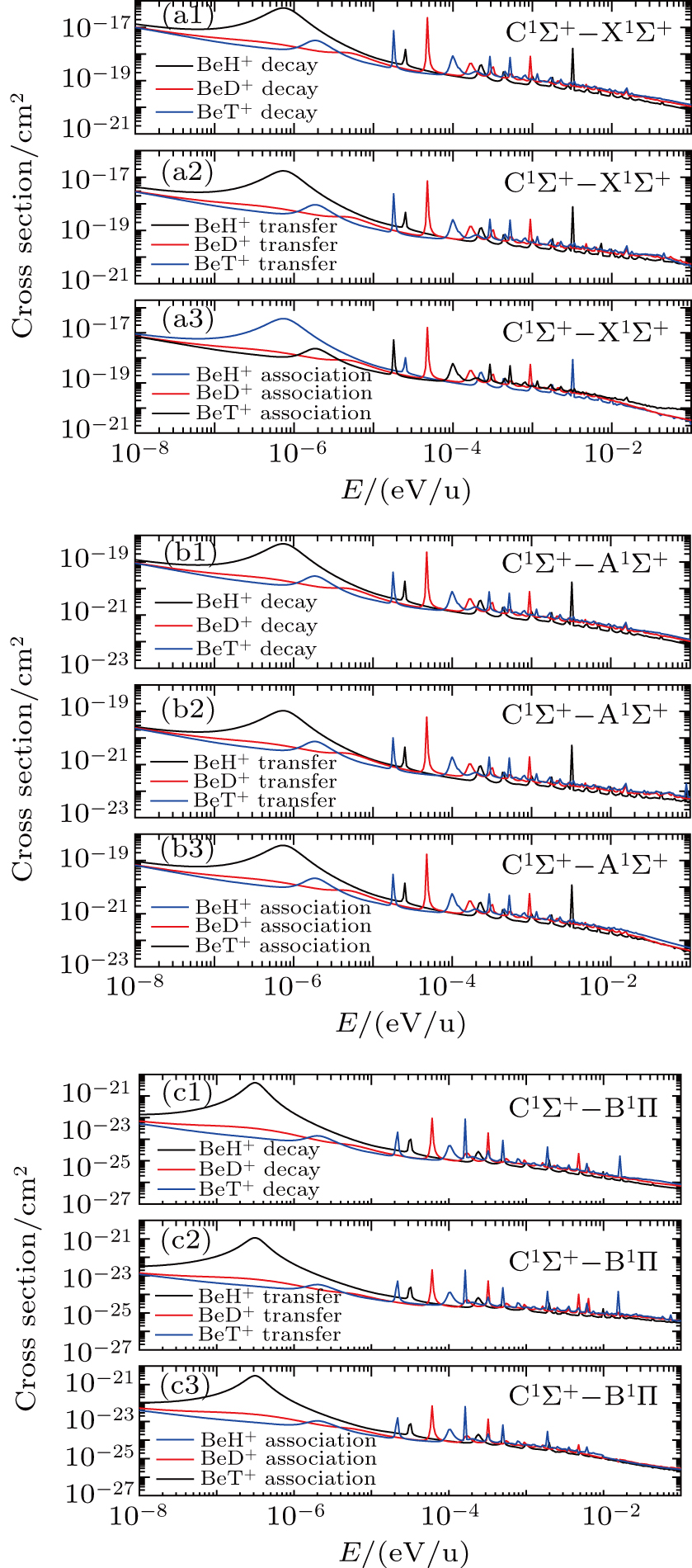
Significant isotope effects have been observed in low-energy non-radiative processes in ion-atom/molecule collisions,[38] it is interesting to see whether the isotope effects are important in the collision radiative processes. As shown in Figs.
In Fig.
Accurate PECs of singlet states of BeH+ are computed using the MRDCI method. The spectroscopic constants of X1Σ+, A1Σ+, C1Σ+-, and B1Π states are evaluated, and agree well with previous experimental data. On the basis of high precision PECs, the radiative association, radiative charge transfer and radiative decay cross-sections for the H+/D+/T+ + Be collisions in energy of 10−8 eV/u–0.1 eV/u are evaluated using the fully quantum, optical potential and semiclassical approaches. It is found that the radiative association process is dominant in the very low energy range around 10−8 eV/u–0.02 eV/u and the radiative charge transfer process becomes more important for higher energies. Moreover, there are rich resonance structures in the collision radiative cross-sections in the energy range considered, which are produced from the interaction between the quasi-bound rovibrational (J, v) states of the initial channel with the continuum state of the final channel. Isotope effects have been observed in the radiative decay processes, which are attributed to the kinematic effects due to the differences of the reduced masses of the collision complex and cannot be neglected in ion–atom collisions.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |