† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11575087 and 11175087).
We study the entanglement between the internal (coin) and the external (position) degrees of freedom in the dynamic and the static deterministic aperiodic quantum walks (QWs). For the dynamic (static) aperiodic QWs, the coin depends on the time (position) and takes two coins C(α) and C(β) arranged in the two classes of generalized Fibonacci (GF) and the Thue–Morse (TM) sequences. We found that for the dynamic QWs, the entanglement of three kinds of the aperiodic QWs are close to the maximal value, which are all much larger than that of the homogeneous QWs. Further, the first class of GF (1st GF) QWs can achieve the maximum entangled state, which is similar to that of the dynamic disordered QWs. And the entanglement of 1st GF QWs is greater than that of the TM QWs, being followed closely by the entanglement of the second class of GF (2nd GF) QWs. For the static QWs, the entanglement of three kinds of the aperiodic QWs are also close to the maximal value and 1st GF QWs can achieve the maximum entangled state. The entanglement of the TM QWs is between 1st GF QWs and 2nd GF QWs. However, the entanglement of the static disordered QWs is less than that of three kinds of the aperiodic QWs. This is different from those of the dynamic QWs. From these results, we can conclude that the dynamic and static 1st GF QWs can also be considered as maximal entanglement generators.
Recently the quantum walks (QWs)[1–4] have attracted extensive attention. This is because of the diffusion of QWs is faster than that of the classical random walks[1–9] and QWs are widely used in quantum information.[6–9] The another reason is that QWs can be used to simulate and explain dynamical behaviors in variety of the physical systems, such as Landau–Zener tunneling,[10] the Klein paradox,[11] and Bloch oscillations.[12] In addition, many experimental schemes have been suggested and reported to implement QWs, such as optical lattices,[13] trapped ions,[14–16] waveguide lattices,[17,18] light pulses in optical fibers,[19,20] and single photons.[21,22]
On the other hand, the entanglement in quantum state has far reaching application in information fields such as quantum cryptography, quantum computation, quantum teleportation, and quantum algorithms.[23–26] Only quantum system has this fantastic property.[27,28] In recent years, the entanglement of QWs has drawn much attention. Carneiro et al.[29] studied the entanglement of the homogeneous QWs between the coin and position degrees of freedom. They used the von Neumann entropy to measure the entanglement and found that the entanglement with Hadamard coin tends to be 0.872. Then, Vieira et al.[30] studied the entanglement of the dynamic disordered QWs and pointed out that the entanglement of the dynamic disordered QWs approaches one, the maximal value of entanglement, and the entanglement is independent of the initial condition of the walker. Therefore, the dynamic disorder QW can be considered as a maximal entanglement generator. They also studied the static disordered QWs and showed that the entanglement oscillate around a value smaller than 1. This is different from that of the dynamic disordered QWs.[31,32]
Since the discovery of quasicrystals by Shechtman et al.[33] and the studies of many experimental works of quasiperiodic superlattices,[34–36] a great deal of attention has been focused on studies of aperiodic systems. Despite the absence of translational invariance in these structures, they are perfectly ordered. Such systems can be regarded as intermediate between homogeneous and disordered systems. The aperiodic systems exhibit some unusual physical properties. For example, the electronic energy spectra of the Fibonacci lattice is singular continuous and the wave functions are critical, i.e., neither localized nor extended.[37,38] The widely studied aperiodic systems are the two-element Fibonacci,[35–45] generalized Fibonacci (GF),[39,46–50] and Thue–Morse (TM) systems.[39,45,51–54] They can be classified by different mathematical and/or physical properties. Burrows and Sulston defined the degrees of sequence disorder for two-element aperiodic sequences by the Shannon entropy.[55] They found that the second class of GF (2nd GF) sequences are more disordered than that of TM sequences, being followed by the first class of GF (1st GF) sequences. The degrees of sequence disorder for three kinds of the aperiodic sequences are between those of the disordered and homogeneous sequences. On the other hand, based on the wandering number, Luck showed that the quantum phase transition (QPT) of the Fibonacci, 1st GF and TM quantum Ising chain (QIC) belong to the same universality class of homogeneous QIC.[39] The QPT of the 2nd GF QIC is similar to that of the disordered QIC. Recently, the dynamic Fibonacci[40–46] and nonuniform QWs[56–60] have been widely investigated. It is found that the dynamic Fibonacci QWs leads to a sub-ballistic dynamic behavior characterized, i.e., σ(t) ∝ tα(0.5 < α < 1).[40] This behavior is between that of the homogeneous QWs (α = 1) and the dynamic disordered QWs (α = 1/2). It is also found that the dynamic behavior of the dynamic GF QWs is the sub-ballistic behavior and the α of the 2nd GF QWs is greater than that of the 1st GF QWs.[46] Therefore, there are two very interesting questions. One question is what is the entanglement of different dynamic (static) aperiodic QWs? Another is what is the relationship between the entanglement of different dynamic (static) aperiodic QWs and their relationship to entanglement of the disordered and homogeneous QWs? To address these questions, we study the entanglement of the dynamic and static aperiodic QWs.
The paper is organized as follows. The models of the dynamic and the static deterministic aperiodic QWs and the entanglement are introduced in Section
Consider a one-dimensional discrete QWs. The system can be described by a Hilbert space Hp ⊗ Hc, where Hp denotes the position space Z spanned by {|i⊗, i ∈ Z}, and Hc denotes the inner coin space spanned by {|↑⊗, |↓⊗}. A general state for a quantum walker can be written as[31]


When θ(i,t) is independent of the time and position, i.e., θ(i,t) = θ, the model becomes to the ordinary homogeneous QWs. In this paper, we consider two kinds of the aperiodic QWs: the dynamic and the static aperiodic QWs. For the dynamic aperiodic QWs, θ(i,t) = θ(t), i.e., the quantum coin is only dependent on the time. The time evolution of the system is obtained by applying U(t) to an arbitrary state at time t − 1, then the recurrence relations can be written as[31]
In order to study the deterministic aperiodic QWs, the θ(t) (θ(i)) takes two values α and β arranged in the generalized Fibonacci (GF) and the Thue–Morse (TM) sequences at the t-th step (i-th position) of the walker. The GF sequences for coin operators are generated from a seed (e. g., C(α)) by the following rule[39]
We can classify the GF sequences by a wandering index ω. The wandering index of the GF sequences is
The typical example of the 1st GF sequence is a sequences with m = n = 1, which is the well-known Fibonacci sequence. It is generated by the following rule:
Another well-studied aperiodic system is the TM system. The generating rule of the TM sequence for the coin operators is
Similarly, we also use the von Neumann entropy S of the reduced density matrix in the coin space to quantify the entanglement.[29–32] That is
To gain further insights into the asymptotic limit of S(t), we studied S(t) evolution over time by
In the following, we study the entanglement of the aperiodic QWs. Due to the nonuniformity of the aperiodic sequences, the numerical results need to be averaged as done in the random case.[31] In our numerical calculations, we generate a very long but finite the GF or the TM sequence of size L according to the rule (9) or rule (12). We select continuous sequence of size N from the sequence of size L (L ≫ N) randomly. N is the size of time steps (position spaces) for the dynamic (static) aperiodic QWs. Then we obtain the values of S(t). Finally, we perform the averaging over 100 realizations, and results averaging over more different selections are similar to those averaging over 100 different selections. In short, we use 〈S(t)〉 to denote the averaged entanglement. In our numerical calculations, we chose the initial state as
In Fig.
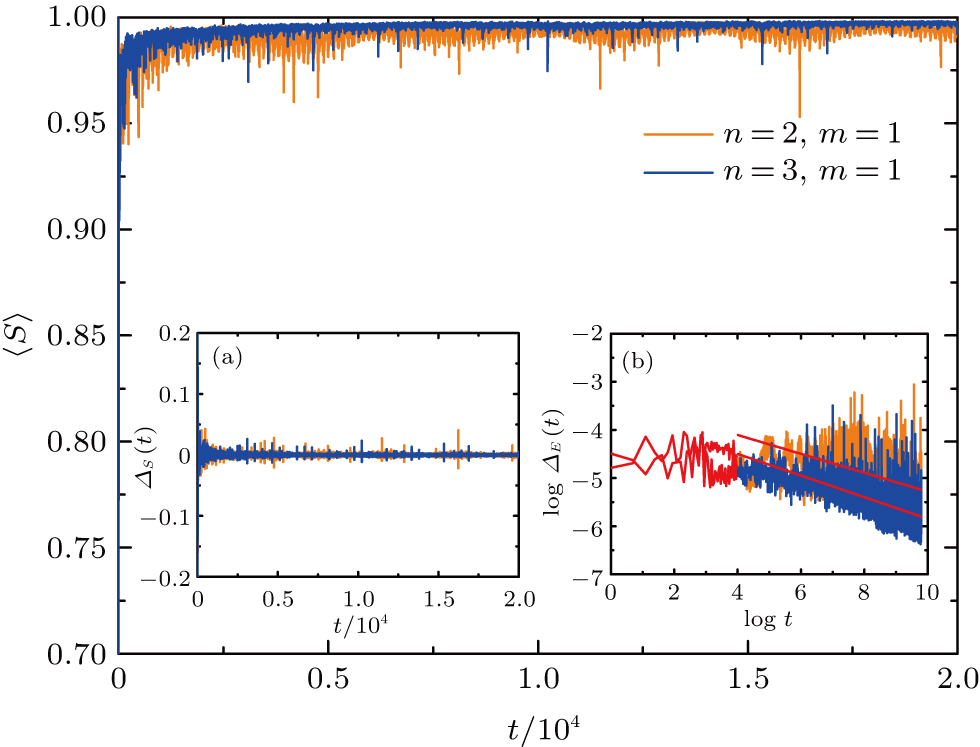
In order to study the entanglement of different sequences of the dynamic 1st GF QWs, we study the entanglement of the QWs with n = 2,m = 1 and n = 3, m = 1, respectively. The numerical results are shown in Fig.
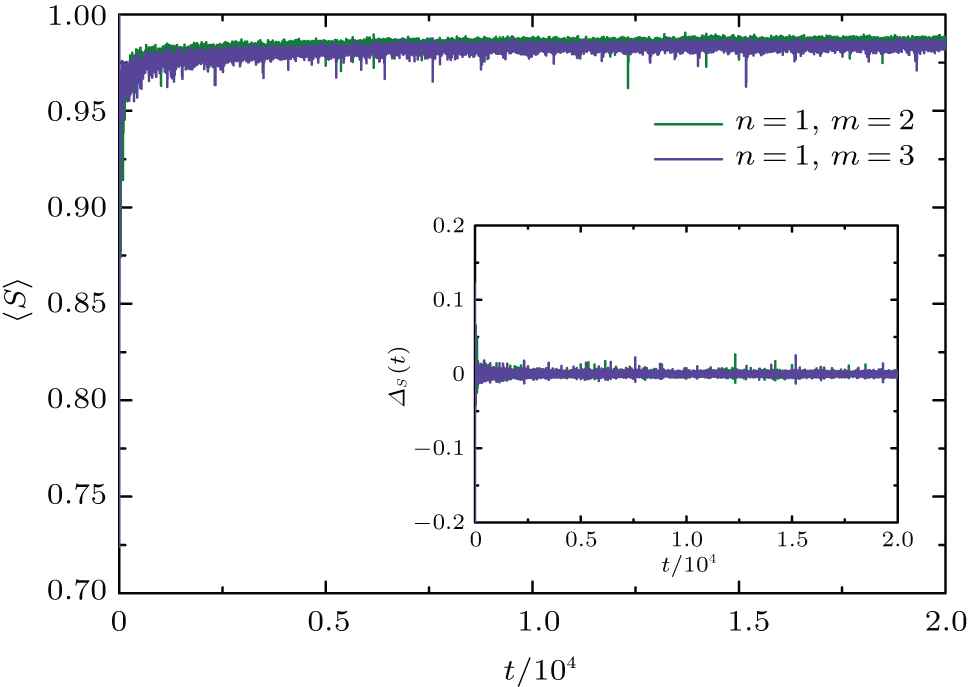
To compare the entanglement of the other aperiodic QWs, we give the numerical results of the dynamic 2nd GF QWs and the dynamic TM QWs in Figs.
 | Fig. 4. (color online) Averaged entanglement 〈S(t)〉 for the dynamic TM QWs with α = π/3, β = π/6. The inset is ΔS(t). |
In order to compare the entanglement of different aperiodic QWs with that of the homogeneous QWs and the disordered QWs, we give the results of 〈S(t)〉 as functions of time for those QWs in Fig.
For further understanding the entanglement of the dynamic QWs, we study the distributions P(ρ12) of the nondiagonal elements ρ12 of density matrix ρ. In Fig.
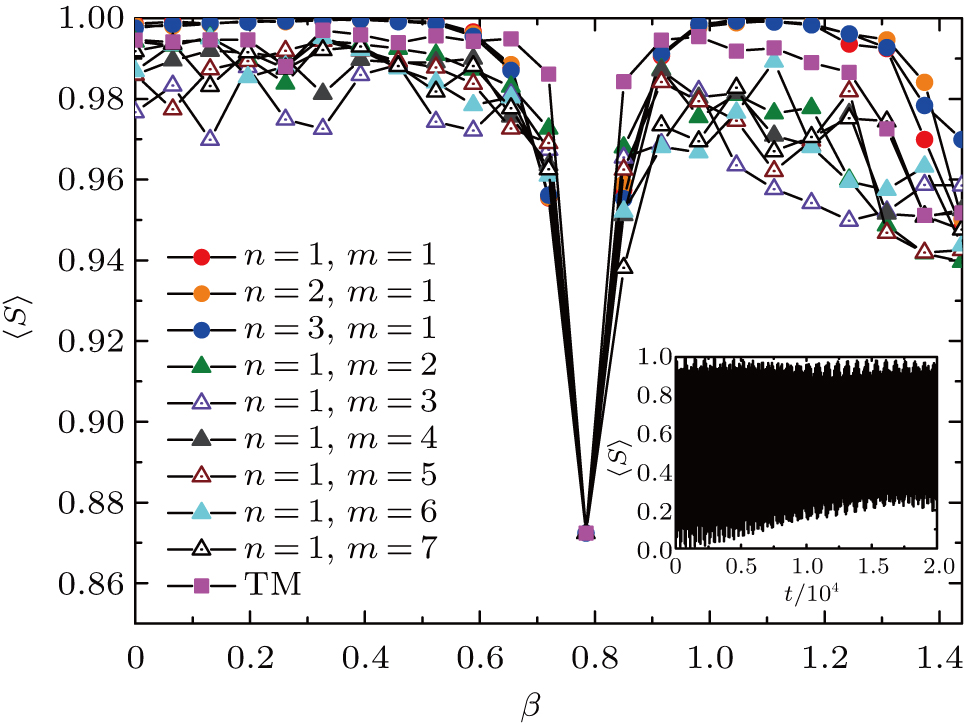
Finally, we analyze the entanglement of the dynamic aperiodic QWs with the different angles. In Fig. 
In Figs.
Similarly, from Figs.
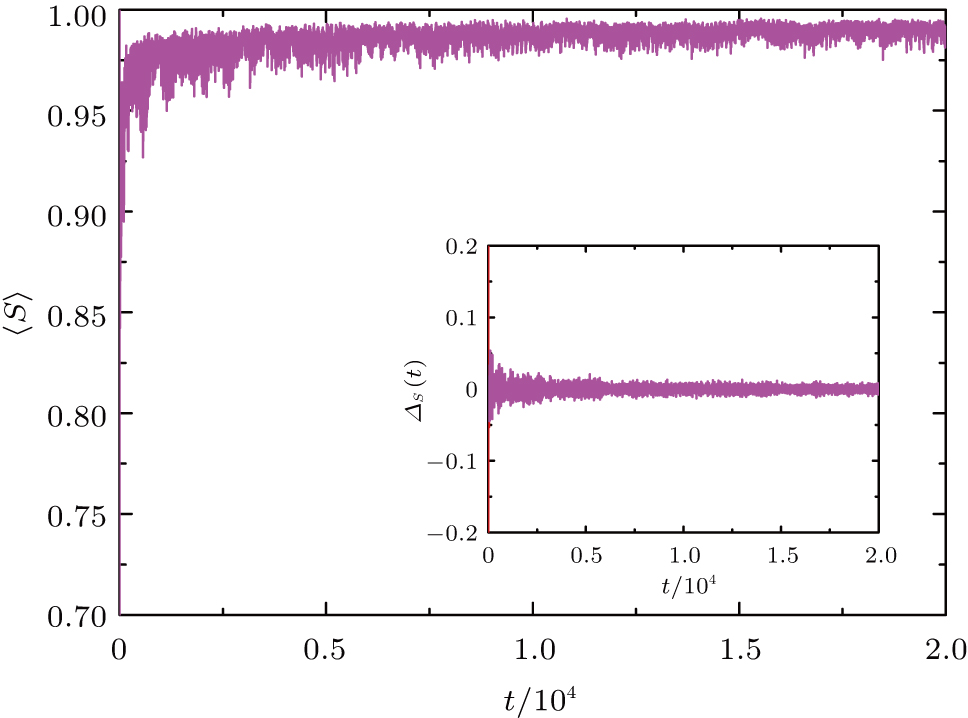 | Fig. 10. (color online) Averaged entanglement 〈S(t)〉 for the static TM QWs with α = π/3, β = π/6. The inset is ΔS(t). |
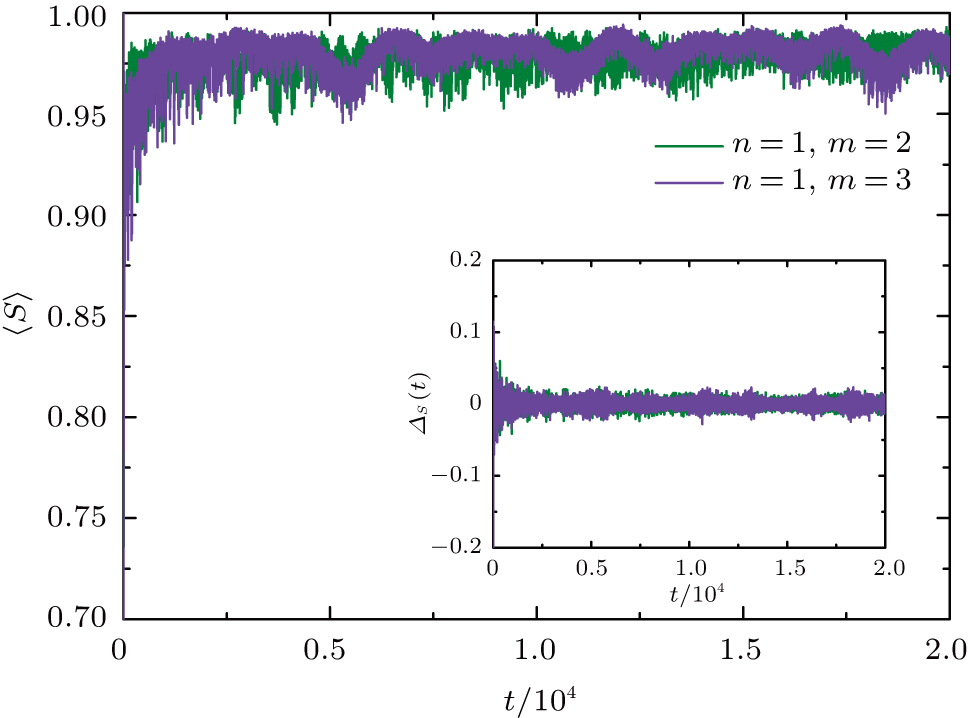
In Fig.
Similar to that in the dynamic aperiodic QWs, we also analyzing the distributions P(ρ12) of the nondiagonal element ρ12 of density matrix ρ for the static QWs (see Fig.
Similarly, we also study the entanglement of the static aperiodic QWs with different angles in Fig. 
In this paper, we have discussed the entanglement in the dynamic and static deterministic aperiodic QWs. For the dynamic aperiodic QWs, the entanglement of the 1st GF QWs can reach the maximal entanglement value, which is similar to that of the dynamic disordered QWs. The entanglements of the 2nd GF and TM QWs are all close to maximal value. For the static aperiodic QWs, the entanglement of 1st GF QWs also can reach the maximal entanglement value, which is different from that of the static disordered QWs. The entanglements of the 2nd GF and TM QWs are similar to those of these kinds of the dynamic QWs. From our results, we can conclude that both the dynamic and static 1st GF QWs are the deterministic maximal entanglement generators. At the same time, we found that whether dynamic or static QWs, the entanglement of the 1st GF QWs is greater than that of the TM QWs, being followed closely by the entanglement of 2nd GF QWs. The entanglements of three kinds of the dynamic aperiodic QWs are between those of the disordered and homogeneous QWs, however, the entanglements of three kinds of the static aperiodic QWs are all greater than those of the disordered and homogeneous QWs. Moreover, the classification of the aperiodic systems according to the entanglement of QWs is different from that by the quantum phase transition of the aperiodic quantum Ising chain[39] and that by the degrees of sequence disorder of those sequences.[55]
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] |