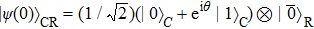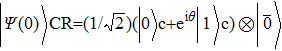† Corresponding author. E-mail:
Projects supported by the Natural Science Foundation of Guangdong Province, China (Grant No. 2015A030310354), the Science Foundation for Enhancing School with Innovation of Guangdong Ocean University (Grant Nos. GDOU2017052504 and GDOU2015050207), the Foundation of Excellent-Young-Backbone Teacher of Guangdong Ocean University (Grant No. HDYQ2017005), and the Fund of University Student Innovation and Entrepreneurship Team of Guangdong Ocean University (Grant No. CCTD201823).
The dynamics of the quantum Fisher information (QFI) of phase parameter estimation in a non-Markovian dissipative qubit system is investigated within the structure of single and double Lorentzian spectra. We use the time-convolutionless method with fourth-order perturbation expansion to obtain the general forms of QFI for the qubit system in terms of a non-Markovian master equation. We find that the phase parameter estimation can be enhanced in our model within both single and double Lorentzian spectra. What is more, the detuning and spectral width are two significant factors affecting the enhancement of parameter-estimation precision.
Quantum metrology[1,2] has played a role in several practical applications of the ultra-precise estimation of parameters bounded by quantum mechanics in recent decades. This aspect of quantum metrology has attracted many researchers to develop its measurement, preservation and application in both theory and experiments. The primary aim of quantum metrology is to enhance the precision of an unknown parameter. Usually, the exploitation of new techniques to enhance the precision of parameter estimation leads to technological advancement and scientific breakthroughs. The fast development of atomic spectroscopy,[3] optical interferometry,[4,5] gravitational wave detection,[6] magnetometry,[7,8] quantum frequency standards improvement,[9] and clock synchronization[10,11] can be attributed to the improvement of quantum metrology. Quantum Fisher information (QFI), which lies at the heart of quantum information theory and quantum estimation theory, can be used to measure the sensitivity of the state with respect to changes in a parameter. According to the quantum estimation theory, in general, the QFI characterized by the quantum Cramér–Rao (QCR) inequality[12] offers the ultimate achievable limit on precision. It imposes the lower bound of any unbiased estimator. A higher value of QFI means that the parameter can be estimated with a higher precision. Therefore, the QFI becomes the central problem to be solved.
Among various kinds of parameter estimation, great attention has been paid to the enhancement of phase estimation because a great deal of tasks are based on the problem of estimating the relative phase. As we known that any quantum system in the real world is in contact with its environment, the unavoidable interaction between the quantum system and its environment will cause decoherence, fluctuations or irreversible dissipative dynamics. Thus the quantum metrological protocols to fight against some kinds of decoherence have been explored in a wider context.[13–28] In this paper, we study phase estimation from an alternative time-convolutionless technique under two conditions of single Lorentzian spectral distribution and non-perfect photonic band gap, respectively. The analytical results of QFI are derived with respect to the fourth-order perturbation expansion. We show that parameter-estimation precision can be greatly preserved in the single Lorentzian spectrum under the non-Markovian case and partially trapped in the photonic band gap with a larger gap width. Moreover, the important factors affecting the enhancement of QFI are explored, and the corresponding physical mechanisms of these phenomena are given.
The paper is organized as follows. In Section
We briefly introduce some fundamental concepts of QFI. Assume that p(xi|θ) is a set probability density with measurement outcomes xi, where θ is the parameter to be estimated and 
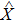
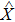
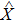
Analogous to the definition of classical Fisher information, the QFI associated with QCR inequality can be defined as
We build the model within an interaction between a qubit system and a zero temperature multi-mode reservoir. The Hamiltonian of the system can be written in the following form with a rotating-wave approximation[32]
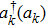
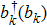
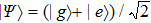
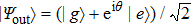
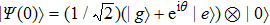
We develop a perturbation expansion for the time-convolutionless generator in powers of the coupling strength α,[34,35] so that γ(t) and S(t) can be expanded in the following form
As the first example, we consider the spectral density J(ω) with a single Lorentzian spectral structure[31,34]
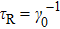
According to the demands of calculating precision, the fourth-order contribution of the perturbation expansion is a good approximation in the dynamical evolution,[34] such that
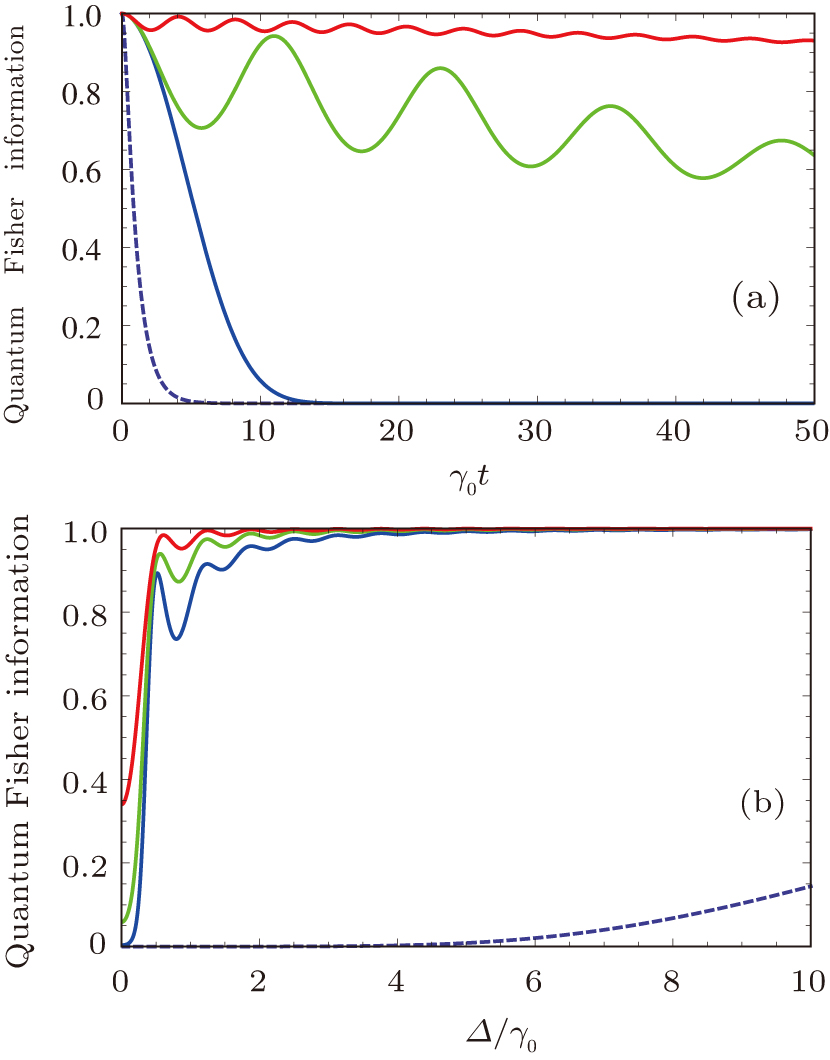
The QFI Fθ of a single Lorentzian spectral density can be calculated with the fourth-order perturbation expansion of γ4(t). Now we shall discuss the effect of enhancing parameter estimation which should be directly reflected from the dynamical evolution of the QFI with respect to Markovian and non-Markovian regimes for different spectral width λ and detuning parameter Δ. In Fig.
In the following, we want to investigate the relationship between the detuning and non-Markovian characteristics and QFI preservation. Figure
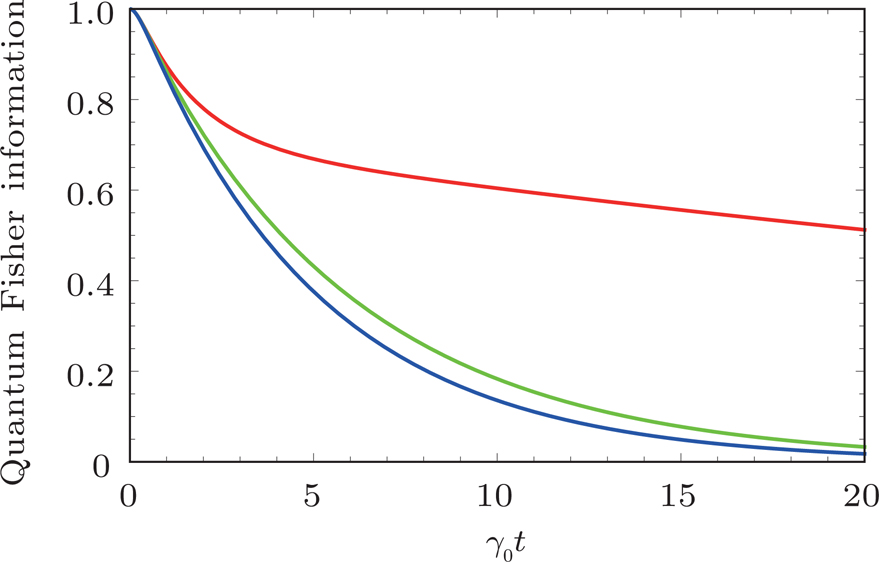
Next we consider another model for a qubit system in a photonic band gap, which was first introduced by Garraway[36] in 1997. The double Lorentzian spectral density is of the form
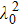
In conclusion, we have proposed a time-convolutionless scheme to enhance the parameter-estimation precision of a dissipative qubit system coupled to zero temperature surroundings. By employing a fourth-order perturbation expansion, we have derived the analytical results of QFI under two different environments: 1) in the single Lorentzian spectral structure, QFI preservation is affected by the detuning and correlation time of the reservoir; and 2) in the double Lorentzian spectral structure, which is called a non-perfect photonic band gap, the preservation of QFI is only affected by the spectral width.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] |