† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11675084 and 11435005), the Fund from the Educational Commission of Zhejiang Province, China (Grant No. Y201737177), Ningbo Natural Science Foundation (Grant No. 2015A610159), and the K CWong Magna Fund in Ningbo University.
In this manuscript, a reduced (3+1)-dimensional nonlinear evolution equation is studied. We first construct the bilinear formalism of the equation by using the binary Bell polynomials theory, then explore a lump solution to the special case for z = x. Furthermore, a more general form of lump solution of the equation is found which possesses seven arbitrary parameters and four constraint conditions. By cutting the lump by the induced soliton(s), lumpoff and instanton/rogue wave solutions are also constructed by the more general form of lump solution.
Rogue waves correspond to large-amplitude waves are extreme events that seldom appear on the ocean surfaces. Such waves can be accompanied by deep troughs (holes), which occur before and/or after the largest crest. In the last decades, a large interest including theories and experiments has spread from oceanography into several other areas of research, such as nonlinear optical systems,[1–3] plasmas,[4–6] fluid dynamics and atmosphere,[7–9] Bose–Einstein condensations (BECs),[10,11] financial system,[12,13] microwave oscillators,[14] capillary flow,[15] etc. Various physical models of the rogue wave phenomenon have been intensively developed and many laboratory experiments[16–18] conducted. These investigations makes scientists to understand the physics of the huge wave appearance and its relation to environmental conditions. Though the origin of rogue waves is still a matter of debate,[19] there are two important and common features characterizing rogue wave phenomena which have been known and accepted: 1) its amplitude is more than twice (or 2.5 times) of the average amplitude of the significant wave height; 2) a rogue wave “appears from nowhere and disappears without a trace”, in other words, rogue wave is believed to be unpredictable.
Many nonlinear physical models are used to describe rogue waves. For example, the lump waves, known as a kind rational function solutions, is an algebraically localized wave decayed in all space directions and exists in all time which can be used to describe rouge waves in some sence. Recent studies show lump solutions have attracted more and more attention. Many physical systems, such as (2+1)-dimensional KPI equation, BKP equation, KdV equation, CDGKS equation, and Ito equation have been proved to possess lump solutions.[20–23] Generally, there are many methods to search for lump solutions, such as the multiple variable separation method,[24] the common expression method,[25] etc. Moreover, recent study shows the interactions between lumps and other nonlinear waves such as Refs. [26]–[30]. These progress are very helpful in understanding of the physical mechanisms of the rogue wave phenomenon.
On the other hand, in quantum field theories the instantons studies allow scientists to see the previously hidden logarithmic structure of the states and operators.[31,32] Physicists believe that instantons are the key to explore the interactions principle in the standard model. Studies exhibit that instantons have been shown in integrable systems, such as DS equation[24] via the multiple linear variable separation approach.
In this paper, we consider a (3+1)-dimensional nonlinear evolution equation (NEE)
This paper is organized as follows: In the next section, we first introduce the known form of the lump solutions for the reduced nonlinear evolution equation, then extend a more general form to obtain lump solutions with maximum numbers of arbitrary parameters. In Section
Now we try to construct the bilinear formalism of the NEE Eq. (
Substitute Eq. (
Based on the property of the binary Bell polynomials and the bilinear operator, let q = 2ln (f), then u is related to f by
To construct the lump solutions of the NEE Eq. (
In this section, we seek lump solutions of the equivalent equation (
Substituting Eq. (
It is necessary to point out that in order to solve the ten determining equations (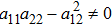
Applying the results into Eq. (
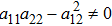
We can conclude that the solutions (
The results show that in order to solve the ten determining equations (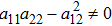
To contain more parameters in the solution, we take a special ansatz
Substituting Eqs. (
It is plausible that our work is similar to others, but using two requirements of ωm and f0, we actually decrease the constraint conditions. And we will check that the solutions have a maximum number of free parameters, in other words, the arbitrary parameters are meaningless when n is no limiting.
First we consider n = 2. It can be seen that there are nine parameters totally, including k1, k2, p1, p2, ω1, ω2, α1, α2, and f0. But according to Eq. (
Then we take n = 3, the solution contains 13 parameters for {km, pm, ωm, αm}, m = 1, 2, 3, and f0 but only 11 parameters are independent according to Eq. (
For n ≥ 4 case, because the numbers of constraint conditions for ωk and f0 is more than or equal to 5, the total numbers of independent parameters are less than or equal to 6. Compared with n = 3 case, the numbers of independent arbitrary parameters decreases. Thus it is impossible for us to find more arbitrary free parameters in the lump solutions for n ≥ 4.
So we conclude that the solution of Eqs. (
According to Eq. (
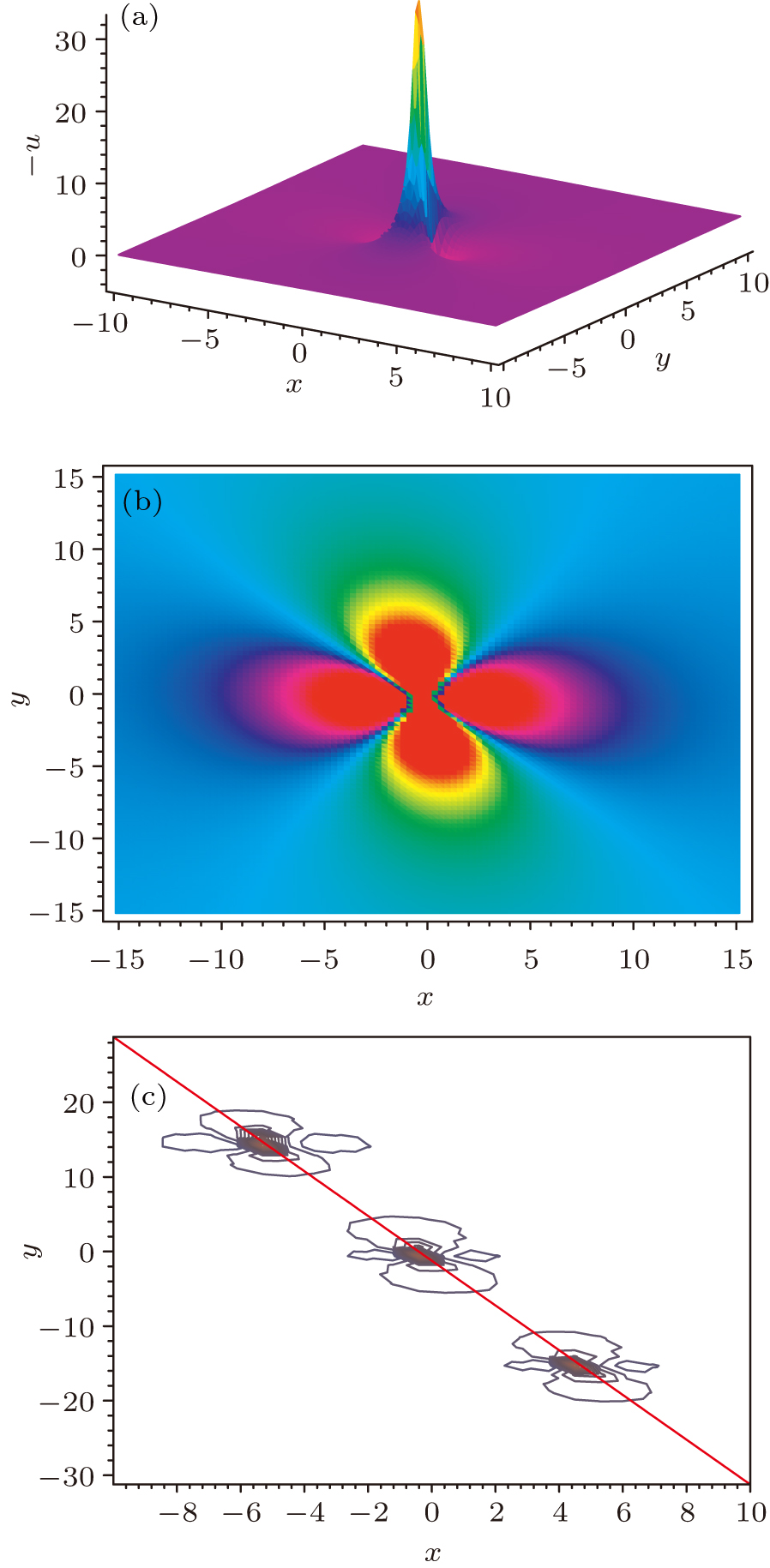
Based on Eq. (
A figure of a lump is shown in Fig.
It should be pointed out that when z = y, we can also find the lump solution of the NEE. One can easily find that the lump solution in this case contains five arbitrary constants which is much more simple than the case z = x. Here we do not show it in detail.
A lumpoff is a cutoff lump, which is a lump cut by something (say, a soliton) before or after a special time (off-time) that means the lump exists only before or after the off-time. In this section, we focus on the lumpoff solution to the reduced NEE.
To find the lumpoff solution, we take the ansatz
With a direct calculation by substituting the ansatz Eq. (
It is interesting that the results demonstrate a special soliton induced by lump. Equation (
According to Eq. (
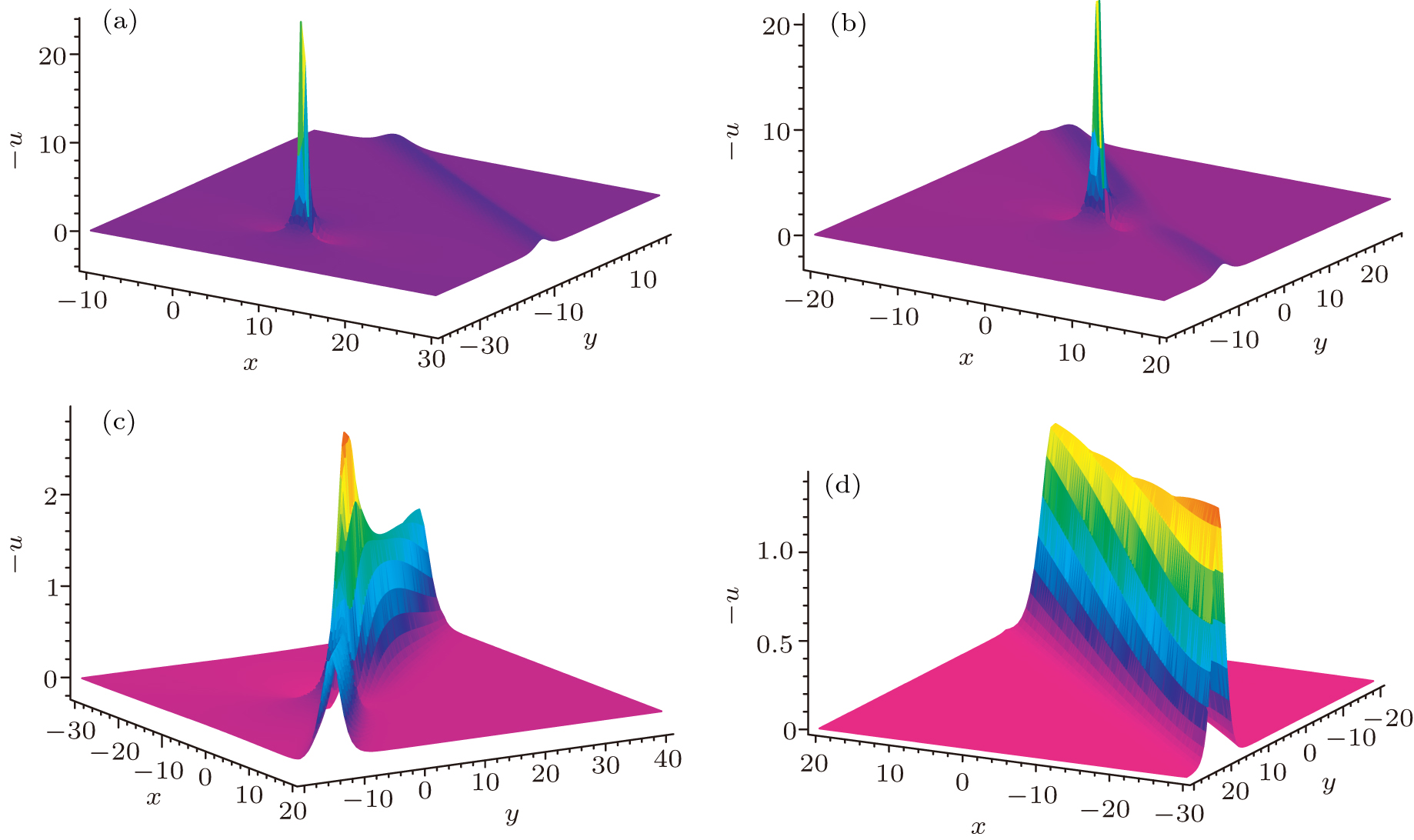
Based on the transformation u = −6(ln f)xx, we obtain the lumpoff solution of the NEE for z = x
For instance, if we select the arbitrary parameters as
Because the lump part remains unchanged, the corresponding positions of the lump are Eq. (
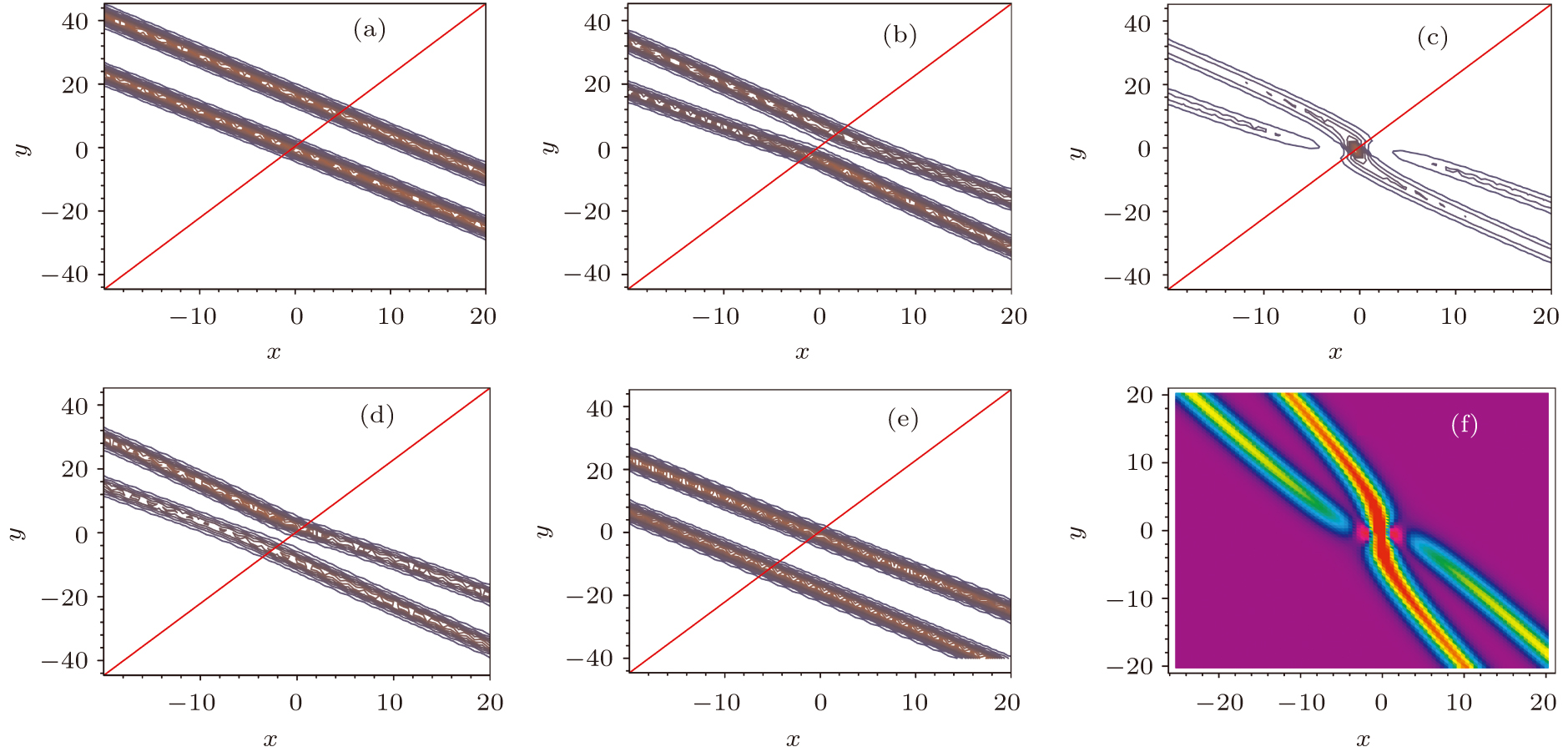
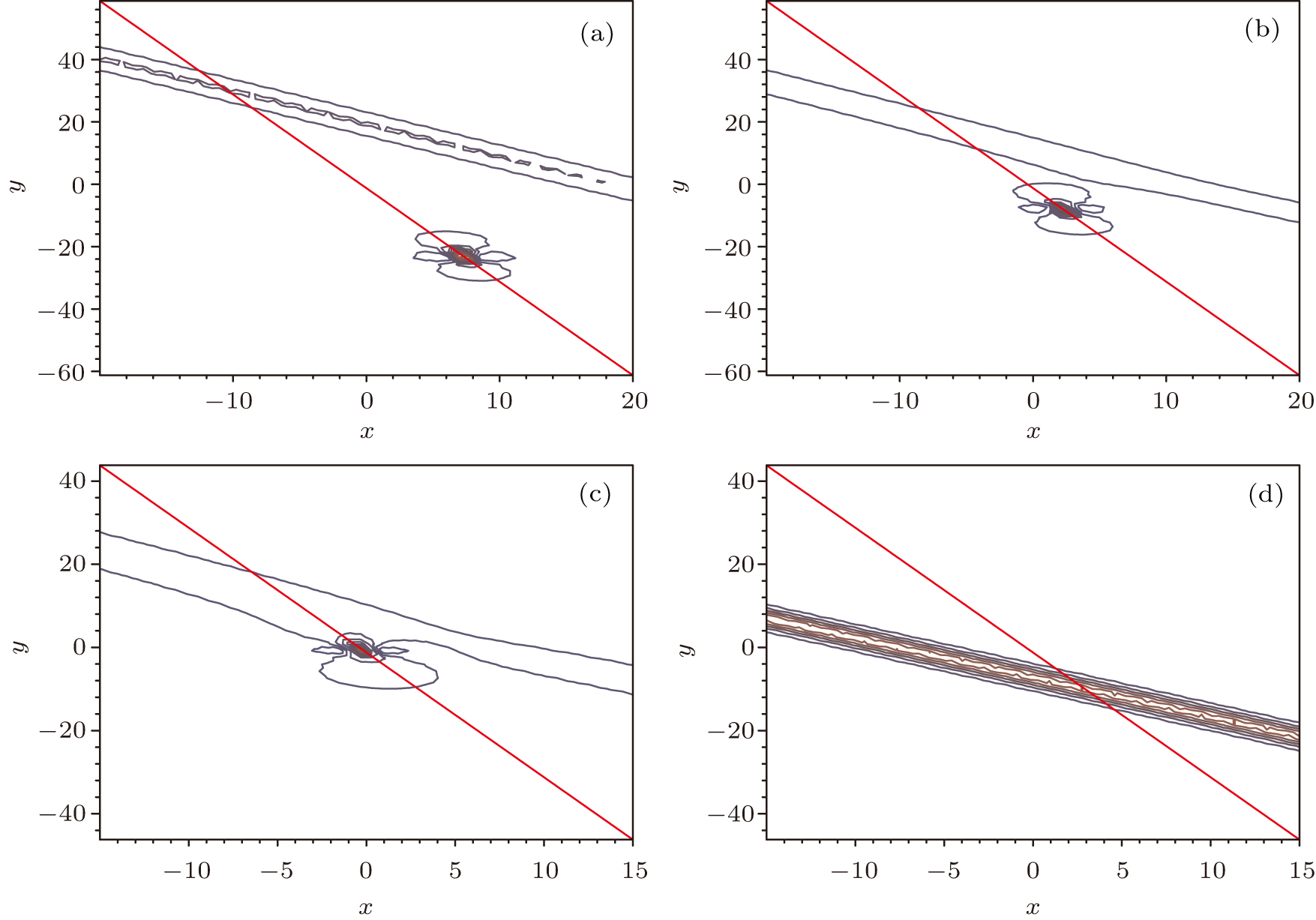 | Fig. 3. (color online) The path and the positions of the lump at (a) t = −15, (b) t = −5, (c) t = 0, and (d) t = 25. |
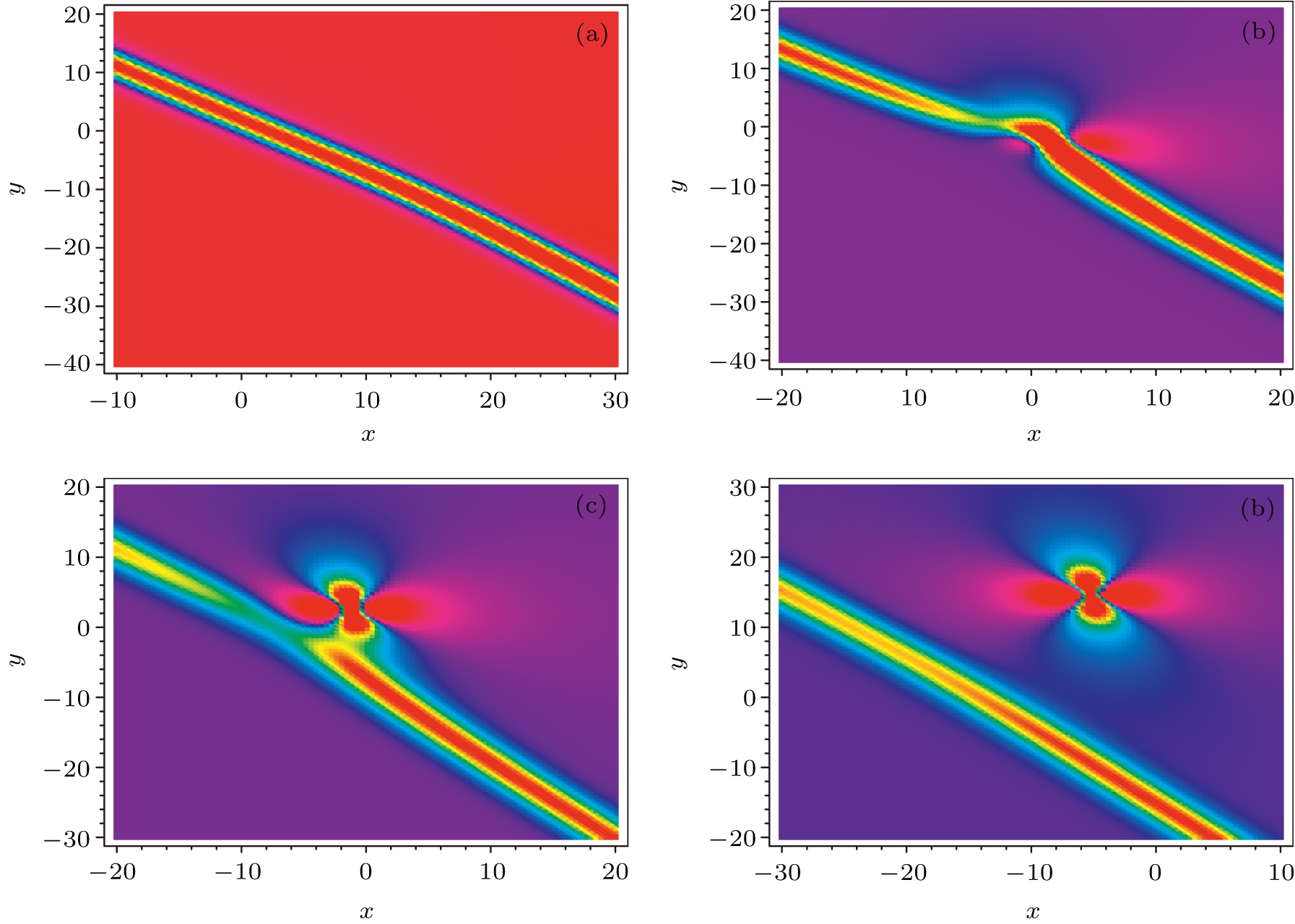
Figure
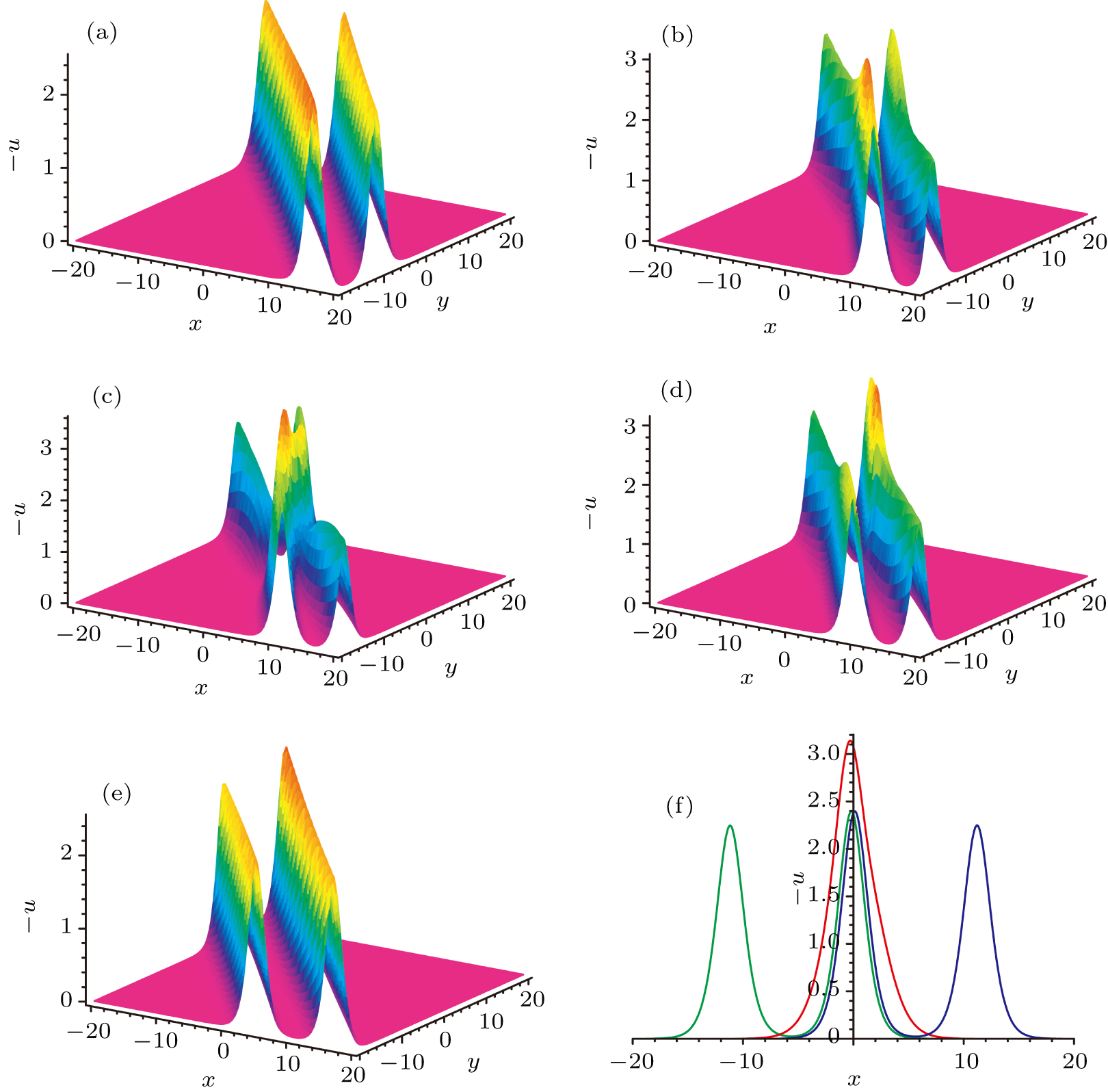
The lumpoff solution is a lump cutoff by a induced line-soliton. A lump can also be confined between two off-times, forward-off-time (tf) and backward-off-time (tb). In other words, the lump appears at tf and disappears at tb ≥ tf. As known to all, an instanton/rogue wave is a localized wave decayed in all space and time directions. Thus, an algebraic rogue wave/instanton can also be produced by cutting a lump between two off-times, forward-off-time (tf) and backward-off-time (tb).
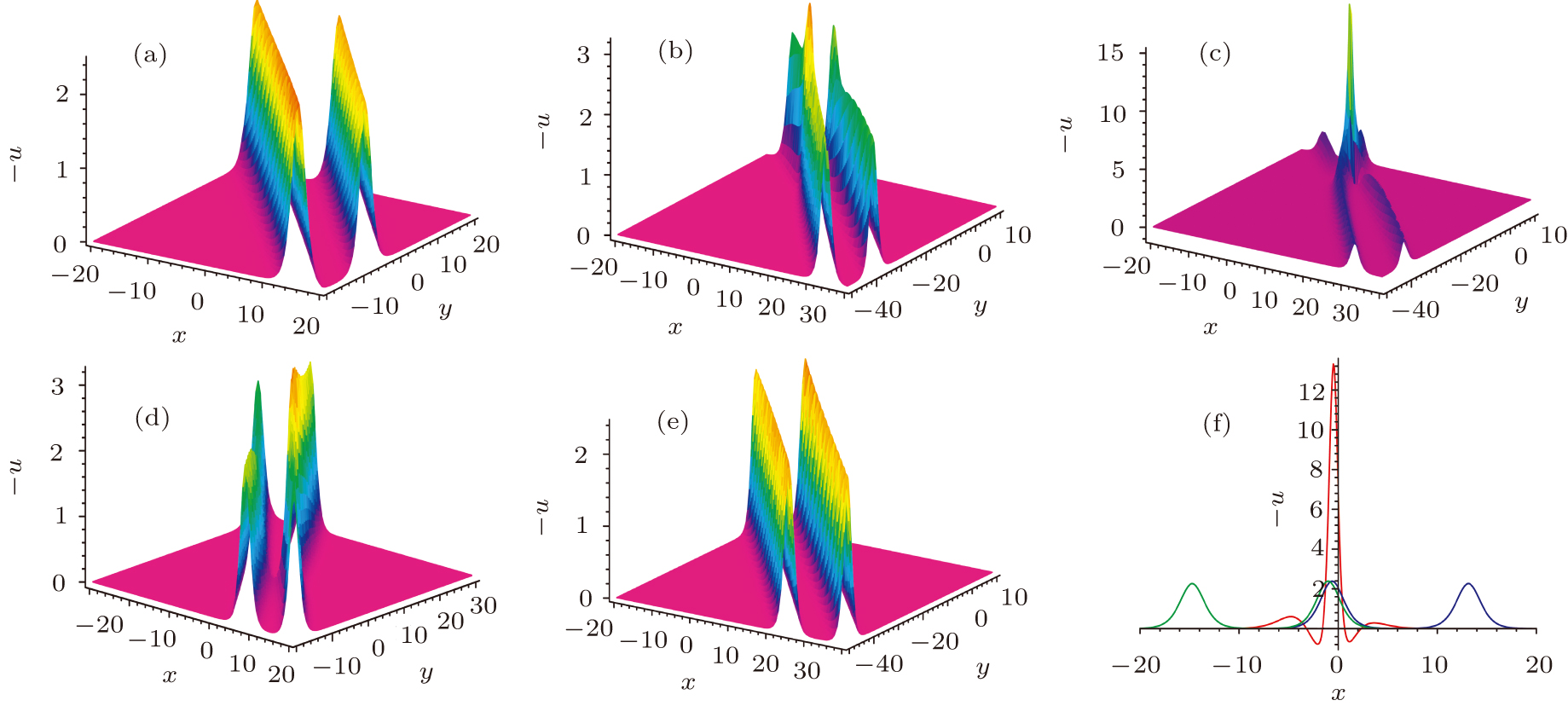
To obtain the instanton/rouge wave solutions to the NEE, we assume f is in the form of
We obtain the instanton/rouge wave solution Eq. (
Moreover, the maximum value of wave hight of the instanton/rogue wave is
Our results show novel generating and prediction mechanism for this kind of rogue waves. Because the twin-soliton includes enough information (k0, p0, and ω0) of the invisible lump (algebraic) part (a11, a22, and a12), the wave height of the rogue wave may be known.
Because the lump part remains unchanged, once the lump emerges out from the soliton, it will keep its path and velocity until it meets the other soliton.
For example, we take the correlative data as
For the general amplitude, we obtain the instanton solution to the NEE. If we choose a1 = 7, x0 = 0 with other parameters invariant in Eq. (
In summary, a (3+1)-dimensional nonlinear evolution equation (NEE) is studied in this paper. The bilinear formalism is constructed by binary Bell polynomials theories, and then a lump solution is found to the special NEE for z = x. With the help of the obtained lump solution, a more general form of lump solution is found. The more general form of lump equations possesses seven arbitrary parameters and four constraint conditions. Furthermore, by cutting the lump by the induced solitons, the lumpoff and instanton/rogue wave solutions are constructed.
It should be emphasized that the soliton is induced by the lump itself. A special dispersive relation is found for the soliton being determined by the lump. If the lump does not exist, the soliton will also disappear.
By cutting a lump between two off-times, the instanton/rogue wave solution is found. If the lump reaches a large amplitude, it will become a rogue wave, or be an instanton for general amplitudes. It is concluded that the amplitude of the wave height is related to both lump and the induced solitons. Because the visible two-solitons show all the information of the lump, it is possible to predict the exitance of a rogue wave.
It is interesting that our method is effective for other nonlinear system which provides a possible way to find this kind of rogue waves in physical systems due to the connection of the NEE and other systems. Meanwhile, the progress in understanding the physics of the instanton/rogue wave phenomenon and development of adequate mathematical models is very significant because it is possible to find instanton/rogue wave in physical systems.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] |