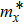† Corresponding author. E-mail:
Project supported by the National Key R&D Program of China (Grant No. 2017YFB0305800).
The band structure, density of states, optical properties, carrier mobility, and loss function of graphene, black phosphorus (BP), and molybdenum disulfide (MoS2) were investigated by the first-principles method with the generalized-gradient approximation. The graphene was a zero-band-gap semiconductor. The band gaps of BP and MoS2 were strongly dependent on the number of layers. The relationships between layers and band gap were built to predict the band gap of few-layer BP and MoS2. The absorption showed an explicit anisotropy for light polarized in (1 0 0) and (0 0 1) directions of graphene, BP, and MoS2. This behavior may be readily detected in spectroscopic measurements and exploited for optoelectronic applications. Moreover, graphene (

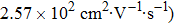
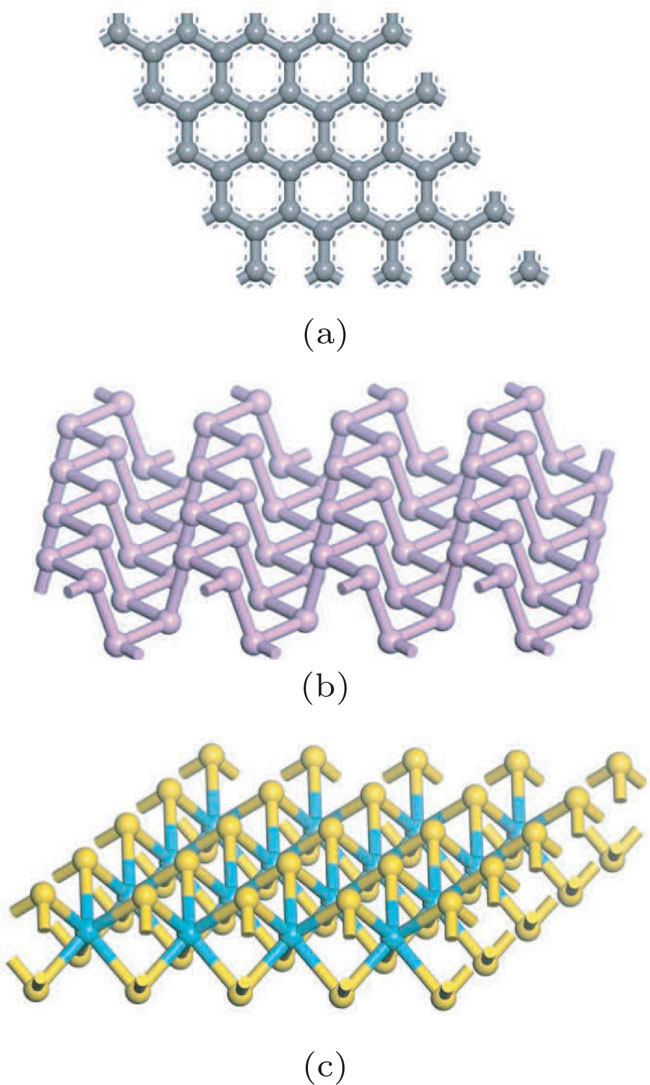
Van der Waals crystals, including graphene, black phosphorus (BP), and transition-metal dichalcogenide nanomaterials that can be described as MX2 (M= Mo, W, Nb, Ta, Ti, Zr, Hf, Re; X= S, Se), are currently under intensive research, driven by the wide potential application in high performance optoelectronic devices, such as a field-effect transistor (FET). They can be used in passively mode-locked and passively Q-switched fiber laser or solid laser as the saturable absorber. Graphene, BP, and MoS2 have the advantages of a moderate electronic band gap, a reasonably high carrier mobility, and excellent electrode–channel contacts because of the layer-controllable crystal structure. Graphene is a gapless semiconductor with the advantage of high carrier mobility due to its very low carrier effective mass.[1] However, the application of graphene in semiconductor materials is limited, also because of the zero-band gap. For this reason, the emergence of few-layer BP has attracted much attention. Few-layer BP has advantages of high mobility, high in-plane anisotropy, a moderate band gap (0.3–1.5 eV), and linear dichroism.[2] It can be widely used in optical detection and communications. BP is an intrinsic p-type semiconductor, which is different from graphene and MoS2.[3] Compared with graphene and BP, MoS2 has more application value in hydrogen adsorption and storage due to a band gap of 1.3–1.8 eV.
It is difficult to measure the band gaps of few-layer graphene, BP, and MoS2 experimentally. To guide the experimental study, the electronic structure of graphene, BP, and MoS2 were calculated using the generalized gradient approximation (GGA) based on the density functional theory (DFT). Rudenko et al., Cai et al., and Qiao et al. calculated the properties of BP from monolayer to five-layer.[1,2,4] Wang et al., Hu et al., and Phuc et al. calculated the properties of MoS2.[5–7] Although the band and the lattice structures of few-layer graphene, BP, and MoS2 have been extensively studied, detailed research on optical properties is rarely reported. The loss function represents the energy loss of the electrons quickly through material and electron excitation in the interior or surface of the material.[8] Very few researchers have studied this aspect. In addition, most of these studies were independent, a comparative and comprehensive study on few-layer graphene, BP, and MoS2 has not yet emerged.
In this paper, a first-principles calculation theory was used to study the structural properties, energy gap, the density of states (DOS), the partial density of states (PDOS), optical properties, carrier mobility, and loss function of few-layer graphene, BP, and MoS2. To predict the band gap of few-layer BP and MoS2, the relationships between the number of layers and the band gap were built. In addition, the absorption and carrier mobility were analyzed in detail.
All of the models were built and optimized with the CASTEP module, with the generalized-gradient approximation (GGA) of the exchange–correlation functional (RPBE). The cutoff energy for the plane wave was set to 400 eV. The convergence tolerance of force on each atom during structure relaxation was reduced to less than 0.03 eV/Å. The maximal displacement of atoms was reduced to less than 1 × 10−3 Å. The total energy variation of the system was reduced to less than 2.0 × 10−6 eV/atom. The internal stress between atoms was reduced to less than 0.05 GPa. The SCF tolerance was reduced to less than 1.0 × 10−6 eV/atom. The Brillouin zone integration was performed with 50 × 50 × 1 k-points for graphene, BP, and MoS2. To improve the speed of this calculation, we used higher symmetry k points in BP and MoS2 calculation. The vacuum distance of 20 Å was used in order to isolate the slabs from their periodic images, for graphene, BP, and MoS2 from monolayer to five-layer.[9]
Figure
| Table 1.
Lattice constants of graphene, BP, and MoS2. . |
Bulk BP is an orthorhombic crystal with the Cmca space group. The puckered layer is composed of zigzag direction and armchair direction. Based on bulk BP, the structures of monolayer and few-layer phosphorene were obtained by mechanical exfoliation.[16] The monolayer BP has a puckered honeycomb structure in which a phosphorus atom covalently bonds with three adjacent atoms.[17] Due to the lone pairs electrons associated with each atom, the sp3 hybridization is formed by two P atoms with three bonding orbitals.[4,18] The lattice parameter a increases and b decreases from monolayer to five-layer BP. There is an abrupt reduction of a from the monolayer to the bilayer due to the interlayer interactions in the bilayer.[1] Few-layer MoS2 has the S/Mo/S sandwich structure, interlinked by van der Waals force. In contrast from BP, the lattice parameters of MoS2 barely change from monolayer to five-layer. The calculated geometric structures are in good agreement with the previous theoretical and experimental results. Therefore, the theoretical calculation is correct.
Figure 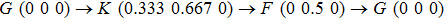
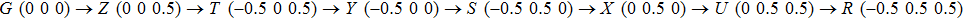

Figure
Figure
Figure
 | Fig. 5. (color online) The absorption spectra of (a) (1 0 0) graphene, (b) (0 0 1) graphene, (c) (1 0 0) BP, (d) (0 0 1) BP, (e) (1 0 0) MoS2, and (f) (0 0 1) MoS2. |
Among graphene, BP, and MoS2, graphene has the highest absorption threshold. The absorption and transmission of monolayer graphene are 2.3% and 97.7%, respectively.[20] Therefore, it can be widely used in solar cell and liquid crystal device window layer field. The absorption threshold of BP is lower than that of MoS2, because of the smaller band gap. Given the band gap variations, the absorption thresholds of BP and MoS2 are decreased from monolayer to five-layer. We can determine the sample orientation using the linear dichroism of BP and MoS2 easily. Once the sample orientation is determined, it is easier to manufacture electrodes by using the highest-mobility direction of sample in an FET-type device.[1]
The carrier mobilities of graphene, BP, and MoS2 are calculated according to[1]

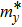


| Table 2.
Predicted carrier mobilities of graphene, BP, and MoS2. . |
From Table 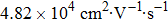







Figure
In brief, by first-principles calculation, we have shown that the band gaps of BP and MoS2 are strongly dependent on the number of layers. The band gap of MoS2 is 1.002–1.806 eV, and that of BP is 0.511–1.227 eV, from monolayer to five-layer. The graphene is a zero-band-gap semiconductor. The relationship of the layers and the band gap is built to predict the band gap of few-layer BP and MoS2. The absorption shows an explicit anisotropy for light polarized in (1 0 0) and (0 0 1) directions of graphene, BP, and MoS2. This behavior may be readily detected in spectroscopic measurements and exploited for optoelectronic applications. Graphene, monolayer BP, and MoS2 have high carrier mobility. The decreasing trend for carrier effective masses with increasing number of layers suggests a higher mobility for multilayer BP compared to monolayer BP. Among graphene, BP, and MoS2, BP has superior optical storage efficiency, which can be used in optical storage devices. These results suggest that graphene, BP, and MoS2 have abundant opportunities for a plethora of new electronic applications.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] |