The liquid phase separation phenomena have been extensively studied^[1–5] and their significant effect on structures and properties of various materials have been revealed.^[6–13] As the great potential application of high entropy alloys and bulk metallic glasses, liquid phase separation is attracting more and more attention.^[14,15] It is interesting that some peritectic and eutectic alloys characterized by a large positive enthalpy of mixing and a nearly flat liquidus curve show a miscibility gap in the metastable undercooled liquid, such as Co–Cu^[16] and Fe–Cu.^[17] The metastable liquid phase separation behaviors of the Co–Cu and Fe–Cu systems have been intensively investigated. It is found that the critical temperature of the miscibility gap of the Fe–Cu system is 120 K higher than that of the Co–Cu system.^[18,19] When a third component is added into the above binary alloys characterized by liquid phase separation in the undercooled state, the resulting ternary alloy system also shows a metastable miscibility gap over a certain composition range. Much work has been done on the phase diagram and solidification behaviors of the Cu–Co–Fe ternary alloy system. Jellingahus^[20] and Maddocks and Claussen^[21] first investigated vertical sections of the phase diagram of Cu–Co–Fe ternary alloy system using thermal analysis and metallography, but they did not observe immiscibility behavior in this ternary system. Isothermal sections of the phase diagram at several temperatures have been obtained.^[22] Munitz et al.^[23] observed liquid phase separation in Cu–Co–Fe alloys containing 52–79 at.% Cu at high cooling rates. Kim et al.^[24] measured the liquidus and demixing temperatures of some Cu–Co–Fe alloys by means of a pyrometer in the electromagnetic levitation state. Bamberger et al.^[25] evaluated the stable and metastable Cu–Co–Fe phase diagrams. Wang et al.^[26] calculated the phase equilibria in Fe–Cu–X (X: Co, Cr, Si, V) ternary systems and obtained the miscibility gaps theoretically. Applying high temperature differential thermal analysis technique, Cao and Görler^[27] precisely determined the liquidus and the miscibility gap over a wide composition range for this system. The boundary lines of the miscibility gap, which are determined for the three quasi-binary cross-sections of the Cu–(Fe,Co) alloy system, show remarkably flat domes. It is found that the directly determined miscibility gap boundary is quasi-binary at a given Cu concentration, which is located between the corresponding binodals of the boundary systems Cu–Co and Cu–Fe. The liquid phase separation temperature determined directly and reproducibly from the onset temperature of the differential thermal analysis (DTA) traces, decreases monotonically with the increase of the Co content. Munitz et al.^[28] used electromagnetic levitation to undercool the alloys and determined the metastable phase separation temperatures by analyzing the compositions of the two separated liquids by EDS after solidification. Curiotto et al.^[29] measured the demixing temperatures of several selected Cu–Co–Fe alloys with different compositions by differential scanning calorimetry. Zhao et al.^[30] investigated the solidification behavior of gas-atomized powders of a Cu–Co–Fe alloy.

Although the immiscibility of Cu–Co–Fe ternary system can be approximately treated as a Cu–(Fe, Co) quasi-binary system according to previous studies, the liquid phase separation and solidification behaviors are significantly dependent on the Cu–Co and Cu–Fe binary systems for the ternary alloys with high content of (Fe,Co). The phase separation product compositions and microstructures under different conditions are more complicated. It is very important to explore the formation of the minor liquid phase at the initial stage of separation and subsequent coalescence and migration processes. Is there any nucleation or is the process just a spinodal decomposition? How can the two phases exchange the three chemical elements so rapidly? These processes involve complex thermodynamics, kinetics, atomic diffusion, fluid migration, and convection. So far, however, little quantitative information has been available on the metastable liquid phase separation and rapid solidification of Fe–Co–Cu alloys with high (Fe,Co) concentration under different conditions, such as cooling rate, undercooling level, and container. Especially, no work has reported quantitative measurement of (Fe,Co) dendrite growth velocity at various undercooling levels.

In the present work, we employed differential thermal analysis method in combination with glass fluxing technique to characterize the metastable phase transformation of Co₄₀Fe₄₀Cu₂₀ ternary alloy. The dendritic growth velocity of (Fe,Co) phase was measured as a function of undercooling by the electromagnetic levitation technique. The effect of undercooling level, cooling rate, convection, surface tension difference, and container state on the microstructure formation of Co₄₀Fe₄₀Cu₂₀ alloy has been demonstrated.

The alloy samples were prepared by alloying highly pure Cu (99.999%), Co (99.998%), and Fe (99.99%) in an arc-melting furnace. They were remelted several times to achieve sufficient homogeneity. The samples were within 0.25–0.35 g in mass for DTA measurement and 1–1.2 g for electromagnetic levitation. For the DTA measurement, each sample was contained in an alumina crucible covered with crushed Duran glass as a denucleant and fluxing agent and was then placed in a differential thermal analyzer (Netzsch DTA 404 S). The sample was heated up to a temperature between 1700 K and 1800 K. After an isothermal period of 10 min, the sample was cooled at a constant rate down to 600 K. 2–4 heating and cooling cycles were performed for each sample at rates of +10 K/min and −20 K/min, respectively. Soak periods of 10 min at the maximum temperature were inserted to recover homogeneity of the melt after liquid demixing and macroscopic phase separation. The melting points of pure Ag, pure Cu, and pure Ni were used to calibrate the temperature scale of the facility to an accuracy of better than ±1.5 K.

The rapid solidification and dendritic growth velocity measurement at various undercooling levels were accomplished by using the electromagnetic levitation technique. The chamber of the EML facility was evacuated to better than 5.0 × 10⁻⁶ Pa and then backfilled with a He–8 vol.% H₂ mixture. The specimen was heated above the liquidus temperature and subsequently cooled by a He–8 vol.% H₂ gas flow. A two-color pyrometer with a time resolution of 10 μs was employed to measure the temperature of the sample from the top throughout the experiment with a relative accuracy of ±3 K at a sampling rate of 100 Hz, where the emissivity was calibrated to reproduce the liquidus temperature. At the desired undercooling, solidification was started by triggering the lower end of the levitated droplet with the boron nitride sample holder. The recalescence time during solidification was measured by a specially designed fast responding photodiode infrared device, where the two photodiodes were put to be parallel to the vertical axis of the sample. Both the pyrometer and photodiode signals were simultaneously recorded by a transient-signal memory recorder. The sampling rate used for the transient recorder was 1 MHz. The dendritic growth velocity can be obtained on the basis of the photodiode signals.^[31] The phase constitutions of the solidified samples were examined by an X’pert Philips x-ray diffractometer using a Cu K_α radiation. The structures and concentration profiles were analyzed by means of a ZEISS SUPRA55 field emission scanning electron microscope (SEM) with an INCA E350 energy dispersive spectrometer under accelerating voltage of 15 kV.

Figure 1 exhibits typical DTA curves of one heating and two cooling segments of a Co₄₀Fe₄₀Cu₂₀ alloy sample. On the basis of the vertical section (Fe:Co = 1:1) of the Fe–Co–Cu ternary phase diagram,^[26] the particular phase transformation temperatures can be determined. On the heating curve in Fig. 1(a), the bcc α−(Fe,Co)→fcc γ−(Fe,Co) allotropic transition temperature T(α − γ) is determined to be 1214 K, the melting temperature of the Cu-rich solid solution T_m(Cu) = 1371 K, and the liquidus temperature T_L = 1696 K. The thermal information on metastable liquid phase separation is revealed by the DTA cooling traces, where the demixing is manifested as a small step in exothermic direction, as presented in Figs. 1(b) and 1(c). We designate the characteristic onset temperature of this process as T_sep, which is identified to be the same temperature of 1522 K for both runs. Thus, the criticla undercooling for the metatable liquid phase separation ΔT_sep = T_L − T_sep = 174 K. After the onset of liquid phase separation, the DTA signal retains its exothermic offset during further cooling. This shows that the concentration change in both separated phases continues until the rapid solidification of the (Fe,Co)-rich liquid occurs. The (Fe,Co)-rich liquid solidified at 1419 K and 1417 K for the two cooling runs, respectively. Subsequently, the peritectic transformation took place at the same temperature, T_s(Cu) = 1369 K, for both cooling segments. The subsequent γ−(Fe,Co)→α−(Fe,Co) allotropic transition occurs at T(α − α) = 1169 K and the disorder to order transformation in the α−(Fe,Co) phase at T(α − α′) = 995 K. The peritectic transformation undergoes a very small undercooling of 2 K. In contrast, the γ−(Fe,Co)→α−(Fe,Co) allotropic transition exhibits an undercooling of 45 K.

Fig. 1.

	Figure Option ViewDownloadNew Window
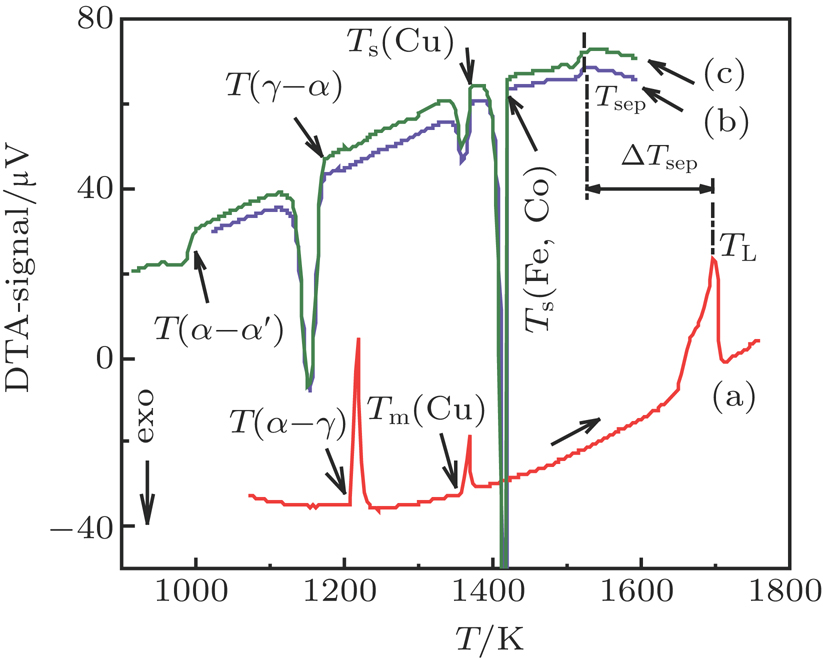	Fig. 1. (color online) DTA traces of heating and cooling for a Co40Fe40Cu20 sample: (a) one heating segment; (b) and (c) two cooling segments.

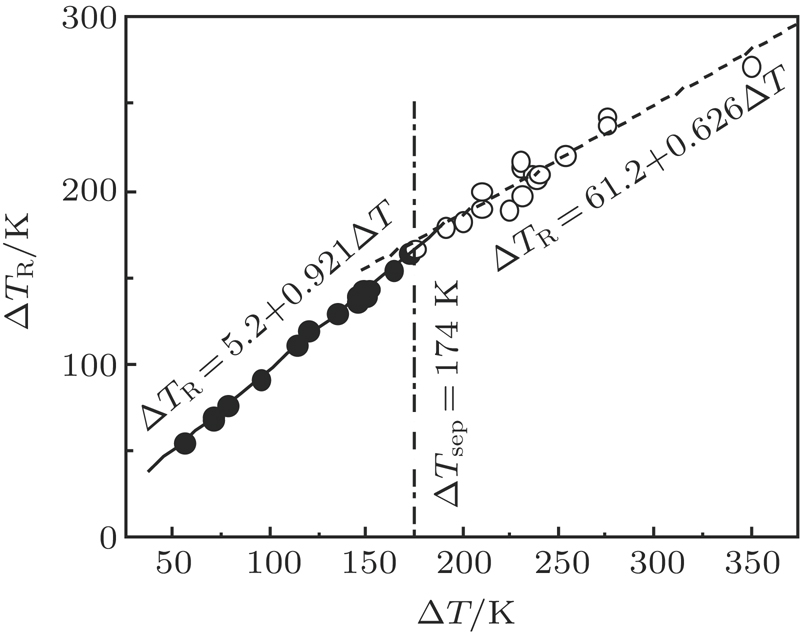
Figure 2 shows the structural morphologies of the DTA sample of Co₄₀Fe₄₀Cu₂₀ alloy solidified at 1417 K (ΔT = T_L − T_s(Fe,Co) = 279 K). Here we designate the difference between the liquidus temperature of the alloy and the initial solidification temperature as undercooling, although the real liquidus temperature of the (Fe,Co)-rich liquid should be higher than that of the nominal alloy. Obviously, a severe macrosegregation pattern has been formed, as presented in Fig. 2(a). The (Fe,Co)-rich liquid phase was completely coagulated into a large sphere before solidification, occupying the most volume of the sample. Although the volume fraction of the Cu-rich phase is small, most of the Cu-rich phase is distributed at the outer surface of the sample except for some small Cu-rich spherulites embedded inside the (Fe,Co)-rich phase. It can be deduced that the Cu-rich liquid has a stronger ability of wetting the molten glass and smaller surface tension than the (Fe,Co)-rich liquid, resulting in the migration of the Cu-rich liquid towards the sample surface under the condition of low cooling rate. However, the Cu-rich phase is convex lens shaped, instead of spherical, indicating that the Cu-rich liquid wets the solidified (Fe,Co)-rich phase well under the condition of molten Duran glass covering the sample completely. Figure 2(b) illustrates the microstructure of the solidified (Fe,Co)-rich liquid. The (Fe,Co)-rich phase grains with different colors were formed due to different orientations. Many Cu-rich spheres with diameter up to 2 μm are dispersed in the matrix of (Fe,Co)-rich phase and Cu-rich phase layers distribute at the grain boundaries. This implies that the liquid phase separation process did not finish until solidification occurred. EDX shows that the average composition of the (Fe,Co)-rich sphere is 44.63 at.% Fe, 43.63 at.% Co, and 12.74 at.% Cu, which should be the composition of the large (Fe,Co)-rich drop at the moment of formation by coalescence.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Structural morphologies of the DTA sample of Co40Fe40Cu20 alloy solidified at an undercooling of 279 K: (a) overview of the vertical section; (b) microstructure of the solidified (Fe,Co)-rich liquid.

By using EML technique, undercooling up to 345 K has been achieved for Co₄₀Fe₄₀Cu₂₀ alloy. Figure 3 presents the temperature-time profiles measured by a pyrometer on one bulk sample containerlessly processed by EML and undercooled by 83 K, 145 K, 174 K, and 248 K, respectively. The cooling rate is about 10–30 K/s and it is found that the cooling rate has no significant effect on undercooling level achieved during electromagnetic levitation. According to the measurement of DTA, the critical undercooling for metastable immiscibility for this alloy is 174 K. However, no evident indication of liquid phase separation has been observed on the cooling curves. Once the (Fe,Co)-rich liquid phase nucleates, sharp recalescence takes place and brings on a temperature rise, which is designated as ΔT_R. The relationship between recalescence induced temperature rise ΔT_R and undercooling level ΔT is shown in Fig. 4. As undercooling increases, the temperature rise linearly increases because of the enhancement of recalescence. It is apparent that the slope of the ΔT_R–ΔT function in the case of occurrence of demixing is smaller than that in the case of solidification occurring above the critical demixing temperature. The origin of this difference, however, needs further investigations.

Fig. 3.

	Figure Option ViewDownloadNew Window
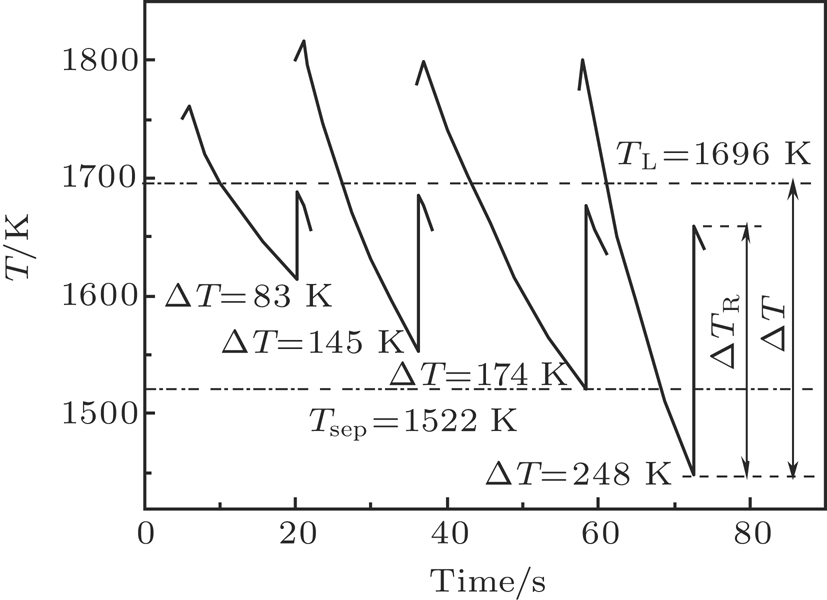	Fig. 3. Illustration of recorded recalescence events of Co40Fe40Cu20 alloy from the pyrometer signals during electromagnetic levitation processing.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Recalescence temperature rise of Co40 Fe40Cu20 alloy versus undercooling.

The x-ray diffraction patterns of Co₄₀Fe₄₀Cu₂₀ samples solidified during DTA measurement and EML processing are illustrated in Fig. 5. In all the cases, bcc α−(Fe,Co) and fcc (Cu) phases are formed. No fcc γ−(Fe,Co) phase has been detected in all the samples processed by EML. It is interesting that at the undercooling of 210 K, two weak peaks are visible at 38.4° and 78.2°, respectively, as denoted by the arrows in Fig. 5. However, these two peaks do not match any phases in current database.

Fig. 5.

	Figure Option ViewDownloadNew Window
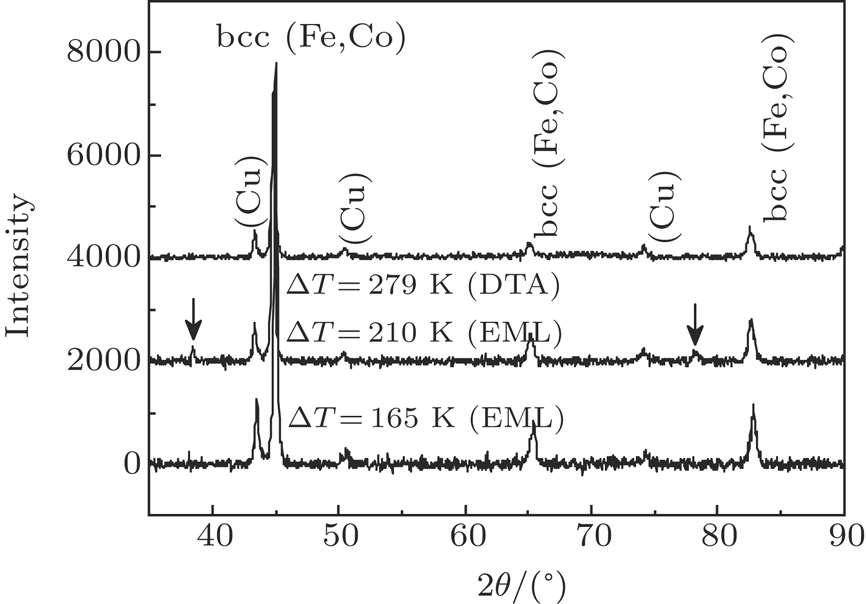	Fig. 5. X-ray diffraction patterns of Co40Fe40Cu20 samples solidified during DTA measurement and EML processing.

Figure 6 shows the microstructures of the Co₄₀Fe₄₀Cu₂₀ samples solidified at various undercoolings during electromagnetic levitation. Coarse α−(Fe,Co) dendrites are formed and the (Cu) phase is distributed interdendritically at an undercooling of 105 K (Fig. 6(a)). When undercooling reaches 165 K, the α−(Fe,Co) dendrites are drastically refined, as shown in Fig. 6(b). Figure 6 (c) presents a microstructure with phase separation (ΔT = 210 K), where Cu-rich spheres are formed in the matrix of α−(Fe,Co) phase. It is found from the vertical section of the sample that almost all the Cu-rich droplets are congregated at the upper part of the sample, without Cu-rich phase covering the sample surface. It can be inferred that the congregation of the minority phase, Cu-rich liquid, is mainly driven by the electromagnetic stirring force. However, the cooling rate during EML processing is much higher than that in DTA measurements and hence, there is not enough time for the Cu-rich droplets to come out to the sample surface before solidification occurs to the (Fe,Co)-rich liquid. The solidified (Fe,Co)-rich liquid is characterized by very fine α−(Fe,Co) grains with some (Cu) phase at grain boundaries, as shown in the inset to Fig. 6(c). After the occurrence of metastable liquid phase separation, this separation process will continue with the decrease of temperature and the compositions of the two separated liquids change along the immiscibility gap boundary. This causes the (Fe,Co)-rich liquid to be inhomogeneous during further cooling, and therefore, segregation of (Cu) phase can be observed on the grain boundaries of the (Fe,Co)-rich matrix even the solidification undercooling reaches 210 K. The diameter of the Cu-rich spheres attains several hundred microns and very coarse α−(Fe,Co) dendrites are formed inside the Cu-rich spheres (Figs. 6(c) and (d)). After liquid phase separation, the two liquids with distinct compositions are solidified in different paths. The (Fe,Co)-rich liquid solidifies at a very high velocity and forms a microstructure with fine equiaxed grains. Meanwhile, inside the Cu-rich liquid (Fe,Co) phase preferentially grows radially from the interface between the (Cu)-rich liquid and (Fe,Co)-rich solid at a very low velocity, as shown in Fig. 6(d). It is the great disparity in solidification temperature range that leads to different solidification modes in the two separated liquids.^[32]

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Microstructures of the Co40Fe40Cu20 samples solidified at various undercoolings by electromagnetic levitation processing: (a) ΔT = 105 K; (b) ΔT = 165 K; (c) ΔT = 210 K, the inset shows the microstructure of the solidified (Fe,Co)-rich liquid; (d) ΔT = 210 K, microstructure of the solidified Cu-rich liquid.

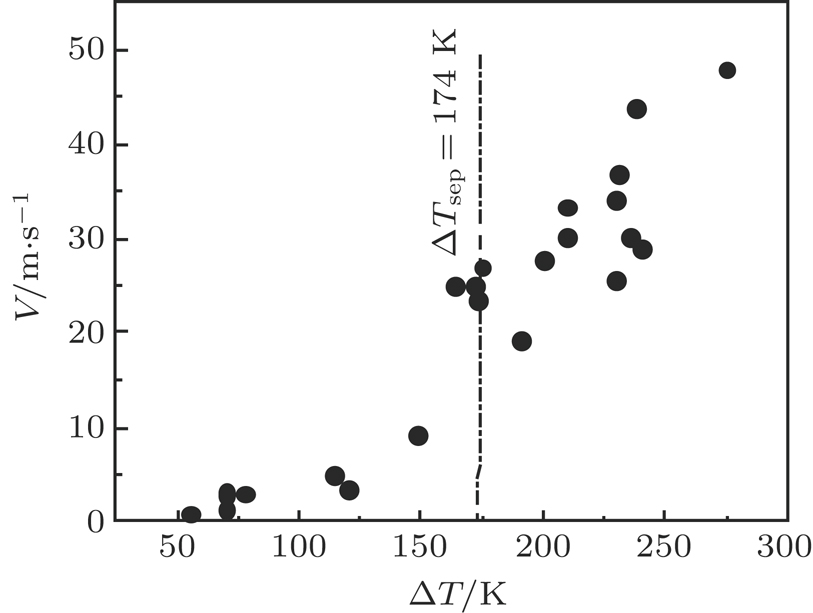
Experimental measurement of dendritic growth velocity of (Fe,Co) phase in Co₄₀Cu₂₀Fe₄₀ alloys has been carried out at different undercoolings. The dendritic growth velocity, V, as a function of undercooling is shown in Fig. 7. The dendritic growth velocity of (Fe,Co) phase increases with the enhancement of undercooling. At a certain undercooling, the growth velocity of this alloy is smaller than that of Co–Cu alloy but larger than that of Fe–Cu alloy with similar Cu concentration.^[32] When undercooling exceeds ΔT_sep = 174 K, metastable liquid phase separation results in scattering of the measured data. The (Fe,Co)-rich liquid resulting from metastable demixing beyond the critical undercooling is richer in Fe and Co than the homogeneous master alloy melt. As a result, the actual solidification undercooling of the (Fe,Co)-rich liquid phase is higher than the nominal undercooling, which is derived from the liquidus temperature of the master alloy. On the other hand, the Cu-rich liquid distributes probably in different patterns during different cooling runs even if at the same undercooling level. Consequently, the measured values of (Fe,Co) dendrite growth velocity in the case of liquid phase separation inevitably deviate from the intrinsic solidification feature of the nominal alloy.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Measured (Fe,Co) dendrite growth velocity in Co40Fe40Cu20 alloy as a function of undercooling.

The metastable phase separation and rapid solidification of undercooled Co₄₀Fe₄₀Cu₂₀ alloy have been studied by differential thermal analysis and electromagnetic levitation containerless processing. Only bcc α−(Fe,Co) and fcc (Cu) phases are formed. It is found that the undercooling level, cooling rate, convection, and surface tension difference between the two separated phases play a dominant role in the coalescence and segregation of the separated phases. Enhanced undercooling, low cooling rate, and forced convection have the effect of facilitating the metastable phase separation and coalescence process, and the difference in surface tension of the two separated liquids leads to surface segregation of Cu-rich phase in DTA measurements. The dendritic growth velocity of (Fe,Co) phase has been measured as a function of undercooling up to 275 K. The temperature rise resulting from recalescence increases linearly with the increase of undercooling because of the enhancement of recalescence.