† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51602028), the Science and Technology Development Project of Jilin Province, China (Grant No. 20160520114JH), the Youth Science Fund of Changchun University of Science and Technology, China (Grant No. XQNJJ-2017-04), and the Natural Science Foundation of Tianjin City, China (Grant No. 13JCYBJC16400).
Using the split-step Fourier transform method, we numerically investigate the generation of breathing solitons in the propagation and interactions of Airy–Gaussian (AiG) beams in a cubic–quintic nonlinear medium in one transverse dimension. We show that the propagation of single AiG beams can generate stable breathing solitons that do not accelerate within a certain initial power range. The propagation direction of these breathing solitons can be controlled by introducing a launch angle to the incident AiG beams. When two AiG beams accelerated in opposite directions interact with each other, different breathing solitons and soliton pairs are observed by adjusting the phase shift, the beam interval, the amplitudes, and the light field distribution of the initial AiG beams.
Self-accelerating Airy beams have become the focus of many theoretical and experimental investigations[1,2] due to their possible applications in particle clearing,[3] light bullets,[4] curved plasma channel generation,[5] optical routing,[6] optical interconnects,[7] image signal transmission,[8] vacuum electron acceleration,[9] abruptly autofocusing beams,[10] and so on. In the last decade, besides their use in linear media, such beams have also been extensively researched in many nonlinear materials, such as Kerr nonlinear dielectrics,[11,12] photorefractive media,[13–16] nonlocal nonlinear media,[17] Bose–Einstein condensates,[18] metal surfaces,[19] quadratic media,[20] highly non-instantaneous cubic media,[21] and photonic crystals.[22] In particular, solitons can be generated from Airy beams because of the existence of nonlinearity,[11–15] which propagate without transverse acceleration and perform a breathing state. The interactions between Airy beams can also result in the generation of single solitons or soliton pairs.[17,23–26] More recently, such solitons have been observed experimentally in photorefractive media.[13,15]
As a generalized form of Airy beams, Airy–Gaussian (AiG) beams provide a more realistic approach to the description of Airy beams, which carry finite power and retain non-diffracting properties within a finite propagation distance, and can achieve a very good approximation in experiment.[27] So far, many researchers have theoretically and experimentally studied the propagation and interactions of AiG beams.[28–37] For example, Deng et al. investigated the propagation and properties of AiG beams in a Kerr medium,[28] quadratic-index medium,[29] strongly nonlocal nonlinear media,[30] and uniaxial crystals.[31] They also discussed the interactions of AiG beams in Kerr and saturable media.[32,33] Furthermore, Zhang reported the bound states of breathing AiG beams in a nonlocal nonlinear medium.[34] Shi et al.[35] discussed the interactions of AiG beams in photonic lattices with defects. Gao et al.[36] analyzed the radiation force functions of two AiG beams on a cylindrical particle. We also studied in detail the propagation and interactions of AiG beams in saturable nonlinear media in a recent article.[37]
However, due to strong focusing nonlinearity, unstable soliton propagation may occur in cubic media for intense excitation at the input plane.[12] So, how can we obtain stable solitons during the propagation of AiG beams? How can we control the propagation of these breathing solitons? What factors can affect the propagation and interactions of AiG beams? These questions are very interesting.
In this paper, we introduce a higher-order nonlinearity, such as the defocusing quintic type, which can suppress the strong cubic nonlinearity so as to obtain stable breathing solitons. In one transverse dimension, we first numerically study the propagation of single AiG beams in a cubic–quintic nonlinear medium, and then the stability and the propagation control of the solitons produced by the AiG beams. In addition, we briefly investigate the interactions of two AiG beams by adjusting their initial amplitudes, phase shift, beam interval, and the initial light distribution factor.
Under paraxial approximation, we consider the generalized nonlinear Schrödinger equation in the normalized one transverse dimension form[38]
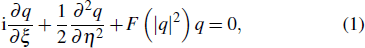 |
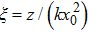
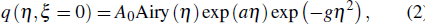 |
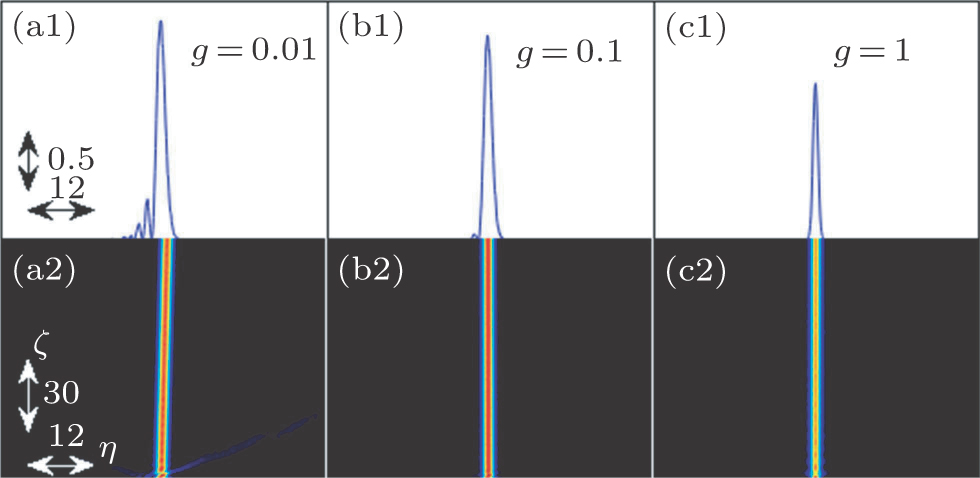
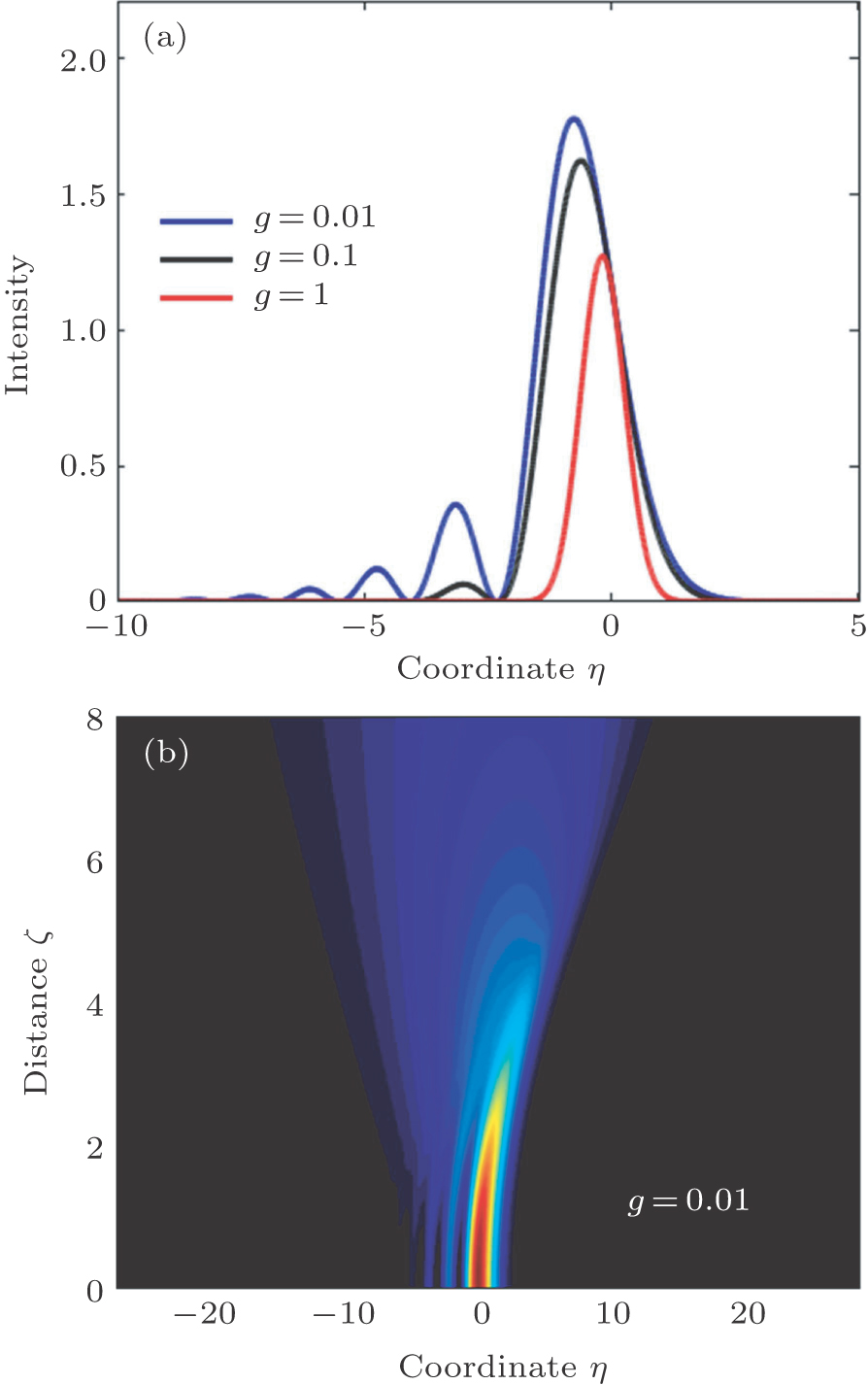 | Fig. 1. (color online) (a) Intensity distributions of AiG beams with g = 0.01, 0.1, and 1. (b) Propagation of AiG beam in free space for g = 0.01. |
We have shown the single beam solutions in Eq. (
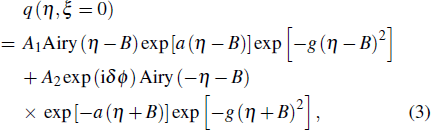 |
To investigate the propagation of a single AiG beam in a cubic–quintic nonlinear medium, we have implemented the well-known split-step Fourier transform methods to solve Eq. (
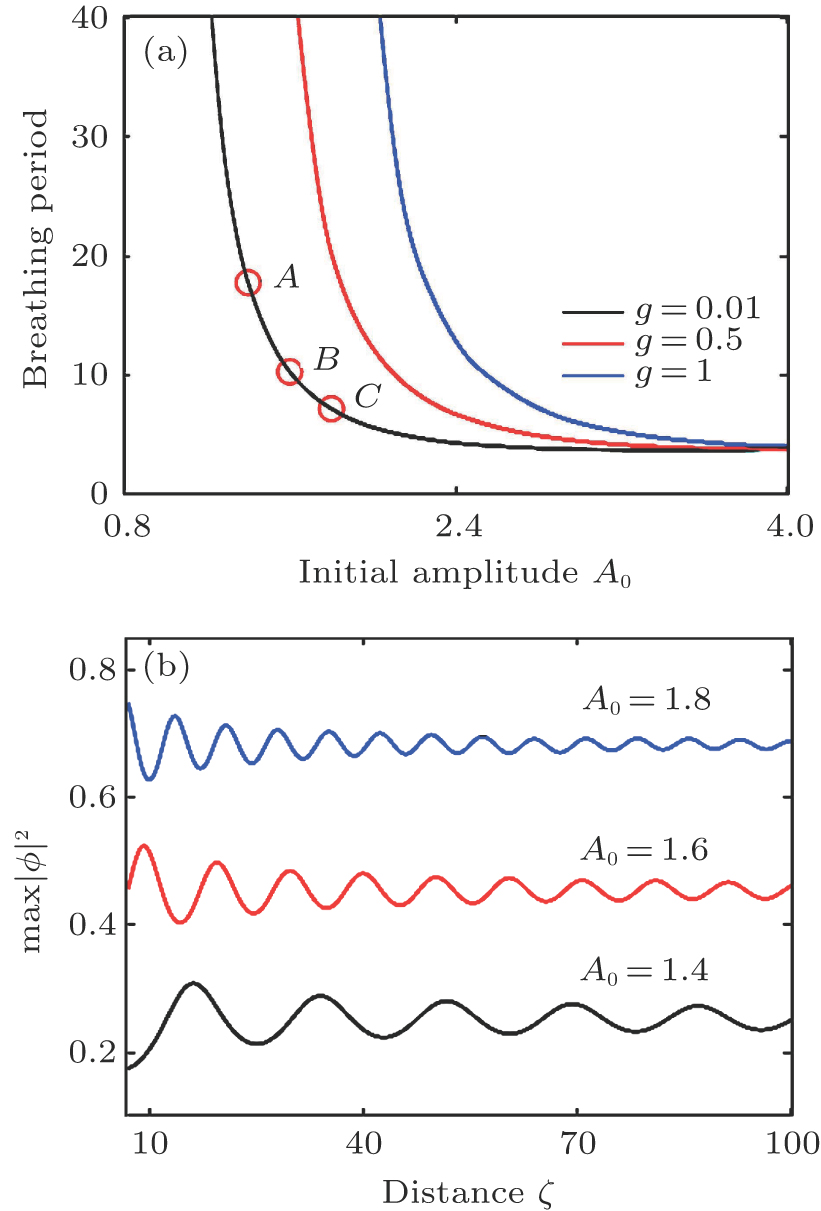
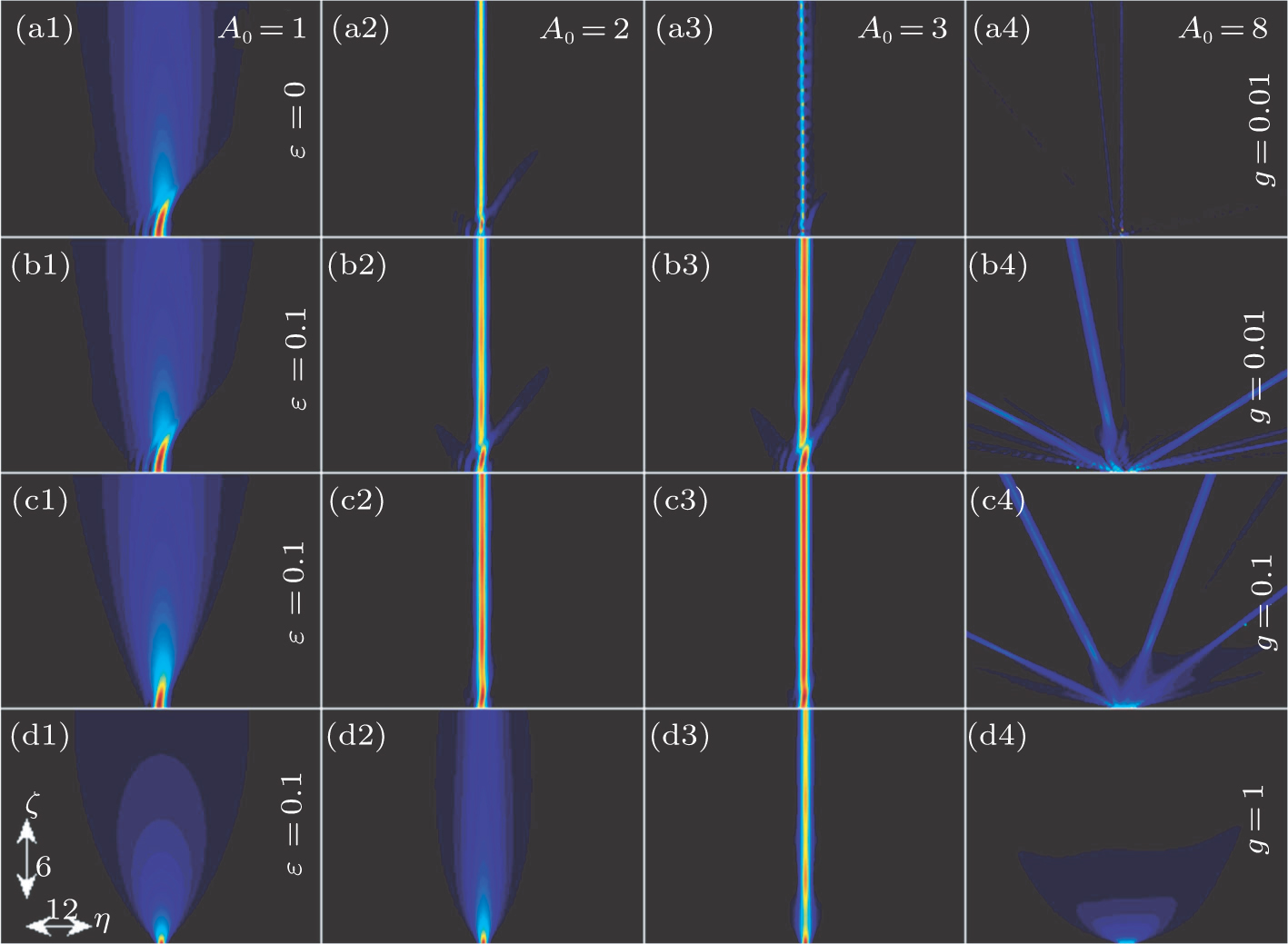 | Fig. 2. (color online) Soliton generation in the propagation of a single AiG beam in a cubic–quintic nonlinear medium with changing values of A0, g, and ε. |
In this paper, our focus is on the case of ε = − 1 where the defocusing quintic nonlinearity will weaken the focusing cubic nonlinearity, so as to strengthen the stability of the breathing soliton. As seen in Figs.
We have examined the relations between the soliton oscillations and the incident AiG beam amplitude. One can see in Fig.
To check the stability properties of these breathing solitons, we simulate their evolution under some random perturbations. As an example, figures
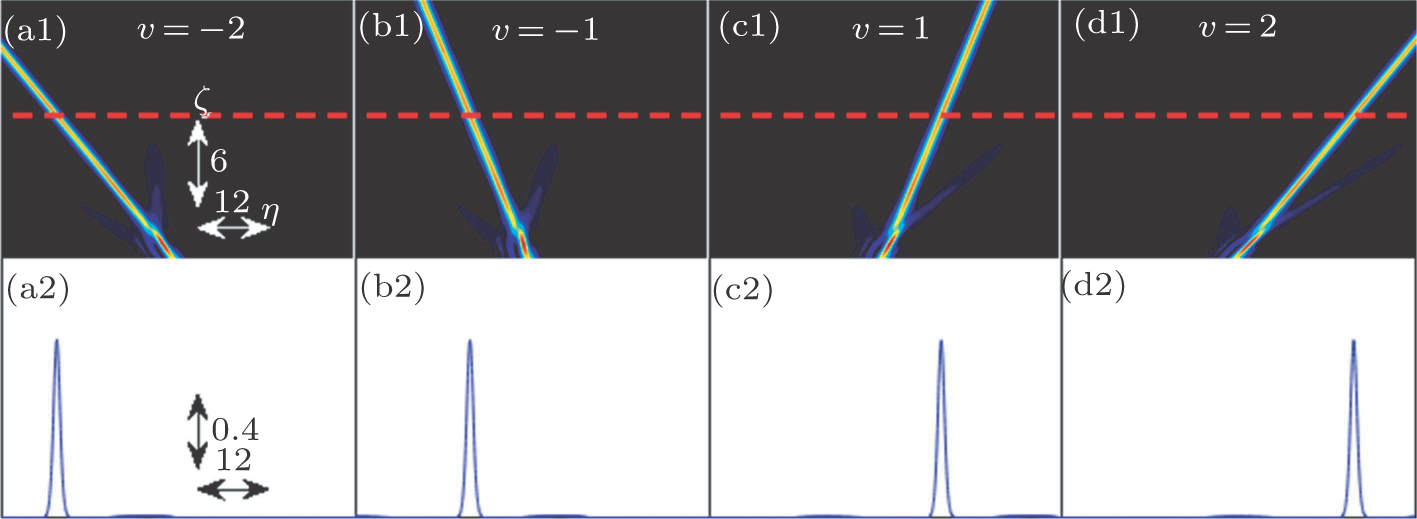
In order to control the propagation direction of the breathing soliton, we introduce a launch angle to the incident AiG beam. For computer modeling of this process, we solved Eq. (
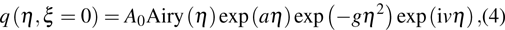 |
In Figs.
In this section, we will focus on interactions of AiG beams in a cubic–quintic nonlinear medium. The split-step Fourier method is used to solve Eq. (
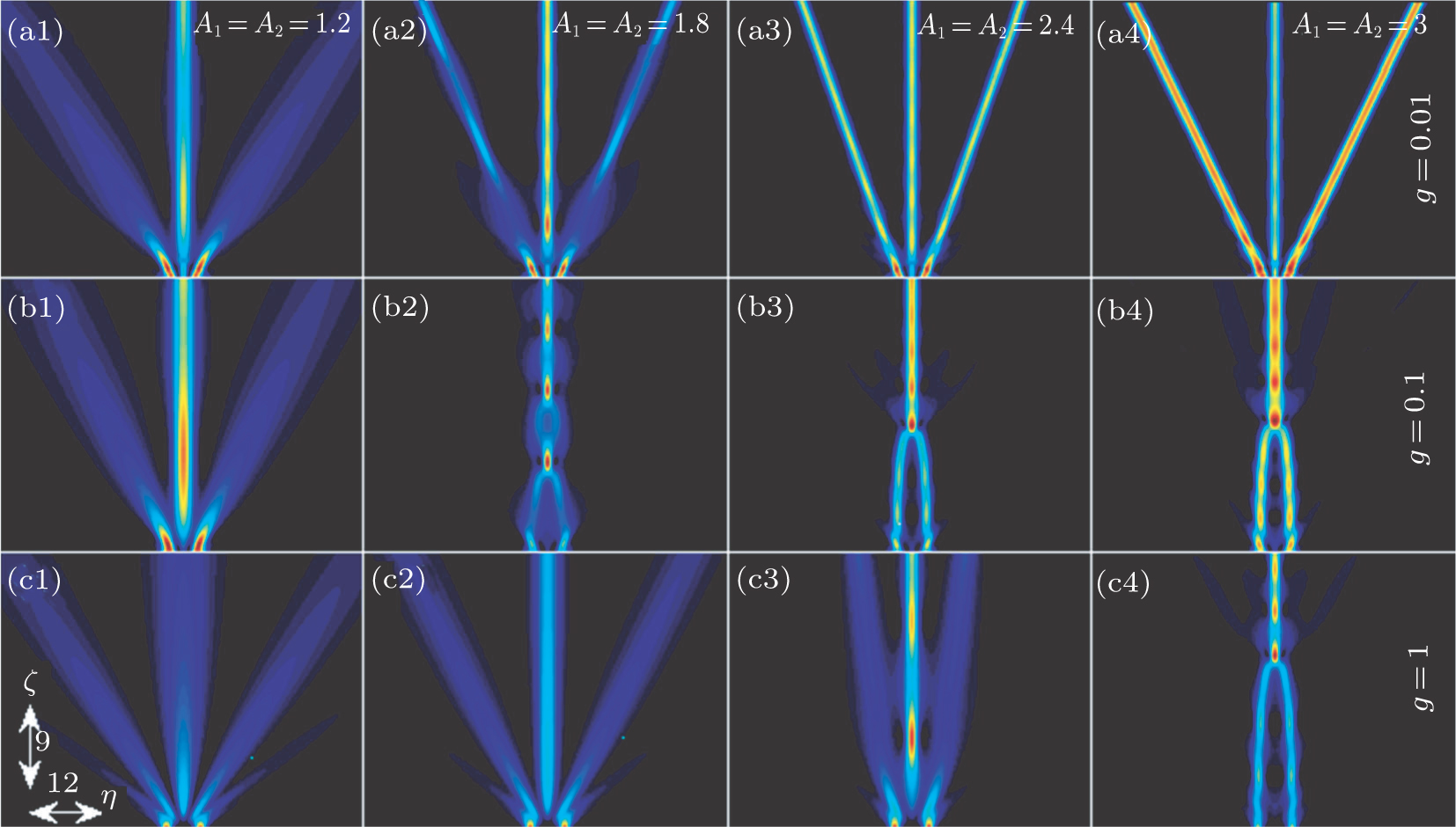
Firstly, when A1 = A2 = 1.4 and g = 0.01, numerical simulation results with different phase shifts δϕ and beam intervals B (relatively small) are depicted in Fig.
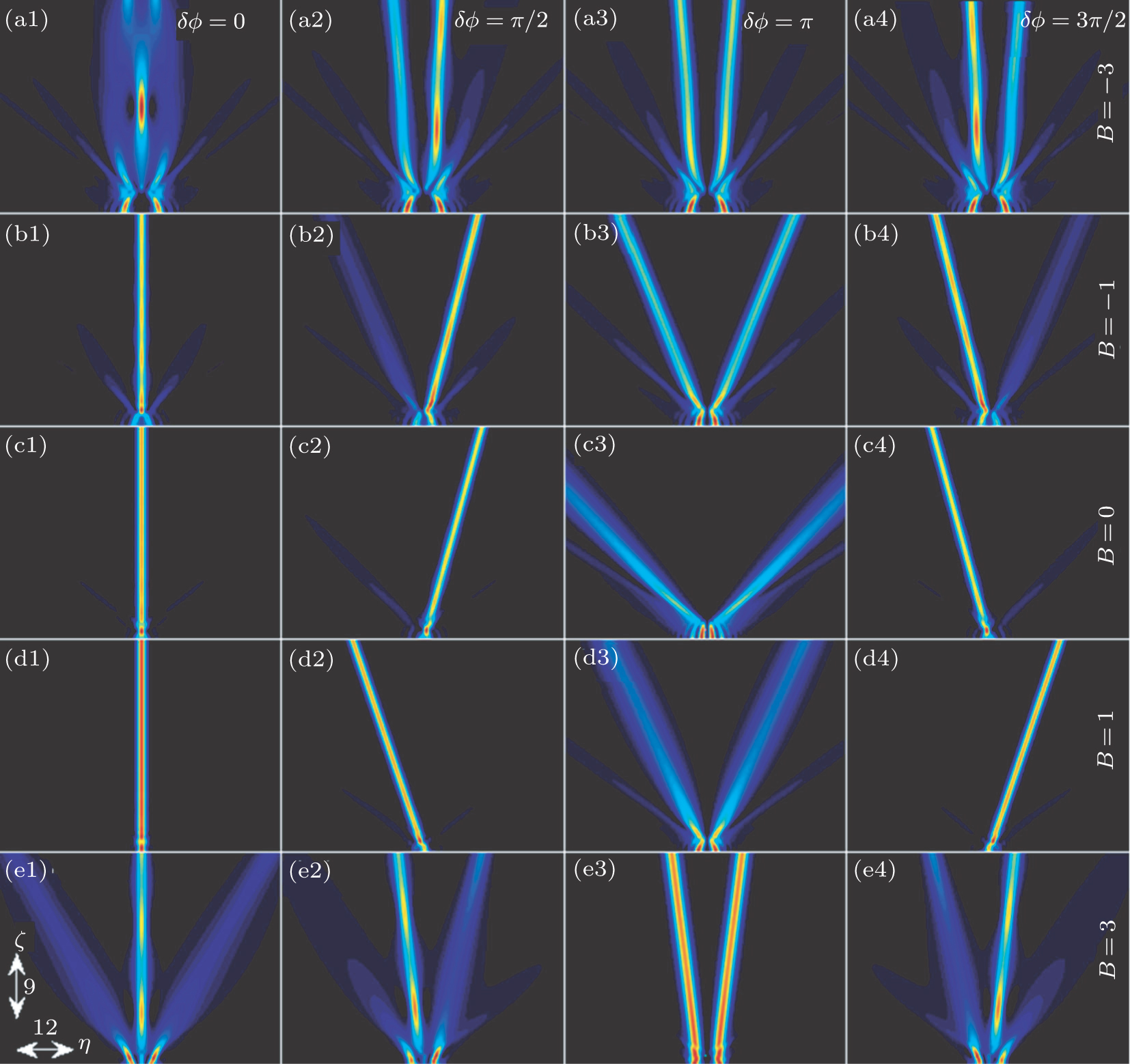 | Fig. 6. (color online) The interactions of two AiG beams with different phase shifts and beam intervals. Other parameters are A1 = A2 = 1.4 and g = 0.01. |
Secondly, as an example, for B = 3 in the in-phase case, we consider the interaction of two AiG beams for different A1 and A2 in cubic–quintic nonlinear media, as shown in Fig.
We have numerically investigated the generation of breathing solitons in the propagation and interactions of AiG beams in a cubic–quintic nonlinear medium in one transverse dimension by using the split-step Fourier transform method. We find that stable breathing solitons can be produced in the propagation of single AiG beams due to the compensation of the defocusing quintic nonlinearity on the focusing cubic nonlinearity within a certain range of the initial amplitude A0. The soliton breathing period decreases and the maximum intensity of the soliton increases monotonically with increasing A0. The propagation direction of the solitons can be adjusted by controlling the launch angle of the AiG beams. In addition, numerical simulations of the interactions between two AiG beams are carried out in a cubic–quintic nonlinear medium.The results show that different single breathing solitons or soliton pairs can be obtained by adjusting the phase shift and interval between two AiG beams for given values of the initial amplitude. When the initial amplitudes are changed, the interactions of the two AiG beams can lead to single breathing solitons and symmetrical soliton pairs when the initial light field distribution tends to be the Airy distribution. The intensity of the symmetrical soliton pair increases and the intensity of the single breathing soliton decreases with increase of the initial amplitudes. When the initial light field distribution is close to the Gaussian distribution, only single breathing solitons can form. The bigger the initial amplitudes are, the larger the soliton intensity is and the faster the soliton breathing rate is.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |