† Corresponding author. E-mail:
The controllability problem of heterogeneous interdependent group systems with undirected and directed topology is investigated in this paper. First, the interdependent model of the heterogeneous system is set up according to the difference of individual characteristics. An extended distributed protocol with the external sliding-mode control is designed, under which it is shown that a heterogeneous interdependent group system is controllable when the corresponding communication topology is controllable. Then, using the network eigenvalue method, the driving individuals are determined for a heterogeneous system with undirected topology. Under directed topology, the maximum match method is utilized to confirm the driving individuals. Some sufficient and necessary conditions are presented to assure that the heterogeneous interdependent group system is structurally controllable. Via theoretical analysis, the controllability of heterogeneous interdependent systems is related to the interdependent manner and the structure of the heterogeneous system. Numerical simulations are provided to demonstrate the effectiveness of the theoretical results.
Due to the great progress in science and technology, distributed coordinated control of group systems has been researched intensively. Many results have been acquired and applied in science and engineering fields such as spacecraft formation flying, data fusion of multi-sensors, cooperative surveillance,[1] multiple mobile robotic systems,[2–4] and so forth.[5–9]
From the control point of view, it is known that controllability is a fundamental characteristic of the structure of the system, which reflects the ability of the input to control the state of the system. For a linear control system, Lin[10] presented the concepts of structure and structural controllability, and some necessary and sufficient conditions are given. Liu et al.[11] developed analytical tools to research the controllability of several real networks. Through advisably perturbing the network structure, Wang et al.[12] proposed an approach to optimizing the controllability complex networks. Hou et al.[13] put forward a method to improve the controllability of a directed network via changing the direction of a small fraction of links. Yan et al.[14] introduced the concept of exact controllability, and achieved full control of a network based on the maximum multiplicity to confirm the minimum set of drive nodes required. Moreover, Yuan et al.[15] analyzed the exact controllability of multiplex networks, which are multiple-relation networks and multiple-layer networks, and found a small fraction of the interconnections to enhance the controllability. However, in the above research results, the interdependence of directed networks is not considered for real systems such as traffic power networks, heterogeneous multi-agent (group) systems, and so on.
For group systems, the purpose of the controllability problem is to drive all individuals achieving desired ideal states from any initial states just through several driver individuals externally. The study of the controllability of group systems is still challenging owing to more factors such as interaction topologies, control protocols, driver individuals selection, and so on. Tanner[16] put forward firstly the concept of the controllability of multi-agent systems, as well as provided an algebraic necessary and sufficient conditions of the system to be controllable by a leader. Based on that, using controllability, Ji et al.[17] studied the formation control of multi-agents networks under leader-follower structure. It is shown that the topology structure of the interconnection graph uniquely confirmed the controllability of multi-agent systems. Wang et al.[18] investigated the controllability of multi-agent systems with an undirected graph on the basic of agreement protocols. The controllability condition of high-order dynamic agents networks was provided. Parlangeli et al.[19] researched the reachability and observability properties of a network system with the communication graph of cycle or paths. On the basis of simple algebraic rules from number theory, some necessary and sufficient conditions are given. Under switching topologies, Liu et al.[20] proposed graph-theoretic characterizations of the structural controllability for multi-agent systems. Further, Yazicioglu et al.[21] studied the controllability of diffusively coupled networks from a graph theoretic perspective. More specifically, a graph topological lower bound on the rank of the controllability matrix was presented, that is applicable to systems. Ji et al.[22] put forward a neighbor-based control protocol, and showed that the communication topology determined solely the controllability of a multi-agent system from a graph theory perspective. In the above studies, most of multi-agent models are single-integrator dynamics. Liu et al.[23] investigated second-order controllability of multi-agent systems with multiple leaders. Consider the velocity coupling topology, some sufficient and necessary conditions were presented for the controllability of the system with multiple leaders. For improving the controllability of multi-agent systems, Zhao et al.[24] presented a leader selection algorithm and a weight adjustment algorithm.
From the above discussions, most of the aforementioned works mainly focus on the controllability of homogeneous multi-agent systems. Nevertheless, to the best of our knowledge, that many results are from a few works on the controllability of heterogeneous group systems. Generally speaking, the heterogeneity is common in nature and engineering systems, for instance, the different gender, occupation, interests of individuals in human social groups, and cooperative tasks of different military equipment. Guan et al.[25] studied the controllability of multi-agent systems under the leader-follower framework with directed topology. Guan et al.[26] investigated the controllability of both continuous and discrete-time linear heterogeneous multi-agent systems. However, it neglected the evolution and cooperation relationships among subsystems. Chen et al.[27,28] investigated the model of interdependent networks and the robustness of interdependent networks in cascading failures from different aspects. Inspired by the above analyses, this paper investigates the controllability problem of heterogeneous interdependent group systems under undirected and directed topology. In the present article, from the point of the difference of individual characteristics, the interdependent model of the heterogeneous group system is structured. The main contributions of the paper are summarized as follows. For heterogeneous group systems under undirected and directed topology, the corresponding methods are used to confirm the driving individuals, which are the network eigenvalue method and the maximum match method. An extended distributed protocol with the external sliding-mode control is presented. In the meantime, some sufficient and necessary conditions are given to ensure that the heterogeneous interdependent group system is structurally controllable. The interdependent manner and the structure of a heterogeneous system impact on the controllability of the heterogeneous interdependent system.
The rest of this paper is organized as follows. In Section



In a group system, the information flow between individuals is usually modeled by an interaction digraph 
























For the controllability discussion of group systems, some individuals are taken to play an individual driving role and others are ordinary individual roles. The ordinary individuals follow the neighbor-based law, but the driving individuals are free, which are allowed to arbitrarily select their control input. In such a way, the states of driving individuals are counted as inputs, which is used to control ordinary individuals.
Assume that a heterogeneous group system is made up of 







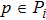


In this paper, we consider the model of a heterogeneous system with two subgroups, which have different characteristics and topology structures, as shown in Fig. 







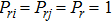
Without loss of generality, consider a heterogeneous interdependent group system with single-integrator dynamic individuals. In order to succinctly present, suppose that the states of all individuals are in a one dimensional space. The dynamics of individuals are given by









Corresponding to the partition of individuals into driving individuals and ordinary individuals, the Laplacian matrix L can be partitioned as



Under the control input (




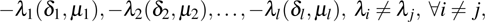







In this section, based on the model of interdependence, the controllability is discussed for the heterogeneous interdependent group system (or the corresponding communication topology) with undirected and directed topology. Consider the heterogeneous interdependent group system (
Let r denote the command signal, the position error 







In a heterogeneous group system, the system is sure to be controllable when all individuals are driven by an external control signal. In practical application, it is necessary to reduce energy consumption. Hence, the main question is how to find effectively minimum driving individuals making the group network system controllable.
The key to our theory is based on the two multiplicities and the controllability by the PBH rank condition.[29] Using the nonsingular transformation 



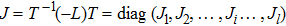







(i) Suppose that the geometric multiplicity of eigenvalue 




(ii) In transformation matrix 







Furthermore, in order to get optimal driving individuals, we use the different methods to select driving individuals for heterogeneous interdependent group systems with undirected and directed topology.
In this subsection, using the network system eigenvalue method, the driving individuals are chosen for a heterogeneous system with undirected topology. For the undirected communication topology G, the network system eigenvalue method is described as follows:
i) To obtain the Laplacian matrix L of the graph G.
ii) The eigenvalue of −L is calculated, that is 

iii) The matrix 
iv) In the column (or row) canonical form, the individuals corresponding to linearly dependent rows (or columns) are driving individuals. The number of driving individuals is equal to the algebraic multiplicity 

Consider a simple group system (n = 6) with undirected communication topology, as shown in Fig.
 | Fig. 2. (color online) A heterogeneous group system with undirected topology: (a) the communication topology and (b) the interdependent model. |
The corresponding matrix −L and eigenvalues are described as





Moreover, it is known that the proportion of interdependent individuals is 
Given a bipartite graph H, F is a subset of edge set E, namely, 



Taking into account a group system (n=7) with directed communication topology, as shown in Fig.
 | Fig. 3. (color online) A heterogeneous group system with directed topology: (a) the communication topology and (b) the corresponding bipartite graph. |
(I) The communication topology is converted to the corresponding bipartite graph for a heterogeneous group system with directed topology, as shown in Fig.
(II) Finding the maximum matching edge set of the corresponding bipartite graph Fig.

In the first group, 



From the above analysis, it is known that the number of drive node sets is two for the directed communication topology in Fig. 




It is known that there exists 










In this section, some examples are provided to further demonstrate the effectiveness of theoretical results.






By Eq. (



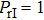










 | Fig. 6. (color online) The external control and states of individuals: (a) the external sliding-mode control    |
Similarly, when the individual 









 | Fig. 7. (color online) The external control and states of individuals: (a) the external sliding-mode control    |




To structure the transformation matrix T, T and the corresponding inverse matrix 

Using the nonsingular transformation 




Set 



 | Fig. 8. (color online) The external control and states of individuals: (a) the external sliding-mode control  |






The transformation matrix T is structured as









Set 








In this paper, the controllability problem of heterogeneous interdependent group systems with undirected and directed topology has been investigated. In the light of the difference of individual characteristics, the interdependent model of the heterogeneous system has been structured. Then, an extended distributed protocol has been proposed, which has the external sliding-mode control. For heterogeneous systems with undirected topology, the driving individuals have been confirmed by the network eigenvalue method. Under directed topology, the maximum match method has been used to identify the driving individuals. Meanwhile some sufficient and necessary conditions have been presented to ensure that the heterogeneous interdependent group system has been structurally controllable. The relationship of the interdependent manner and the controllability has been analyzed on heterogeneous systems. In addition, the effectiveness of theoretical results has been showed via numerical simulations. In the future, the controllability of high-order heterogeneous interdependent group systems can be further researched.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |












