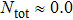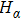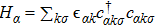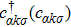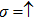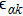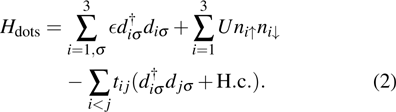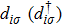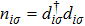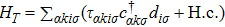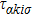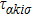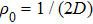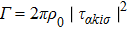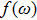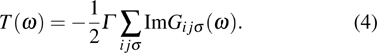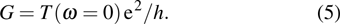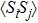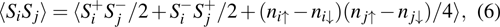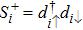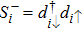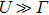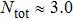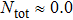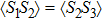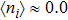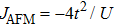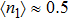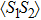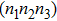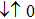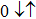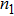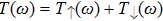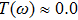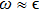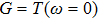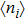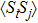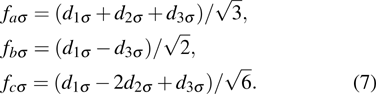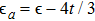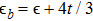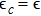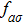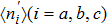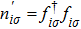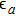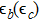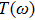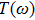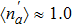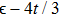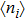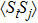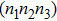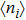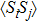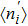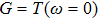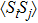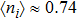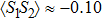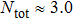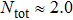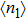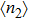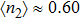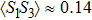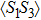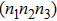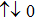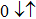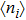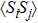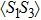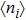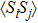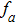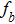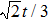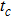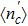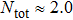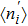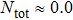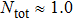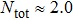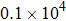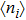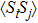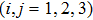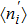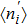1. IntroductionSemiconductor quantum dot system is considered as a promising candidate for quantum computation due to its ability to confine single electron at discrete energy levels and fine manipulation of parameter space.[1,2] During the past two decades, tremendous progress has been made in understanding the charge and spin transport for single and double quantum dot structures both in experimental and theoretical aspects.[3–9] Recently, the research interest has focused on the triple quantum dot (TQD) systems. Experimentally, TQDs are used to realize multielectron hybrid qubit,[10–13] spectral absorbers,[14,15] charge detectors,[16] and current rectifiers.[17,18] While in the theoretical field, TQD structure offers the potential to study some new fascinating phenomena at low temperatures, including the Kondo effect,[19–22] the Fermi liquid theory,[23,24] the quantum interference,[25,26] and various kinds of quantum phase transitions (QPT).[27–31]
TQD structure could be organized in serial,[32,33] parallel,[34–36] or triangular[37–40] spatial configuration, which may naturally result in different quantum behaviors. Among these configurations, the parallel TQD (PTQD) system is a basic one, which has also inspired a wealth of research. Although many works have been done related to the PTQD model, the charge transport and phase transition are less studied beyond the Kondo regime, which, in all cases, are important for the dynamic and static properties, even for the potential application in nanodevices. In this paper, we consider a PTQD device connected to two conduction leads (see Fig. 1(a)) deviated from the Kondo regime. With the usage of Wilson’s numerical renormalization group (NRG) method, we find the inter-dot hopping t may lead to some interesting quantum behaviors in the QPT and charge transport at the strongly correlated limit, quite different from the Kondo regime. More importantly, these behaviors depend closely on the initial electron number on the dots, which is usually adjusted by an external gate voltage. For instance, when the initial charge number of the dots 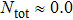 , the linear conductance G reveals a peak shape as t increases. An orbital spin-1/2 Kondo effect could be found between the conduction leads and the bonding orbital. When t is large enough, dot 1 (3) and dot 2 form a spin singlet, while dot 3 (1) is empty. In the regime
, the linear conductance G reveals a peak shape as t increases. An orbital spin-1/2 Kondo effect could be found between the conduction leads and the bonding orbital. When t is large enough, dot 1 (3) and dot 2 form a spin singlet, while dot 3 (1) is empty. In the regime  , G could be considered as a part of the above case and the quantum state is similar to the empty case as t is large enough. When the initial charge number
, G could be considered as a part of the above case and the quantum state is similar to the empty case as t is large enough. When the initial charge number  , we find the ground state is a magnetic-frustration phase and G is nearly zero when t is absent. This phase is sensitive to t, and is replaced by another mixture state even t is just
, we find the ground state is a magnetic-frustration phase and G is nearly zero when t is absent. This phase is sensitive to t, and is replaced by another mixture state even t is just  . A first order QPT could be identified both in dynamic and static physical quantities.
. A first order QPT could be identified both in dynamic and static physical quantities.
We organize the remaining sections as follows. In section 2, we present the model Hamiltonian, and the calculation formulas. In section 3, we describe the numerical result and discussion. Finally, a conclusion is given in section 4.
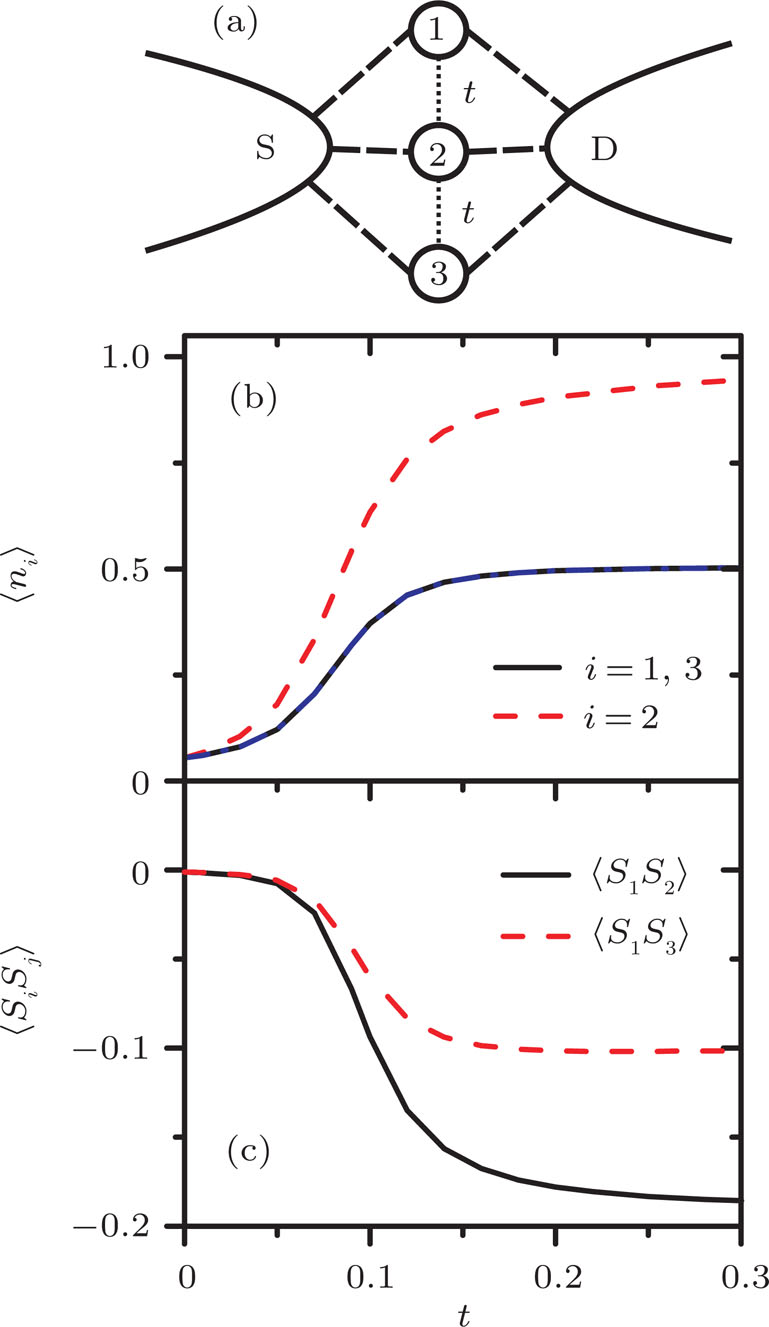
2. Model, method, and formulasThe schematic view of the PTQD structure connected to two conduction leads (source (S) and drain (D)) is presented in Fig. 1(a), and the second quantized Hamiltonian for the whole system is written as

Here,
HS and
HD correspond to the noninteracting source and drain leads respectively with
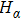
(
α = S, D):
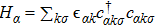
, where
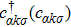
is the creation (annihilation) operator for an electron with wave vector
k, spin
σ (
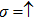
or

) in lead
α, and
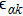
denotes the single-electron energy.
Hdots describes the energy of the PTQD:
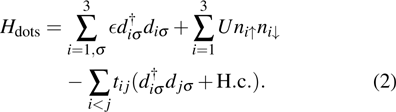
Here,
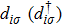
is the annihilation (creation) operator for the electrons on dot site
i (
i = 1, 2, 3).
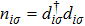
is the number operator.
ϵ and
U are the energy level and the intra-orbital Coulomb repulsion respectively, while

describes the inter-dot hopping between dots
i and
j. To avoid too many parameters, we choose

. Finally, the last term in Eq. (
1) illustrates the tunneling coupling between conduction bands and dot levels:
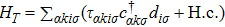
. Here,
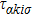
describe the couplings of the

electron states belonging to lead
α to the
i-th dot site. We assume
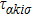
is symmetric with respect to the source and drain leads.
In the present work, we are mainly interested in the QPT and the charge transport of the PTQD device in the strong correlation regime, thus a sophisticated many-body technique must be used. Therefore, we use the NRG method,[41–43] to solve Eq. (1), which is an ideal technique to calculate both static and dynamical properties of the Anderson-type model. We first choose a constant density of states for the conduction leads 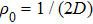 , with 2D being the band width, and D is chosen as the energy unit in the following discussions. We also approximate a constant hybridization strength between the conduction band and quantum dots
, with 2D being the band width, and D is chosen as the energy unit in the following discussions. We also approximate a constant hybridization strength between the conduction band and quantum dots 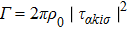 . In our NRG calculation, Λ, the renormalization parameter, is set to be 1.8 ∼2.4, and the number of the low-lying energy states kept at each iteration is about 3000.
. In our NRG calculation, Λ, the renormalization parameter, is set to be 1.8 ∼2.4, and the number of the low-lying energy states kept at each iteration is about 3000.
The linear conductance through the PTQD G is calculated by the Meir–Wingreen’s formula[44]

where
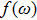
is the Fermi function, and
T(
ω) is the transmission coefficient, which is defined as
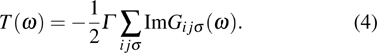
Here,

is related to the retarded dot Green’s function

, and the Fermi function is chosen as

, hence the linear conductance at zero temperature in the limit of zero bias can be written as
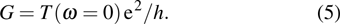
The spin–spin correlation between dots i and j is labeled as 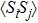 , which could be calculated as follows in the NRG steps:
, which could be calculated as follows in the NRG steps:
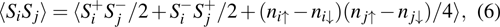
with
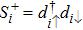
and
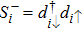
.
3. Results and discussionsIn the following discussion, we fix Γ = 0.01 and U = 0.1. Since 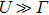 , the electron–electron interaction on the PTQD becomes significantly important, and the system is in the strong correlation limit. When ϵ sweeps downwards, the total electron number on the dots
, the electron–electron interaction on the PTQD becomes significantly important, and the system is in the strong correlation limit. When ϵ sweeps downwards, the total electron number on the dots  increases from empty to full, i.e.,
increases from empty to full, i.e.,  to 6.0. In the regime of
to 6.0. In the regime of 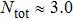 , three dots are singly occupied due to strong U, and a spin-3/2 Kondo effect could be found, resulting from the process of a local spin magnitude 1/2 is screened by the conduction leads. Thus this regime is considered as the Kondo regime,[45] which has inspired a wealth of research in the past decade. Since the effect of the inter-dot hopping t in this regime is referred by some previous works,[27] here we focus our attention on the QPT and charge transport affected by t deviate the Kondo regime.
, three dots are singly occupied due to strong U, and a spin-3/2 Kondo effect could be found, resulting from the process of a local spin magnitude 1/2 is screened by the conduction leads. Thus this regime is considered as the Kondo regime,[45] which has inspired a wealth of research in the past decade. Since the effect of the inter-dot hopping t in this regime is referred by some previous works,[27] here we focus our attention on the QPT and charge transport affected by t deviate the Kondo regime.
3.1. Effect of t in the empty regimeLet us start our discussion when the quantum dot energy level ϵ is set to be in the unoccupied regime with 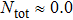 . In Figs. 1(b)–1(c), we show the electron number
. In Figs. 1(b)–1(c), we show the electron number  on each dot, and the spin–spin correlation
on each dot, and the spin–spin correlation  between dots i and j at zero temperature as functions of t with fixed ϵ = 0.1. Here,
between dots i and j at zero temperature as functions of t with fixed ϵ = 0.1. Here,  and
and 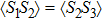 when t sweeps, since dots 1 and 3 are identical. When t = 0, one may see
when t sweeps, since dots 1 and 3 are identical. When t = 0, one may see 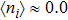 and
and  , since the PTQD is in the frozen-impurity fixed point with no residual spin. With increasing t, the charge number on each dot grows continuously, and
, since the PTQD is in the frozen-impurity fixed point with no residual spin. With increasing t, the charge number on each dot grows continuously, and  decreases to negative. Because a negative t term in Eq. (2) reduces the total energy of the system, and favors an antiferromagnetic spin arrangement between neighboring dots with an effective strength
decreases to negative. Because a negative t term in Eq. (2) reduces the total energy of the system, and favors an antiferromagnetic spin arrangement between neighboring dots with an effective strength 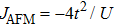 . When t is large enough,
. When t is large enough, 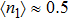 , and
, and  , illustrating that dot 2 is occupied by a single electron, whereas only one of dots 1 and 3 is singly occupied, and the other one is empty. In this case,
, illustrating that dot 2 is occupied by a single electron, whereas only one of dots 1 and 3 is singly occupied, and the other one is empty. In this case, 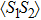 reaches to about −0.2, showing a spin singlet between dots 1 (3) and 2 is generated. Therefore, the many-body state of
reaches to about −0.2, showing a spin singlet between dots 1 (3) and 2 is generated. Therefore, the many-body state of 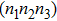 mainly includes configurations
mainly includes configurations  (or (
(or (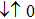 )) and (
)) and ( ) (or (
) (or (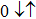 )), where dot 3 (1) is empty, while dots 1 (3) and 2 are singly occupied with antiparallel spin ordering. Here, it is notable that
)), where dot 3 (1) is empty, while dots 1 (3) and 2 are singly occupied with antiparallel spin ordering. Here, it is notable that  could not reach −0.75 of the ideal spin singlet, because the expected value of
could not reach −0.75 of the ideal spin singlet, because the expected value of 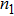 is unequal to 1.0. Besides, one also finds
is unequal to 1.0. Besides, one also finds  reaches to a larger negative value of −0.1, which can be attributed to the fact that in this regime, the Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions mediated by both the Kondo coupling between the leads and the dots and the inter-dot hopping t, which favor singly occupied states and parallel spin arrangement between different dots, become invalid. Therefore, in order to avoid the intra-orbital Coulomb repulsion and reduce the total energy, there are still some possibilities of dots 1 and 3 to form a negative spin–spin correlation. This behavior is similar to the case where the energy level goes through the intermediate valence regime in multi-quantum dot systems.[45–48]
reaches to a larger negative value of −0.1, which can be attributed to the fact that in this regime, the Ruderman–Kittel–Kasuya–Yosida (RKKY) interactions mediated by both the Kondo coupling between the leads and the dots and the inter-dot hopping t, which favor singly occupied states and parallel spin arrangement between different dots, become invalid. Therefore, in order to avoid the intra-orbital Coulomb repulsion and reduce the total energy, there are still some possibilities of dots 1 and 3 to form a negative spin–spin correlation. This behavior is similar to the case where the energy level goes through the intermediate valence regime in multi-quantum dot systems.[45–48]
Now we study the charge transport through the PTQD. In Fig. 2(a), we depict the transmission coefficient 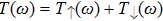 at zero temperature in terms of different t. When t = 0,
at zero temperature in terms of different t. When t = 0, 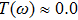 , suggesting zero conductance (see Fig. 2(b)). The spectral weight of T(ω) locates in the regime
, suggesting zero conductance (see Fig. 2(b)). The spectral weight of T(ω) locates in the regime  , and a large peak is found at energy
, and a large peak is found at energy 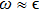 , which corresponds to the process of adding an electron on the bonding orbital as discussed in the following. With increasing t, the spectral weight moves to the direction
, which corresponds to the process of adding an electron on the bonding orbital as discussed in the following. With increasing t, the spectral weight moves to the direction  . In this process, the conductance
. In this process, the conductance 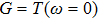 increases and reaches to its unitary limit of 1.0 at about t = 0.075. When t is large enough, the spectral weight locates in
increases and reaches to its unitary limit of 1.0 at about t = 0.075. When t is large enough, the spectral weight locates in  (e.g., t = 0.016 in Fig. 3(a)), and the conductance G decreases to 0.0 gradually. In this case, the PTQD is in a local moment formation, and the conductance is suppressed by the spin singlet between dots 1 (3) and 2, similar to the double quantum dot system with strong t in the Kondo regime.[49,50]
(e.g., t = 0.016 in Fig. 3(a)), and the conductance G decreases to 0.0 gradually. In this case, the PTQD is in a local moment formation, and the conductance is suppressed by the spin singlet between dots 1 (3) and 2, similar to the double quantum dot system with strong t in the Kondo regime.[49,50]
In order to get a clear understanding of the quantum behaviors above, we invite a canonical transformation of the three dot levels:
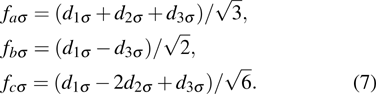
Under this transformation, the orbital levels are given by
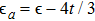
,
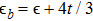
, and
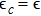
, respectively, thus
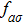
is the bonding orbital, while

and

are the anti-bonding orbitals. Besides, the

item turns out to be

, suggesting that only the bonding orbital hybridizes with the conduction leads. In Fig.
2(c), we show the electron number on the bonding and anti-bonding orbitals
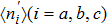
at zero temperature as functions of
t. Here,
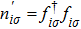
. One may see as
t increases,

keep at 0.0, while

increases gradually, since
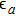
decreases with increasing
t, while
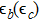
grows larger (retains at
ϵ). Correspondingly, the peak in
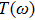
moves toward the left, for
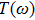
is merely decided by the local density states of the bonding orbital. When
t = 0.075,
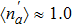
, and the present model maps to a single impurity Anderson model. An orbital spin-1/2 Kondo effect could be found between the conduction leads and the bonding orbital, and the linear conductance
G reaches to its unitary limit (Fig.
2(b)). Here, the value of
t could be estimated as follows: when the bonding orbital is singly occupied, annihilating (creating) an electron on this orbital will cost energy
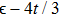
, which gives
t = 0.075, and is consistent with our NRG result. When
t is large enough, the bonding orbital is almost fully occupied, thus the electrons could not transmit the PTQD.
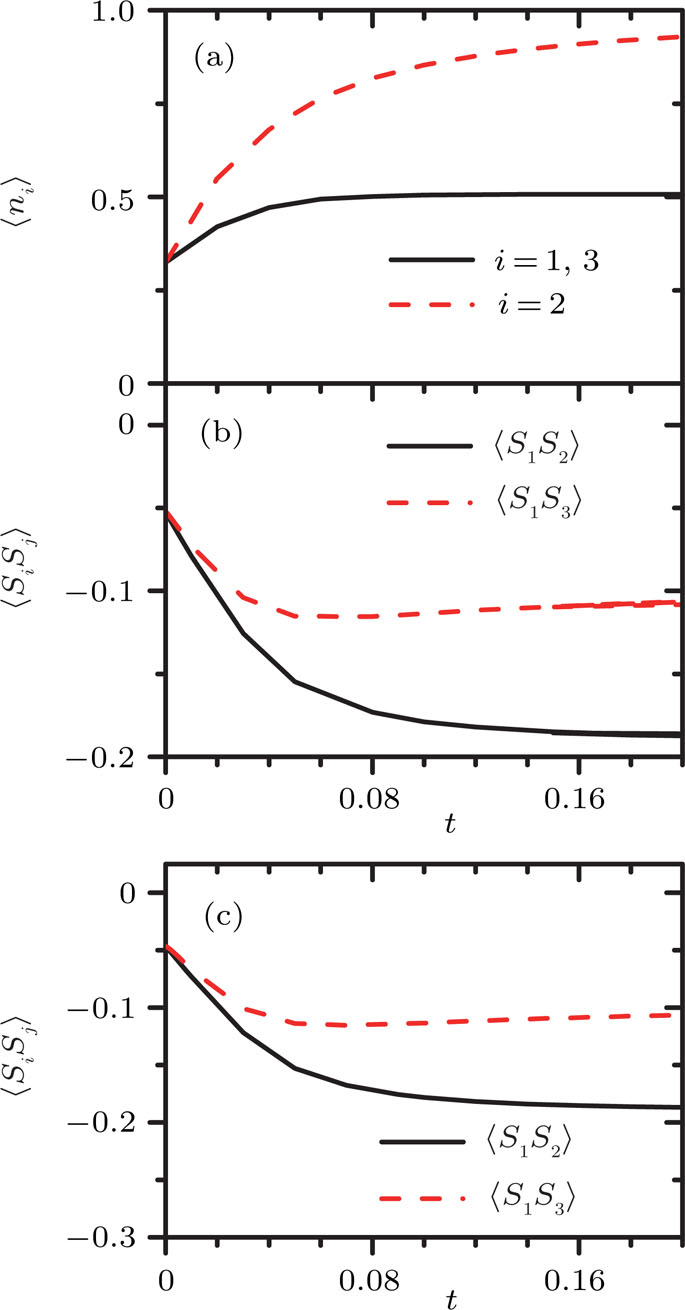
3.2. Effect of t in the singly occupied regimeNow we turn to the case when the PTQD is singly occupied with  . Figure 3(a)–3(b) show
. Figure 3(a)–3(b) show 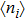 , and
, and 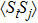 as functions of t at zero temperature for fixed ϵ = −0.004. It is seen
as functions of t at zero temperature for fixed ϵ = −0.004. It is seen  and
and  when t = 0, indicating the many-body state of
when t = 0, indicating the many-body state of 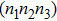 mainly includes configurations such as (1 0 0), (0 1 0), and (0 0 1), where one of the dots is singly occupied while the other two are empty. With increasing t,
mainly includes configurations such as (1 0 0), (0 1 0), and (0 0 1), where one of the dots is singly occupied while the other two are empty. With increasing t, 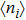 grows, while
grows, while 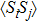 decreases continuously. When t is large enough,
decreases continuously. When t is large enough,  , while
, while  , similar to the case of ϵ = 0.1 with large t. Thus dot 1 (3) is empty, while dots 3 (1) and 2 are singly occupied with antiparallel spin ordering.
, similar to the case of ϵ = 0.1 with large t. Thus dot 1 (3) is empty, while dots 3 (1) and 2 are singly occupied with antiparallel spin ordering.
To understand the charge transport through the PTQD, we illustrate  for various t, G, and
for various t, G, and 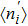 as functions of t in Figs. 4(a)–4(c), respectively. One finds
as functions of t in Figs. 4(a)–4(c), respectively. One finds 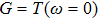 reaches to almost 1.0 of the unitary limit when t is absent. Because in this case, the charge number on the bonding orbital
reaches to almost 1.0 of the unitary limit when t is absent. Because in this case, the charge number on the bonding orbital  (Fig. 4(c)), and the orbital spin-1/2 Kondo effect could be found between the conduction leads and the bonding orbital. As t increases, the peak in
(Fig. 4(c)), and the orbital spin-1/2 Kondo effect could be found between the conduction leads and the bonding orbital. As t increases, the peak in  moves toward the left and the conductance decreases to 0.0 gradually due to decreasing
moves toward the left and the conductance decreases to 0.0 gradually due to decreasing  . In this process,
. In this process,  grows correspondingly, then stabilizes at 2.0 when t is large enough. In Fig. 3(c), we also give
grows correspondingly, then stabilizes at 2.0 when t is large enough. In Fig. 3(c), we also give 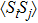 as functions of t for ϵ = −0.002. It is seen the behaviors are similar to the case of ϵ = −0.004, illustrating the discussions above are robust for the regime
as functions of t for ϵ = −0.002. It is seen the behaviors are similar to the case of ϵ = −0.004, illustrating the discussions above are robust for the regime  .
.
3.3. Effect of t in the doubly occupied regimeIn this subsection, we focus on the situation where the PTQD is doubly occupied with initial charge numer 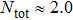 . In Figs. 5(a)–5(b), we show
. In Figs. 5(a)–5(b), we show  and
and  as functions of t with ϵ = −0.01. When t = 0, our NRG results show
as functions of t with ϵ = −0.01. When t = 0, our NRG results show 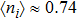 and
and 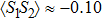 , thus two of the dots are singly occupied, while the remaining one is nearly empty. The ground state of the system is considered as a magnetic-frustration phase,[45,48] and the antiferromagnetic spin–spin correlation is resulted from the following fact: comparing with the Kondo regime where
, thus two of the dots are singly occupied, while the remaining one is nearly empty. The ground state of the system is considered as a magnetic-frustration phase,[45,48] and the antiferromagnetic spin–spin correlation is resulted from the following fact: comparing with the Kondo regime where 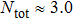 , the possibilities of each dot being singly occupied is weakened in the regime
, the possibilities of each dot being singly occupied is weakened in the regime 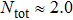 . This tendency may result in a reduction of the RKKY interaction, which is mediated by the Kondo coupling between conduction leads and quantum dots and favors parallel spin alignment between different dots. Therefore, to reduce the total energy, the local spins are more likely to form an anti-parallel spin ordering on two singly occupied dots. However, this magnetic-frustration phase is sensitive to the inter-dot coupling t, which breaks the symmetry of the three dots. As shown in Figs. 5(a) and 5(b), even t is just
. This tendency may result in a reduction of the RKKY interaction, which is mediated by the Kondo coupling between conduction leads and quantum dots and favors parallel spin alignment between different dots. Therefore, to reduce the total energy, the local spins are more likely to form an anti-parallel spin ordering on two singly occupied dots. However, this magnetic-frustration phase is sensitive to the inter-dot coupling t, which breaks the symmetry of the three dots. As shown in Figs. 5(a) and 5(b), even t is just  ,
, 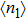 , and
, and 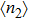 become different with
become different with  and
and 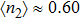 , accompanied with
, accompanied with  . Hence the electrons on dots 1 (3) and 2 are arranged anti-ferromagnetically. Besides, one notices
. Hence the electrons on dots 1 (3) and 2 are arranged anti-ferromagnetically. Besides, one notices 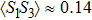 , thus the local spins on dots 1 and 3 are likely to be ferromagnetic due to the RKKY interaction mediated by t. Here,
, thus the local spins on dots 1 and 3 are likely to be ferromagnetic due to the RKKY interaction mediated by t. Here,  and
and 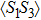 could not reach the ideal value of spin singlet and triplet respectively, for the ground state here is also frustrated, and the many-body states of
could not reach the ideal value of spin singlet and triplet respectively, for the ground state here is also frustrated, and the many-body states of 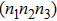 may include configurations such as (
may include configurations such as (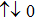 ) (or (
) (or (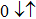 )), (
)), ( ) and (
) and ( ). As t increases to about
). As t increases to about  , one finds an abrupt change in
, one finds an abrupt change in 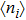 and
and 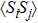 , indicating a first order QPT, e.g.,
, indicating a first order QPT, e.g.,  drops to 0.42, and
drops to 0.42, and 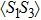 drops to −0.1. When t is large enough, e.g., t = 0.2,
drops to −0.1. When t is large enough, e.g., t = 0.2,  ,
,  ,
,  , and
, and  , thus dot 1 (3) is empty, while dots 3 (1) and 2 are singly occupied with antiparallel spin configuration, similar to the cases above.
, thus dot 1 (3) is empty, while dots 3 (1) and 2 are singly occupied with antiparallel spin configuration, similar to the cases above.
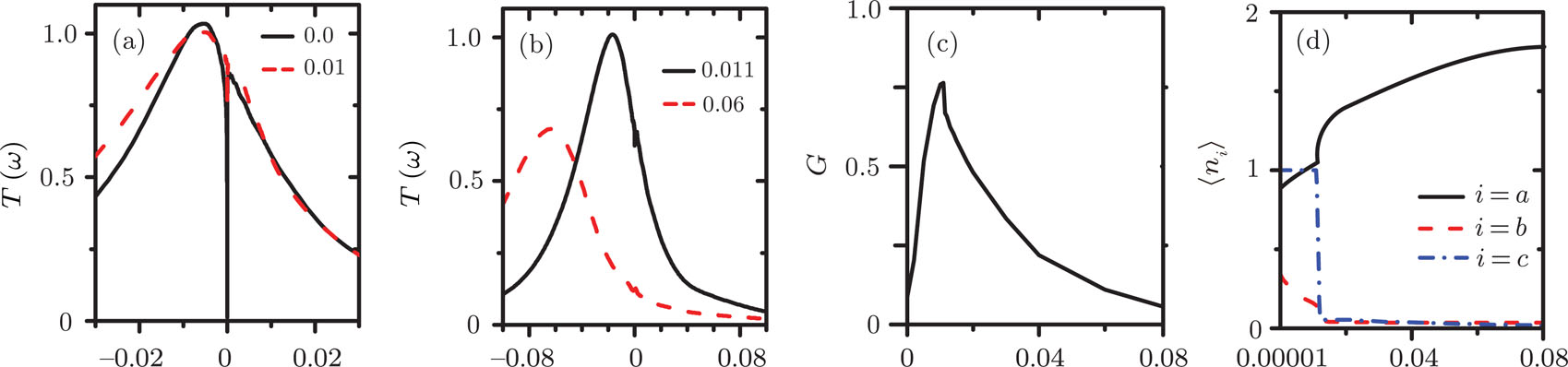
Figure 6(a) and 6(b) describe  for different t. It is seen when t is absent that there is a sharp dip at ω = 0, corresponding to zero conductance (see Fig. 6(c)), which could be attributed to the fact that in this case two singly occupied dots are arranged anti-parallelly, and the present PTQD model maps to a two impurity Anderson model with large inter-dot hopping and the Kondo peak is suppressed.[51] When t is turned on, e.g., t = 0.011, the dip is filled up continuously, and the charge transport is enhanced (Figs. 6(a) and 6(c)). In this process, the proportion of configuration (
for different t. It is seen when t is absent that there is a sharp dip at ω = 0, corresponding to zero conductance (see Fig. 6(c)), which could be attributed to the fact that in this case two singly occupied dots are arranged anti-parallelly, and the present PTQD model maps to a two impurity Anderson model with large inter-dot hopping and the Kondo peak is suppressed.[51] When t is turned on, e.g., t = 0.011, the dip is filled up continuously, and the charge transport is enhanced (Figs. 6(a) and 6(c)). In this process, the proportion of configuration (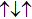 ) grows with increasing t, thus dot 1 (3) and dot 2 are more likely to form a spin singlet, and the remaining one contributes to the enhanced conductance. Correspondingly, the electrons on orbital
) grows with increasing t, thus dot 1 (3) and dot 2 are more likely to form a spin singlet, and the remaining one contributes to the enhanced conductance. Correspondingly, the electrons on orbital 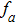 increase to about 1.0. However, in this regime, G could not reach the unitary limit since orbital
increase to about 1.0. However, in this regime, G could not reach the unitary limit since orbital 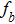 connected with
connected with  through a hopping term
through a hopping term 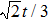 , which arises during the canonical transformation above, i.e., Eq. (7). Since orbital
, which arises during the canonical transformation above, i.e., Eq. (7). Since orbital  is isolated, the present model could be considered as a side-coupled double dot structure, and the conductance decreases with growing inter-dot hopping.[52] When t exceeds the critical point
is isolated, the present model could be considered as a side-coupled double dot structure, and the conductance decreases with growing inter-dot hopping.[52] When t exceeds the critical point 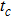 , a broadened peak develops at the left side of
, a broadened peak develops at the left side of  , which moves toward the left when t grows continuously. In this process,
, which moves toward the left when t grows continuously. In this process,  and
and 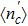 drop to zero, thus the PTQD model maps to a single impurity Anderson model. On the other hand,
drop to zero, thus the PTQD model maps to a single impurity Anderson model. On the other hand,  increases from 1.27 to 2.0 gradually, hence G decreases to 0.0 successively according to the Freidel sum rule.[53,54] It is worth noting that it is convenient for the critical point
increases from 1.27 to 2.0 gradually, hence G decreases to 0.0 successively according to the Freidel sum rule.[53,54] It is worth noting that it is convenient for the critical point  to be evaluated by the level of
to be evaluated by the level of  , i.e., with increasing t, the charge number
, i.e., with increasing t, the charge number  drops from 1.0 to 0.0, the critical point is just the point where the singly-occupied energy level of
drops from 1.0 to 0.0, the critical point is just the point where the singly-occupied energy level of  equals to the empty level, which gives
equals to the empty level, which gives  . In Fig. 5(c), we also show
. In Fig. 5(c), we also show  as functions of t for fixed ϵ = −0.008. One finds the behaviors are similar to ϵ = −0.01, thus our above discussions are robust in the regime
as functions of t for fixed ϵ = −0.008. One finds the behaviors are similar to ϵ = −0.01, thus our above discussions are robust in the regime 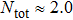 .
.
For initial charge number  , 5.0, and 6.0, the numerical results are similar to the cases
, 5.0, and 6.0, the numerical results are similar to the cases  , 1.0, and 0.0 respectively, due to particle-hole symmetry. Therefore, we neglect them in the present work.
, 1.0, and 0.0 respectively, due to particle-hole symmetry. Therefore, we neglect them in the present work.
4. ConclusionIn conclusion, we have studied the quantum phase transition and charge transport for a parallel triple dot device in the strongly correlated limit. We focus our attention on the effect of inter-dot hopping t beyond the Kondo regime, and we find the quantum behaviors depend closely on the initial electron number on the dots, which could be adjusted by the dot level through external gate voltage. For instance, when the initial charge number of the dots 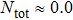 , it grows continuously with increasing t. When t is large enough, dot 1 (3) and dot 2 form a spin singlet, while dot 3 (1) is empty. The linear conductance G reveals a peak shape and reaches to almost its unitary limit at the point
, it grows continuously with increasing t. When t is large enough, dot 1 (3) and dot 2 form a spin singlet, while dot 3 (1) is empty. The linear conductance G reveals a peak shape and reaches to almost its unitary limit at the point  , where the bonding orbital is singly occupied and an orbital spin-1/2 Kondo effect could be found between the conduction leads and the bonding orbital. In the regime
, where the bonding orbital is singly occupied and an orbital spin-1/2 Kondo effect could be found between the conduction leads and the bonding orbital. In the regime 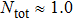 , G could be considered as a part of the above case and the quantum state is similar to the case
, G could be considered as a part of the above case and the quantum state is similar to the case  as t is large enough. When the initial charge number
as t is large enough. When the initial charge number 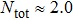 , we find the ground state is a magnetic-frustration phase and G is nearly zero when t is absent. This phase is sensitive to t, and is replaced by another mixture state even though t is just
, we find the ground state is a magnetic-frustration phase and G is nearly zero when t is absent. This phase is sensitive to t, and is replaced by another mixture state even though t is just 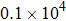 . G increases due to the charge number of the bonding orbital grows to 1.0. When t increases to
. G increases due to the charge number of the bonding orbital grows to 1.0. When t increases to  , a first order QPT could be found, and a large peak develops in the transmission coefficient
, a first order QPT could be found, and a large peak develops in the transmission coefficient  . As t is large enough, one of dots 1 and 3 forms a spin singlet with dot 2, while the remaining one is empty, similar to
. As t is large enough, one of dots 1 and 3 forms a spin singlet with dot 2, while the remaining one is empty, similar to  and 0.0 with large t.
and 0.0 with large t.
Our results could be used to describe the strongly correlated effects for triple level semiconductor or unimolecular electronic devices connected to the conduction band. We firmly believe that our work not only settled the underlying physical mechanism for the charge transport and phase transition for a PTQD system affected by the inter-dot hopping beyond the Kondo regime, but it may also provide appropriate guidelines for related experiments.