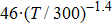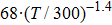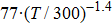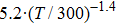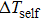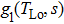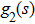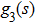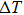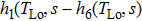† Corresponding author. E-mail:
Project supported by the Advance Research Foundation of China (Grant No. 9140Axxx501), the National Defense Advance Research Project, China (Grant No. 3151xxxx301), the Frontier Innovation Program, China (Grant No. 48xx4), and the 111 Project, China (Grant No. B12026).
In this paper, an efficient thermal analysis method is presented for large scale compound semiconductor integrated circuits based on a heterojunction bipolar transistor with considering the change of thermal conductivity with temperature. The influence caused by the thermal conductivity can be equivalent to the increment of the local temperature surrounding the individual device. The junction temperature for each device can be efficiently calculated by the combination of the semi-analytic temperature distribution function and the iteration of local temperature with high accuracy, providing a temperature distribution for a full chip. Applying this method to the InP frequency divider chip and the GaAs analog to digital converter chip, the computational results well agree with the results from the simulator COMSOL and the infrared thermal imager respectively. The proposed method can also be applied to thermal analysis in various kinds of semiconductor integrated circuits.
InGaP/GaAs or InGaAs/InP heterojunction bipolar transistors (HBTs) are widely used in mixed-signal, high-speed, or high-power circuits[1–4] with the advantages of high cut-off frequency[5–8] while maintaining high breakdown voltage.[9–11] Today, with the development of integrated circuits (ICs) and the growth in military and commercial applications, the size of HBT has been scaled down rapidly for higher operating frequency, leading to a huge number of devices integrated in a small chip and a higher current density. Because of the self-heating and thermal coupling effect, the thermal problem becomes more and more serious in HBTs.[12–14] With the temperature increasing in a device, the electrical device characteristics could degrade due to the thermal instability,[15–17] which reduces the reliability of the circuit seriously.[18–20] Therefore, it is of great importance to evaluate the distribution of temperature accurately during the design of integrated circuits.
With the technology of ICs entering into the nanometer domain, the thermal analysis for large ICs faces great challenges. Many improved numerical methods for fast thermal analysis were developed,[21–24] in which compact heat transfer equations are solved to characterize the temperature distribution in all parts of the IC chip including the thick substrate based on partitioning an IC chip into many discrete three-dimensional (3D) elements.[25,26] The accuracy of the temperature distribution increases with the number of discrete 3D thermal elements increasing. In this case, the calculation would be significantly time-consuming, which makes it hardly possible to achieve a large scale circuit.
However, the heat source generated by the active layer of each device in an IC is usually located in a thin layer close to the top surface of the IC chip, so only the temperature distribution within the related layer is of interest. For an HBT, the current flows from the emitter junction into the collector junction and the collector junction is at high reverse bias, so the power dissipation is mainly from the collector junction.[27] As a result, the collector junction will be the high-temperature region and the highest temperature will be located in the middle area between the base and collector, which is the so-called junction temperature. It will be easy to obtain the important temperature information of the IC chip with minor calculations if the highest temperature in this area is calculated for each heat source, avoiding a huge quantity of calculations of the numerical methods mentioned above.
In this paper, a semi-analytic temperature superposition method (SATSM) is proposed, based on the principle of superposition of temperature with considering the self-heating effect of the device and the thermal coupling effect between devices. The temperature distribution for the full chip can be easily depicted by calculating the highest temperatures for all devices in a chip with high efficiency and reasonable accuracy. Meanwhile, the temperature dependence of thermal conductivity on the thermal coupling from devices between each other should be considered in implementing the temperature superposition, otherwise, the measured temperature is higher than the calculated temperature and the difference increases with temperature increasing, especially in the high-temperature region.
A more accurate thermal analysis method based on an iterative algorithm, called SATSM-I, is proposed with considering the temperature dependent thermal conductivity. The SATSM-I shows higher accuracy while SATSM exhibits high efficiency and simplicity in calculation. The detailed steps of SATSM and SATSM-I are described in Section
Based on the principle of superposition of temperature, there are three factors to affect the thermal distribution, which include the self-heating effect of the individual device, denoted as 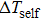

Therefore, the SATSM calculation procedure mainly consists of two steps.
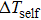
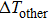
In this case, it is very convenient to obtain the temperature distribution of the HBT IC as long as the semi-analytic temperature distribution function for each device is determined. Each kind of device is firstly simulated by using COMSOL, and the semi-analytic function of the temperature distribution is obtained by fitting with MATLAB. Then, the highest temperature of each device will be worked out with the algorithm based on Steps 1.1 and 1.2, which is implemented in MATLAB.
Table 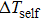
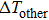
| Table 1.
Thermal conductivity of semiconductor material. . |
The influence caused by the thermal coupling effect from the adjacent device in a circuit can be equivalent to the change of local temperature TLo. Thus, TLo can be replaced by a slightly higher local temperature 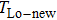
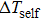
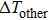
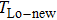

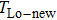
In order to realize the total computational process to obtain the temperature distribution of the HBT IC, the temperature distribution of each kind of device is first simulated by using COMSOL, and the semi-analytic function of temperature distribution is obtained by fitting with MATLAB, the same as the process made in SATAM. In the following, the GaAs HBTs with four sizes are taken for example to describe the total computational process.
Before making the function fitting for a single GaAs HBT, the model of each kind of device is first set and its temperature distribution is simulated by COMSOL. Figure 
 | Fig. 1. (color online) Schematic diagram of GaAs HBT simulation model, showing (a) top view and (b) sectional view. |
The collector–emitter current flows through the collector-base depletion region with high reverse voltage, resulting in the highest Joule heating. Therefore, heat generation comes from the collector-base depletion region.[30] In order to simplify the model, the power of each device is applied to the interface between the base and collector, which is called the heat source that is assumed to cover the emitter area as shown in Fig.
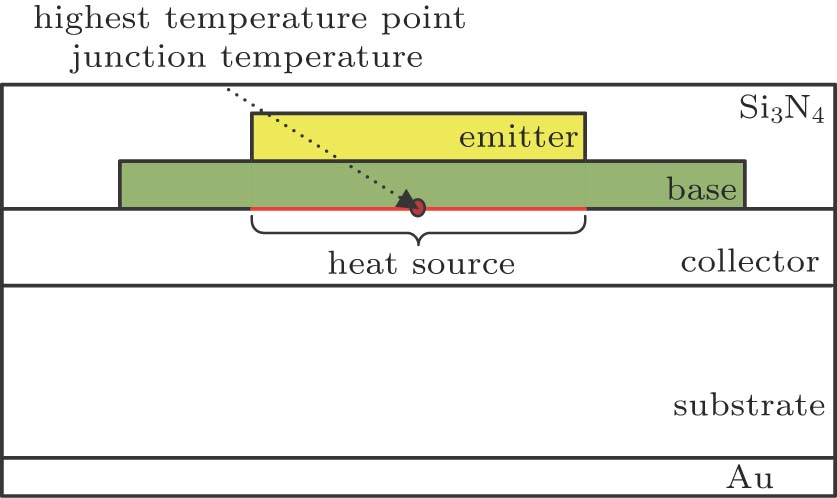 | Fig. 2. (color online) Position of the heat source and the highest temperature point in the simulation model. |
The 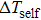
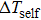

Figure 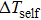
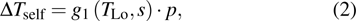
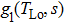
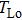

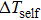
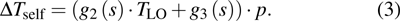
Since 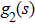
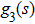
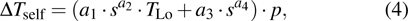
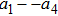
Then the junction temperature T(i) can be given as follows:

Based on the relationship between the junction temperature T(i) and the local temperature 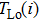
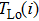
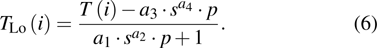

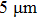
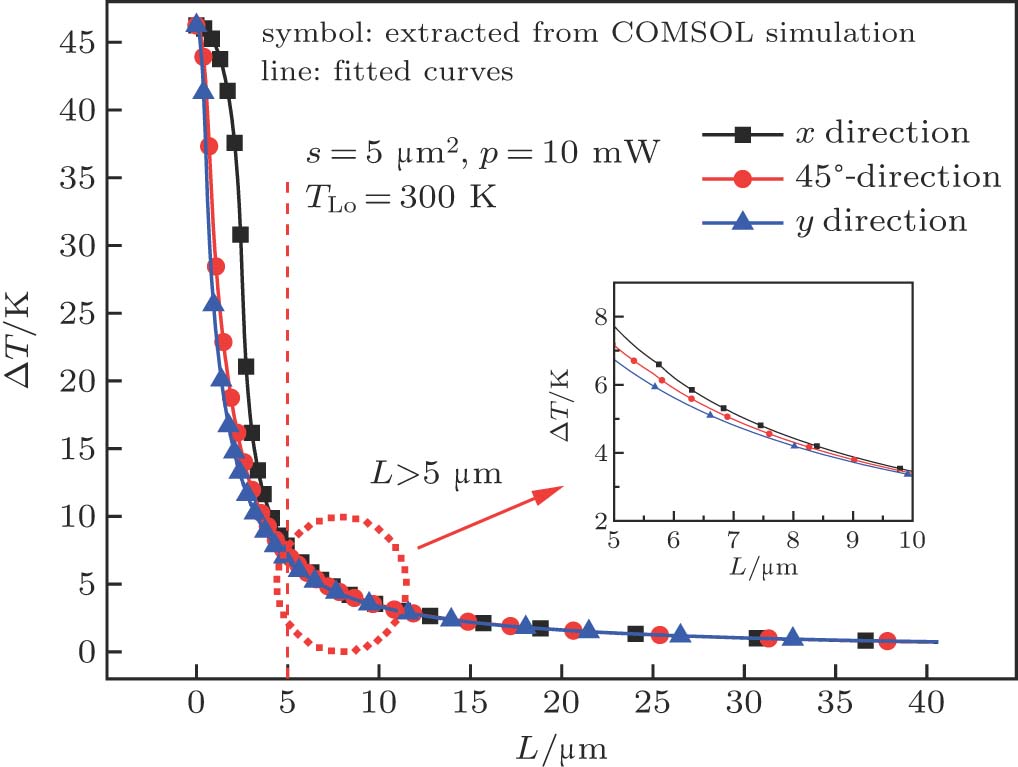
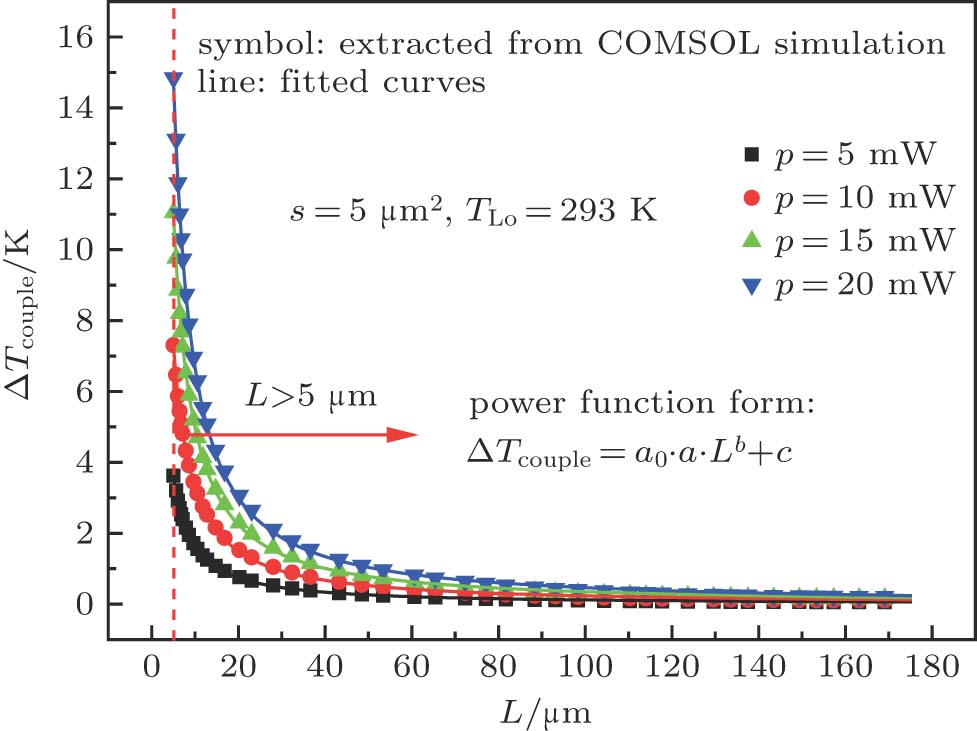
Whereas, for the distance larger than 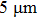
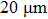
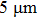
The temperature increment away from the center point is denoted as 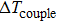
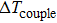
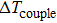
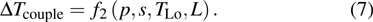
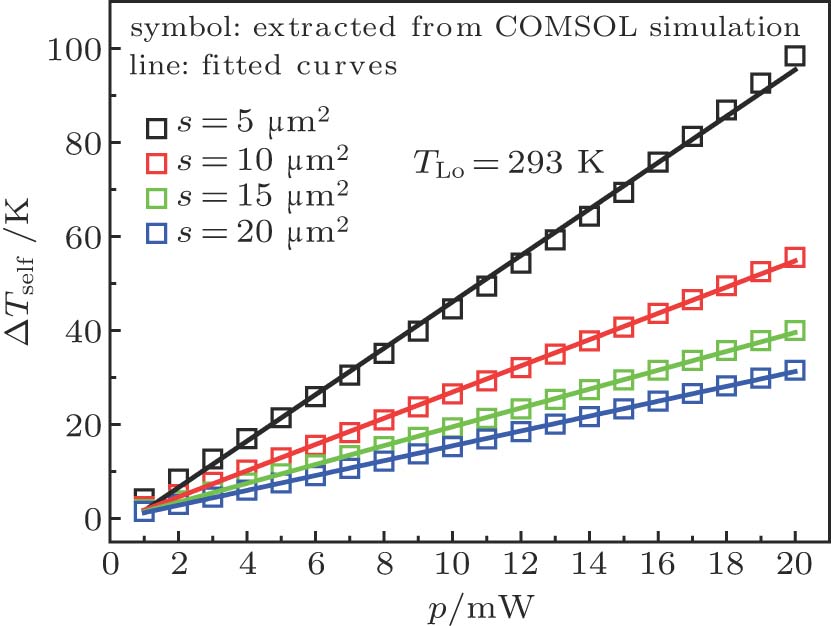
Figure 
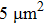
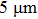
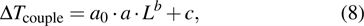

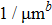
This power function of 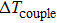
 | Fig. 8. (color online)  |
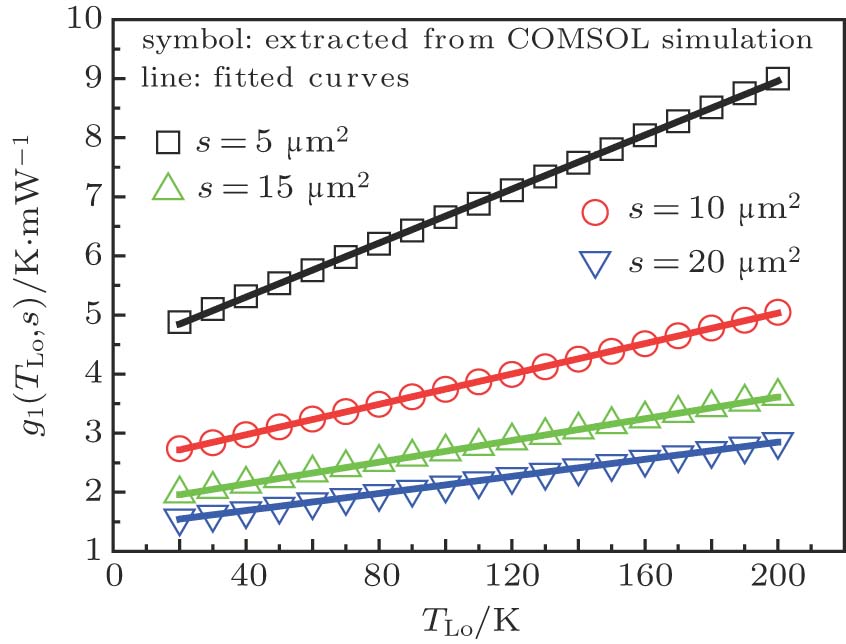
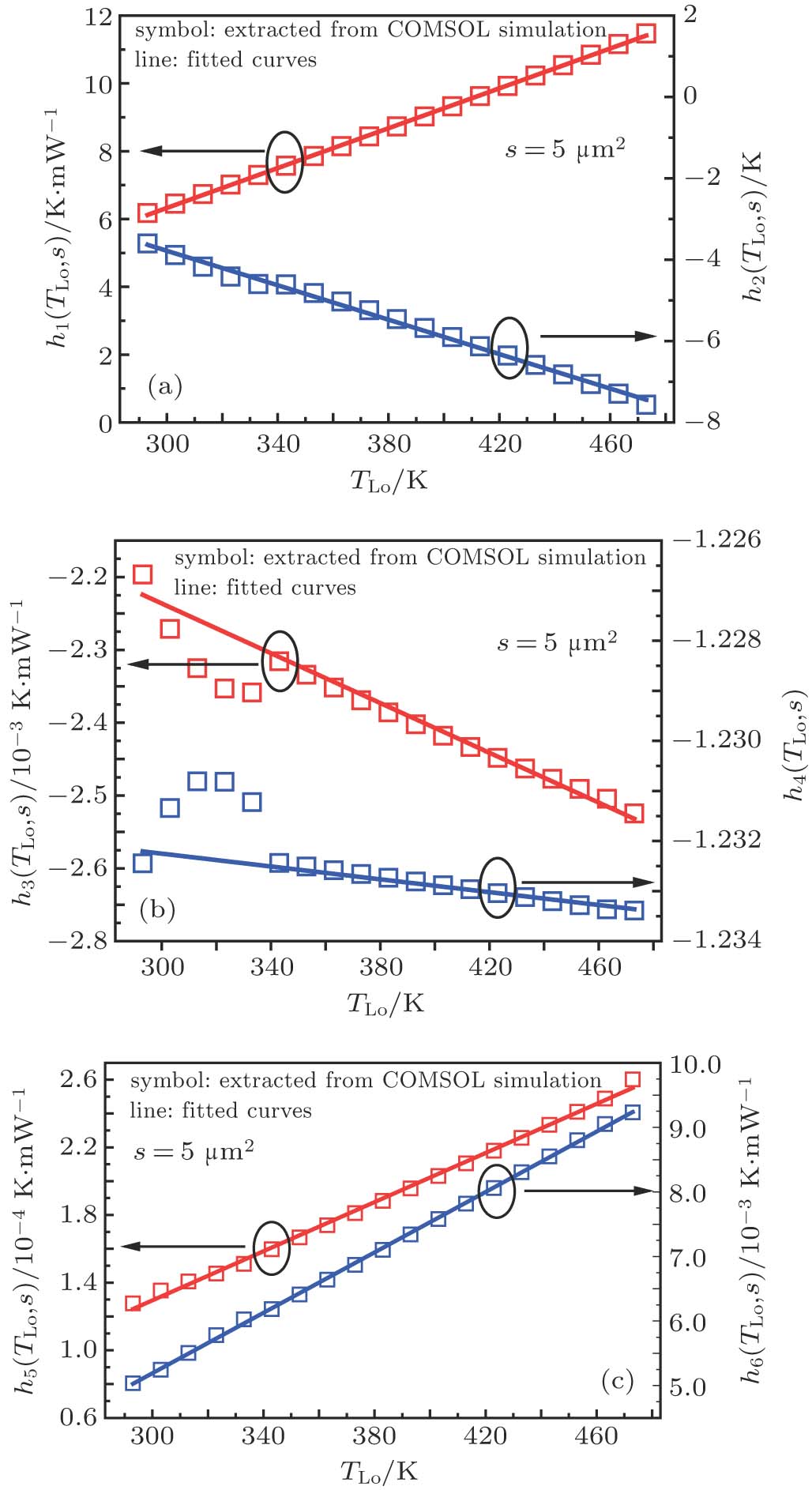
Figure 
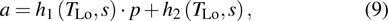


As shown in Fig. 
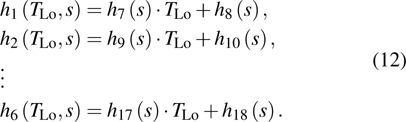
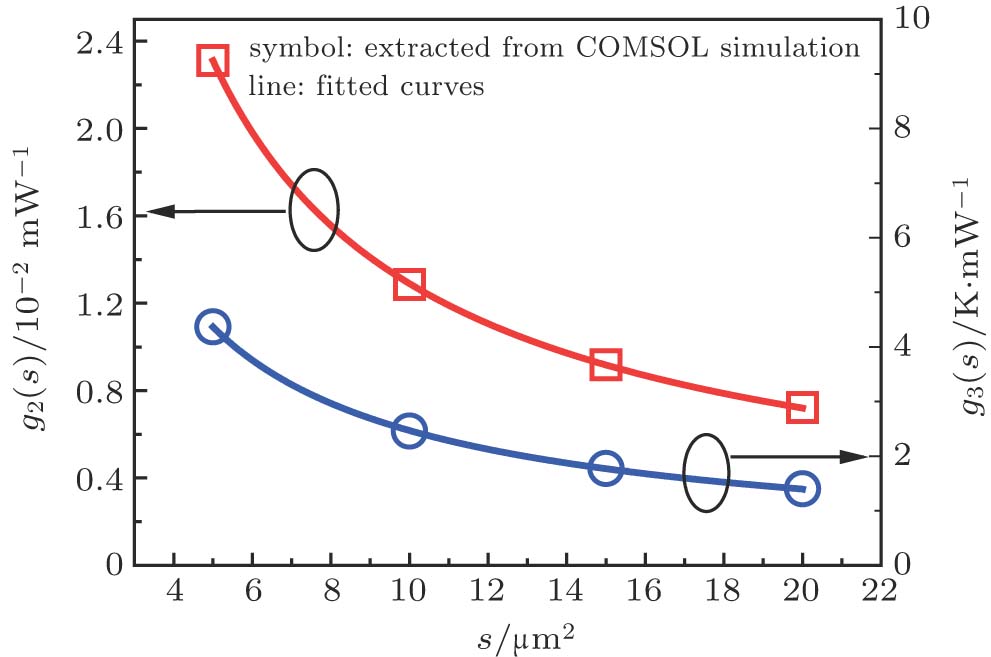
Then, the functions of 
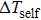

For an IC chip with n heat sources, the temperature increment at the center of heat source i is obtained by summing the temperature increment caused by source i itself and coupling heat from the sources of 

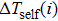

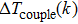

Based on Eq. (
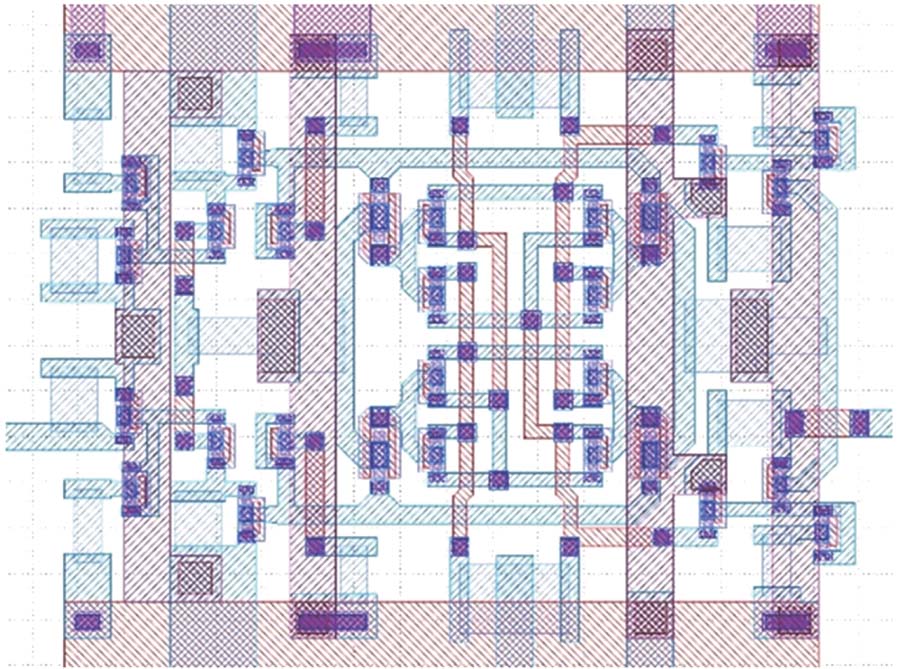
In this section, the method will be applied to the actual circuits. The SATSM and SATSM-I are codified by MATLAB on a Lenovo QiTianM6500-N000 desktop computer with 8-GB memory and an Intel(R) CoreTM i5-4570 CPU @3.20 GHz. The COMSOL is operated on a DELL R730 server with 128-GB memory and 2 Xeon (R) E–2683 V3 CPUs @2.00 GHz. The first example is an InP HBT frequency divider, which is a small scale IC. The layout of the circuit is shown in Fig.
The initial ambient temperature and local temperature surrounding the individual device are set to be 300 K. The calculations of the center temperature for each of all the devices are accomplished within 0.54 second and 0.69 second by SATSM and SATSM-I respectively, and the thermal profiles of the devices in the frequency divider are mapped using MATLAB for 28 devices and shown in Fig.
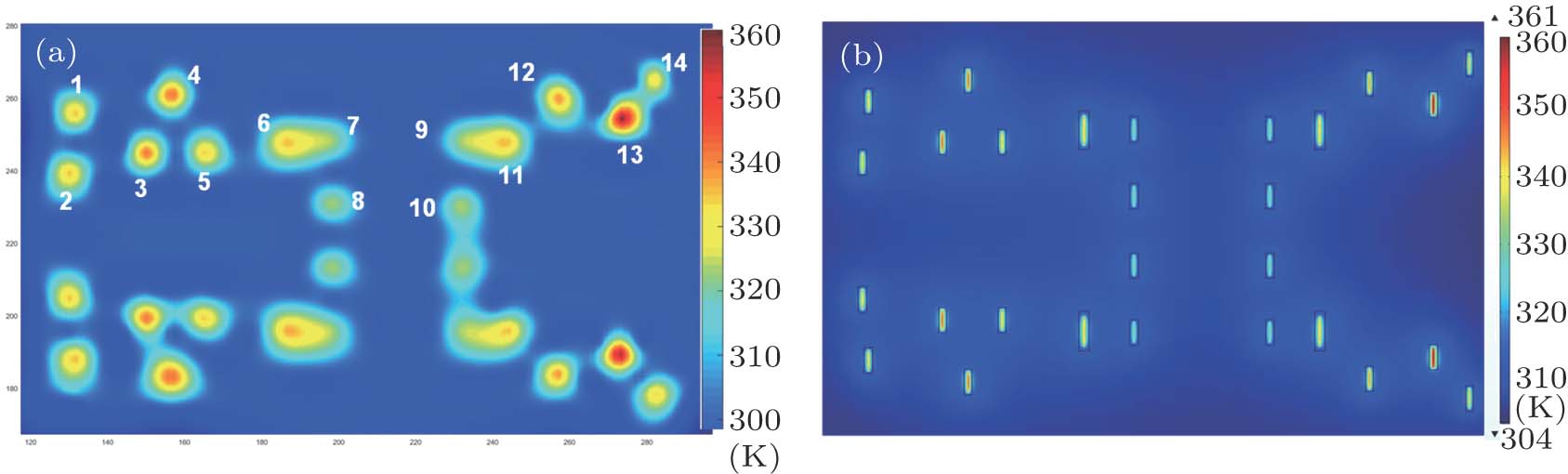 | Fig. 12. (color online) Thermal profiles of frequency divider, obtained from (a) SATSM-I and (b) COMSOL. |
In order to validate the temperature distribution, the simulation of the temperature distribution is performed by using COMSOL with a great number of grids, costing CPU time of about 3 hours with the peak memory usage of 100 GB as shown in Fig.
Table
| Table 2.
Comparison among temperatures of frequency divider, obtained from SATSM, SATSM-I, and COMSOL. . |
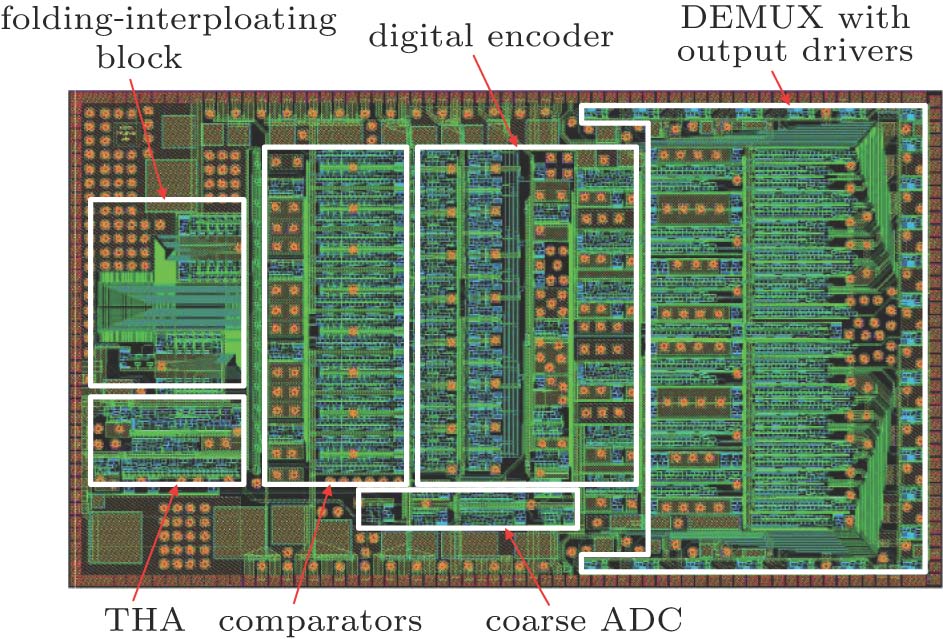
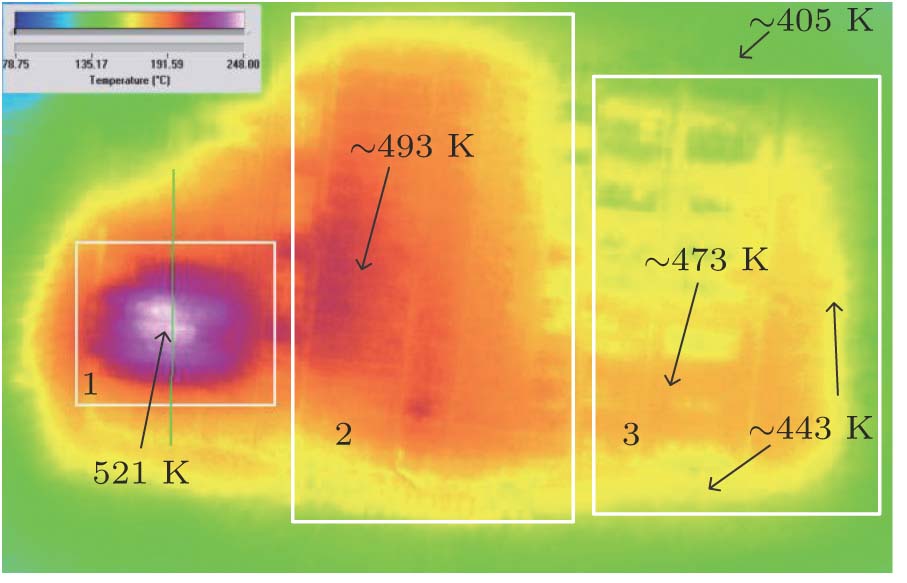
In order to verify the proposed method for large scale IC, a 6-bit 3-Gsps ADC chip is used as a testing example, including 3449 GaAs HBTs processed with 
For more than 3 thousand devices, a huge quantity of calculations would take unbearable computation time and memory if the simulation is implemented by using the simulator COMSOL, leading to it being far beyond the capability of the computer. However, this problem can be easily solved by the proposed method with only 58.61 seconds and 242.70 seconds by SATSM and SATSM-I respectively.
Figure
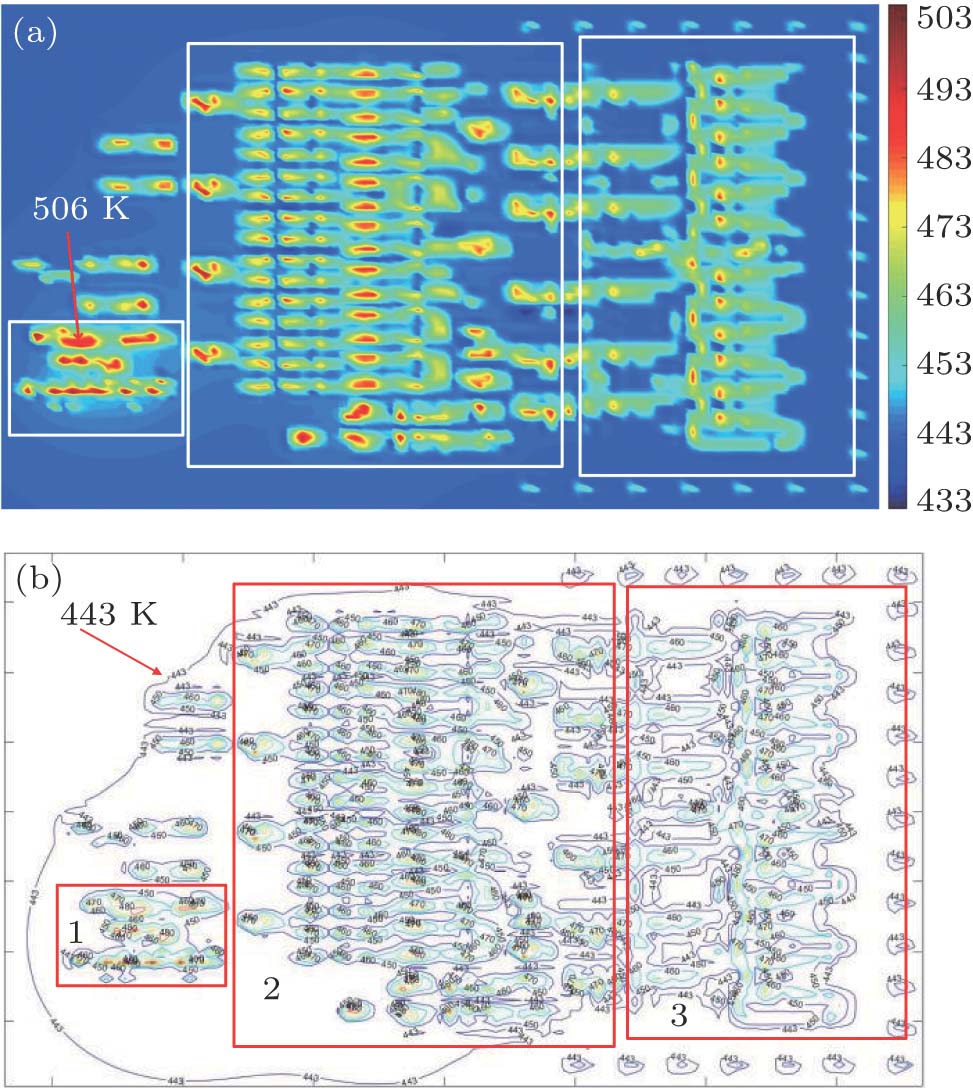 | Fig. 14. (color online) (a) Temperature distribution and (b) isothermal distribution of ADC from SATSM-I. |
From Fig.
Table
| Table 3.
Comparisons between chip temperatures calculated by SATSM-I and SATSM with measured values . |
As shown from Table
In summary, an efficient thermal analysis method SATSM-I has been presented for large scale compound semiconductor ICs based on HBT. Considering the temperature dependence of thermal conductivity on the thermal coupling effect and self-heat effect, the accuracy of the calculated result from the SATSM-I is significantly improved compared with the SATSM dealing with a fixed thermal conductivity, especially for the higher temperature region. However, the SATSM is also a good choice if power dissipation is lower because of its high efficiency and simplicity of calculation. Moreover, a relative error of the highest temperature from SATSM-I is only about 2.88%, achieving high efficiency operation. It is demonstrated that the proposed SATSM-I can be used in the calculation of temperature distribution and the thermal analysis design for a large scale compound semiconductor IC. Also, this method would be easily applied to other kinds of large scale integrated circuits.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |