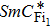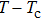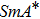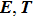
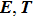
† Corresponding author. E-mail:
Fluorinated smectic liquid crystals each with a biphenyl benzoate rigid core are investigated. Molecular structures of the studied compounds have difference only in fluorine position and the length of the carbon chain. Dielectric relaxation study and electro-optical measurements are carried out with the classical SSFLC geometry. The field-induced phase transitions are studied and the (E,T) phase diagram is established.
Liquid crystals play an already important and still growing role in a variety of displays, modulators and a host of other electro–optical devices. Ferroelectric liquid crystals are promising materials for fast switching electro-optical displays with wide viewing angle.[1] Incorporating chiral smectic liquid crystals into display devices is extremely attractive.[2,3] But their widespread commercial use has not yet been realized. An active research revolves around the synthesis of new chiral smectic compound that possesses specific physical properties. In practice, very few elements can be used to modify the structure and properties of mesogenic phases, and thus retaining the mesogenity. Among substituents, the fluorine is very important one. Furthermore, the small size and high polarity of a fluoro-substituent can have some remarkable effects on the physical properties of liquid crystals. Phase behaviors,[4,5] physical,[6,7,11] dielectric,[12,13] and electro–optical[4,9,11–15] properties of fluorinated derivatives are dependent on the lateral fluoro-substituent location.[6–10] Such a variety leads to the interesting and advantageous tailoring of properties, both for establishing structure–property relationships, and for creating new applications.[2,3,11]
In smectic liquid crystals the molecules are arranged in layers with the director tilted with respect to the layer normal by a temperature-dependent tilt angle. Many phases are encountered with the same tilt inside the layers but a distribution of the azimuthal direction which is periodic with a unit cell of one (

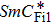




By the application of a sufficiently high electric field, in all these phases usually occurs a transition to the unwound 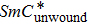
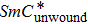
Isozaki et al. reported a field-induced phase transitions from a 3-layer intermediate phase to the 
In this paper, we first focus on the influence of the chemical structure on the diversity of the phases present for certain liquid crystals. Second, we report the main results concerning the influence of the fluorine position on the electro-optical properties and the (E,T) phase diagrams of two chiral smectic compounds.
In this section we present the results of thermodynamic studies of the phases transitions in chiral smectic liquid crystals. The classical thermodynamic approach makes it possible to explain the (E,T) phase diagram while the Landau–Degenne development makes it possible to envisage the evolution of the dielectric permittivity according to the temperature and thus to explain the experimental results of dielectric spectroscopy.
For the study of ferroelectric liquid crystals one must consider in addition to the common thermodynamic parameters the pressure p, the volume V, the temperature T, and the entropy S, two other electric parameters: the electric field E and the electric excitation D. Consequently, the variance of the system, “ferroelectric liquid crystal confined in an SSFLC cell”, becomes

For a pure substance the variance when two phases coexist is 2. The experiments on the liquid crystals are generally carried out at constant pressure, so that during a transition under electric field at constant temperature the value of the electric field is thermodynamically imposed.[22] If the transition is of the first order, the equilibrium between two phases results in a constant value of the electric field. We will therefore have δ E = 0 along the transition.
In the mean-field theory of the para-ferroeletric transition, if we consider the polarization P as an order parameter the Landau free energy is given as follows:[23]

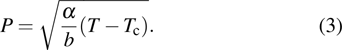
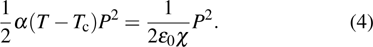
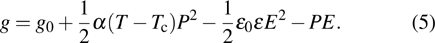


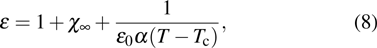

The phase transition can be lolated either by measuring the polarization P which vanishes at Tc or by looking for the dielectric constant ϵ and its divergence at Tc.
Now, if we consider the tilt angle as the principle order parameter, Landau’s free energy is then written as
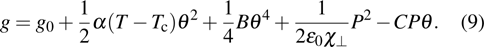



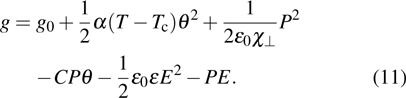

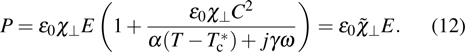


The liquid crystals studied are chiral smectic compounds belonging to two series of fluorinated products CnF3 and CnF2 (n = 7, 8, 10, and 12).[25,26] The molecular structure of these compounds and the zero-field phase sequence defined by dielectric spectroscopy are shown in Fig.
The smectic chiral compounds mentioned above were investigated by means of polarizing microscopy between crossed polarizers, where we used a polyimide coated planer glass cell with indium tin oxide (ITO) electrodes of 5-
We carried out experiments on the two products C12F3 and C8F2. The found results are compared with those of the products C10F3 and C7F2 in order to highlight the effects of the fluorine position and length of the carbonaceous chains on the properties of these products.
In the dielectric and electro-optic measurements, 5-
Dielectric spectroscopy studies were performed with a 7280 DSC lock-in amplifier that allowed measurements in the frequency window 10 Hz–2 MHz. During measurements, this system enabled us to superimpose direct bias voltages. The dielectric dispersion data were analyzed by fitting the temperature-dependent complex dielectric constant to the Cole–Cole equation:



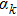
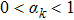
Figure
 | Figure 2. (color online) Three-dimensional plot of the imaginary part  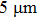 |
The peak at 110.8 °C is due to the soft mode (field-induced fluctuations in θ, also called electro–clinic effect) and indicates the low temperature border of 



We have already reported the phase sequence of C12F3 compound and we detect the coexistence of the two polar phases, 

Molecular structures of the compounds C12F3 and C10F3 differ only by the length of the carbon chain. The clarification temperatures decrease with the alkyl chain length increasing. In addition, they are lower for these compounds than C8F2 and C7F2.
The alkyl chain length also affects the mesomorphic behavior. Indeed, when the molecular length decreases, the domain of existence of the 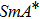

We note that the re-positioning of the fluorine atom from the 2- to the 3-position of the first benzene ring with respect to the chiral chain induces a transition mesophases temperature to decrease. Further, the fluorine position affects heavily the presence of certain phases. The temperature range of existence for the 


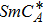
Concerning the appearance of polar phases, things are more ambiguous. The polar phases are missing in the compounds C10F3 and C7F2. The compound C8F2 present only the ferrielectric 

To explicate the structure property, the relationship geometries of the molecules are optimized by using the PM3 molecular mechanics method in a Chem–Draw–Ultra package.[28] The optimized structures of the molecules are shown in Fig.
The dipole moment is 3.3 D for the liquid crystals C10F3 and C12F3. Those of the compounds C8F2 and C7F2 have closed values 4.63 D and 4.62 D, respectively. Then it is the position of the fluorine atom, located on the benzene near the chiral center that affects the dipole moment but not the chain length. The value of the dipole moment increases for the compound with fluorine in the 2-position in benzene. The molecules structures are optimized with 0.09-kcal/Å molgradient. The dipole moment for C8F2 holds the value 4.63 D with the components −3.76, −1.4, and 2.3 D; then for C12F3 is equal to 3.3 D with components −2.1, −1.13, and 2.39 D. It is observed that the dipole moment increases systematically as fluorine atom moves from 3 to 2-position in benzene near chiral center as expected.
On the other hand, by comparing the molecular structures of CnF3 and CnF2 compounds, one notice a decrease in the distance between the fluorine atom and the chiral centre from 6.9 Å to 4.48 Å. The dipole moment is observed to increase. This rise in the dipolar moment is caused by the increased coupling between the dipole at the chiral center and the lateral molecular dipole. This is because of the electro-accepting fluorine substitution and the induction of the electric charge close to the dipole moment of the carbonyl group located close to the chiral center. This clearly illustrates that the electronic effects of a lateral fluoro-substituent are strongly dependent on the location.
To study the spontaneous polarization 
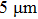
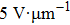
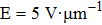
Figure 



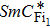
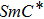

The field-induced phenomena, such as the transitions under electric field, are of very great importance for display applications. We present and explain the experimental results of the field induced transitions through measuring the spontaneous polarization and threshold fields. Figure
 | Figure 7. (color online) Plots of the polarization versus bias voltages for (a)     |
The polarization plot corresponding to the 
For the 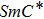

However, fora temperature range of 67.2 °C–79.4 °C where we assume the coexistence of two polar phases (
When 

We emphasize that in the 




At 64.2 °C, the sample presents the 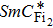
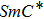
The constant current method allows the rapid localization of the transition threshold fields.[18,22] Figure
 | Figure 8. (color online) Evolution of cell voltage with time under a constant current of 5 nA for C12F3. |
The presence of two plateaus reveals the passage through an intermediate polar state between the phases null field, i.e., 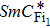


The field-temperature phase diagrams for both chiral smectic compounds studied are established. The method of plotting the (E,T) phase diagram through measuring the spontaneous polarization as a function of the electric field and the current constant method are used.
In the vicinity of the 


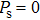



There are two different fields induced transitions in the 3-layer ferrielectric 

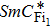
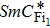





In the C8F2 compound, the anticlinic 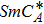

In conclusion, these diagrams show that no matter what the considered phase is, the transition to the unwound 


Fluoro-substitution in liquid crystals is employed for many different reasons, but the overall aim is to modify material properties in order to optimize electro–optic properties in applications.[34,35]
In this paper, we have presented an experimental approach to studying the influences of the chemical structure and the fluorine position on the phase behavior of certain fluorinated chiral liquid crystals. We report the main results concerning the electro-optical properties and the (E,T) phase diagrams of two chiral smectic compounds “C8F2 and C12F3”. A comparison with the results obtained before on two other products of the same family, i.e., C7F2 and C10F3, is carried out.[18,20,25]
The comparison of the phase sequence and behavior under electric field of the compound “C8F2” with those of others fluorinated smectic liquid crystals highlights the effects of the chain length and the position of the fluorine atom on temperatures phase transition and the mesomorphic stability.
The results of optimized geometry study by using the molecular mechanics indicate that the physical properties of these compounds are strongly dependent on the location of the lateral fluoro-substituent.
Both the position of the fluorine atom and the length of the carbon chain affect the phase sequence of fluorinated chiral smectic liquid crystal. It appears that the position of the fluorine has an influence on the nature of the phases present. On the other hand, the length of the chains has an effect on the phase transition temperature.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |