† Corresponding author. E-mail:
The subwavelength confinement feature of localized surface plasmon resonance (LSPR) allows plasmonic nanostructures to be functionalized as powerful platforms for detecting various molecular analytes as well as weak processes with nanoscale spatial resolution. One of the main goals of this field of research is to lower the absolute limit-of-detection (LOD) of LSPR-based sensors. This involves the improvement of (i) the figure-of-merit associated with structural parameters such as the size, shape and interparticle arrangement and, (ii) the spectral resolution. The latter involves advanced target identification and noise reduction techniques. By highlighting the strategies for improving the LOD, this review introduces the fundamental principles and recent progress of LSPR sensing based on different schemes including 1) refractometric sensing realized by observing target-induced refractive index changes, 2) plasmon rulers based on target-induced relative displacement of coupled plasmonic structures, 3) other relevant LSPR-based sensing schemes including chiral plasmonics, nanoparticle growth, and optomechanics. The ultimate LOD and the future trends of these LSPR-based sensing are also discussed.
Metallic nanostructures can confine external optical field to a deep-subwavelength volume by virtue of localized surface plasmon resonance (LSPR), resulting in near-field enhancement of orders of magnitude with respect to the incident light. The field enhancement has been realized as the major contributor to the enhanced Raman signal of molecules in close vicinity to metallic nanostructures,[1] as early as in 1970s.[2,3] This phenomenon is known as surface-enhanced Raman scattering (SERS) and has been further developed over the years as a sensing scheme for fingerprint molecule detection with a sensitivity achieving single-molecule level.[4–6] Another important consequence of the localized plasmonic field is that the LSPR frequency is extremely sensitive to refractive index (RI) variations around the metallic nanostructures. This remarkable feature has been exploited for the development of refractometric sensing, which is capable of single-molecule detection[7–9] since the sensing volume is comparable to the size of a single analyte. The analyte-induced RI change within the local field can be conveniently converted to a discernable variation of a far-field physical parameter, such as wavelength, intensity, phase, or even the color observed by naked eye, without the need for the introduction of complicated near-field optics or electrical contacts. As a superior approach to other molecular sensing schemes with the analytes limited to either light-absorbable[10,11] or fluorescence (labeled)[12] species, LSPR-based sensors can realize real-time label-free probing of non-absorbing molecules, free from bleaching or blinking (which always occurs in fluorophores-labelled techniques) and disturbance of the analyte kinetics (which always occurs in SERS or molecule-labeled assay). Compared to commercial surface plasmon resonance (SPR) sensing using surface plasmon polaritons (SPP) on a metal film, LSPR sensing is at least one order of magnitude less sensitive to bulk changes in the RI, while exhibiting an improvement in the vertical spatial resolution by an order of magnitude.[13] As a result, this technique shows a similar sensitivity in the case of molecular sensing, where the analyte is attached to the metal surface.[14] Remarkably, LSPR sensors have a much higher lateral spatial resolution than SPR sensors (the former can reach single-nanoparticle level). These advantages suggest that LSPR sensors are well-suited to next-generation modern sensor architectures, because they can be compactly integrated into a microfluidic chip with simple optical configuration requirements, and can be independently operated.[13] They can function over a wide spectral range with great flexibility since the LSPR frequency depends on the size, shape, material type and arrangement of the nanostructure.
As a spectroscopic technique, the limit-of-detection (LOD) of LSPR sensing is defined as the smallest detectable signal output (spectral change) induced by analytes or detected events,[15] and is mainly determined by two characteristic performances: i) the spectral resolution limit and ii) the spectral change capability induced by the analytes or events. In the case of the refractometric sensing scheme, the latter can be characterized by a dimensionless figure-of-merits (FOM), defined as the ratio of the peak shift per unit RI change to the full width at half maximum (FWHM) of the LSPR peak.[16] Obtaining a higher FOM depends on several key factors. These include the controlled delivery of analytes to local ‘hot spots’ around the metal nanostructures and the use of dark plasmons[17–28] with less radiative damping, such as the Fano resonances and cavity plasmons, which have smaller FWHMs. The improvements in the designs for plasmonic sensing over the last two decades would not be feasible without significant advances in nanofabrication technologies. On one hand, complex electron- and ion-beam lithography techniques enable complicated patterning that can be matched in a straightforward manner to the requirements of multiplexed on-chip devices. On the other hand, wet chemical synthesis can facilitate the fabrication of inexpensive, naked eye colored metallic colloidal with different geometries. They can also be used to develop complex structures by applying self-assemble and chemical-linking techniques, thus allowing for the precise control of extremely small features extended to large area scaling.
Plasmonic nanostructures placed in close mutual proximity show pronounced collective LSPR, which is sensitive to the displacement of the gap distance. The discovery of metal dimer structures (Refs. [5] and [6]) with extremely strong electromagnetic field enhancement in the nanogap region between two nanoparticles offers the physical bases for such super sensitivity and many other interesting phenonmena in various strong coupled plasmonic structures. By utilizing this plasmon coupling phenomenon based on spectral recognition of changes in the interparticle distance, a displacement sensing scheme known as the plasmon ruler has been developed to monitor dynamic physical, chemical or biological processes. Importantly, the aforementioned advantages/features of the LSPR-active nanostructures are primarily inherited to this plasmon ruler assay. Currently, sensing concepts based on plasmonic response changes have been extended to a broad range of interdisciplinary field, e.g., chiral sensing involving plasmonic fields[29] or self-assembly induced circular dichroism (CD) enhancements,[30,31] morphologic sensing schemes associated with nanoparticle growth[32] and active-plasmonic materials,[33] and plasmon nanomechanical transduction via the combination of a plasmon ruler scheme with a mechanical oscillator.[34] These tremendous developments broaden the boundaries of this research area to different degrees. Within this context, we will present an overview of the fundamental mechanism and current status of LSPR-based sensing associated with different transduction schemes, with an emphasis on the relevant strategies for improving sensing performance to achieve a sensitivity near the theoretical limit. In section
In a simple Drude’s scenario, the metal is treated as a free electron gas on a uniform background of positive charge. The performance of free electrons in the metal in response to an external electromagnetic field can be described by a frequency-dependent dielectric function ε(ω) according to the Drude model:[35]


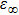
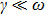

For a metallic structure with feature sizes down to nanoscale, its free electrons can be excited by an external electromagnetic field, thereby forming collective oscillations with the energy mostly confined to the surface. This phenomenon is known as LSPR, such that the localized polarization magnitude is described as 

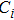


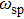



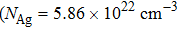
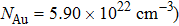
In terms of Eq. (
According to Eq. (

In practical applications, the LOD of the refractometric sensing is defined as the concentration of analyte derived from the smallest peak shift that can be recognized above the noise level, namely, the spectral contrast of the peak shift. This means that the LOD not only relates to the S, but also the FWHM of the LSPR peak. Generally, a larger nanoparticle exhibits a stronger and red-shifted LSPR peak, which leads to a higher S at the cost of an increased FWHM which lowers the spectral contrast. By taking these factors into account, a unit-less FOM was proposed to compare the overall sensing capability between different LSPR sensors, which is defined as the sensitivity S divided by linewidth FWHM.[16]

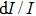

To date, the FOM of plasmonic structures serves as an important index for designing an LSPR sensor with higher sensitivity. The progress of FOM starts with ensemble nanoparticle synthesized by wet chemical approaches.[16,41–54] The LSPR peaks are non-homogeneously broad because of the non-uniformity of the sample, leading to a low FOM of 1–2. One way of addressing such a limit with regard to nonhomogeneity is to synthesize a mono-dispersed sample. For example, Burgin et al. used uniform Au bipyramids and obtained an FOM of 4.5.[53] Another way to get rid of nonhomogeneity is to perform single particle experiments.[42,44,59] As shown in Fig.
 | Fig. 1. (color online) FOM of individual nanospheres and nanocubes on a substrate. (a1) and (a2) LSPR peaks of a single Ag nanoparticle in different solvent environments, showing the linear relationship between the solvent RI and the LSPR wavelength, for which the FOM is 4.1.[42] (b1) and (b2) Scattering spectra of a Ag nanocube-on-glass in different dielectric environments. The narrower peak 1, quadrupole mode, sustains a sensing FOM of 5.4.[16] Reprinted with permission from Copyright 2003, 2005 American Chemical Society. |
Further improvement of the FOM was realized by developing the nanostructure supporting dark plasmons. Dark plasmons cannot be directly excited by plane waves and so they are free from radiative damping. Therefore, dark plasmons can facilitate a narrower peak with FWHM significantly smaller than that of the bright modes. An efficacious way to utilize dark plasmons is to create Fano resonances,[17–20,22–24,26] featured as a dip in the scattering spectrum originating from the interference between bright (superradiative) and dark (subradiative) plasmons. An early experimental demonstration by Sherry et al. in 2005, showed that a high FOM of up to 5.4 can be achieved using a single nanocube-on-glass system[16] (Fig.
 | Fig. 2. (color online) Refractometric sensing using dark plasmons. (a1) and (a2) Experimental demonstration of Fano resonances in an Au nanodisk heptamer can sustain a sensing FOM of 5.7.[20] (b1) and (b2) Cavity plasmons in an Ag nanocube dimer exhibit an FOM of up to 61, approaching the ultimate limit of the sensitivity.[28] Reprinted with permission from Copyright 2010 American Chemical Society, Copyright 2016 Royal Society of Chemistry. The unit a.u. is short for arbitrary units. |
A higher FOM can be obtained in a single nanorod geometry.[25,26] A high aspect ratio nanorod can be viewed as a Fabry–Pérot type cavity, where the SPP travels along the long axis and is reflected by two terminals. The resulting standing wave patterns on the nanorod defines the multipolar plasmon resonances based on the number of nodes. It was shown that higher order modes provide a higher FOM due to their narrower linewidth. Simulation predictions show that the FOM of the third order cavity mode is as high as 29. In 2016, Zhang et al. introduced a highly tunable dark plasmon for refractometric sensing with a sensitivity approaching the upper limit of any LSPR sensor.[28] (Fig.



 | Fig. 3. (color online) Progress of FOM towards approaching the theoretical limit. (a) The FOM of LSPR-based sensors versus year, which is not a complete list but highlights the trend of FOM improvement. The blue (red) circles show the measured (calculated) results, where the numbers inside the circles represent the citation number of the appropriate references. (b) FOM of the cavity plasmons compared with the theoretically predicted FOM obtained by J & C permittivity,[28] which suggests that the cavity plasmons are approaching the ultimate sensitivity limit of the LSPR-based sensing. Reprinted with permission from Copyright 1994, 2001, 2002, 2005, 2006, 2009, 2010, 2011 American Chemical Society, Copyright 2016 Royal Society of Chemistry. |
The aforementioned discussions mainly focused on the refractometric sensitivity contributed solely by the LSPRs. One of the most remarkable features of the LSPR sensor is that each individual plasmonic structure can work as an independent sensor. The lateral spatial resolution can be up to the single nanoparticle level, which inherently breaks the diffraction limit of light.[13] In fact, the FOM of plasmonic sensors can be substantially enhanced by at least one order of magnitude[63] by using lattice plasmons in periodically arranged plasmonic structures. Lattice plasmons originate from the diffractive coupling among the plasmonic elements. As a result, the FWHM of lattice plasmons is usually less than 10 nm, which significantly exceeds the theoretical limit of the pure LSPR peak.[64–66] As shown in Fig. 
 | Fig. 4. (color online) Refractometric sensors using lattice plasmons. (a1) and (a2) Subradiative collective modes excited in a suspended nanohole array show extremely narrow peak with FOM reaching 164.[55] (b1) and (b2) Lattice plasmons obtained in gold mushroom arrays, with FOM of ∼108.[56] Reprinted with permission from Copyright 2011 National Academy of Science, Copyright 2013 Nature Publishing Group. |
It should be noted that the significant improvement of the FOM of the lattice plasmons is at the cost of losing the nanoscale lateral spatial resolution when compared to individual LSPR-based sensors. This is because the lattice plasmons are delocalized collective modes associated with multiparticle long-range coupling or grating effects, excited by periodic plasmonic structures with large areas. On the other hand, the sensitivity to bulk RI changes of an SPR sensor is generally an order of magnitude higher than that of a lattice plasmon-based sensor.[13] However, by comparing the vertical field decay length between lattice plasmons and SPP, it can be determined that the higher FOM of propagating plasmons is at the expense of a lower vertical spatial resolution by approximately one order of magnitude.[71] A comparison of the LSPR mode, lattice mode, and SPP mode is shown in Fig.
In addition to FOM, spectral resolution is another key factor in determining the LOD in all of the spectrometric or ratiometric sensing schemes. In this case, the resolution is defined as three times the standard deviation of the noise that corresponds to a confidence level of about 90%.[72] Compared to the SPR sensor, the LSPR sensor benefits from a much smaller sensing volume and therefore suffers significantly less fluctuations due to the environment temperature or vibration.[71] Apart from these factors, the output noise that limits signal identification is mainly attributed to three types of noise sources:[73] (i) the intensity fluctuation of the light source, (ii) the shot noise that originates from the Poisson statistical photon flux, which can be effectively reduced by collecting more light under the saturation levels, and (iii) the inherent noise of the photodetector. In the case of spectroscopic sensing, all three noise sources can be effectively reduced by averaging time-series signals collected from the same detector (called time averaging). In this situation, the spectral resolution is proportional to the factor 
To process the output signal, numerous algorithms have been developed.[75] Although most of them are created to readout the signal from a SPR sensor, they can also be straightforwardly applied to determine the spectral shift of the LSPR peaks in a similar manner. Beyond the simplest recognition method that directly reads the strongest point of a peak fitted by a Lorentz or Gaussian function, the most commonly used algorithms include the centroid method,[71,76–79] polynomial fitting,[71,76,80,81] optimal linear data analysis,[82] projection method,[83] integrated response technique,[84] etc. In the centroid method, the determination of the LSPR peak position is based on the calculation of the center-of-mass from the part of the peak above a certain baseline. The center-of-mass will be obviously affected by the noise of light intensity if a fixed threshold is set to an asymmetry peak. Thus modified strategies, such as dynamic,[77,78] weighted,[76] and fast[79] centroid methods have been developed to reduce the influence of light intensity fluctuations. Another well-known approach with a resolution comparable to the centroid algorithms is to fit the LSPR peak (above a certain threshold) using polynomial functions, where the peak position is determined by the extremum of the polynomial functions. Apart from calculating the shift of the peak maximum, some new strategies that utilize the asymmetrical shape changes of the LSPR far-field spectrum have been introduced to improve the spectral resolution based on the second order derivative spectrum, e.g., monitoring the variation of the curvature[85] and inflection points.[86]
By applying the centroid and polynomial fitting algorithms using a fast 2 s integration time, Dahlin et al. demonstrated how to obtain a peak position with a precision higher than 



LSPR-based sensors mainly benefit from their nanoscale sensing volume due to the near-exponential decay property of the local field away from the structure surface. In terms of this feature, the LSPR-active nanostructures serve as a natural label-free molecular sensor for real-time detection of biomolecules and related kinetics processes without perturbing the analyte.[58,88] For molecular sensing, analyte binding events only result in local RI changes near the plasmonic surface. Therefore, compared with the FOM that represents the RI change of the total environment, a more comprehensive index called the FOMm has been considered in the form of:[89]

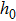
As shown in Eq. (
 | Fig. 6. (color online) Strategies for improving the molecular sensitivity (a) Increasing the analyte size by binding extra molecules.[93] (b) Small gas molecules detected using high-resolution spectroscopy.[95] (c) Single-molecule detection by photothermal microscopy.[9] Reprinted with permission from Copyright 2005, 2010 American Chemical Society, Copyright 2012 Nature Publishing Group. |
Another effective sensing scheme for detecting small dye molecules is based on the coupling between plasmons and molecular resonances.[96–98] The spectral shift caused by the dye molecule binding event is significantly amplified when the molecular absorbance overlaps with the LSPR of the nanostructures to some degree. Zhao et al. exploited the fact that small camphor molecules can generate amplified LSPR shifts by tuning the LSPR near the resonance of a CYP101 protein,[97] in which case the average shift per camphor molecule was ∼0.07 nm. Apart from camphor molecules, Rhodamine 6G[98] and MgPz[96] molecules also exhibit similar effects that cause a pronounced spectral shift, demonstrating the possibilities for sensitive detection of a wide range of small dye molecules.
Improving molecular sensitivity is one of the major efforts in the application of LSPR sensors. This requires a discernible spectral response to facilitate reporting on analytes with a smaller size (thickness), lower weight or lower molecule number. In recent years, the LOD of individual LSPR sensors have improved from, e.g., 


The aggregation of nanoparticles in noble metal colloids leads to color changes of the solution, resulting from the appearance of dramatic red-shifted broad peaks that dominate the far-field spectrum.[102] Early in 1997, this plasmonic coupling-based feature had been utilized to selectively probe oligonucleotides with the LOD down to 10 fM.[103] The further progress of chemical and biological applications involving the self-assembly and aggregation of nanoparticles has been comprehensively discussed in the review article of Saha et al.[104] The plasmonic response of the coupled nanostructures can also be quantitatively modified by tuning the gap distance between the structures. This gap-distance dependent plasmonic response can be developed as ‘plasmon rulers’ to monitor nanoscale interparticle distances or distance changes, by observing the optical spectrum of the coupled nanoparticles.[105] In order to apply the plasmon ruler for displacement sensing applications, it is necessary to calibrate the LSPR peak position as a function of the interparticle separation. Su et al. reported a phenomenological law related to this gap-distance dependent interparticle coupling effects.[57] They measured the scattering spectra of lithographically fabricated elliptical disk pairs with various sizes and gap distances and demonstrated that the LSPR peak shifts follow a near-exponential function in relation to the interparticle distance (Fig.




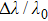
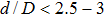
 | Fig. 7. (color online) Universal near-exponential decay behavior of different plasmon rulers. (a)–(c) Radiating antenna plasmons in elliptical nanodisk dimer[57] (a), nanodisk dimer[107] (b), and NPOM[115] (c). (d) Cavity plasmons in nanocube dimer system.[28] Reprinted with permission from Copyright 2003, 2007, 2012 American Chemical Society, Copyright 2016 Royal Society of Chemistry. |
In essence, the near-exponential decay performance of the plasmon ruler can be well understood in a physically intuitive manner called the plasmon hybridization model.[116–118] This model is rigorously analogous to the molecular orbital theory: the molecular orbital results from the hybridization of individual atomic wave functions. In the simplest case of two adjacent nanoparticles[117] separated by a distance d larger than the diameter of the nanoparticles, the nanoparticle dimer can be approximated as bonded classical dipoles (with angular momentum l = 1) through Coulomb interaction. The hybridization of the dipoles results in red-shifted low-frequency bonding (blue-shifted high-frequency antibonding) dipole plasmon mode, such that the shifts are symmetric and follow a 



According to the nonlinear trend of the plasmon ruler equation, the decrease of the gap distance results in an increasing redshift of the bonding plasmon mode. This implies that a higher displacement sensitivity can be obtained for a smaller gap distance. This sensitivity is dramatically improved when the plasmon ruler is applied to a gap distance smaller than 5 nm. However, the fabrication of such a narrow gap is a challenging task when considering current nanofabrication technologies with regard to spatial control of the interparticle separation, with sub-nanometer accuracy in three dimensions. Benefiting from the highly uniform size and shape in the fabrication of nanoparticle dimers with various geometry, the lithographic pattern method plays a primary role in systematically understanding and calibrating the performance of plasmon rulers over a wide spacing range. However, this method suffers from serious limitations in regards to fabricating the gaps and their interval is significantly narrower than ∼5 nm.[114] Moreover, these lithographic fabricated patterns are naturally fixed on the substrate, which hampers their use as displacement sensors. Colloidal synthesized nanoparticle dimers with narrow gaps linked by molecules can overcome the aforementioned limitations in principle. However, they are still limited because of the complexity of the analysis which must be performed, i.e., optical identification of the individual dimers and their steric configuration from other multi-nanoparticle complexes based on light polarization studies and electron microscopy.
A simple approach to minimizing the preceding complex issues for the development of a well-controlled narrow gap is to place a nanoparticle in close proximity to a metal mirror, thereby forming a nanoparticle-over-mirror (NPOM) system. The NPOM system can be modeled as a plasmon hybridization between the nanoparticle and its electromagnetic image induced within the metal mirror,[118] whose optical behavior closely resembles the dimer system in some aspects. In the NPOM setup, the gap distance can simply be tuned down to an atomic length scale by functionalizing an organic/dielectric spacer layer on the metal mirror (or the surface of the nanoparticle) with varying thickness. Furthermore, every nanoparticle situated on top of this spacer layer is naturally created as a plasmon ruler with uniform particle-film separation and a spatial orientation, which can be easily extended to large area applications and significantly simplify the experimental characterizations. In comparison with the dimer system, the bonding plasmon mode in the NPOM shows a larger peak shift in response to equal changes of the gap distance. This is because the contributions from higher-order angular momentum states of the NPOM plasmon are stronger than that of the dimer case.[102] Hill et al. experimentally investigated the plasmon ruler properties of the NPOM system and its displacement sensitivity in a very narrow gap region.[115] The NPOM is spaced by an organic layer with a thickness ranging from 2 nm to 0.5 nm, where the smallest interval can down to that of a single C–C molecular bond (∼0.18 nm). At the narrowest 0.5-nm separation, the displacement sensitivity can up to a 5 nm peak shift per Ångström thickness change (5 nm/Å, shown in Fig.
Recently, it has been theoretically predicted that for narrow gap distance, the cavity plasmons have the potential to be used in displacement sensing with a sensitivity significantly higher than that of the radiating antenna plasmons. As shown in Fig.
 | Fig. 8. (color online) NWOM plasmon rulers using cavity plasmons.[121] (a) Near-exponential decay performance of the cavity plasmons with sensitivity reaching  |
According to the classical Maxwell descriptions, both the plasmon hybridization model and the universal scaling performance of the plasmon ruler suggest that the displacement sensitivity increases monotonically as the gap distance decreases, thus encouraging the development of plasmon rulers with ever narrower gaps. However, recent progress both in theoretical[122] and experimental[123,124] studies suggest that the classical electromagnetic model fails to predict the plasmonic behavior over very narrow gap distances (especially at the sub-nanometer scale) due to the emergence of quantum mechanical effects, such as nonlocal screening and electron tunneling. In the quantum regime, the bonding plasmon modes show slower wavelength redshifts and finally vanish, along with the appearance of a charge transfer plasmon before the gap distance is reduced to zero.[125] This means that the quantum effects set the ultimate limits on the displacement sensitivity, where the maximum sensitivity is obtained at the narrowest gap before the electron tunneling becomes dominant. According to the quantum corrected model,[122] the electron tunneling probability not only depends on the width of the gap junction but also on the conductivity in the gap junction. Vacuum or air junctions have the lowest electrical conductivity, and the tunneling effect usually occurs below a 0.5 nm gap distance.[124] For the cube dimer structure using 1,4-benzenedithiolates (BDT) as a spacer layer with a larger conductivity,[126] the charge transfer plasmons appear at ∼1.3-nm gap distance. Lerch et al. studied the plasmon ruler behaviors of a DNA linked Au nanoparticle dimer system by varying the DNA length.[127] They found that the plasmon ruler followed the universal exponential decay function when the gap distance was larger than 2.8 nm. For a shorter gap width, the emergence of quantum mechanical effects strongly modifies the response of the bonding plasmon mode, whose shifted resonance wavelength depends on the gap morphology. This transformation gap distance reaches ∼2.8 nm due to the higher conductivity of the DNA spacer layer. Therefore, in order to obtain a higher displacement sensitivity, the conductivity of the gap region in the plasmon ruler should be as low as possible, so that the plasmon ruler can operate in a narrower gap distance before the emergence of quantum mechanical effects.
The aforementioned plasmon ruler systems mainly focus on the LSPR peak shift caused by the change in the gap distance in dimer-like systems. In this section, we will introduce more complicated systems, where the relative displacement or deformation of the plasmonic elements cannot solely be described by one-dimensional gap distance variations. In this case, the plasmon modes used to represent structural deformation mainly utilizes Fano resonances. The spectral properties of the Fano resonance for plasmon ruler systems can be approximately divided into three types: (i) a fixed Fano dip wavelength with varied linewidth, which can be viewed as the opposite shifts of two adjacent peaks, or radiance sensing monitoring of the depth of the dip, (ii) a fixed Fano dip with a varied broad superradiant peak, and (iii) the wavelength, width and depth of the Fano dip are all changed. The most complicated case includes both the peak shift and the radiance change. Hentschel et al. designed a plasmonic nanodisk heptamer, and showed that the Fano resonance originated from the coupling between the center nanodisk and the other surrounding elements.[128] By decreasing the relative separation among all of the nanodisk elements, they found that a continue redshifted Fano dip with an increase in depth starts to appear due to the strong inter-disk coupling. This coupled structure could be viewed as a plasmon ruler for sensing the in-plane stretching or breathing mode of the substrate beneath. Shao et al. developed an individual Au nanorod–nanosphere core-satellite system,[129] where the presence of small Au nanoparticles results in the symmetry breaking of the nanorod’s electromagnetic environment, thereby significantly modifying the spectral shape. The plasmonic responses associated with the Fano resonance are sensitive to the position and gap distance of the Au nanoparticle with respect to the nanorod, which can serve as a two-dimensional polar-coordinate-based plasmon ruler. Gallinet et al. reported on a dolmens-like nanostructure consisting of an individual cuboid suspended on top of a side-by-side separated nanorod dimer,[61] where the cuboid (nanorod dimer) supports the strong radiative dipolar (nonradiative quadrupolar) mode. In-plane movement of the top cuboid with respect to the center of the nanorod dimer leads to the appearance of an LSPR dip with varied FWHM and intensity, which originated from the plasmonic dipole-quadrupole coupling effect (Fig.
 | Fig. 9. (color online) Plasmon rulers associated with symmetry breaking. (a) Displacement sensors based on a radiative sensing scheme.[61] (b) Three-dimensional displacement sensing based on Fano resonance.[130] (c) Displacement sensing in vertical and horizontal directions measured via the spectral shift and splitting of the cavity plasmons.[28] Reprinted with permission from Copyright 2013 American Chemical Society, Copyright 2011 American Association for the Advancement of Science, Copyright 2016 Royal Society of Chemistry. |
By observing the radiance change at the dip wavelength instead of relying on the wavelength shift, they demonstrated that this coupling feature can be used for structural sensing with Ångström scale displacement sensitivity. As shown in Fig.
In 2005, Sönnichsen et al. first applied the concept of the plasmon ruler to chemical and biological sensing.[105] They developed single pairs of metal nanoparticles linked by flexible DNA tethers. Changes of the interparticle distance were triggered by the events of DNA hybridization, which were reported in real-time by measurement of the spectral shift of the LSPR peak (Fig.
 | Fig. 10. (color online) Some typical applications using plasmon rulers. (a) Monitoring of DNA hybridization events using nanoparticle dimer.[105] (b) Detecting MMP3 proteins secreted from live cells.[141] (c) Probing of drug response by selective detection of caspase-3 in live cells.[145] (d) Cavity plasmon-based humidity sensing resulting from the thickness change of a PVP layer filled inside the NWOM cavity.[121] Reprinted with permission from Copyright 2005 Nature Publishing Group, Copyright 2015 American Chemical Society, Copyright 2018 Nature Publishing Group. |
Due to the pronounced bright color spot that can be detected using a microscope with excellent photophysical stability even in a complex environment, plasmon rulers also serve as a powerful platform for elucidating the complex transient interactions and dynamic biological processes that occur in living cells. The intra-/extra-cellular position and interparticle distance of plasmon rulers can be determined by simple light-scattering microscopy. Lee et al. demonstrated the specific and reversible detection of single matrix metalloproteinase molecules secreted from mammary epithelial live-cells by DNA-linked nanoparticle pairs.[141] In their experiments, the binding of target molecules onto DNA aptamers resulted in changes of the interparticle distance (Fig.
In addition to biological assays, the concept of plasmon rulers has also been widely utilized for various physical and chemical applications including color switching,[146] gas sensing,[121,147] as strain force transducers,[148,149] pH sensing,[149] etc. For example, Powell et al. developed a thin fluoropolymer spaced nanocube-on-mirror system as a plasmonic humidity sensor.[147] An increase in humidity leads to the swelling of the fluoropolymer via strong water adsorption from its surroundings, which is reflected in a spectral redshift of the cavity plasmons. The authors demonstrated that this plasmon ruler system was capable of a maximum sensitivity of 0.57-nm peak shift per relative humidity change. However, this sensitivity was achieved by varying the polymer thickness from 11 nm to 24 nm, a gap distance range which had not previously exhibited the advantages of the cavity plasmon harbored in narrow gaps. To achieve a higher sensitivity of the cavity plasmon, Chen et al. designed a NWOM system for sensing water molecules, where the spacer analyte film used to adsorb these molecules was only 2-nm thickness.[121] They determined that the sensitivity could be increased up to 1.28-nm peak shift per relative humidity change (Fig.
The chirality of an object can be interpreted as a mirror image which does not coincide with the original object. A chiral material shows different complex dielectric functions under right- or left-handed illumination. On one hand, the difference of the imaginary part leads to the different absorptance of the right or left circularly polarized light, which is known as the circular dichroism (CD). On the other hand, the difference associated with the real part causes the phase change of these two circularly polarized components to be different. As a result, linearly polarized light will be rotated after passing through a chiral medium, where the linearly polarized light serves as the superposition of right- and left-handed light. This phenomenon is known as optical rotatory dispersion (ORD). Many biological molecules exhibit chirality, such as amino acids, carbohydrates, nucleic acids and proteins, and many of them only express one handedness. Therefore, the CD and ORD spectra are powerful methods for revealing the secondary structure of macromolecules as well as their deformation and dynamics.[150] However, the measurement of the CD and ORD of the high chirality biological molecules and materials require a high concentration or a large volume of analyte due to their very weak optical chiral response. Probing trace amounts of chiral molecules requires signal amplification, which can be effectively realized using LSPR,[151–153] e.g., by combining chiral plasmonic structures with chiral molecules. In such hybrid chiral systems, the CD response of the chiral molecules was modified, or the CD response occurred in the ultraviolet wavelength (the chiral molecules’ region) to the visible wavelength (the LSPR’s region). Maoz et al. demonstrated a CD response for two-layer chiral molecules covering the surface of a plasmonic structure,[154] whereas the natural chiral optical response of the molecules themselves was unmeasurable. As shown in Fig.
 | Fig. 11. (color online) LSPR-based chiral sensing. (a) Improvement of the CD response of the chiral molecule by plasmonic field enhancement.[155] (b) and (c) Probing of analyte biomolecules by analyte trigged self-assembly method using strongly coupled nanoparticles[30] (b) and nanorods[31] (c). Reprinted with permission from Copyright 2013 American Chemical Society, Copyright 2013 Nature Publishing Group. |
In general, even a dense chiral molecule solution can only provide ∼10 millidegree of CD response, while that of the plasmonic structure can exceed ∼10 degrees. This is because the absorption and scattering cross-section of the latter are much larger than those of the former.[151] Therefore, a smart scheme has been developed to realize ultrasensitive chiral sensing: the analyte chiral molecules trigger the self-assembly of the plasmonic elements in solution, forming strongly coupled plasmonic structures that exhibit a much stronger CD signal. For instance, Wu et al. developed a heterodimer consisting of a large Au and a small Ag nanoparticle bridged by analyte biomolecules, to form a scissor-like geometry with a slightly twisted dimer axis.[30] The linked biomolecule can then be detected by measuring the large CD response of the dimer system (Fig. 
Changes in the size and shape of plasmonic structures can also strongly modify their LSPR response, which in turn can be used as the basis for the development of plasmonic sensors to detect the physical, chemical and biological processes that induce the morphologic change of the plasmonic structures. A widely used method associated with nanoparticle enlargement for sensing biomolecules is bio-catalyzed reactions. In this scheme, the analyte behaves as a reducing agent to promote the growth of the nanoparticles situated in the solution, thereby resulting in a significant spectral change. Zayats et al. reported on the H2O2-mediated growth of Au nanoparticles that demonstrated the potential of this scheme for glucose sensing.[32] The H2O2 was produced from glucose by the catalysis of a glucose oxidase (GOx) and was used to reduce the Au ions into gold atoms in solution. This enzyme catalyzed assay has also been applied to the probing of a cancer biomarker prostate-specific antigen, with a LOD of 
The transformation between the metallic and dielectric properties of a nanomaterial can be viewed as an equivalent dimensional change of the LSPR-active structures. For example, metallic magnesium nanoparticles can be transformed into dielectric MgH2 particles, resulting in the disappearance of the plasmonic response. Furthermore, the MgH2 can be converted back into Mg in the presence of oxygen. The media involved in these switching processes are known as active plasmonic materials.[33] Duan et al. fabricated hybrid plasmonic nanostructures composed of Mg and Au nanoparticles with geometries that depict strong chiral optical response.[167] Upon hydrogen loading with increasing concentration, the CD response of the mixed structure gradually decreased due to the change of the plasmonic response via the conversion of Mg into MgH2, and the reverse process occurred during the loading of oxygen. This study shows the potential for the development of active plasmonic platforms for a variety of gas detection schemes. Furthermore, the active plasmonic features of Mg have been extended for display applications.[168,169] An Mg nanolayer over an Al mirror separated by hydrogen silsesquioxane pillars of different heights can act as individual display pixels, whereby the color depends on the concentration of hydrogen loading. Apart from the Mg and MgH2, similar processes can also work in the case of Ag and AgCl by electrochemical means, as demonstrated by Byers et al.[170] In their study, the Ag or AgCl served as the shell on the surface of the Au nanoparticle dimer, and the transition from the metallic Ag to dielectric AgCl leads to a spectral shift of a bonding plasmon and the emergence of a charge transfer plasmon due to the change in the effective gap distance. Therefore, Ag-based plasmonic structures also manifest the potential for probing various processes that can trigger the transition between metal and dielectric states.
With a built-in readout of the nanomechanical oscillator’s motion displacement by analyzing the transmitted and reflected light from the cavity, cavity optomechanics[171] has developed into an important field for precise sensing of displacement (motion),[172–175] force,[176–179] and mass,[180–183] etc. However, the exploitation of the optomechanical coupling strength, which is highly related to the overall sensitivity, is unable to achieve the minimization requirements of the nanomechanical resonators due to the diffraction limit of light. The confinement of a conventional optical mode in a cavity is approximately 
As shown in Fig. 
 | Fig. 12. (color online) LSPR-based cavity optomechanics. (a) Plasmon nanomechanical coupling of nanoscale separated beams.[184] (b) Plasmo-mechanical resonators based on dimer nano-antennas.[186] (c) Nanomechanical motion transduction with high order cavity plasmons.[34] Reprinted with permission from Copyright 2013, 2015 American Chemical Society, Copyright 2016 Nature Publishing Group. |
However, with the development of optomechanics, the combination of LSPR and optomechanical nano-oscillators is encumbered by two major problems. The first problem is that compared with traditional dielectric microcavities, plasmonic nanocavities have a significantly lower Q-factor due to the inherent properties of plasmonic materials. Plasmo-mechanical systems may be more widely used for precise measurement and sensing only if this disadvantage can be effectively addressed. The second problem is the imprecision which arises from the weak and continuous measurement of two quadratures simultaneously: namely the position and the momentum. The conventional weak measurement is limited by the quantum mechanical Heisenberg uncertainty principle, especially for measurements where the precision is close to the zero-point fluctuation. In order to make meaningful progress towards breaking through this limit, single-quadrature measurement should be performed in order to measure one quadrature to an arbitrary precision.[187,188] Backaction evading measurement,[175,188,189] which has been realized in conventional optomechanical systems should be performed and reproduced in plasmo-mechanical systems to circumvent the limitation imposed by the uncertainty principle.
In this review, we discussed some of the most important and promising research findings associated with LSPR-based sensing, especially the individual plasmonic structures with spatial resolutions down to the nanoscale. The operation of the most of these sensors can be generally summarized as the effect of analytes or their relevant events that trigger spectral changes of the LSPR in plasmonic structures. They are detected via minute variations of their surrounding RI (refractometric sensing), displacement (plasmon ruler and plasmo-mechanical) or geometry (chiral sensing, active plasmonics and bio-catalysis, etc.). The resulting sensor output is then effectively read using far-field optics and is associated with corresponding changes in wavelength, intensity, phase, etc. Based on these principles, the LOD of an LSPR sensor mainly depends on the FOM of the plasmonic structure, as well as the spectral resolution of the measurement system. On one hand, the FOM is strongly related to the level of light confinement and sensing volume of the plasmon mode. The progress of the FOM associated with the choice of plasmon modes, generally developed from radiating bonding of plasmons to Fano resonances, and finally to cavity plasmons that manifest the potential of achieving the ultimate limit of the LSPR sensing sensitivity. On the other hand, a higher spectral resolution with a faster collection time is actively being pursued to realize real-time single-molecule detection with smaller molecular mass. These requirements are also desirable for precise monitoring of displacement with the goal of sub-picometer level detection using static plasmon rulers as well as oscillatory optomechanical transducers. In the future, the development of LSPR-based nanosensors will likely be divided into two main categories: one is to achieve low-cost, high-throughput and on-chip biosensing using simpler sample fabrication procedures, with the goal of single-molecule sensitivity for even smaller masses and higher selectivity, achieved by cheap and portable instruments. Another direction is the creation of a plasmonic nanocavity that facilitates the monitoring of ultrasmall cavity separation changes over ever smaller length scales. This could in principle be used for in-situ probing of very weak physical or chemical processes in atomic-thickness scale materials, e.g., photoinduced stress, piezoelectric effects, optomechanics, atomic intercalation, and thermostriction, where the vertical dimensional changes need to be tracked with unprecedented accuracy and detail.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] | |
| [114] | |
| [115] | |
| [116] | |
| [117] | |
| [118] | |
| [119] | |
| [120] | |
| [121] | |
| [122] | |
| [123] | |
| [124] | |
| [125] | |
| [126] | |
| [127] | |
| [128] | |
| [129] | |
| [130] | |
| [131] | |
| [132] | |
| [133] | |
| [134] | |
| [135] | |
| [136] | |
| [137] | |
| [138] | |
| [139] | |
| [140] | |
| [141] | |
| [142] | |
| [143] | |
| [144] | |
| [145] | |
| [146] | |
| [147] | |
| [148] | |
| [149] | |
| [150] | |
| [151] | |
| [152] | |
| [153] | |
| [154] | |
| [155] | |
| [156] | |
| [157] | |
| [158] | |
| [159] | |
| [160] | |
| [161] | |
| [162] | |
| [163] | |
| [164] | |
| [165] | |
| [166] | |
| [167] | |
| [168] | |
| [169] | |
| [170] | |
| [171] | |
| [172] | |
| [173] | |
| [174] | |
| [175] | |
| [176] | |
| [177] | |
| [178] | |
| [179] | |
| [180] | |
| [181] | |
| [182] | |
| [183] | |
| [184] | |
| [185] | |
| [186] | |
| [187] | |
| [188] | |
| [189] |


