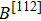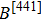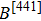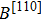† Corresponding author. E-mail:
Recently, the Dirac and Weyl semimetals have attracted extensive attention in condensed matter physics due to both the fundamental interest and the potential application of a new generation of electronic devices. Here we review the exotic electrical transport phenomena in Dirac and Weyl semimetals. Section
In 2016, for theoretical discoveries of topological phase transitions and topological phases of matter, Thouless, Haldane and Kosterlitz were awarded the Nobel Prize in physics. By introducing the topological concepts from mathematics, they opened the door on a new world in physics where new and exotic phases of matter emerge. On the basis of their remarkable work, great progress has been made in the theoretical understanding and experimental realization of topological states over the past decade. In particular, topological materials have attracted widespread attentions since the discovery of topological insulators (TIs)[1–8] and become an important frontier in condensed matter physics.
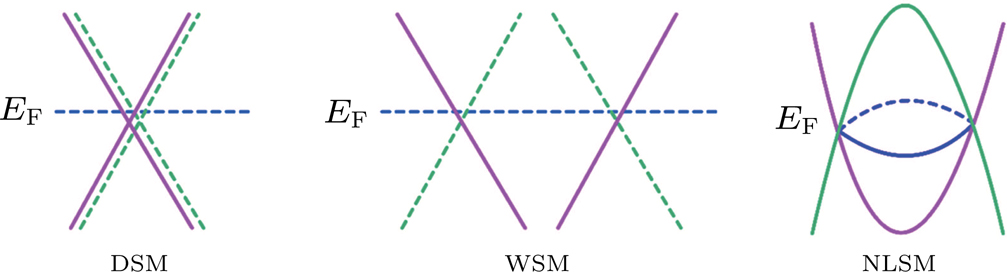
Recently, the focus has moved towards topological semimetals (TSMs) since the theoretical proposal of a three-dimensional (3D) Weyl semimetal (WSM) in a magnetic phase of pyrochlore iridates.[9–16] TSMs are characterized by the symmetry protected band crossing in the Brillouin zone (BZ) at or close to the Fermi level. Based on the degeneracy and momentum space distribution of the nodal points, the currently most studied TSMs can be classified into three classes (Fig.
In DSMs, the band crossings are isolated points with four-fold degeneracy, known as Dirac points (DPs) or nodes.[11,15,16] Graphene is an example of two-dimensional (2D) DSMs, in which the DPs are fragile. As the analogy of 3D graphene, 3D DSMs possess bulk DPs that are robust against perturbations.[14] The 3D DSMs are expected not only to show similar exciting phenomena and applications found in graphene but also to exhibit unusual properties such as giant diamagnetism and oscillating quantum spin Hall effect with the thickness.[15–17] In addition, the DSMs are at the boundary of various topological phases and can be regarded as the parent compounds to realize other topological states, such as WSMs and topological superconductors (TSCs).[17] The DSM state has been sought by studying the topological phase transition in Bi1−xSbx,[18] TlBi(S1−xSex)2,[19–21] Hg1−xCdxTe,[22] (Bi1−xInx)2Se3,[23–25] Pb1−xSnxSe,[26] (Bi1−xSbx)2Se3[24] etc., while the realization of a stable DSM phase in these systems is still challenging due to the requirement of fine-tuning composition. In 2014, the presence of stable DSMs was identified in Na3Bi and Cd3As2 by angle-resolved photoemission spectroscopy (ARPES) experiments[17,27–30] after the theoretical predictions from one group in China.[15,16] The experimental verifications ignite intensive studies in these two materials,[31–36] where Cd3As2 has become the most studied DSM system due to its chemical stability in atmosphere. Besides, the DSM states were also suggested in other materials, such as BiZnSiO4 family,[37] BaAgBi family,[38,39] TlMo3Te3 family,[39] PtBi2,[39] Cu3PdN,[40] and the elemental α-Sn.[41]
For a WSM, the band crossings are isolated points with two-fold degeneracy, known as the Weyl points (WPs) or nodes, and play the role as monopoles in the Brillouin zone.[9–11] In fact, the Dirac node is composed of two Weyl nodes with opposite chirality overlapping each other in the momentum space (Fig.
In a NLSM, two bands cross each other along a closed curve in the momentum space. The curve where the bands cross is called a nodal line, which may take the form of an extended line across the BZ, or a closed loop inside the BZ, or a chain consisting of several connected loops (nodal chain).[69] In 2011, the NLSM was theoretically proposed to exist in a fine-tuned superlattice of a normal insulator and a TI with broken time-reversal symmetry (TRS).[70] A series of realistic materials were then predicted to host the NLSM state, which include the Mackay-Terrones crystals,[71] PbTaSe2,[72,73] CaAgX (X=P, As),[74] Ca3P2,[75] TITaSe2,[76] Cu3PdN,[40] etc.[11,69] Recently, the experimental studies have presented some evidence for the NLSM phase in several bulk materials such as PbTaSe2,[73] ZrSiX (X=S, Se, Te),[77–79] and PtSn4.[80] Moreover, the 2D nodal line fermions were also discovered in monolayer Cu2Si based on combined theoretical calculations and ARPES measurements.[81]
In this chapter, exotic electrical transport phenomena in Dirac and Weyl semimetals under magnetic fields are mainly reviewed. In Section
In 2013, based on the first-principles calculations, Wang et al. proposed that Cd3As2 is a symmetry-protected DSM with a single pair of 3D Dirac points in the bulk and nontrivial Fermi arcs on the surfaces.[16] Subsequently, the direct experimental evidences for the confirmation of Cd3As2 as a DSM were obtained from the ARPES results,[27–30] which immediately stimulates intensive studies on the properties of Cd3As2. Several groups from China and the United States, almost at the same time, soon reported the electrical transport properties of Cd3As2 bulk crystals, in which striking features like the ultrahigh mobility and the large MR are revealed.[33–36]
In general, the single crystals of bulk Cd3As2 are synthesized from a Cd-rich melt in the evacuated quartz ampoule.[90] In the isolation from the finally resulting materials, two kinds of samples are mainly investigated. One is the needle-like single crystal with well-defined facets, in which the longest axis lies along [110] and the largest face is normal to [112]. The other is the large chunky multidomain crystals which lack defined facets. The crystal quality of Cd3As2 largely influences the transport properties, which might show a rich spectrum even when the samples are from the same batch.[33–35] For example, the mobility of Cd3As2 at 5 K can vary from 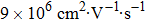
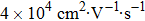
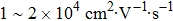
In Liang et al.’s report, the mobility of the DSM Cd3As2 can be as high as 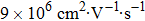
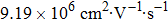
In a magnetic field, a very large MR 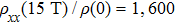


In the light of the Abrikosov’s theory,[91] a quantum linear MR can be expected to occur beyond the quantum limit (QL) in a gapless semiconductor with linear energy dispersion, where all the carriers occupy the lowest Landau level. Though the linear MR behaviors have been observed in Cd3As2 as mentioned above, their origins cannot be attributed to this scenario since the observed linear MR exists at very small magnetic fields.[33,34,36] Almost at the same time, Zhao et al. studied the MR of Cd3As2 at an ultrahigh magnetic field up to 60 T. With increasing magnetic field, the Cd3As2 single crystal exhibits obvious SdH oscillations and the Zeeman splitting appears (n= 2, 1.5) when the Fermi level is nearly pushed into the lowest Landau level. The sample reaches the QL at about 43 T. With further increasing magnetic field beyond the QL 
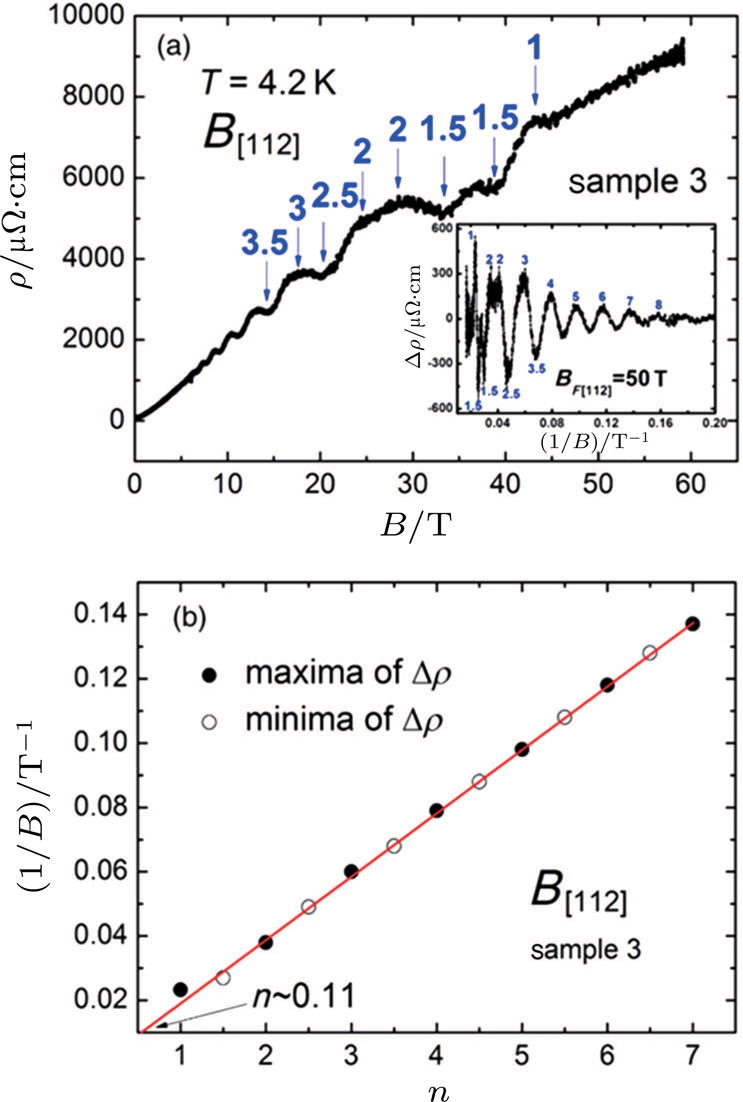 | Fig. 2. (color online) (a) Magnetoresistivity of Cd3As2 up to 60 T. Inset: SdH oscillations after subtracting a polynomial background. The linear MR beyond the quantum limit (n=1) is a reminiscence of the Abrikosov’s quantum MR model. (b) The Landau fan diagram of SdH oscillations.[35] |
In addition, nonsaturating linear MR persisting up to 65 T was also observed in the n-doped Cd3As2 system.[92] The MR variation was consistent with the results of the classical disordered model originating from fluctuating mobility, and thus it was suggested to be caused by the inhomogeneous mobility distribution.[92]
On the giant MR of DSM Cd3As2 crystals, there is usually a superimposition of the SdH oscillations, which are the manifestation of the intrinsic Landau level properties. Analyses on the SdH quantum oscillations can obtain important parameters of the material, such as the mobility, the carrier density, the Dingle temperature, the transport time, etc. Besides, it is believed that the nonzero Berry phase, a distinguished feature of Dirac fermions, can also be identified by plotting the Landau fan diagram of the SdH oscillations. The oscillations can be described by the Lifshitz-Kosevich formula 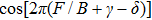
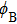
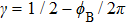
For the Cd3As2 single crystals, He et al. observed a phase shift 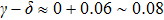
In a magnetic field, the SdH oscillations can be a very useful tool to detect the information of the Fermi surface. However, the magnetotransport measurements of the SdH oscillations in one direction or by rotating the magnetic field in a certain plane can only get a glimpse of a small part of the complete 3D Fermi surface of Cd3As2. An overall study on the transport properties of Cd3As2 at different magnetic field directions would be of interest for a comprehensive understanding of the DSM Cd3As2. Zhao et al. mapped an overview of the Fermi surface of Cd3As2 single crystals for the first time by systematic electrical magnetotransport measurements,[35] complementary to previous ARPES experiments.[27–30] In the transport results, it was found that when the magnetic field lies in the [112] or 
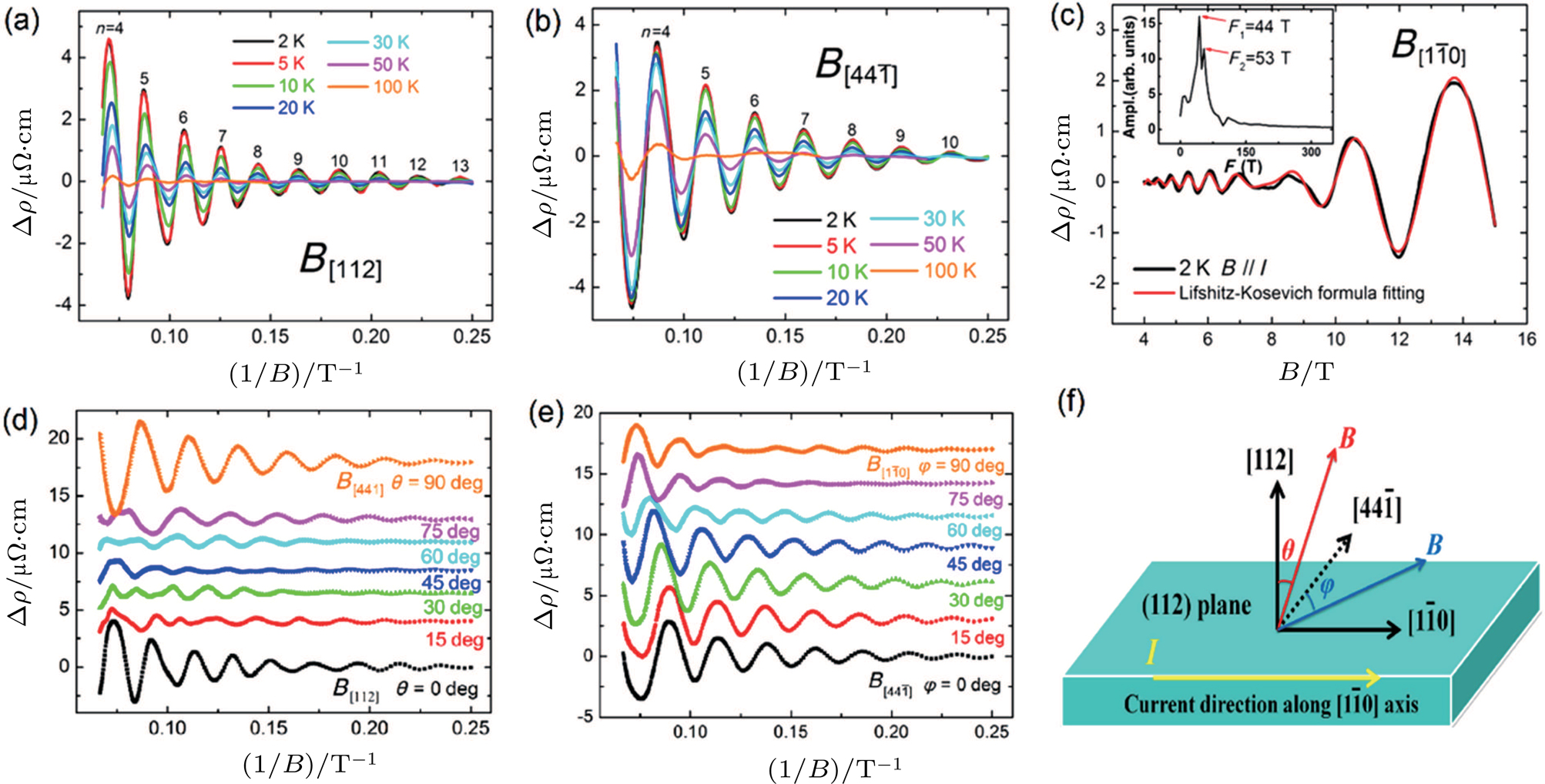 | Fig. 3. (color online) (a)–(c) SdH oscillations in Cd3As2 single crystal at various temperatures when the magnetic field is applied along the [112],  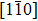 |
| Table 1.
Fast Fourier Transform results of the SdH oscillations in DSM Cd3As2 single crystals under various magnetic field directions.[35] . |
In addition to detect the transport properties of the DSM of bulk Cd3As2, it is also of interest to explore the intriguing physics in low-dimensional DSMs. For example, an oscillating quantum spin Hall effect is expected in the quantum well structure of DSMs, which means that the system shows oscillatory crossover between trivial and nontrivial 2D insulators as a function of the thickness. In addition, the investigations on the low-dimensional DSMs are crucial to the potential nanoelectronic applications. The synthesis of low-dimensional DSM Cd3As2 has been realized, in which Cd3As2 thin films were grown in a molecular beam epitaxy system by directly evaporating the bulk materials onto substrates[95,96] and high quality Cd3As2 microbelts, nanobelts, nanowires, etc. were fabricated by chemical vapor deposition (CVD) method.[97–103]
The transport properties of the Cd3As2 thin films, tuned by an applied gate voltage, thickness or doping, were investigated. In a 50-nm-thick Cd3As2 film, Liu et al. demonstrated a transition from band conduction to hopping conduction via electrostatic doping by solid electrolyte gating.[95] The extreme charge doping also enables an observation of a transition from electron- to hole-dominated two-carrier transport.[103] Besides, Cheng et al. revealed a thickness-induced semimetal-to-semiconductor transition in the single-crystalline Cd3As2 films.[104] In contrast with the metallic behavior in the bulk counterpart, the 50-nm-thick Cd3As2 film exhibits semiconducting characteristics, suggesting a bandgap opening. With the reduced film thickness from 900 nm to 50 nm, a transition from nontrivial to trivial Berry phase was also revealed. Furthermore, Yuan et al. investigated the quasiparticle dynamics and band evolution in Cd3As2 thin films by controlled chromium (Cr) doping.[105] In undoped Cd3As2, the observed square-root-B relation of inter-Landau-level resonance signals the existence of massless Dirac fermions. With the controlled Cr doping, a topological phase transition and Dirac mass acquisition can be achieved, which enables a dynamic control of the quasiparticles.
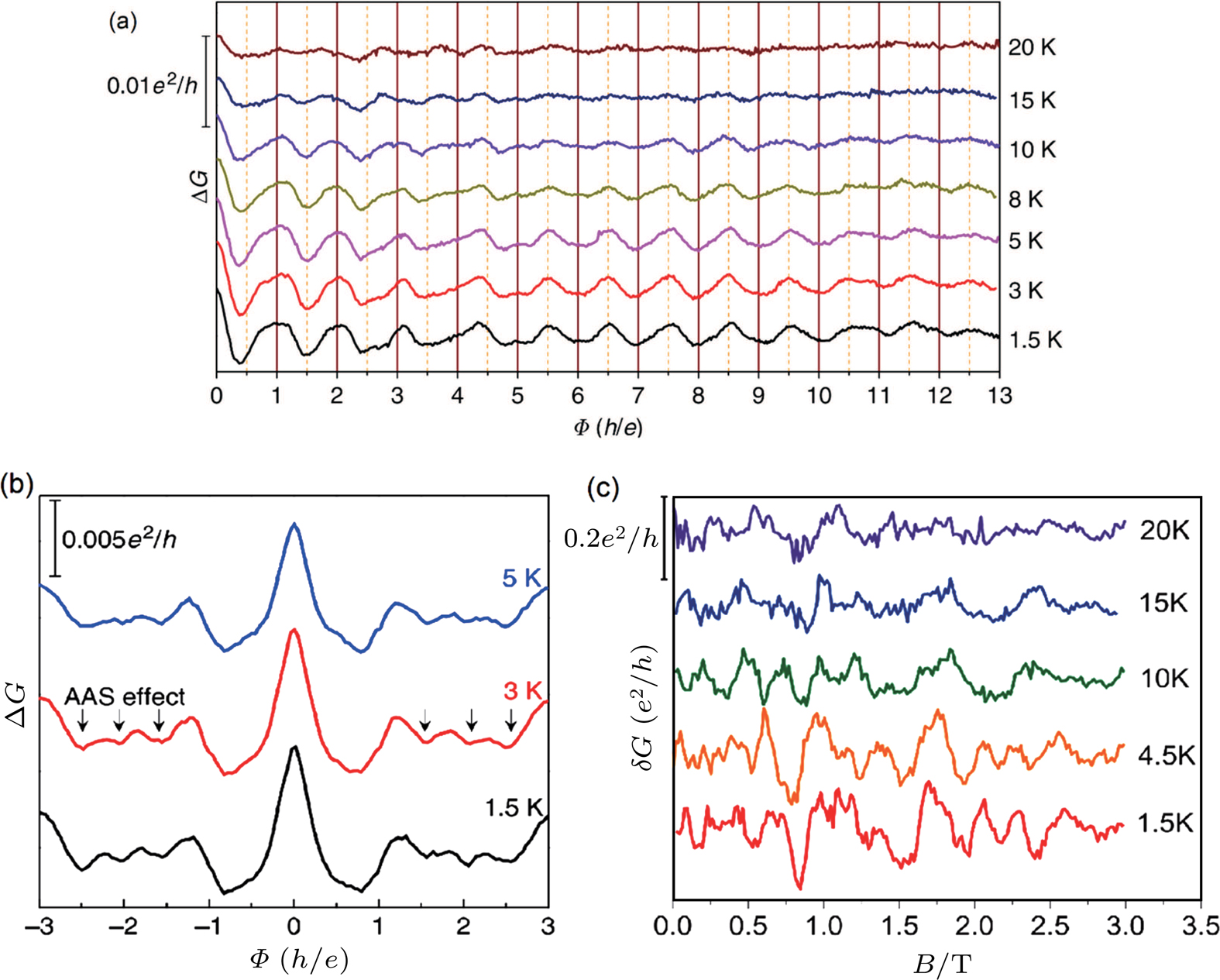
In the low-dimensional Cd3As2 structures, the high quality Cd3As2 microbelts and nanobelts grown by CVD exhibit the metallic behavior similar to the bulk crystal with very high mobility and pronounced SdH oscillations.[98,99] Besides, the semiconducting-like behavior was also observed in the resistance-temperature (RT) characteristic of some mesoscopic Cd3As2 structures, e.g., the thin films, nanowires and microribbons.[95,99–101,108] The semiconducting-like behavior might origin from the bandgap opening due to quantum confinement effect[99] or the low carrier density as the Fermi level is very close to the Dirac point.[100] Particularly, the magnetotransport measurements on the Cd3As2 nanowires reveal glaring quantum interference effects when the samples are scaled down to the phase-coherent region and thus the quantum correction to classical conductance becomes remarkable. Wang et al. reported the Aharonov–Bohm (AB) oscillations, Altshuler–Aronov–Spivak (AAS) oscillations and universal conductance fluctuations (UCF) in individual Cd3As2 nanowires (Fig.
The DSM is on the boundary of various topological phases.[15–17] It means that by modulation, the DSMs can be driven into other topological states, such as TIs, TSCs, WSMs, etc. Theoretically, the presence of a magnetic field would break the TRS and the overlapped WPs in the DSMs may be split into two separated WPs, which indicates a transition from DSMs to WSMs possessing chiral Weyl fermions and FAs. The experimental observation of a large spin-splitting of the conduction band in a magnetic field suggests a removal of spin degeneracy in DSM Cd3As2 by breaking TRS. Combining a band structure model consistent with the results of spin-splitting and extended Dirac-like dispersion, Jeon et al. reported that Weyl fermions might be the low-energy excitations in Cd3As2 when an external magnetic field is applied along the axis of the Dirac points.[32] Cao et al. also demonstrated the possibility of inducing WSM phase in DSM Cd3As2 at high magnetic fields by detecting the Landau level splitting and an angular dependent Berry phase.[109] An unexpected nontrivial Berry phase was obtained in the DSM Cd3As2 in certain measurement configuration when a field-generated mass term could be introduced to the system. Based on the observation, it was suggested that the results might serve as the hints for the emerging Weyl fermions in Cd3As2, where the spin degeneracy is removed by breaking TRS and a WSM phase is further demonstrated.
Chiral anomaly is a phenomenon associated with the chiral Weyl fermions (see more in Subsection 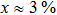
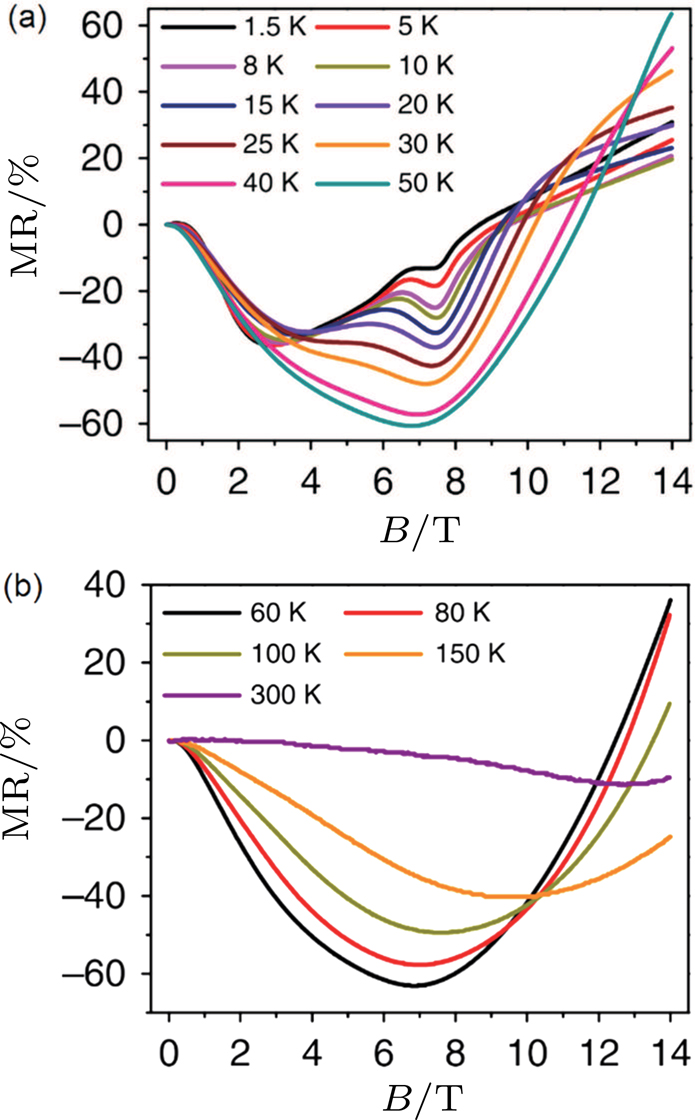 | Fig. 5. (color online) (a) and (b) Negative MR in a Cd3As2 nanowire measured at temperatures from 1.5 K to 300 K.[100] The negative MR was ascribed to the chiral anomaly. |
Besides the appealing chiral anomaly associated with the Weyl fermions, the WSM has disconnected FAs on the surfaces due to the broken translational symmetry. In the presence of a static magnetic field perpendicular to the two opposite surfaces of a WSM, the disjointed FAs from two opposite surfaces can intertwine with chiral bulk modes and develop unusual closed magnetic orbits. A new type of quantum oscillation that arises from such Weyl orbits can in principle be detected.[116] For the DSMs consisting of two superposed copies of WPs, similar quantum oscillations might also occur while there are additional complications that must be considered, e.g. the reduced symmetry of the surfaces, the reduced symmetry in a magnetic field, and their interplay with bulk topology.[116] Experimental evidence for the Weyl orbit was claimed in focused-ion-beam-prepared microstructures of Cd3As2, in which an additional 2D quantum oscillation emerges when the thickness of the sample is comparable to the bulk transport mean free path.[117] However, Kargarian et al. argued that the double FAs in DSM is in fact unstable.[118] In contrast to the FAs in WSM, the doubled FAs in DSMs are not topologically protected in general and can be continuously deformed into a Fermi pocket in the presence of a surface perturbation. Thus, the reported Weyl orbits in DSM Cd3As2 microstructures might be a consequence of the mixing of bulk and surface states.[118] Recently, Zheng et al. suggested an observation of the quantum oscillations associated with such Weyl orbits in Cd3As2 nanoplates.[119] When the thickness of the nanoplates is smaller than the quantum mean free path of the electrons, additional 2D MR oscillations were observed at high magnetic fields to be superimposed on the conventional 3D bulk oscillations. The oscillating frequency of the 2D oscillations is close to the theoretical calculation of the Fermi-arc oscillation frequency. Thus, the discovery was ascribed to the manifestation of the Weyl magnetic orbits connecting the open FAs from opposite surfaces. Moreover, further evidence detected by the nonlocal transport measurements was also presented in the work to unveil the transport properties of FAs in TSMs. The 2D surface transport in the DSM Cd3As2 was also studied by Zhang et al. based on a series of Cd3As2 nanoplates.[120,121] In the selected different samples with lowering Fermi level, it was found that the contribution from bulk oscillations decreases and the surface state transport dominates gradually at the perpendicular magnetic fields. With further increasing magnetic fields, the system was driven into an unconventional quantum Hall state,[120,121] which was also observed in thin films of the DSM Cd3As2.[122,123] The origin of the quantum Hall effect and its relation to the Weyl orbits are calling for further investigations.
The DSMs can be driven to many other phases by breaking certain symmetries, in which the topological phase transition from a DSM to a WSM has been introduced.[32,105] Besides, a very attracting topic arises from the possible transition from a DSM to a TSC.[1,2,124,125] TSCs show a superconducting gap in the bulk state, but support gapless Majorana fermions or Majorana zero modes in the boundary.[126–129] The Majorana zero modes obey non-abelian statistics, and can be applied to topological quantum computation and to build a fault-tolerant quantum computer.[130,131]
In 2016, Wang et al. discovered superconductivity induced by hard point contact (PC) on DSM Cd3As2 crystals (Fig. 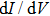
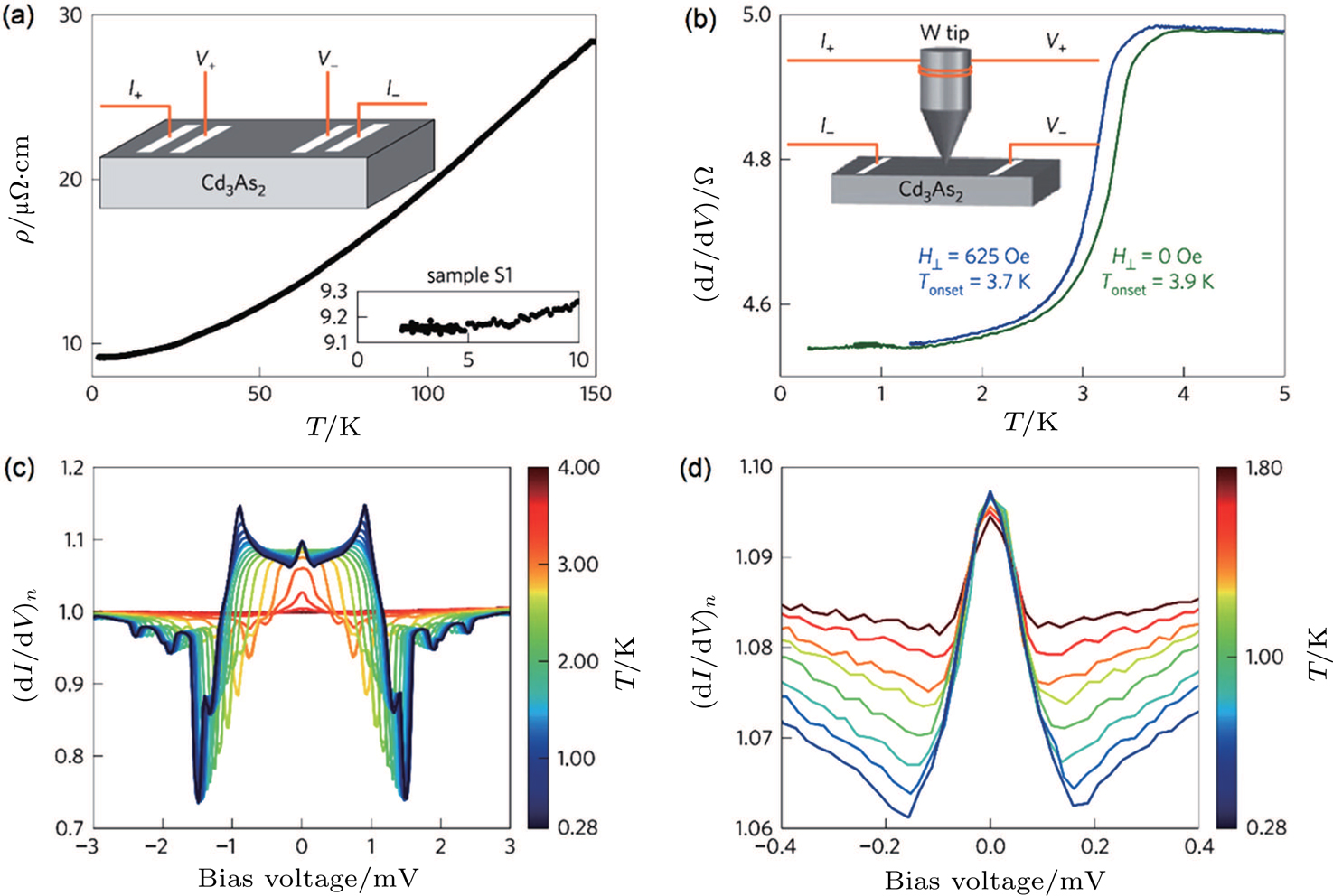 | Fig. 6. (color online) (a) RT characteristic of the bulk Cd3As2. Upper Inset: Schematics of the standard four-probe method measurement configuration. Lower inset: Zoom-in of the RT curve below 10 K. (b) Temperature dependence of the zero-bias PC resistance. Inset: Schematics of the PCS measurement configuration. (c) Normalized  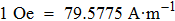 |
The PC measurement was previously used to study superconducting materials and get the information of superconductivity.[134,135] In Wang et al.’s work, the hard PCS technique has been developed to induce superconductivity on non-superconducting topological materials by using non-superconducting tip (hard PC), different from previous PC experiments on superconductors. More importantly, the results reveal a new way to detect and study TSCs, which is different with the prevailing proximity effect method on superconductor-TI (spin–orbit coupling semiconductor) hybrid structures for creating topological superconductivity or Majorana fermions.
The exotic discovery of the superconductivity in DSM Cd3As2 promptly attracted attentions from both theorists and experimentalists. The suggestion that the pressure and doping induced by the hard tip may be the origin of the superconductivity in Cd3As2 was further confirmed by a later experimental work. He et al. presented the resistance measurements on Cd3As2 single crystals under pressure up to 50.9 GPa.[136] With the increasing pressure, the low temperature resistance of Cd3As2 firstly increases while finally decreases when the pressure is above 6.4 GPa. Superconductivity appears at 8.5 GPa with a T c of about 2.0 K. The T c keeps increasing to about 4.0 K at 21.3 GPa, then shows nearly as a constant up to the highest pressure 50.9 GPa. In addition, it is noted that another group also studied the polycrystalline Cd3As2 by hard PC measurements and observed the indication of superconductivity.[137]
Besides the Cd3As2 system, the properties of DSM were also explored in many other materials, such as Na3Bi,[31,138,139] PtBi2,[140] and Zr(Hf)Te5.[141–164] The theoretical prediction of Na3Bi as a DSM was presented in 2012,[15] and soon the experimental results from ARPES confirmed the 3D DSM state in Na3Bi.[17] The Na3Bi material is incredibly unstable upon exposure to air and moisture, which hinds the wide investigations on this system. Nevertheless, using special care to prepare the samples, Xiong et al. revealed the chiral anomaly[31] and the anomalous conductivity tensor[138] in the DSM Na3Bi. In addition, Hellerstedt et al. grew large-area thin films of Na3Bi and investigated the electronic properties by back gating method.[139]
The hunt for new natural DSM materials with novel properties has been an important issue since the successful discovery of DSM Cd3As2 and Na3Bi. Gibson et al. predicted a series of compounds as the DSM candidates,[39] which includes the Pyrite-type PtBi2. Gao et al. synthesized high-quality PtBi2 single crystals and carried out detailed magnetotransport measurements.[140] They observed an extremely large unsaturated MR up to 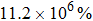
The DSM state was also studied in topological nontrivial Zr(Hf)Te5,[141–167] a layered material with van der Waals coupling between individual layers. The compound was initially studied for its resistivity anomaly, thermoelectric properties and quantum oscillations.[168–174] The second study wave was ignited by the ab initio theoretical prediction that HfTe5 and ZrTe5 crystals are located near the phase boundary between weak and strong TIs.[141] Li et al. investigated the ZrTe5 single crystals by the ARPES technique, which revealed that the electronic structure of ZrTe5 was consistent with a 3D DSM.[142] Moreover, obvious negative longitudinal MR was observed in ZrTe5 when the magnetic and electrical fields were parallel. The NMR was suggested to arise from the chiral anomaly in the DSM ZrTe5,[142] and the discovery further stimulated intensive studies.[143–164] Chen et al. reported the linear rising of the optical conductivity in a relatively large energy scale expected for a 3D DSM.[143] They also presented a magnetoinfrared spectroscopy study, in which the transitions between Landau levels and their field dependence were quantitatively consistent with the 3D massless Dirac fermions.[144] Besides, it was found the QL regime can be realized by a very small magnetic field (about 1 T) in the ZrTe5 samples. Moreover, the observation of the splitting of the Landau levels was suggested as a transition in ZrTe5 from a DSM to an NLSM.[144]
The transport properties of ZrTe5 were then provided by a lot of research work.[145–161] In ZrTe5 nanoribbons exfoliated from bulk crystals, Zheng et al. presented exotic properties including the NMR at 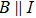
The pressure-tuned properties of ZrTe5 were also investigated. Superconductivity was induced in the DSM ZrTe5 under the high pressure generated by a screw-pressure-type diamond anvil cell.[150] The superconductivity appears above 6.2 GPa with the critical temperature T
c increasing with applied pressure and reaching a maximum of 4.0 K at 14.6 GPa. At pressures above 21.2 GPa, the phase coexists with a second superconducting phase with the maximum T
c of about 6.0 K. Furthermore, it was found the observed two-stage superconducting behavior closely related to the structural phase transition under the pressure. The hydrostatic pressure shows different influence on the magnetotransport properties of ZrTe5.[151] With increasing pressure, the magnetoresistance in the case of 
Though intensive experimental investigations support the DSM state in ZrTe5, the evidences for identifying ZrTe5 as a weak TI or a strong TI were also reported.[161–166] For example, the scanning tunneling microscopy suggested that the ZrTe5 crystal as a weak 3D TI.[161,162] In fact, based on the recent intensive research from both theorists and experimentalists, it is known the ZrTe5 material is extremely sensitive to the cell volume[167] and thus the measured physical properties, such as the resistance–temperature characteristic, the MR effect and the Hall information are divergent.[145–161] Impurities/nonstoichiometry, defects, and strain may affect the cell volumes, which are closely related to the growth condition of the samples. Thus, the Zr(Hf)Te5 can manifest as a strong TI, a DSM, or a weak TI under variant crystal volumes, which depends on the sample quality.[167] Useful information for understanding the divergent bulk properties can be obtained from the investigations on ZrTe5 nanosheets with different thickness,[153,154] which also indicate a very sensitive band structure of ZrTe5.
As a sister compound of ZrTe5, HfTe5 has been rarely studied experimentally. Wang et al. presented the first electrical transport evidence for the chiral anomaly and the ultrahigh mobility in HfTe5 crystals (Fig. 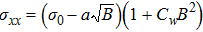
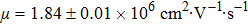
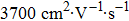
 | Fig. 7. (color online) (a) Quantitative fitting for the NMR in HfTe5 when 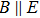 |
Beyond the above DSM systems with normal Dirac nodes in the momentum space, the type II DSM PtTe2 with titled Dirac nodes was also identified recently.[179] Yan et al. studied the bulk PtTe2 single crystal and revealed a pair of strongly tilted Dirac cones by the combined ARPES measurements and first-principles calculations, which confirmed PtTe2 as a DSM with the Lorentz-violating type-II Weyl/Dirac fermions.[180] The work paves way for further investigating novel quantum phenomena and topological phase transition in the new TSM sates.
In WSMs, the Weyl nodes with different chirality are separated in momentum space. In parallel electric and magnetic fields (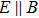
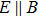
The first discovery of 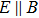
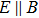
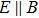
The clear identification of Weyl nodes in TaAs crystals paves the way for the exploration of chiral anomaly. Huang et al. reported an NMR in the characterized WSM TaAs when the external magnetic and electrical fields are parallel.[] The NMR shows sharp dependence on the angle between the electric and magnetic fields and can be well fitted by the chiral anomaly formula, which was recognized as the signature of the expected chiral anomaly. At almost the same time, Zhang et al., presented the evidence of chiral anomaly in TaAs by showing the unique features of the NMR (Fig.
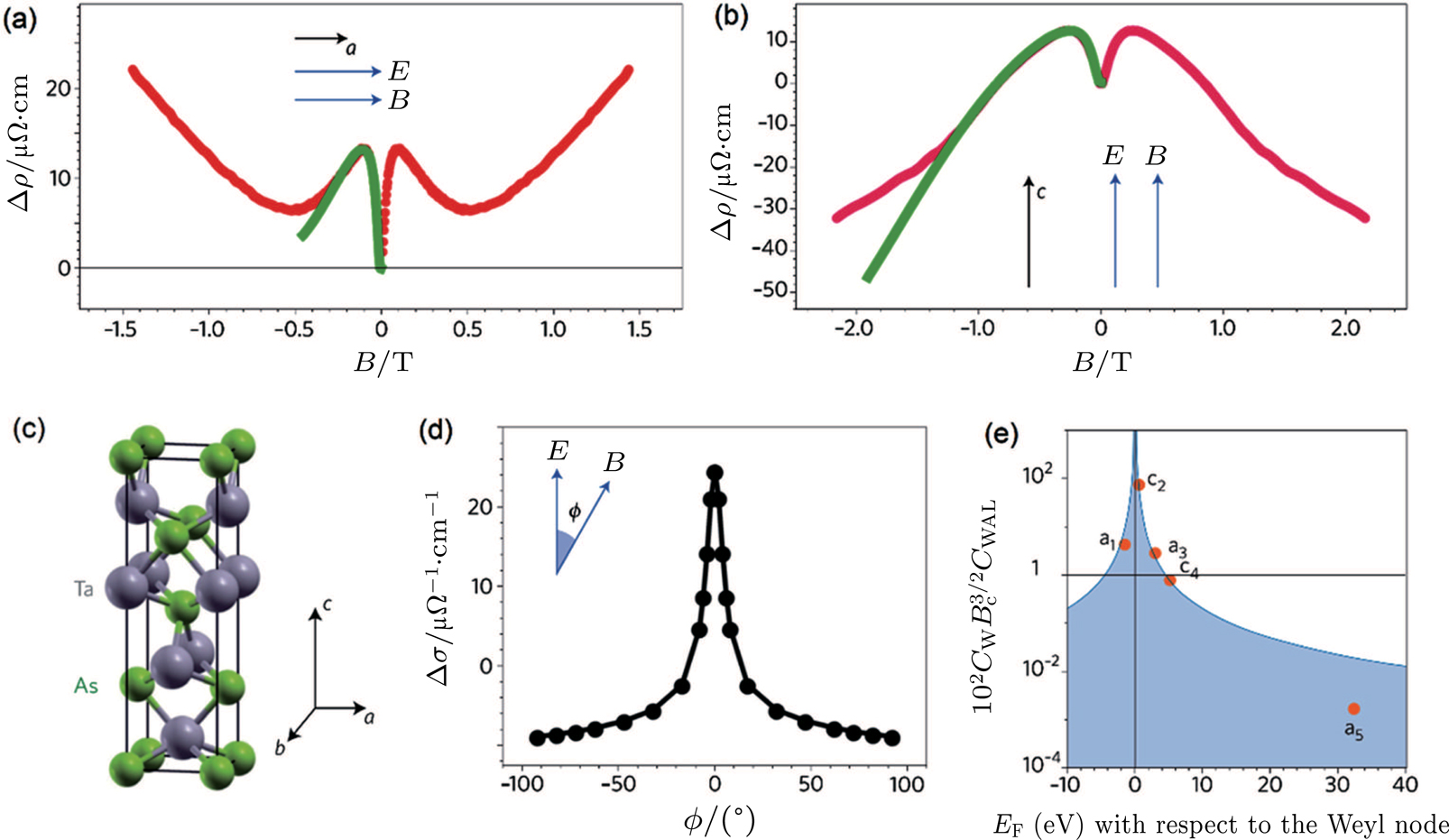 | Fig. 8. (color online) (a) and (b) Negative MR in TaAs. Red lines are experimental data and green lines are theoretical fits. a and c are the lattice vectors. (c) The tetragonal crystal lattice of TaAs. (d) MR data as a function of the angle between the electric and magnetic fields. (e) Dependence of the chiral coefficient on chemical potential E F.[86] |
The magnetotransport measurements also demonstrate other intriguing properties of WSM TaAs, such as the giant MR embedding with obvious SdH oscillations, nontrivial Berry phase, and ultrahigh mobility. Zhang et al. reported that the bulk TaAs exhibits an extremely large, unsaturated linear MR with a magnetic field perpendicular to the current.[60] The MR reaches 5.4×105% at 10 K in a magnetic field of 9 T and 2.47×106% at 1.5 K in a magnetic field of 56 T. Besides, the Landau fan diagram of the superimposed SdH oscillations on the MR shows the nontrivial Berry phase close to π. Due to the semimetal property of TaAs, both hole and electron carriers exist in the system, which usually induces the observation of nonlinear Hall behavior. The nonlinear Hall trace can be analyzed by a two-carrier model to reveal the carrier information. Zhang et al. showed that TaAs manifests an ultrahigh carrier mobility 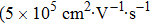
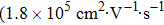
Since the FSs of WSMs usually are small, it is achievable to reach the QL in available magnetic fields.[183–187] When the electrons are driven into the lowest Landau level in an intensive magnetic field, anomalous features in the ultraquantum regime were reported in WSMs.[183–187] Zhang et al. reported the electrical transport properties of WSM TaAs in magnetic fields up to 55 T.[183] Additional oscillatory structures were observed in the longitudinal MR and Hall traces beyond the QL of TaAs at low temperatures (Fig.
 | Fig. 9. (color online) (a) The longitudinal MR of TaAs with respect to the inverse field at 1.5 K.[183] (b) The MR and Hall of TaP in ultrahigh magnetic fields.[187] Anomalous features occur in the ultraquantum regime of the WSMs above the QL. |
In topologically trivial conductors, the magnetization tends to a saturation at the QL, which was commonly observed in low carrier density semiconductors e.g., InSb and InAs.[188] In WSMs, however, the collapse of the magnetization leads to a magnetic anomaly.[186] In the magnetic torque measurements on WSM NbAs, a sharp anomaly, the sign change of the magnetic torque, was reported upon reaching the QL in high magnetic fields. The observation of crossover from diamagnet below the QL to paramagnet above the QL was attributed to the topological nature of the Weyl electrons.[186]
Upon approaching and surpassing the QL, the WSM TaP also presents a series of anomalous structures in the magnetic torque and electrical transport measurements, which were ascribed to the multiple field-induced phase transitions.[184] Zhang et al. studied the magnetic tunneling of the lowest Landau bands in TaP,[187] which indicates the hybridization of adjacent Fermi pockets. To observe the magnetic tunneling of the lowest Landau level, the QL should be reached and the separation of pockets in k space cannot be far. In the high-field measurements, Zhang et al. observed a sharp sign reversal in the Hall resistivity at a magnetic field located inside the ultraquantum limit. The magnetic field corresponds to the separation of the W1 Weyl nodes in momentum space, which reveals the magnetic coupling between the electron pockets arising from the W1 Weyl fermions. The findings in the ultraquantum regime provide evidences for the magnetic-field-induced gap opening of the chiral Landau levels and the unique Weyl node annihilation in the WSM.[187]
The fertile phenomena observed in the ultraquantum WSMs shows that the QL is a promising regime for finding new states of matter based on the Weyl fermions.[189] Thus, the related investigations in future may bring more interesting discoveries in this direction. On the other hand, though possible mechanisms of features in the ultraquantum regime of WSMs have been argued, further investigations are still necessary to conclusively identify the exact underlying nature.
As introduced in Subsection
In 2016, Wang et al. reported unconventional superconductivity induced by hard PC on 3D DSM Cd3As2 crystals (more details in Subsection
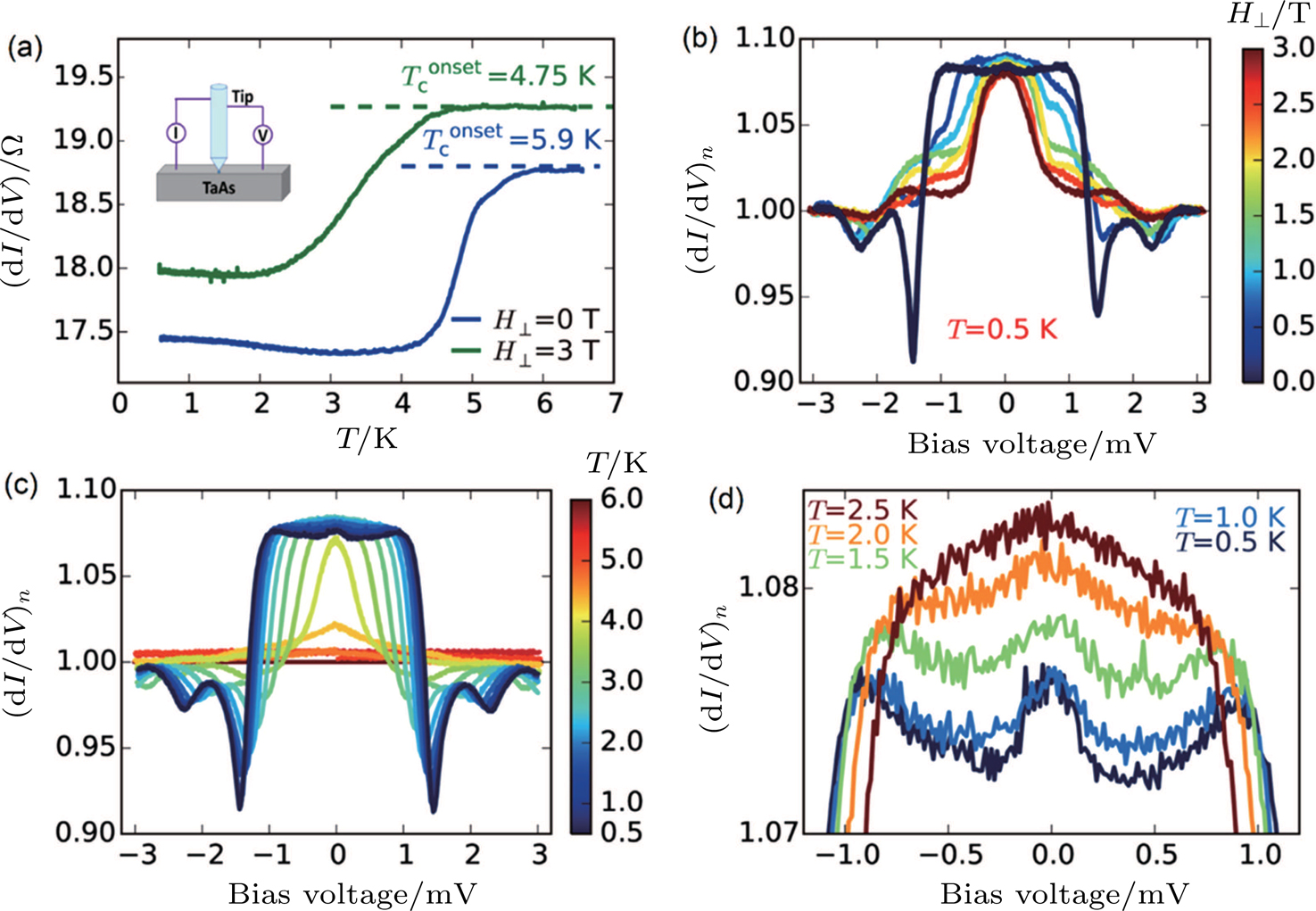 | Fig. 10. (color online) (a) Temperature dependence of PC resistance showing superconducting signal. Inset: schematics of the PCS measurement configuration. (b) Normalized   |
The hard PC results of the WSM TaAs indicate that the local “uniaxial” pressure and doping effect around PC region may be important to the appearance of superconductivity. The high-pressure experiment on TaAs was also reported.[191] At a pressure around 14 GPa, it was predicted that TaAs might show a new WSM phase, which has 12 WPs at the same energy level rather than the 24 WPs distributed at two energy levels.[191] Experimental results consistent with the new hexagonal P-6m2 phase at pressure were provided by the electrical transport measurements and Raman spectroscopy. Besides, the P-6m2 phase was suggested to be kept to ambient pressure. However, no hint of superconductivity appears down to 1.8 K until 54.0 GPa in this high-pressure work.[191]
By doing resistance measurements on the WSM TaP under pressure up to about 100 GPa, Li et al. observed the superconductivity in TaP at about 70 GPa.[64] The superconductivity retains when the pressure is released. Their calculations based on the density functional theory illustrate a structure transition of TaP at about 70 GPa, which may be the underlying origin of superconductivity. The discovery of superconductivity in WSMs TaAs and TaP mentioned above will stimulate further study on the superconductivity in WSMs and offer a new platform to search for TSCs. Especially for the tip-induced superconductivity on TaAs, it might be interface superconductivity and the FA surface states may contribute a lot since both tip and sample are non-superconducting and the surface state carrier is easier to be modulated by tip to form superconducting Cooper pairs. Further theoretical and experimental investigations are highly desirable to classify this new topic.
TaAs family are the most studied WSMs while the TaAs family are only on behalf of one type of WSMs, known as type-I WSMs. WSMs can be further classified into type-I WSMs and type-II WSMs based on whether the Weyl cones are titled or not (Fig.
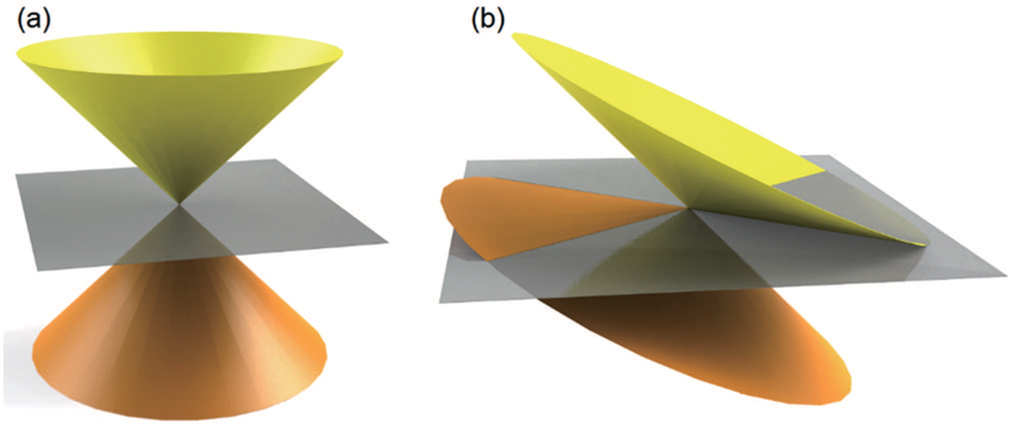 | Fig. 11. (color online) (a) The Weyl cone in type-I WSMs. (b) The Weyl cone in type-II WSMs. The grey planes correspond to the position of the Fermi level. |
Theoretically predicted type-II WSM MoTe2 was recently confirmed by showing direct spectroscopic evidence of topological FAs in the ARPES results.[193–200] The type-II WSM MoTe2 is found to be superconducting around 0.1 K[201] and the doped MoTe2 can show higher T
c.[202] Li et al. grew MoTe2 crystals by partially substituting Te with S to enhance the superconducting onset temperature and observed nontrivial superconducting signatures in this topological material.[203] By scanning tunneling spectroscopy measurement, they firstly observed the quasiparticle interference patterns of FAs at the surface of MoTe2−xSx crystal, which are consistent with the calculated nontrivial band structure. They also detected a relatively large superconducting gap (Δ) on the sample surface, which shows a large 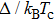
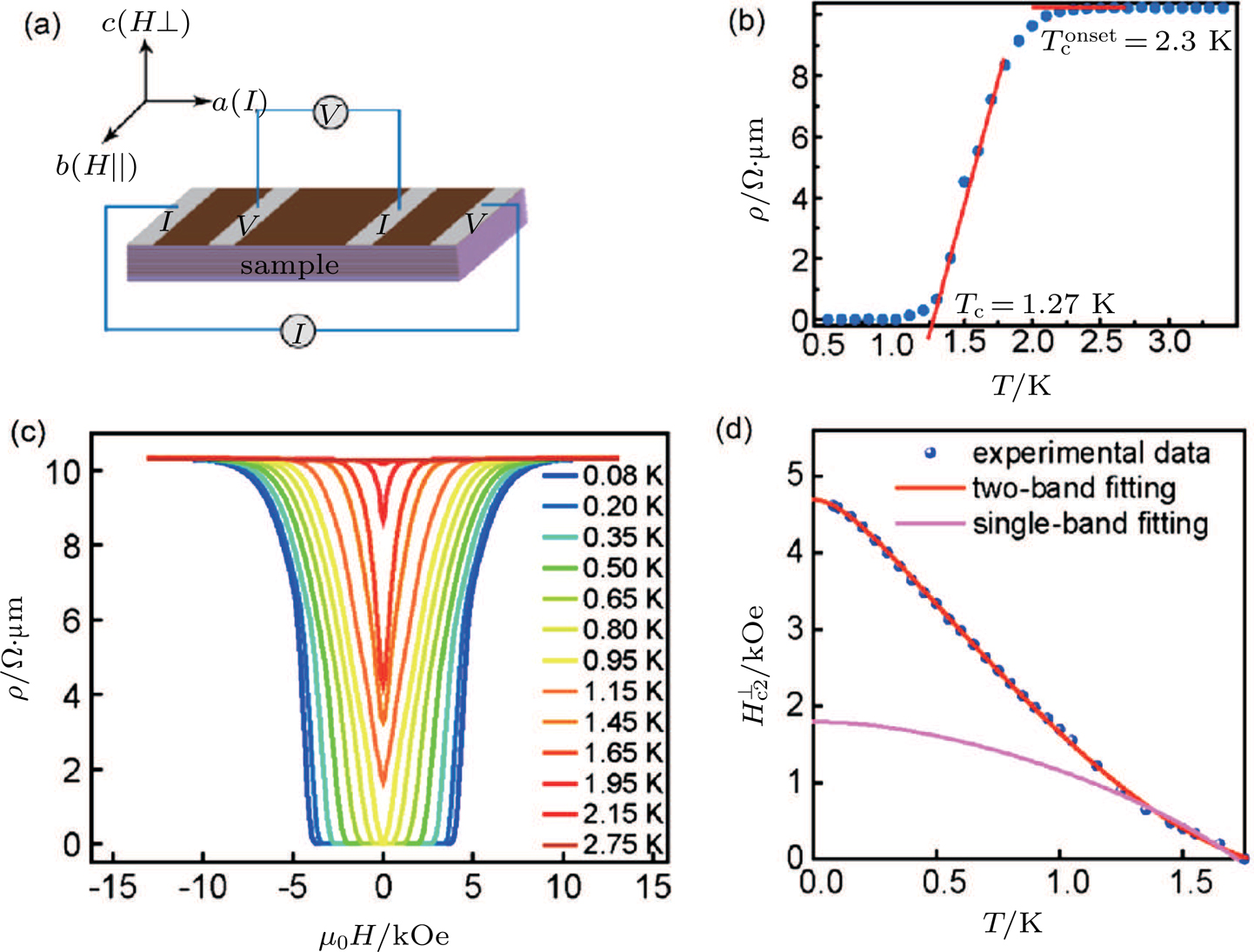 | Fig. 12. (color online) (a) Schematic diagram for magnetotransport measurements of MoTe2−xSx. (b) Typical resistivity–temperature curve of MoTe2−xSx showing superconductivity. (c) MR at various temperatures under perpendicular field. (d) Temperature dependence of 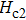 |
WTe2, a semimetal which was studied intensively in the past years due to the large MR,[205–212] was also predicted to be a type-II WSM.[192] Spectroscopic evidence on the type II WSM WTe2 has been provided by ARPES experiments while the FAs are hard to be clearly resolved.[213] Moreover, significant anisotropic chiral anomaly effect of the type-II WSM has been observed in the WTe2 thin films and the Fermi-level delicately adjusted WTe1.98 crystals by performing systematic magnetotransport studies.[214,215]
An additional subclass of WSM materials is the so-called multi-WSMs.[216] The monopole charge of a Weyl point is equal to the number of Berry fluxes passing through a closed surface enclosing the target Weyl point only. So far, most studies on WSMs have focused on the case with the lowest monopole charge, C = ±1, such as the TaAs family. The Weyl point in multi-WSMs carries topological charges of higher magnitude, for example, HgCrSe2 and SrSi2 are the so-called double WSM candidates with C = ±2 predicted by the calculations.[217,218] Such higher-charge Weyl points may be stabilized by certain point group crystal symmetries, and more interesting effect may appear. For instance, it is pointed out by theory that WPs with higher monopole charge exhibit anisotropic screening to the Coulomb interactions.[219,220]
In this chapter, we have mainly introduced the transport properties of DSMs and WSMs in magnetic fields. It is noted that the TSMs, either WSMs or DSMs, show many features in common, such as the large MR, the ultrahigh mobility, and the remarkable quantum oscillations. On the other hand, we can see that each TSM system also possesses its unique property, such as the nested Fermi surface of Cd3As2 and the low QL of TaAs. In this view, the many other predicted materials still deserve experimental identifications and more intriguing phenomena can be expected in those new TSM materials.[11] In addition, the exploration of new type of TSMs is also a significant issue in this field. As is known, the currently studied DSMs Cd3As2 and Na3Bi possess a pair of DPs while the WSM TaAs family have 12 pairs of WPs. The large number of the DPs or WPs may hinder a direct investigation and understanding of the properties of TSMs. Thus, the TSMs with the simplest WPs are desirable. Besides, for the precise demonstrations of the characteristic of Weyl fermions, the TSMs with ideal Fermi level very close to the nodes and no other states at it are highly expected. So far, most investigated WSM materials are inversion symmetry broken systems, the search for magnetic WSM materials with broken TRS is very important direction too.[221] It is noted that signature of the existence of Weyl fermions has been reported in magnetic Heusler GdPtBi.[222] The great diversity of Heusler compounds with more than 1500 members may establish an opportunity to enlarge the TSM family.[223] Besides, the recent discovery of magnetic topological semimetal states in Sr1−yMn1−zSb2 (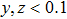
In fact, both Dirac and Weyl fermions can be considered as special cases of the multifold fermions.[226] Due to the two/four-fold degeneracies at high-symmetry points, Weyl/Dirac quasiparticles are thus two/four-fold fermions within the multifold-fermion scenario. In solid-state systems with spin-orbit coupling and with certain symmetries, new types of symmetry–protected fermions arise by possessing three-, six- and eight-fold degeneracies at and along high-symmetry points, lines and surfaces. In analogous to Dirac/Weyl semimetals, emergent phenomena, e.g., Weyl points, FAs, Fermi drums and chiral anomaly, can be expected in the multifold-fermion systems. First-principles calculations have predicted several candidate materials that might host the exotic multifold-fermionic quasiparticles,[226–229] e.g., Ag3AuSe2, Ba4Bi3, MgPt, CuBi2O4, θ-TaN, WC-type ZrTe, etc. Very recently, the scientists from IOP china have reported the ARPES experimental signatures of the triply degenerate point in the electronic structure of crystalline MoP and WC.[230,231] Lv et al. observed the three-component fermions in the bulk of MoP, which is well consistent with the theoretical results.[230] Moreover, the triply degenerate points were also discovered by Ma et al. in high quality WC, in which the nodal points were near the Fermi level and the exotic properties related to the three-component fermions could be detected more clearly.[231] Importantly, they further observed FA topological surface states connecting to the surface projections of the triply degenerate nodal points, which suggested nontrivial topology of the semimetal state.[231] In addition, the electrical transport properties of the new type of semimetals were investigated. He et al. found the NMR phenomenon in WC can only appear for certain direction when the magnetic field was parallel to the current,[232] and Shekhar et al. reported extremely low resistivity in MoP,[233] which may be related to the exotic triple point fermions.
As introduced in the above, topological superconductivity is a hot topic in condensed matter physics. Previous experimental explorations are mainly focused on TI (spin–orbit coupling semiconductor)-superconductor hybrid structures. The discovery of TSMs offers new and ideal platforms to study the topological superconductivity due to the naturally nontrivial topology. Particularly, the superconductivity has been observed in some DSMs and WSMs, while the topology of the superconductivity still needs more theoretical and experimental efforts to fully illustrate the issue. Moreover, the hard PC method has been developed as a new and effective way to induce superconductivity on non-superconducting TSMs,[132] which significantly expands the research subjects. We expect that the topological superconductivity could be finally confirmed by this new method combing with other experimental techniques and pave the way for future topological quantum computing.
As the Fermi levels of type-I WSMs and DSMs are at or near the discrete Weyl nodes, it is expected that these systems would usually show small carrier density and small QL. For example, the QL of TaAs can be about 8 T[60] and the QL of ZrTe5 can be below 1 T.[144,148] Thus, the ultraquantum regime has now been an achievable territory to be exploited. For example, anomalous features were reported in the ultraquantum regime of WSM TaAs and TaP. Though experimental results are obvious and distinct, the full understanding of the exotic phenomena still needs more investigations from theorists and experimentalists in the future. Moreover, the very small carrier density system may be recognized as an electron gas system and the few-body and many-body effect would be rather relevant. Thus, more interesting phenomena are expected to be revealed in the ultraquantum regime of TSMs.
TSMs not only show unique properties in the electrical transport behaviors but also bring surprising phenomena in the optical and thermal measurements.[234–240] For example, DSM Cd3As2 not only processes advantages of graphene as a photosensitive material but also shows great potential to realize either an ultrafast broadband photodetector or an ideal ultrafast switch in mid-infrared lasers and photonics.[236–238] Besides, a negative magneto-thermopower possibly induced by the chiral anomaly is observed in thermopower measurements when the magnetic field is parallel to the temperature gradient and the quadratic coefficient is found nearly twice of that for the electrical conductivity.[239] Furthermore, the electron or hole doping in DSM Cd3As2 largely improves the optimum figure of merit, which shows a great potential for the high performance of thermoelectric applications.[240]
The experimental confirmations of the DSM and WSM were initially realized in 2014 and 2015, respectively. Though great progress has been made in this field, in fact, the current investigations are only the tip of an iceberg. More classes of DSMs, WSMs, and other types of TSMs are waiting to be uncovered. Further efforts are needed to be devoted to discovering new alluring phenomena in these unique systems and to revealing the underlying physics, which would pave the way for the understanding and potential applications of the materials in topological world. Significant breakthroughs are expected to be generated in this rapidly developing field, wherein the application of high magnetic fields definitely is one of the most powerful methods.
We acknowledge Yanzhao Liu for the help in the preparation of this work.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] | |
| [114] | |
| [115] | |
| [116] | |
| [117] | |
| [118] | |
| [119] | |
| [120] | |
| [121] | |
| [122] | |
| [123] | |
| [124] | |
| [125] | |
| [126] | |
| [127] | |
| [128] | |
| [129] | |
| [130] | |
| [131] | |
| [132] | |
| [133] | |
| [134] | |
| [135] | |
| [136] | |
| [137] | |
| [138] | |
| [139] | |
| [140] | |
| [141] | |
| [142] | |
| [143] | |
| [144] | |
| [145] | |
| [146] | |
| [147] | |
| [148] | |
| [149] | |
| [150] | |
| [151] | |
| [152] | |
| [153] | |
| [154] | |
| [155] | |
| [156] | |
| [157] | |
| [158] | |
| [159] | |
| [160] | |
| [161] | |
| [162] | |
| [163] | |
| [164] | |
| [165] | |
| [166] | |
| [167] | |
| [168] | |
| [169] | |
| [170] | |
| [171] | |
| [172] | |
| [173] | |
| [174] | |
| [175] | |
| [176] | |
| [177] | |
| [178] | |
| [179] | |
| [180] | |
| [181] | |
| [182] | |
| [183] | |
| [184] | |
| [185] | |
| [186] | |
| [187] | |
| [188] | |
| [189] | |
| [190] | |
| [191] | |
| [192] | |
| [193] | |
| [194] | |
| [195] | |
| [196] | |
| [197] | |
| [198] | |
| [199] | |
| [200] | |
| [201] | |
| [202] | |
| [203] | |
| [204] | |
| [205] | |
| [206] | |
| [207] | |
| [208] | |
| [209] | |
| [210] | |
| [211] | |
| [212] | |
| [213] | |
| [214] | |
| [215] | |
| [216] | |
| [217] | |
| [218] | |
| [219] | |
| [220] | |
| [221] | |
| [222] | |
| [223] | |
| [224] | |
| [225] | |
| [226] | |
| [227] | |
| [228] | |
| [229] | |
| [230] | |
| [231] | |
| [232] | |
| [233] | |
| [234] | |
| [235] | |
| [236] | |
| [237] | |
| [238] | |
| [239] | |
| [240] |