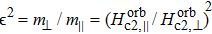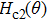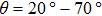Superconductivity with peculiar upper critical fields in quasi-one-dimensional Cr-based pnictides
1. IntroductionSuperconductivity is an intriguing macroscopic quantum state in solids due to the condensation of electronic Cooper pairs. In a phonon-mediated BCS-type conventional superconductor, the superconducting order parameter is mostly of an s-wave in which the underlying Cooper pairs are in a spin-singlet state. In a so-called unconventional superconductor, however, the electron pairing interaction is basically non-phonon-mediated and, the superconducting order parameter is mostly of a non-s-wave, which breaks additional symmetries apart from the global U(1) gauge symmetry.[1] If the Cooper pairs are of spin triplet, which is analogous to those in 3He superfluid phases, the superconductor is always considered as being unconventional. Nonetheless, such a spin-triplet superconductor appears to be rare. Up to 2014, the main candidates of spin-triplet superconductors include some organic superconductors,[2,3] UPt3,[4,5] Sr2RuP4,[6] and U-based superconducting ferromagnets.[7] Note that the superconducting transition temperature Tc of these superconductors is relatively low (below 1.5 K), which is undesirable for in-depth investigations.
Following the discovery of superconductivity at ∼ 2 K under an external pressure of ∼ 1 GPa in CrAs,[8,9] quasi-one-dimensional (Q1D) Cr-based arsenides A2Cr3As3 (A = K, Rb, and Cs) were discovered in 2015.[10–14] The superconducting transition temperature Tc is 6.1, 4.8, and 2.2 K, respectively, for A = K, Rb, and Cs. The normal-state ρ(T) behavior is very different for polycrystalline and single-crystalline samples, primarily because of the anisotropy (see below). The polycrystalline samples show somewhat linear temperature dependence of resistivity [Fig. 1(a)]. In contrast, for high-quality crystals of K2Cr3As3, the normal-state ρ(T) below 50 K follows a power-law relation with an exponent close to 3 [Fig. 1(b)]. The Tc value of high-quality crystals is also increased a little, compared with that of the polycrystalline samples. The defect/impurity effect on Tc can be seen elsewhere,[15] which shows substantial suppression of superconductivity due to nonmagnetic scattering, suggestive of a non-s-wave pairing in K2Cr3As3.
Note that the Tc value increases monotonically with the decrease of ionic radii of the alkali-metal elements, which implies that Tc could be further increased if K+ ions are replaced with smaller cations such as Na+ and Li+. Whereas high-temperature synthesis of these target compounds were unsuccessful,[14] very recently, it was reported that the expected sister compound Na2Cr3As3 could be obtained through an ion-exchange process.[16] The Tc value was indeed increased (up to 8.6 K). This finding further corroborates that Tc increases with decreasing the a axis (interchain distance), as shown in Fig. 2. Interestingly, the Sommerfeld coefficient, derived from the specific-heat measurements, follows a similar dependence.[14]
If the increase of Tc above is considered as a consequence of chemical pressure, then the effect of physical pressure is surprisingly in an opposite tendency. Earlier preliminary data show that Tc of K2Cr3As3 decreases at a rate of −0.34 K/GPa under hydrostatic pressures up to 0.7 GPa.[17] Later high-pressure measurements together with crystal-structure investigations were done for both K2Cr3As3 and Rb2Cr3As3.[18] The result indicates that Tc decreases almost linearly to below 2 K and, by extrapolation, superconductivity disappears at about 8 GPa and 6 GPa, respectively, for K2Cr3As3 and Rb2Cr3As3. A similar result was independently reported for K2Cr3As3.[19] In-situ structural determinations reveal that the extent of non-centrosymmetry, defined by the difference between bond angles of As2–Cr2–As2 (α) and As1–Cr1–As1 (β), seems to be in relation with superconductivity. Note that for the centrosymmetric non-superconducting 133 series ACr3As3 (A = K, Rb, Cs),[20,21] the (α−β) value becomes zero since there is only one Cr site.
Dramatically, Ren and co-workers[22] recently reported that the 133-type KCr3As3 could superconduct at 5 K provided it was in single crystalline form. Additionally, the same group observed superconductivity at 7.3 K in RbCr3As3 single crystals.[23] The Tc value of the latter case is significantly higher than that of Rb2Cr3As3 (4.8 K), which basically rules out the possibility that superconductivity may come from Rb2Cr3As3 that resides in the sample. So far, however, it is not clear whether CsCr3As3 and NaCr3As3 crystals superconduct or not.
Before ending this section, we introduce efforts on explorations of superconductivity in quasi-two-dimensional (Q2D) Cr-based systems. Actually, it was the attempt to look for superconductivity in “Ba1−xKxCr2As2” that led to the discovery of the Q1D K2Cr3As3 superconductor.[14] Along this line, we also discovered Sr2Cr3As2O2[24] and Ba2Ti2Cr2As4O,[25] unfortunately, neither of them are superconducting above 1.8 K. Some theoretical studies predict that doped Q2D Cr-based pnictides could host unconventional superconductivity.[26,27] So far, however, we have not yet observed any trace of superconductivity in the Q2D systems.
2. Basic properties of A2Cr3As3
As shown in Fig. 3(a), the A2Cr3As3 family is structurally characterized by the 
double-walled linear sub-nanotubes separated by the K+ counterions. Consistent with the Q1D crystal structure, the resistivity data [Fig. 3(b)] indeed show a strong anisotropy with an anisotropic ratio, 
, up to 120 at 50 K. The 
shows a quasi-linear behavior below ∼30 K, which may account for the large resistivity value and linearity in polycrystalline samples [Fig. 1(a)]. At around 50 K, interestingly, 
exhibits a resistivity maximum, characteristic of 3D-to-1D dimension crossover as observed in Q1D so-called Bechgaard slats.[28] This result suggests that a Tomonaga–Luttinger liquid (TLL) state could be realized at high temperatures.[28,29]
The inner Cr3 sub-nanotubes can be theoretically modelled in terms of a twisted Hubbard tube, which gives rise to 1D molecular-orbital bands.[31] Electronic band-structure calculations reveal that the electronic states near the Fermi energy are dominated by the Cr-3d atomic orbitals.[30] Note that the asymmetrical spin–orbit interactions are sizable around K and Γ points, as shown in the inset of Fig. 3(c). There are two Q1D Fermi-surface sheets (FSs) in the α and β bands and one three-dimensional (3D) FS pockets in the γ band [Fig. 3(d)].[30,32,33] The two hole-like Q1D FSs are experimentally observed in a recent angle-resolved photoemission spectroscopy study,[34] from which a TLL behavior is signatured. The TLL physics has been earlier suggested both experimentally[35] and theoretically.[31,36,37]
For the prototype compound K2Cr3As3, the total density of states (DOS) at EF is calculated to be 
,[30] corresponding to a ‘bare’ electronic specific-heat coefficient of 
. The experimental Sommerfeld coefficient (
) is 3.5 times larger,[10] indicating remarkable electron-mass renormalization (electron–phonon coupling constant is generally less than 1.0 owing to the lattice instability). Similar comparison between calculations and experiments for Rb2Cr3As3 and Cs2Cr3As3[32,33] suggests that the electron-mass renormalization factor decreases significantly with the interchain distance. Furthermore, there is a positive correlation between Tc and the Sommerfeld coefficient 
(Fig. 2). What controls the electron correlations? How do the electron correlations determine Tc as well as the superconducting pairing? What is the role of one dimensionality on superconductivity? These questions remains open at present.
Remarkably, the Cr-based Q1D arsenides show evidence of unconventional superconductivity with a possible spin-triplet pairing. Theoretical investigations based on an effective theoretical model[38–41] show that the most attractive pairing interactions are always in spin-triplet channels. Spin-triplet superconductivity is also suggested by the theoretical analyses in terms of the multiband TLL scenario[31,36] and melting of macroscopic spin polarization in a weakly coupled odd-gon-unit system.[42] Nevertheless, spin-singlet pairing with a 
-like gap function is obtained from a phenomenological two-band model.[37] Note that conventional electron-phonon mediated superconductivity is also proposed for K2Cr3As3.[43] The calculated total electron-phonon coupling constant is as large as 
, which seems too high to maintain the lattice.
Experimentally, the 75As Knight shift data[44] indicate the existence of ferromagnetic spin fluctuations, in favor of spin-triplet pairing, consistent with the theoretical calculations and analyses.[30,32] Additionally, the zero-field 
SR measurements show evidence of the spontaneous appearance of an internal magnetic field below Tc.[45] The NMR investigations show no Hebel–Slichter coherence peak,[35,44,46] against conventional superconductivity. Furthermore, the Cr-spin fluctuations are captured from the nuclear spin-lattice relaxation rate 1/
, implying non-phonon-mediated superconductivity. It was found that, with increasing the interchain distance, the strength of Cr spin fluctuations is progressively suppressed, together with the decrease in Tc.[46] The inelastic neutron scattering in K2Cr3As3 also indicates the existence of short-range magnetic fluctuations, which suggests proximity to a magnetic instability.[47] The incipient magnetic order is considered to couple strongly to the lattice and competes with superconductivity as well. As for the properties of the superconducting gap function, most experiments (including NMR,[35] 
SR,[45,48] penetration depth,[49,50] and specific heat[51]) mostly suggest the existence of line nodes, again favoring unconventional superconductivity.
The upper critical field (
) of A2Cr3As3 appears to be very unusual,[14] which also gives valuable information on the superconducting pairing. Nevertheless, there were very different interpretations to the experimental data.[17,52–54] To clarify the related issues clearly, in this paper, we present some basic knowledge first, then focus on the details of temperature and angular dependence of 
, and finally try to discuss the result on an equal footing.
3.
versus pair breakingTo understand the electron pairing in a superconductor, an alternative method is to investigate how the pairs are broken. The upper critical magnetic field 
of a type-II superconductor may serve as an indicator for unconventional superconductivity.[3] In the following, we first address how Cooper pairs are broken in a type-II superconductor if an external magnetic field is applied. Then, we present the general experimental method for the measurements of 
. We will focus on the 
data as functions of temperature and field direction in the A2Cr3As3 superconductors. The implication on the possible superconducting pairing symmetry is discussed. Note that this article has some overlap with our recent publications.[14,53,54]
As is known, superconductors can be classified into type-I and type-II superconductors, according to their responses to external magnetic fields. Unlike type-I superconductors, which show full diamagnetism (Meissner effect) until the external field exceeds the thermodynamic critical field 
, type-II superconductors are characterized by an additional phase, the mixed state (or vortex state), which contains quantized magnetic fluxons. The two phase boundaries (Meissner to mixed state and mixed state to normal state) define lower and upper critical fields, namely, 
and 
. According to Ginzburg–Landau (GL) theory, the borderline of type-I and type-II superconductors locates at 
, where κ is the so-called GL parameter, λ and ξ denote magnetic penetration depth and superconducting coherence length, respectively. In the case of orbital pair breaking, 
relates to ξ by the formula 
.
In general, a magnetic field suppresses superconductivity through the following two mechanisms. The first is the orbital pair breaking due to electromagnetic interactions, which is described by GL equations.[57] The purely orbital pair breaking limits the 
in a way characterized by a linear relation at 
, as shown in Fig. 4(a). The second is the so-called paramagnetic effect,[58,59] which is due to the difference in spin susceptibility between superconducting and normal states (the spin susceptibility of a spin-singlet superconductor is zero). If there were no orbital effects, then the spin paramagnetic effect by itself would yield 
(here the electron g factor is given to be 2.0), where Δ is the superconducting energy gap. Given the BCS result with 
, one obtains the so-called Pauli-paramagnetic (or Clogston–Chandrasekhar) limit, 
(in unit Tesla).[58,59] Note that paramagnetic pair breaking is featured by a concave-down curvature, as shown in Fig. 2(b), and 
holds near Tc. Since 
grows much faster than 
with decreasing T, therefore, an orbital pair breaking mostly dominates at 
.
The Pauli-paramagnetic limit can be exceeded either by strong coupling or by spin–orbit scattering. The latter effect can be parameterized by the Werthammer–Helfand–Hohenberg (WHH) theory,[55] which simultaneously includes both pair-breaking effects together with spin–orbit scattering [Fig. 4(c)]. It is found that spin–orbit scattering counteracts the paramagnetic effect in limiting 
. As a result, the 
can be significantly enhanced through spin–orbit scattering. Note that, in certain circumstances, a novel Fulde–Ferrel–Larkin–Ovchinnikov (FFLO) state with spatial modulations of superconducting order parameter may appear at high fields. The appearance of FFLO often accompanies an upturn in 
.[60,61]
In fact, the pair-breaking effect displayed in Fig. 4 only applies for simple isotropic, s-wave gap, and single-band cases, without the considerations of strong coupling, electron-mass anisotropy, nodal gap, and multiband scenarios. In particular, if the Cooper pairs are in a spin-triplet configuration, which can also be spin-polarized by the external field, then no paramagnetic effect is expected at certain field directions. In a spin-triplet pairing, the superconducting order parameter is expressed using a so-called 
vector,[1] thus only a certain field direction may avoid the paramagnetic pair breaking. In contrast, orbital pair breaking by electromagnetic interactions always exists (with exceptions for an extremely large anisotropy) regardless of the spin structure of the superconducting Cooper pairs. We will come back to this point later.
4. Measurement of 
In general, 
is measured by the sharp superconducting transition in a physical quantity under external magnetic fields. The physical quantities can be resistivity, ac susceptibility, dc magnetization, and heat capacity, etc. Two experimental modes can be employed, namely, field-sweep at a fixed temperature and temperature-sweep at a fixed field, which give 
and 
, respectively. One should find a suitable technique for the 
measurement, compatible with the specific cases and experimental conditions.
Among the different techniques mentioned above, measurement of resistivity under magnetic fields is the most common one, since it is relatively easily operated and accessible. Figure 5 shows an example for the anisotropic 
measurement of Rb2Cr3As3 crystals. Note that different crystals had to be used for different field directions owing to the sample’s extreme sensitivity to moisture (tiny moisture may deteriorate the sample) and also the apparatus’ incapability to rotate the sample in situ. What we emphasize here is about the criterion of 
in T-sweep (or 
in H-sweep). 
can be regarded as the lowest field in which the first magnetic vortex is allowed to enter the sample’s interior. Therefore, the junction between superconducting and normal states should be the position of 
(or 
), if superconducting thermal fluctuations are not remarkable. That is why here we employ onset superconducting temperature for the determination of 
.
In this work we employed a pulsed magnetic field up to 60 T in Wuhan’s National High Magnetic Field Center for the 
measurement of K2Cr3As3 crystals. For the high-field measurement of Rb2Cr3As3, we also employed the Cell 1 Water-Cooling Magnet of the High Magnetic Field Laboratory of the Chinese Academy of Sciences, which generates the maximum magnetic field up to 38.5 T and allows the magneto-resistance measurement down to 0.3 K. Note that it is very important to avoid the sample’s deterioration and keep the electrodes on the sample effective during the measurement.
5. Temperature dependence of 
5.1. K2Cr3As3 and Na2Cr3As3
Figure 6 shows the magneto-resistivity measurement result for K2Cr3As3 polycrystals, which gives an initial 
slope of 
.[10] By using the WHH formula without spin–orbit coupling,[55] one obtains a zero-temperature upper critical field of 
, which is three times the Pauli-paramagnetic limit 
. Thus the Maki parameter,[56] 
, is above 4, suggesting either a dominant Pauli-limiting effect at low temperatures or a novel spin-triplet superconductivity. In the case of Na2Cr3As3, the 
value is estimated to be 54 T,[16] 3.4 times of its Pauli limit (16 T). The result contrasts with another Q1D superconductor Tl2Mo6Se6 with 
, whose 
values are merely 5.8 T and 0.47 T, respectively, for magnetic fields parallel and perpendicular to the c axis.[62] Nevertheless, a large 
beyond the Pauli limit is seen in Q1D Li0.9Mo6O17,[63] which is regarded as evidence of spin-triplet superconductivity.[64]
Recalling that Tc decreases monotonically with applying pressures, very interestingly, the 
of the pressurized sample of K2Cr3As3 decreases much faster than Tc itself.[19] The 
value decreases to below the Pauli limit at above 2 GPa. The estimated Maki parameter drops from 4 at ambient pressure to well below 1 at 
, indicating a crossover from Pauli-paramagnetic limitation to orbital limitation. If the high 
value at ambient pressure represents a sign of spin-triplet pairing, the pressure-induced suppression of 
may suggest a breakdown of the spin-triplet pairing channel upon applying pressures.
Kong, Bud’ko, and Canfield[17] first reported the anisotropic 
in K2Cr3As3 crystals. The initial 
slopes were measured to be −7 T/K and −12 T/K, respectively, for 
and 
. Meanwhile, the results obtained by Zuo et al.[53] are −4.2 T/K and −10.3 T/K, and those by Wang et al.[65] are −5 T/K and −16.1 T/K, respectively. Although these data look scattered, primarily because of the sample’s sensitivity and the difference in the temperature range of linear fitting, the result points to a relatively weak effective-mass anisotropy with 
near Tc. Nevertheless, the upper bound of the effective-mass anisotropy is consistent with the resistivity anisotropy value at 
.[14]
Owing to the expected high 
at low temperatures, measurements under high magnetic fields are necessary to reveal the whole 
behavior. Balakirev et al.[52] measured 
and 
for K2Cr3As3 at high magnetic fields up to 60 T, using a contactless technique based on a proximity detector oscillator. The results show a Pauli-limited behavior for 
, yet 
exhibits an orbitally limited behavior with no signs of paramagnetic pair breaking. Consequently, an anomalous reversal in 
appears at ∼4 K.
We independently conducted the anisotropic 
measurements for K2Cr3As3 crystals by direct magnetoresistance measurement for the first time. A standard four-probe technique was employed, and the sample was installed on a rotator that bears pulsed magnetic fields up to 60 T.[53] Figure 7(a) and 7(b) show the field dependence of the magnetoresistance with 
and 
, respectively. 
can be clearly identified by the junction points between superconducting and normal states, although no zero-resistance is achieved due to the sample’s extreme sensitivity to the environment. The obtained 
data, plotted in Fig. 7(c), basically agree with those of the previous report.[52] Indeed, 
shows a downward curvature, in contrast with the upward curvature for 
. One also sees that 
and 
cross at 3.1 K. The low-temperature 
values for both field directions exceed the Pauli limit by a factor of 2–3. We will discuss the origin and its implications later on.
5.2. Rb2Cr3As3 and Cs2Cr3As3
The anisotropic 
measurement for Rb2Cr3As3 under relatively low fields is shown in Fig. 5, from which the 
data can be directly obtained. As is seen, the superconducting transition moves to lower temperatures with applying magnetic fields, and Tc is suppressed more rapidly for 
. The resultant 
data are plotted in Fig. 5(c). One sees that 
exhibits a steeper increase with decreasing temperature, but the magnitude of the slope tends to decrease. By contrast, 
increases slowly near Tc, yet the magnitude of the slope increases with decreasing temperature. The result in Cs2Cr3As3 shown in Fig. 8 is quite similar, although the 
values are close to the Pauli limit. Therefore, the contrasting 
and 
behavior is universal to all three members of A2Cr3As3. As illustrated in Fig. 4, the concave-down feature in 
indicates a dominant Pauli-limited pair-breaking mechanism. The almost linear 
characteristic meets an orbitally limiting mechanism. The slight concave-up behavior may reflect multiband superconductivity since there are three or four FSs in the system.[32,33]
Generally, orbital pair breaking dominates 
at 
. This means that the initial slope of 
is a measure of the orbitally-limited upper critical field at zero temperature, 
. From the data in Fig. 5(c), we obtain the initial slopes of 
and 
, respectively, for Rb2Cr3As3. The data of Cs2Cr3As3 (in Fig. 8) show 
and 
. According to GL theory, the effective-mass anisotropy, 
, are about 30 and 50, respectively, for Rb2Cr3As3 and Cs2Cr3As3. The result suggests stronger Q1D anisotropy in Rb2Cr3As3 and Cs2Cr3As3, consistent with the larger interchain distance in the crystal structure.[14]
Figure 9(a) and 9(b) show the field dependence of resistance at fixed temperatures with different field directions in Rb2Cr3As3. We employ the identical criterion for the determination of 
. While it is evident to determine the 
for sample C (with 
) which shows a single sharp superconducting transition, however, it turns out to be ambiguous for sample D (with 
) because it exhibits two main transitions (possibly arising from the electrode contact problem and/or sample’s partial deterioration.[20,21]). Figure 9(c) presents an additional data set for 
, from which we find the steepest transition to use for the 
determination. The resultant 
data are displayed in Fig. 9(d). One sees that different sets of data basically meet each other. The 
phase diagram looks similar to that of K2Cr3As3. Firstly, 
shows an obvious downward curvature, characteristic of Pauli-limiting behavior. 
tends to saturate to 17.5 T, twice of 
, without any sign of the formation of the FFLO state. The enhanced 
seems to be mostly related to the strong coupling superconductivity as evidenced by the large specific-heat jump 
.[10] Secondly, 
is approximately linear in the whole temperature range, which strongly suggests the absence of the Pauli-paramagnetic pair breaking effect. In particular, 
keeps increasing linearly down to 0.075Tc. This suggests that, apart from the orbitally pair-breaking effect with the typical 
profile shown in Fig. 4(a), there could be a positive role played by external magnetic fields for superconductivity. Spin-triplet with equal-spin pairing may account for such a novel 
behavior. Thirdly, the 
data for K2Cr3As3 and Rb2Cr3As3 almost coincide with each other, although the latter shows a larger anisotropy close to Tc. In both cases, the apparent 
reversal at about 0.4Tc actually reflects different pair breaking mechanisms for different field directions. We will further address this issue with the measurement of polar-angle dependence.
The phenomenon of 
reversal, i.e., crossing between 
and 
, has been witnessed in several other systems including the Q1D organic superconductor (TMTSF)2PF6,[66] iron-based chalcogenides,[61,67,68] and the heavy-fermion superconductor UPt3.[69] At first sight, the reversal in 
K2Cr3As3 and Rb2Cr3As3 suggests a dimension crossover. However, it seems unlikely from the crystal and electronic structure points of view. Moreover, the dimension crossover scenario can be ruled out by our 
data (see below) which show modulations at the “crossover” temperature of 3.1 K. This is definitely inconsistent with the expected angle dependence, 
, in which a constant 
is given for the effective-mass ratio 
.
We note that details of the 
behaviors differ in different systems. In (TMTSF)2PF6, 
shows a pronounced upward curvature for the field directions perpendicular to 
at low temperatures.[66] This arises from the dramatic reduction of the orbitally pair-breaking effect owing to a field-induced dimension crossover.[3] In iron-based superconductors, the 
data reveal that the Pauli-limiting effect is always at work regardless of the field directions,[61,67] consistent with a spin-singlet pairing. The anisotropy inversion appears only accidentally, and 
generally approaches 1.0 at 
,[70] which actually reflects the Pauli-paramagnetic pair breaking effect associated with anisotropic spin–orbit coupling. By contrast, the reversed anisotropy ratio in UPt3 is sizable at zero temperature,[69] similar to the case here in A2Cr3As3 (A = K and Rb). As for Cs2Cr3As3, although the Maki parameter decreases to 1.8 for 
, the 
data show a linear dependence, suggesting that there is still a possibility of an absence of the Pauli-limiting effect for 
.
6. Angle dependence of 
in K2Cr3As3
6.1. Polar-angle dependenceTo further clarify if there is any “residual” Pauli-limiting effect for 
, we performed the angle dependence measurement. Namely, the sample rotates in situ such that the field direction tilts a “polar” angle θ from the c axis, as shown in the inset of Fig. 10. First of all, at temperatures near 
, 
decreases monotonously with increasing θ (from 0° to 90°). This is understandable since there is a uniaxial effective-mass anisotropy. As the temperature is lowered, an additional maximum in 
appears at θ = 90°. The enhanced 
is consistent with the reduced Pauli-limiting effect for 
.
Below we show that the whole 
data set can be perfectly explained by the combination of a fully anisotropic Pauli-limiting effect (i.e., absence of Pauli-limiting effect for 
) with a uniaxial effective-mass anisotropy. According to GL theory, the effective-mass anisotropy leads to the anisotropy of the orbitally limited 
,
where
denotes the presumed orbitally limited upper critical field for
and,
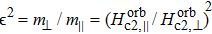
is the effective-mass ratio. Indeed, equation (
1) can basically describe the experimental
data at 5 K (albeit of obvious deviations at
). However, it completely fails to meet the
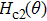
data at lower temperatures.
The reason for the failure of Eq. (1) is because the paramagnetic pair breaking effect is not included. Given the contrasting 
behavior for 
and 
, the paramagnetic pair breaking is assumed to be fully anisotropic. Namely, only the magnetic-field component parallel to the c axis further suppresses the 
in Eq. (1). The paramagnetically pair-breaking effect can be parameterized by an effective Pauli-limiting field 
. Therefore, we have 
, in which 
(fully Pauli limiting) for θ = 0° and, 
(absence of Pauli limiting) for θ = 90°.
The effective Pauli-limiting field 
suppresses 
in a way of competition between the related energies.[55,58,59,71] Given 
, therefore, 
. Consequently, one obtains an explicit expression for 
,
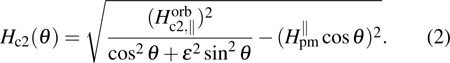
Remarkably, the whole experimental data set of 
satisfies the above equation very well, as shown in Fig. 10, which further clarifies the absence of the Pauli-limiting effect for 
. The data fitting yields three parameters, 
, ϵ, and 
at a given temperature. As expected, the fitted 
is basically linear. The linear extrapolation yields a zero-temperature orbitally limited 
of 51.5 T for 
, which is reasonably larger than the extrapolated value of 
for 
. The obtained 
and 
exceed the Pauli limit 
by a factor of 4.6 and 3.4, respectively. Using the GL relations, 
and 
, where 
is the flux quantum, the anisotropic coherence lengths at zero temperature can be estimated to be 
and 
. The 
value exceeds twice the interchain distance in K2 Cr3As3,[10] indicating the nature of anisotropic 3D superconductivity.
6.2. Azimuthal-angle dependenceFigure 11(a) shows derivative of the magnetoresistance for the field directions with different azimuthal ϕ angles. The 
data can be extracted by the peak value in dR/dH (here we use a different criterion so as to increase the measurement precision). The ϕ angle varied from 1.87° to 153.38°. According to the crystal symmetry with the point group of 
, the data set is rotated by 120° and −120°, respectively, in order to plot a complete polar diagram. One sees that the overlapped region matches well, which validates the rotation. Consequently, the obtained 
profile shows a three-fold modulation with an amplitude of 0.36 T. The maximum of 
appears for the field directions along the crystallographic a and b axes. Here the possibility of surface superconductivity and the influence of anisotropic normal-state magnetoresistance can be excluded (see the Supplementary Materials in Ref. [53]). Note that the 
modulation (with a relative magnitude up to ∼1.2%) in K2Cr3As3 is actually more obvious than those in UPt3[72] and MgB2,[73] both of which also crystallize in a hexagonal lattice.
The sixfold modulation of 
in UPt3[72] can be explained in terms of a coupling to the symmetry breaking field.[74] In the case of K2Cr3As3, according to the first-principles calculations, the magnetic ground state appears to be a novel in-out co-planar magnetic order,[30,32] as shown at the lower-right corner in Fig. 11(b). The magnetic moments lie in the basal plane. Intuitively, this result seems to be compatible with the observed 
modulation that can be similarly explained by the coupling to the symmetry breaking field.
7. Discussion and conclusionFor a conventional superconductor with a high 
comparable to 
, the 
value is normally limited by the paramagnetic effect regardless of field directions. Considering the paramagnetically limited behavior of 
in K2Cr3As3, as well as the preliminary observation of the insensitivity of Tc on impurity scattering, Balakirev et al.[52] proposed a novel spin-singlet superconductivity. The absence of the Pauli-limiting effect for 
is explained by assuming electron-spin locking along the c direction. In fact, we have demonstrated that the apparent insensitivity of Tc on impurity scattering is due to the clean limit (
) for the superconductivity (see below). So, their staring point seems to have deviated. Secondly, according to the first-principles calculations,[30,32] the Cr moments likely align perpendicular to the chain direction that is possibly associated with the sizable spin–orbit coupling shown in Fig. 3(c), contradicting with the Ising-like spin-locking scenario. More importantly, our in-plane 
profile also opposes the Ising-like spin-singlet superconductivity.
We argue that spin-triplet pairing explains the overall 
data more naturally. The absence of the Pauli-limiting effect for 
and a large 
value (3.4 times of 
) actually dictate a spin-triplet pairing scenario, as in the case of UPt3.[4] The latter was recently confirmed to host a spin-triplet odd-parity superconductivity.[75] The (pseudo)spins of the odd-parity Cooper pairs are 
with 
, which is equivalent to the spin state of 
. In this circumstance, the Zeeman energy breaks the Cooper pairs for 
, hence the Pauli-limiting behavior for 
. By contrast, the perpendicular field simply changes the population of Cooper pairs with spin directions 
and 
, and therefore, no paramagnetic pair-breaking is expected for 
. Indeed, by taking spin-triplet pairing into consideration, and with some simplifications and approximations, we are able to derive an equation for 
, whose solution is consistent with Eq. (2) (for details see the Supplementary Materials in Ref. [53]). Here we note that, owing to the non-centrosymmetric crystal structure in K2Cr3As3, the pairing symmetry is in principle a mixture of singlet and triplet states,[38] except for the case of a simple pz wave in which a purely triplet pairing is anticipated because of the mirror-plane reflection symmetry.[39]
Finally, we comment on the impurity scattering effect on Tc, which is important to judge the possibility of either the singlet or triplet pairing state. For an odd-parity unconventional superconductor, nonmagnetic scattering serves as a source of pair breaking even at zero field, hence Tc suppression is expected. However, such an impurity scattering effect will not be evident in the clean-limit regime, i.e., the electron mean free path l is much larger than the superconducting coherence length ξ. In K2Cr3As3, l is estimated to be ∼75 nm (after the electron-mass renormalization is considered) for the electron transport along the c axis in the sample with RRR = 61, and 
is only 3.5 nm, thus 
holds. A similar case is seen in Rb2Cr3As3.[54] This explains why the Tc keeps almost unchanged for single-crystal samples with different RRRs. Our recent study shows that, when introducing sufficient impurities (
), Tc is indeed suppressed in K2Cr3As3.[15]
In conclusion, we show that the detailed 
measurements supply very important information on the superconducting pairing of the Q1D Cr-based superconductors. The apparent “anisotropy-reversal” phenomenon actually reflects different pair-breaking mechanisms for different magnetic-field directions. The absence of paramagnetic pair breaking for 
is further clarified by the 
data set in K2Cr3As3. The three-fold modulation in 
implies time-reversal symmetry breaking in the superconducting state. The spin structure of the superconducting Cooper pairs probably involves Cr-spin locking within the ab plane, and the dominant pairing is likely to be of a spin-triplet state, which seems more natural to explain the full 
data. So far, the spin-triplet pairing scenario is consistent with the previous suggestions in experimental and theoretical investigations. Nevertheless, clarification of the specific pairing symmetry needs more investigations.
Unconventional superconductivity has been and remains one of the major topics in the area of condensed matter physics. According to the classification by Hirsch, Maple, and Marsiglio,[76] there are 11 classes of materials that can be categorized into “unconventional superconductors” in which superconductivity does not come from conventional electron-phonon interactions. The present status of the research, in particular, with the 
measurement, strongly suggests that the newly discovered A2Cr3As3 superconductors should belong to the unconventional category.
Acknowledgment
We thank Pi L, Xi C Y, Bao J K, Tang Z T, Liu Y, Zuo H K, Wang J H, Kang J, Xu Z A, Yuan H Q, Cao C, Ning F L, Imai T, Zheng G Q, and Sun L L for our fruitful collaborations. Thanks are also due to Agterberg D F, Zhang F C, Zhou Y, Dai J H, Luo J L, Cheng J G, Yang F, and Hu J P for their helpful discussions.
