† Corresponding author. E-mail:
In this paper, a new evolutionary algorithm, the well-known imperialist competition algorithm, is proposed for optimizing the optical thin-films. In this method, the process is modeled of the competition between countries as imperialists and their colonizing of others as colonies. This algorithm could be an appropriate alternative to some of the more popular algorithms for optimizing the optical thin-films for good performance. The polarizer and edge filter for example are designed by using the imperialist competition algorithm method and the results are compared with those from two optimization high-performance methods: the genetic algorithm and differential evolutionary algorithm. Based on these results, the performance of the imperialist competition algorithm method shows that this algorithm is not sensitive to the change of its parameters and it can be an important advantage for quickly achieving a global optimal point. On the other hand the results show a better ratio of P-polarization transmittance to S-polarization transmittance in the design of a 1540-nm polarizer, which is more appropriate than the results from the other two methods. In the second design, an edge filter with a lower number of layers and more uniform bandpass spectrum than the counterparts of those methods is obtained. These results indicate that the imperialist competition algorithm is a robust method for optical thin-film designs.
Optical thin-films today have many applications in various high-tech areas such as lasers, simulation technology, guidance technology, and so on. One of the main concerns in designing a filter is to develop a method of creating a filter with the best performance and the lowest number of layers and thickness.[1] Different methods of this design are divided into three general categories: analytical, graphical, and numerical methods.[2–4]
Numerical methods include refinement methods and synthesis methods. In designing filters, the starting point is an important issue that should be considered in the use of refinement methods, but in synthesis methods, by creating a preliminary filter design, optimization steps can be done. Synthesis methods such as the evolutionary algorithm and needle method[5–7] are much less sensitive to the point and can evolve the design for suitable results automatically.
In this paper, we propose an evolutionary algorithm as a new method of designing optical thin films. First, we explain how this algorithm works, then how it is adapted to the optimization problem of a filter, and finally, we compare its results with those from other methods. To illustrate the ability of the algorithm to optimize the filters, we consider two high-performance examples and optimize them by two efficient and powerful algorithms, the genetic algorithm (GA) and differential evolution (DE), which are used to optimize optical thin films with various applications,[8–11] and then we compare the results with those from the new algorithm. The results obtained from optimization of the polarizer at the wavelength of 1540 nm by the new method indicate a thin-film design with a higher ratio of P-polarization transmittance to S-polarization transmittance (Tp/Ts) than other methods. This polarizer is used in a laser system to obtain linear polarization for the Q switching process. On the other hand, in the second example, the results obtained in the new method represent a plan with fewer layers and less thickness.
The imperialist competitive algorithm (ICA) is a type of evolutionary algorithm. It is a synthesis optimization method inspired by political, social, and cultural competitions between countries. For more theoretical details, see Ref. [12].
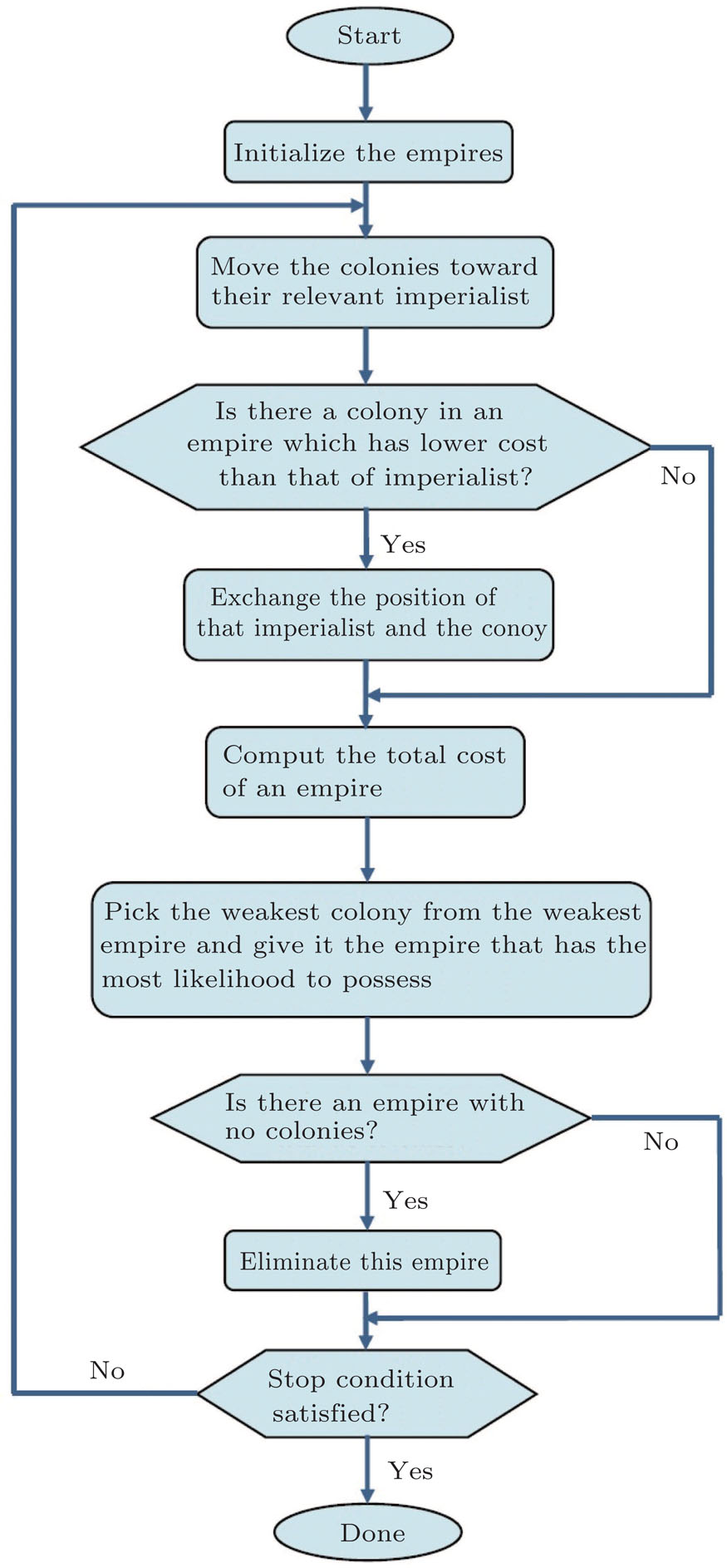
Like other evolutionary algorithms, the ICA algorithm begins with a random primitive population and each member of it is a country with Nvar number of decision variables. Here pi’s are decision variables of the country, which could be some characteristics of it such as politics, culture, and so on.
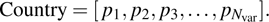
Some of the best members of the population are chosen as imperialists and others as colonies.
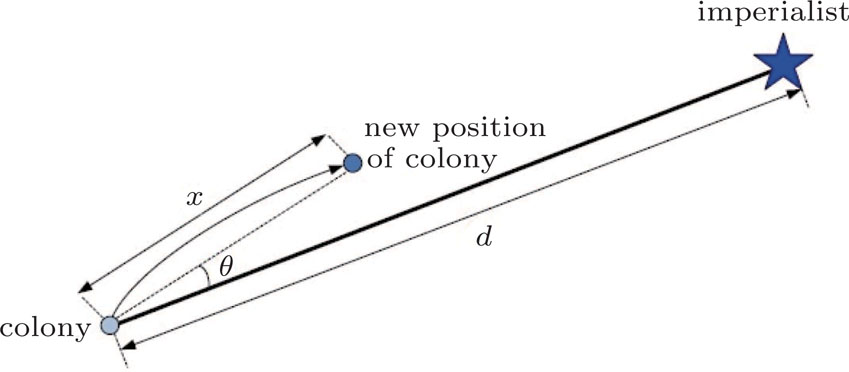
Assimilation of the colonies is done in order to approach the character of their imperialists.
According to Fig.


In the process of moving colonies to imperialists it is possible that some of the colonies achieve a better cost function than their imperialist; in this case, the colony and imperialist are replaced and the algorithm continues with the new imperialist.
The cost of empire is equal to the cost of the imperialist country plus a percentage of the total cost of its colonies and is expressed as




In this part, we investigate, for example, two multilayer filters using ICA, genetic algorithm, and differential evolution, and compared their results. To match the algorithm with the optimization process, each country with its total characteristics corresponds to a filter with its thickness of layers. Each characteristic of a country (pi’s) such as politics, culture, economy, etc., corresponds to the thickness of a layer of filter.
Several parameters such as thickness, materials, and number of layers are important for designing these examples. On the other hand, founding the global optimal point by selecting appropriate effective parameters of the algorithm is important. To design such filters, two materials with the highest difference between their refractive indices are required. Therefore, we consider a material with a low refractive index SiO2, which has a high laser-induced damage threshold against laser radiation for high refractive index material TiO2 was selected. It has transparent layers in the visible and near infrared region and also has a high laser-induced damage threshold.[13–16] These multilayer filters consist of several pairs of layers with high and low refractive index materials, which are TiO2 and SiO2 with refractive indices nH = 2.25 and nL = 1.46 respectively which are deposited on BK7 (ns = 1.51) substrate. Design is carried out by MATLAB software.
The merit function is one of the important elements in optimizing the thin-film filters. The main goal is to minimize the merit function to achieve a more satisfactory result, which is obtained by changing the layer thickness.[17,18] The merit function is the root-mean-square error between the calculated transmittance and the target value of transmittance in each iteration. A suitable merit function is defined as


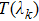




The first example is a Brewster polarizer[19] at a wavelength of 1540 nm, which was designed and optimized by using the ICA method. The incident ray angle is the Brewster angle of the BK7 substrate (56°). The selection of the Brewster angle as the incident angle reduces the reflection of P-polarization and improves the performance of the polarizer.[20–22]
Our target is designed to have high P-polarization (Tp and low S-polarization (Ts) for transmittance lightwave at 1540-nm wavelength. On the other hand, our main effort is to achieve a greater value for the Tp/Ts ratio in optimizing this polarizer. The initial number of layers was chosen to be 20 and the thickness of layers was selected to be in a range from 10 nm to 300 nm. According to Ref. [23], a thin layer less than 10 nm does not have much effect on the quality of target approximation. Table
| Table 1.
Some differences among results obtained by changing algorithm parameters. . |
| Table 2.
Characteristics of optimized polarizers. . |
According to Table
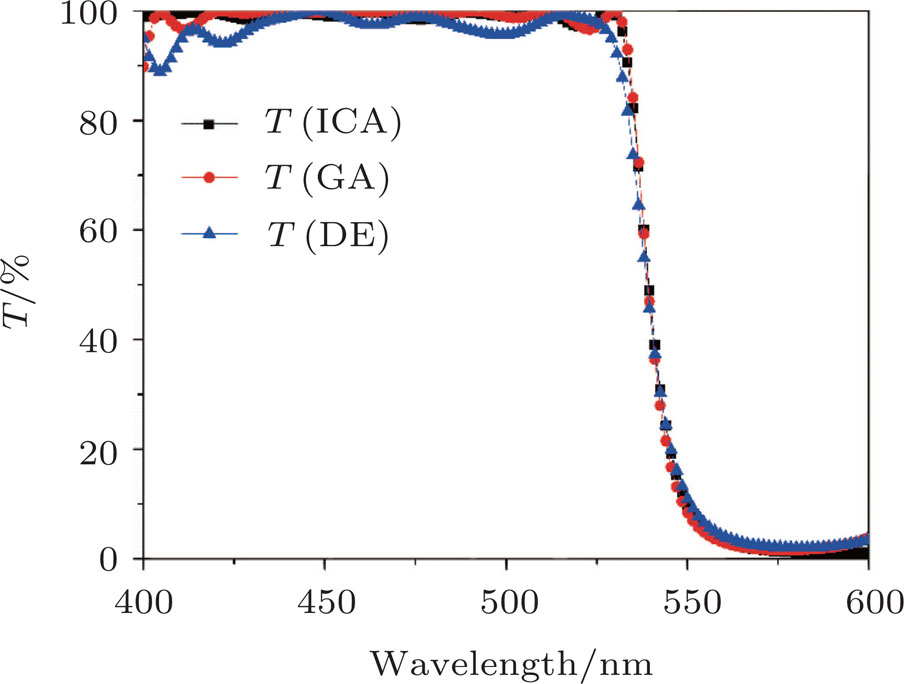
The second example is an edge filter in the visible range. It is also composed of two materials TiO2 and SiO2 on BK7 substrate. Our target has a high transmittance value between 400 nm and 550 nm but a low transmittance value between 550 nm and 700 nm. Table
| Table 3.
Characteristics of optimized edge filters. . |
Figure
The ICA method of optimizing the optical thin-films is proposed. Using the ICA method, a polarization with a high Tp/Ts ratio at the desired wavelength can be obtained. In addition, an edge filter with a wide passband, close to 100%, a wide stopband, and fewer layers is available from this method. As examples indicate, the design of a polarizer and an edge filter shows that the ICA method is a very robust method. Also, due to the low sensitivity of this algorithm to the change of its parameters, it will be easier to reach a global optimal point than by other algorithms. So this evolutionary algorithm could be a suitable alternative for some algorithms such as GA and DE in the optimization of optical thin-film filters.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |