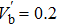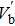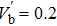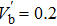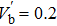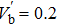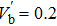† Corresponding author. E-mail:
The propagation characteristics of nonlinear ion–acoustic (IA) solitary waves (SWs) are studied in thermal electron–positron–ion plasma considering the effect of relativistic positron beam. Starting from a set of fluid equations and using the reductive perturbation technique, we derive a Korteweg–de Vries (KdV) equation which governs the evolution of weakly nonlinear IA SWs in relativistic beam driven plasmas. The properties of the IA soliton are studied, and it is shown that the presence of relativistic positron beam significantly modifies the characteristics of IA solitons.
The nonlinear propagation of solitary waves and shocks (SWS) in multicomponent plasmas has been widely studied for understanding the electrostatic disturbances in various plasma environments.[1–5] The study of electron–positron–ion (EPI) plasmas has been growing extensively due to their presence in the early universe, in the active galactic nuclei, in the pulsar magnetosphere, ionosphere, in the solar atmospheres, etc.[6–11] It is well known that when positrons are introduced into an electron–ion plasma, the response of the electrostatic waves changes significantly in comparison to the usual two component plasmas.[5,12,13] Therefore, it is worthwhile to study the nonlinear wave propagation in electron–positron–ion plasmas for understanding the dynamical behaviour of astrophysical and laboratory plasmas.[14–20] In the latter, the authors have shown that the nonlinear waves in the plasmas having positrons behave differently. Misra et al.[5] reported that the nonlinear mode of propagation and interaction in an electron–positron plasma exhibits a remarkable feature which is quite distinctive from the linear mode. Also, in some earlier works, Popel et al.[14] have found that the maximum amplitude of ion–acoustic (IA) solitons could be considerably reduced when a substantial fraction of hot positrons was present in the system. Interestingly, in a plasma system when a source of beam is inserted, it makes the system prone to a well-known streaming instability. Recently, Shan et al.[20] showed that due to the increased speed of positron beam and super-thermal electrons, the region of existence, amplitude, and width of solitons can be modified. Again, very recently, Shan et al.[21] found that with the variation in positron beam speed and positron population, and nonlinearities of the plasma system can be predominantly changed. Therefore, the options to create intense sources of positrons capable of fuelling extensive antimatter related research need to be developed, and this gap or requirement motivated us to start our investigation on ion–acoustic solitary waves (IASWs) in EPI plasmas with a relativistic positron beam impact which is a new kind of study not reported elsewhere as far as our knowledge is concerned.
Some of the earlier works considered electron-ion and EPI plasmas, however, most of them were non relativistic in nature.[3,22] But when the particle velocities are comparable to the speed of light, relativistic effects should be taken into account. Many researchers in due course of time exhibited the importance of relativistic effects in the modification of plasma wave dynamics.[23–29] In the ionospheric plasma system,[30] there is always a possibility of its interaction with highly intense charged particle beam coming from outer space. Therefore, in such conditions, the solitary wave in nonrelativistic plasmas may interact with relativistic charged particle beam. Based on all such observations, our brief communication has heralded on a model of EPI plasma to know the various effects of relativistic positron beam on soliton dynamics.
In the present paper, we investigate the propagation characteristics of ion–acoustic solitons in a relativistic beam driven plasma, and employ a new potent mathematical formalism known as the homogeneous balance method probably first generated by Wang et al. to show the solution of a Korteweg–de Vries (KdV) equation.[32] Here, Wang et al. introduced a new direct method called the homogeneous balance method to look for travelling wave solutions of nonlinear evolution equations with variable coefficients. It is seen that the method presents a wider applicability for handling many kinds of nonlinear evolution equations, such as high-dimensional equations, variable-coefficient equations, and differential-difference equations. The method is based on the homogeneous balance principle and linear ordinary differential equation (LODE) theory. Being concise and straightforward, this method has been applied to handle nonlinear partial differential equations in a direct manner with no requirement for initial/boundary conditions or initial trial function at the outset.
This paper is structured as follows. Section
We consider the nonlinear propagation of IASWs in an unmagnetized plasma consisting of thermal electrons and ions with a flow of relativistic positron beam. The basic equations governing the plasma dynamics can be written as

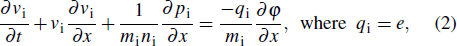
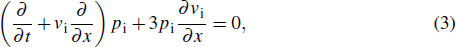

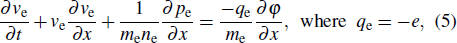
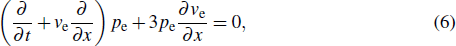

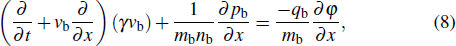
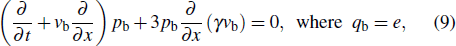
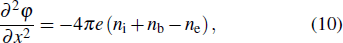
The collective effects in electron–positron plasmas can be studied if the electron–positron time scale is much longer than the electron–positron plasma effects, which is typically inverse of the plasma frequency. In a relativistic regime, the processes of creation and annihilation of electron–positron pairs become important. Before studying the nonlinear properties of the electron–positron plasma, it is necessary to take a look at the electron–positron pair annihilation time. Based on the theory of Svensson[32] concerning the electron-positron pair equilibria in relativistic plasma, to neglect the annihilation effect, the following inequality must be satisfied:


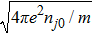
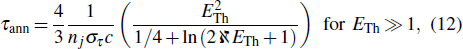
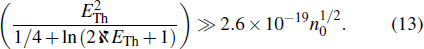
Now, we normalize the physical quantities as follows: T = tωpi, X = xωpi/cs, Vj = vj/cs, Nj = nj/nj0, Φ = eφ/kBTe, Pj = pj/nj0kBTj, where 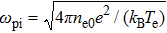
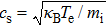

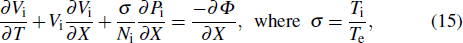
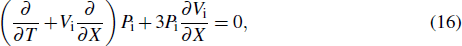

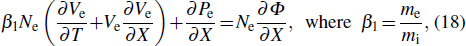
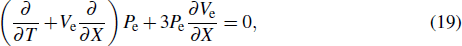

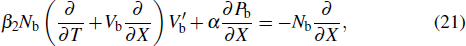
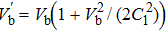
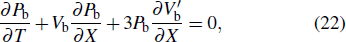
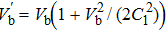
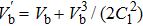
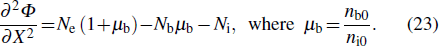
In order to derive the evolution equation for the propagation of IASWs in a relativistic positron beam plasma, we use the reductive perturbation technique in which the independent variables are stretched as λζ = ε1/2(X − T), τ = ε3/2T, where λ is the phase velocity and ε is a small nonzero constant measuring the weakness of the dispersion.
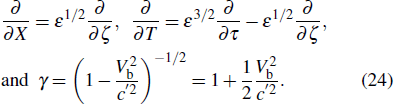
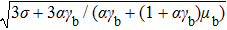
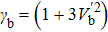
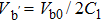
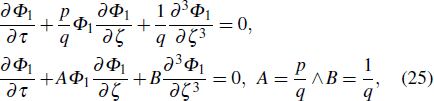
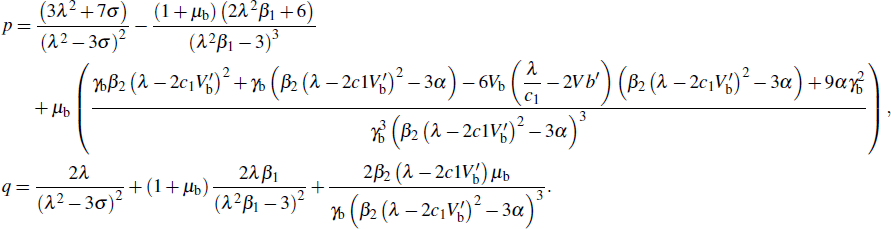
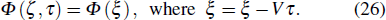
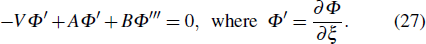
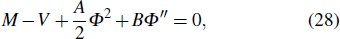
In order to get the soliton solution of Eq. (
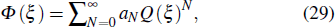
Now substituting the value of Eq. (
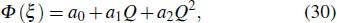
Here Q(ξ) = 1/(1 ∓ eξ) satisfies the following equation
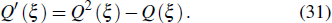
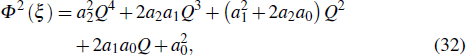

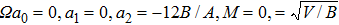
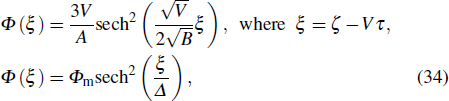
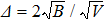
In what follows, we study the effects of the relativistic positron beam and other plasma parameters on the profiles of IASWs. The effects of nonlinearity become significant when the amplitude of the wave is sufficiently large. Nonlinear structures such as solitons and shocks are formed due to relative competition between nonlinearity, dispersion, and dissipation. When the effect of dissipation is small compared to nonlinearity and dispersion, the system can be supportive for the formation of solitons. The existence of a soliton solution with finite amplitude (Eq. (
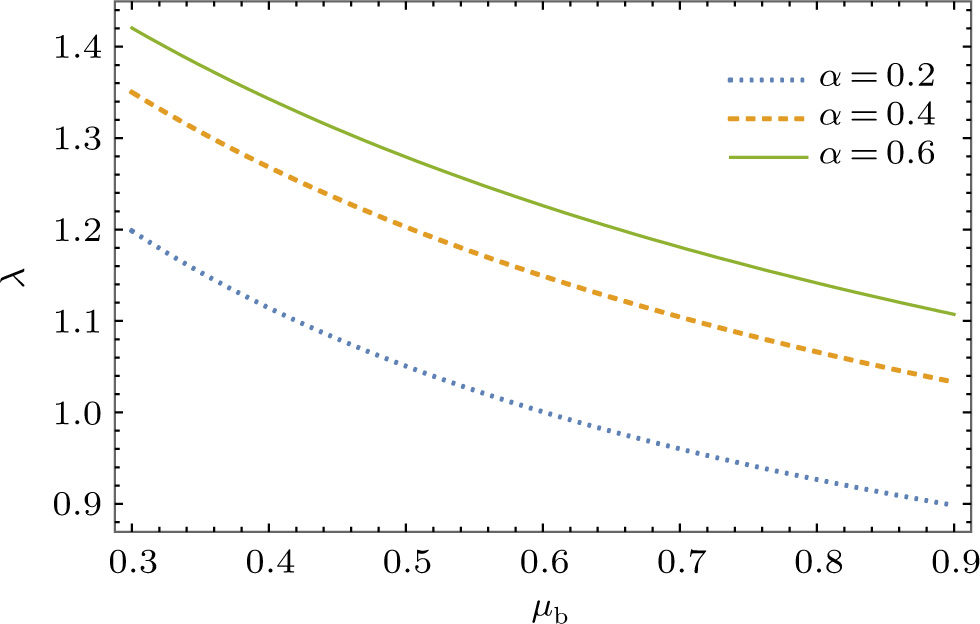
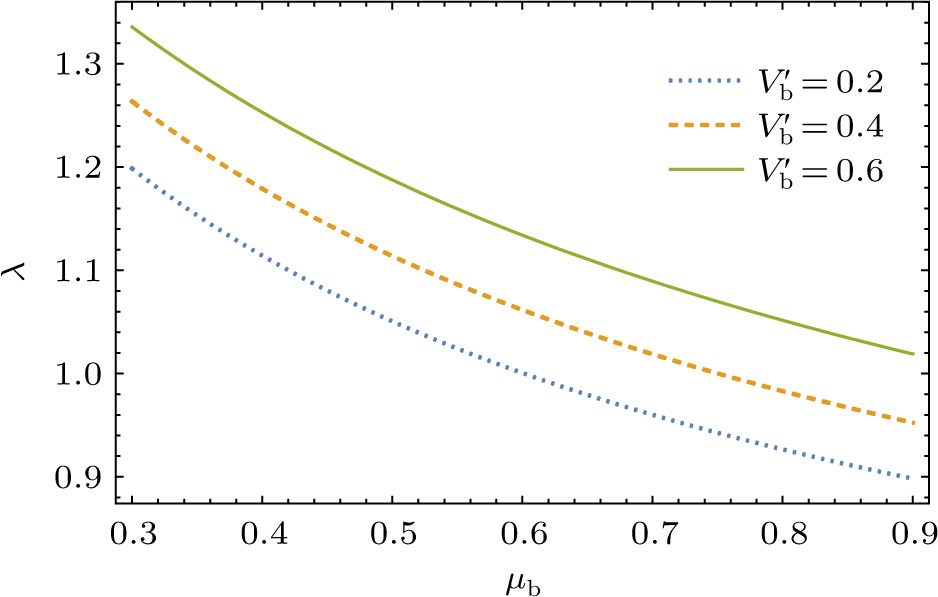
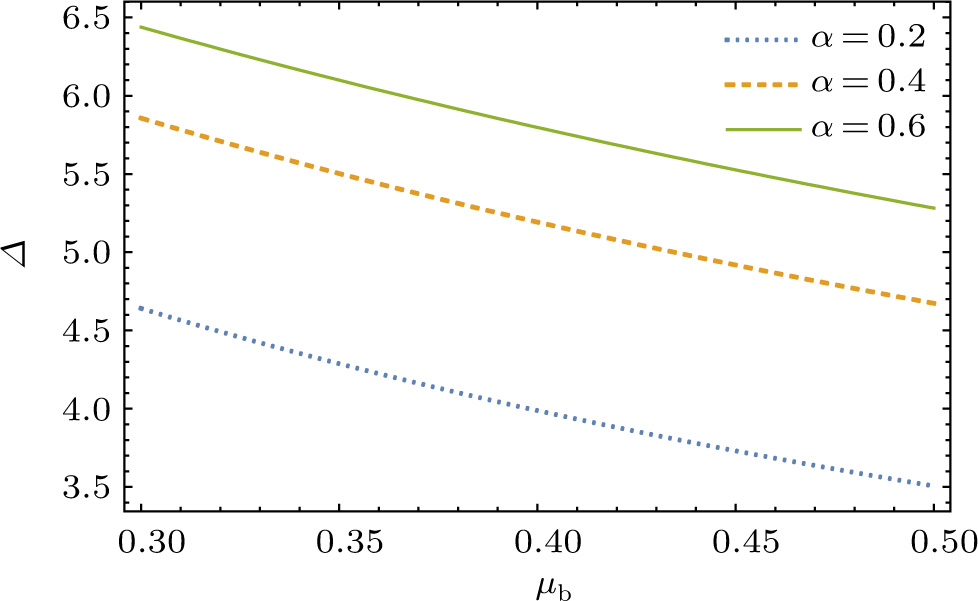
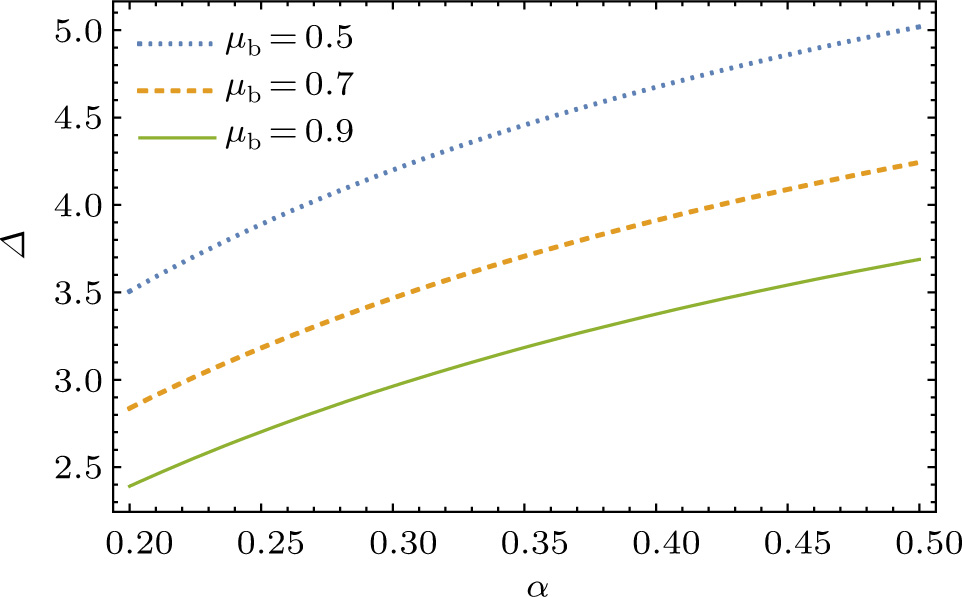
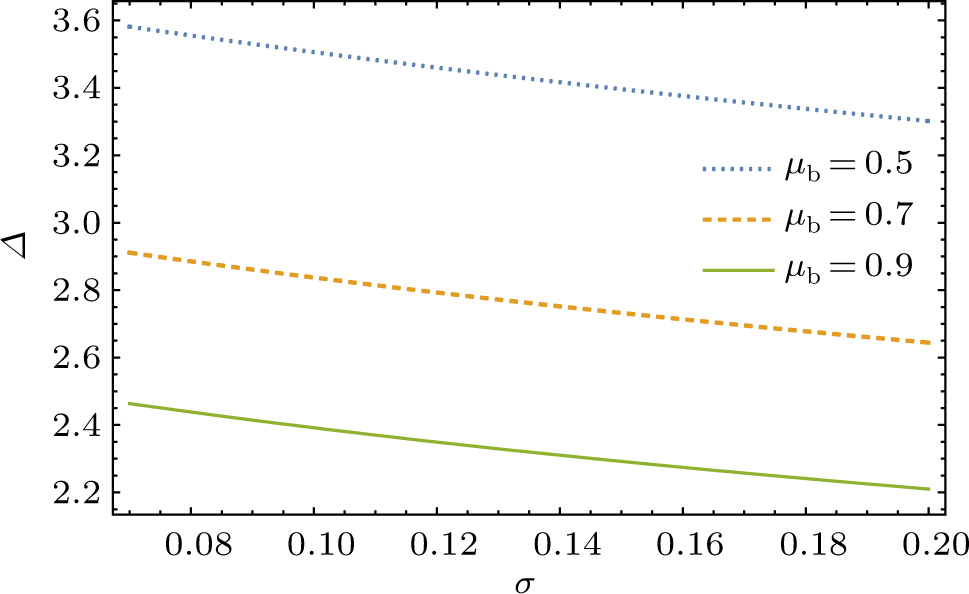
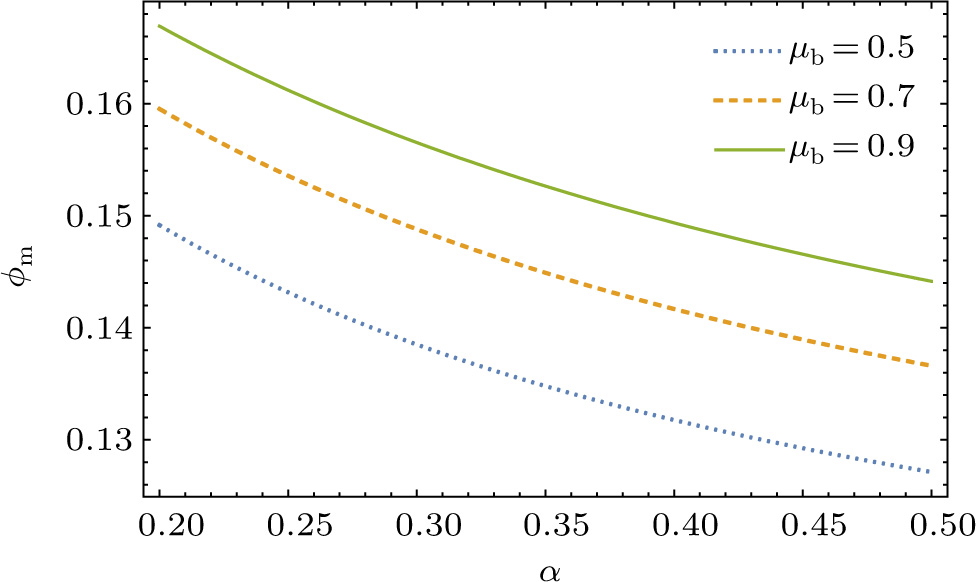
We numerically examine in Fig. 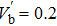
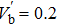
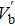
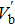
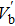
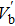
Next, we examine the properties of the soliton solution, namely its amplitude and width for different values of the system parameters. The results are shown in Figs. 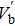
We have investigated the propagation characteristics of ion–acoustic solitary waves in an unmagnetized thermal electron–ion plasma with a flow of relativistic positron beam. Using the reductive perturbation technique, the KdV equation is derived which governs the evolution of weakly nonlinear ion–acoustic solitons in relativistic beam driven plasmas. The effects of the plasma parameters, namely the ion to electron temperature ratio, the beam to electron temperature ratio, and the relativistic parameter due to the flow of positron beam on the profiles of the ion–acoustic solitons, are studied. It is found that the propagation characteristics of ion–acoustic solitons are significantly modified by these plasma parameters. To conclude, the results should be useful for understanding the properties of ion–acoustic solitons that may be relevant in laboratory and space plasmas.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |