† Corresponding author. E-mail:
Project supported by the “Strategic Priority Research Program” of the Chinese Academy of Sciences (Grant No. XDA01020304), the National Natural Science Foundation of China (Grant Nos. 11747306 and 11565022), and the Youth Science and Technology Foundation of Gansu Province, China (Grant No. 1606RJYA263).
The small amplitude dust ion-acoustic double layers in a collisionless four-component unmagnetized dusty plasma system containing nonextensive electrons, inertial negative ions, Maxwellian positive ions, and negatively charged static dust grains are investigated theoretically. Using the pseudo-potential approach and reductive perturbation method, an energy integral equation for the system has been derived and its solution in the form of double layers is obtained. The results appear that the existence regime of the double layer is very sensitive to the plasma parameters, e.g., electron nonextensivity, negative-to-positive ion number density ratio etc. It has been observed that for the selected set of parameters, the system supports rarefactive, (compressive) double layers depending upon the degree of nonextensivity of electrons.
The field of dusty plasma physics has become a hot point of interest in recent years, due to its wide application in space and laboratory dusty plasma environments.[1–5] Many phenomena and mechanism of the processes are relevant to the knowledge of plasma wave in studying of the dusty plasmas, such as the plasma parameters measurement,[6] diagnosis,[7] wave heating,[8] and communication,[9] etc. There are different types of acoustic modes propagating in dusty plasmas depending on their time scales.[10–13] One of these waves is the dust ion-acoustic double layers (DLs), which is a nonlinear structure consisting of two oppositely charged parallel layers.
In the past few years, the ion-acoustic DL has been a topic of significant interest because of its relevance in cosmic applications,[14–17] confinement of plasma in tandem mirror devices,[18] ion heating in linear turbulence heating devices,[19] etc. Using the pseudo-potential approach and reductive perturbation method, several authors[20–23] have studied ion-acoustic DLs in different plasma systems. Electronegative plasmas, i.e., plasmas containing an appreciable amount of negative ions, are found in plasma processing reactors,[24] neutral beam sources,[25] the cometary comae,[26] and the upper region of Titan’s,[27] etc. Therefore, the importance of negative ion plasmas to the field of plasma physics is growing day by day. Ghebache and Tribeche[28] investigated small amplitude DLs in an electronegative plasma with nonextensive electrons. It has been observed that the ion-acoustic wave phase velocity, in different concentration of negative and positive ions, decreases as the non-extensive parameter q increases. Shaukat and Nadia[29] investigated small amplitude DLs in a warm electronegative plasma with trapped kappa distributed electrons. They have found that the small amplitude ion-acoustic DLs are significantly modified by the variation of various parameters such as the electron trapping efficiency and the ratio of the mass of negative ion to positive ion.
It is well known that the Maxwell distribution is taken to be valid for the macroscopic ergodic equilibrium state. Space plasma observations clearly indicate the presence of ion and electron populations that are far away from their thermodynamic equilibrium.[30–35] A new statistical approach, namely nonextensive statistics, is proposed to study the cases where Maxwell distribution is deemed to be inappropriate. The rapidly growing interest to survey the effect of nonextensivity of plasma particles on any nonequilibrium plasma system is due to the fact that such effects of nonextensivity of plasma constituents are quite common in astrophysical and cosmological scenarios. After the rudimentary concept of nonextensive entropy proposed by Renyi[36] and subsequently proposed by Tsallis,[37] the nonextensive behavior of electrons and ions has been successfully employed in plasma physics.[38–40] Liu et al.[41,42] show that when q < 1, the plasma described by the q-distribution contains a plentiful supply of superthermal particles; when q > 1, it contains a large number of low velocity particles. Recently, Ema et al.[43] and Li et al.[44] investigated the propagations of dust ion-acoustic solitary waves in a multi-component dusty plasma with nonextensive distributed electrons and inertial negative ions. Their analysis supports the existence of either compressive or rarefactive solitary waves depending on the plasma parameters.
The aim of this study is to investigate the nature of small amplitude DLs in a collisionless four-component unmagnetized dusty plasma system consisting of nonextensive electrons, inertial negative ions, Maxwellian positive ions, and negatively charged static dust grains. We are interested to apply the Sageev pseudo-potential approach and the reductive perturbation method, because the qualitative behaviors of double-layers are most easily seen. Moreover, we aim to investigate the effects of the compositional parameters such as Mach number, non-extensive parameter, negative-to-positive ion number density ratio, etc. on the formation of the double layers.
The paper is organized as follows. In Section
We consider a collisionless four-component unmagnetized dusty plasma system containing nonextensive electrons, inertial negative ions, Maxwellian positive ions, and negatively charged static dust grains. In such a system where the electrostatic force plays a major role, so the forces coupled with other components of the system can be ignored. Thus, the equilibrium condition reads np0 − nn0 − ne0 − Zdnd0 = 0, where ne0, np0, nn0, and nd0 are the unperturbed number densities of the electron, positive ion, negative ion, and immobile dust, respectively, and Zd is the number of electrons residing onto the dust grain surface. The number densities of q-distributed electrons, and Maxwellian positive ions are,





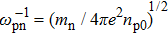
To obtain the travelling wave solutions of Eqs. (




(i) V(ψ) = 0 at ψ = 0 and ψ = ψm.
(ii) dV(ψ)/dψ = 0 at ψ = 0 and ψ = ψm.
(iii) d2V(ψ)/dψ2 < 0 at ψ = 0 and ψ = ψm.
In this Section, we present nonlinear analysis on the DLs solution obtained by the reductive perturbation method.
First, the reductive perturbation method is used to derive the KdV equation[43]


Second, if q is around its critical value qc, the reductive perturbation method is used to derive the higher order nonlinear equation, namely the Gardner equation[43]


Before analyzing the stationary solution of the Gardner equation, we first introduce a transformation ζ = ξ − U0τ, which allows us to write Eq. (






In this section, we numerically analyze the impact of different plasma parameters on the small amplitude ion-acoustic DL structures in an electronegative plasma. It is known that the conditions (i)–(iii) of the Sagdeev potential must be satisfied for DLs. Now, condition (iii) gives the lower limit of Mach number for the existence of DLs as M > MC where

Thus the existence condition, M > MC for DLs, reduces to the condition that the true Mach number M/MC > 1. Henceforth, the true Mach numbers have been used for plotting different figures. V(ψ) are plotted for different values of M/MC in Fig.
 | Fig. 2. (color online) Variation of Sagdeev-like potential profile V(ψ) for DL structures against ψ for different values of M/MC. (a) q = 4.2 and (b) q = 5.0. Here, μn = 0.6, μe = 0.05, and σ = 0.01. |
In Figs.
The variation of ψm and M/MC with q for different values of μn = 0.5, 0.6, and 0.7 is shown in Fig.
In this paper we have investigated the nature of small amplitude DLs in a collisionless four-component unmagnetized dusty plasma system consisting of nonextensive electrons, inertial negative ions, Maxwellian positive ions, and negatively charged static dust grains. This study is based on applying the Sageev pseudo-potential approach and reductive perturbation method, because the qualitative behaviors of the admissible nonlinear dust ion-acoustic waves in the plasma are most easily seen. Our results show that in such a plasma DL structure, the amplitude and nature depend sensitively on the plasma parameters. In particular, it may be noted that due to the electron nonextensivity and/or the negative-to-positive ion number density ratio, our plasma model supports rarefactive(compressive) dust ion-acoustic DLs. Interestingly, one finds that as the electron nonextensivity q increases, the negative dust ion-acoustic DL shrinks and beyond a certain critical value qc, develops into a positive structure allowing therefore the existence of compressive dust ion-acoustic DLs. This critical value is lowered as the number of negative ions becomes important. We hope our results may be useful to explain the basic features of a nonlinear structure in the cometary comae, neutral beam sources, as well as the Earth sheet plasma region where such electronegative plasma can exist.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] |





