Nowadays, because of the fundamental interest for studying nonlinear processes in the presence of a strong electromagnetic (EM) field, the interaction of ultrahigh intensity laser pulses with plasma is attracting a lot of attention.^[1–8] With dramatic progress of current laser facilities, laser pulses with high intensity focusing light up to 10²² W/cm² have already been realized.^[9] Further, the laser projects underway, such as Extreme Light Infrastructure (ELI),^[10] and proposed constructions like the Exawatt Center for Extreme Light Studies (XCELS),^[11] the International Coherent Amplification Network (iCAN),^[12] and Vulcan^[13] are expected to achieve focused intensities above 10²³ W/cm². The development of laser facilities has motivated the investigation of unexplored regimes of laser–plasma interactions.^[14,15] When the plasma is irradiated by such intense laser pulses, quantum electrodynamics (QED) effects become important,^[16,17] and ultrarelativistic dense plasma can be produced. As one of the fundamental QED effects, electron-positron (e⁻e⁺) pair plasma production is highly concerned worldwide,^[18–23] which is potentially interesting for a wide range of applications, such as particle physics,^[24] plasma physics,^[25] and laboratory astrophysics.^[26]

It is demonstrated experimentally that e⁻e⁺ pair plasmas can be produced via the Bethe–Heitler (BH) process from picosecond-class laser pulses (with intensities of 10¹⁸ W/cm²–10²⁰ W/cm²) interacting with mm-thick high-Z target.^[27] However, for low-Z flake and petawatt (PW) laser pulses, the Breit–Wheeler (BW) process dominates over the pair generation due to more efficient productivity.^[21,28,29] In 10-PW laser–plasma interactions, the two main QED effects are the synchrotron γ-photon emission by the nonlinear Compton scattering^[30,31] and the e⁻e⁺ pair generation by the multiphoton BW process.^[32–34] In the nonlinear Compton scattering, e⁻ + nγ_l → e⁻ + γ_h, electrons from the target oscillate in the laser EM field then radiate high-energy photons (γ_h), where γ_l is a laser photon. The radiated photons can further absorb multiple laser photons to emit e⁻e⁺ pairs, γ_h + mγ_l → e⁻ + e⁺, where the number of absorbed laser photons is m → ∞.^[35] When the parameter χ₀ = [(ε₀ + p₀)E₀]/m_eE_cr ≳ 1 (units with ħ = c = 1 are used),^[32] where E₀ is the laser electric field amplitude, V/m is the critical electric field of QED, c is the light velocity, ε₀, p₀, m_e, and e are the initial energy, momentum, mass, and charge of an electron (positron), respectively, the quantum radiation reaction (RR) effect becomes important, and ultrarelativistic electrons (positrons) in the EM field can emit photons incoherently and lose energy.^[30] In the process of ultra-intense laser pulses interacting with plasma, the significance of synchrotron emission and pair generation are determined by the parameters η and χ, respectively, and the two parameters depend on the EM field.^[32,33] Note that the production of e⁻e⁺ pair plasmas can affect the pair plasma dynamics, and the QED processes will in turn affect the EM field. In the scenario of two counter-propagating laser–solid interactions (two-side irradiation scheme), as the results of symmetrical compression of the solid, the formation of electric potential and standing wave (SW) around the target, the QED processes are more remarkable than the scenario of one-side laser–solid interaction.^[36,37] Therefore, the physics associated with the dynamics of pair plasmas in a two-side irradiation scheme is of paramount importance that may shed light on the interplay between strong-field QED processes.

In this paper, we study the e⁻e⁺ pair plasma generation and its dynamics in interactions of two QED-strong linearly polarized laser pulses with a tenuous solid, where the RR effect is taken into account. With the stable SW field formed directly by the two counter-propagating laser pulses in the two-side irradiation scheme, the periodical modulation effects of the SW field on the average energy, spatial, phase-space, and angular distributions of the pairs are demonstrated. We also observe that the RR effect contributes to the trap of dense pair plasmas at the nodes of the SW field. Benefiting from the trapping effect, the two-side irradiation scheme could result in the formation of dense pair plasmas, following the Maxwellian spectral distribution with an average Lorentz factor of γ_AV ≥ 400. Moreover, under different polarized laser pulses, the angular distribution of particles always contracts along the laser polarization direction as long as the SW field exists.

Two-dimensional (2D) simulations are performed by using an open-source particle-in-cell (PIC) code EPOCH^[38] including nonlinear Compton scattering and multiphoton BW process, allowing self-consistent modeling of laser–plasma interactions in the near-QED regime. Two linearly polarized laser pulses propagate along, respectively, the +x direction and −x direction. A set of laser intensities (I = 1 × 10²³ W/cm²–8 × 10²³ W/cm², i.e., 3 PW–25 PW) are taken in the simulations. The laser pulses have transversely super-Gaussian spatial profiles with an electric field as ∝ exp[−(y/1 μm)¹⁰], focusing to spots with a radius of r = 1 μm, and their wavelengths are λ₀ = 1 μm (period T₀ = λ₀/c = 3.33 fs). Besides, we set a flake with a fixed initial density of n_e = 280n_c (n_c = 1.1 × 10²⁷ m⁻³ being the nonrelativistic critical density) to the longitudinal center of the simulation box. The size of the simulation box is 9 μm × 8 μm in the x × y directions. The target plasma has a thickness of 1 μm, and consists of fully ionized carbons and hydrogens with a density ratio n_e : n_C : n_H = 7 : 1 : 1, which is represented by 500 macro electrons and 16 macro ions per cell (single cell size is 10 nm).

Figures 1(a)–1(b) show the temporal evolutions of total positron (BW-electron) number over different laser intensities. For the laser intensity of 4 × 10²³ W/cm², we see that the number of positrons (BW-electrons) increase exponentially after they are produced, but the rapid growth rate is replaced by a slow growth rate when t ≳ 8T₀. We further extract the averaged energy of positrons (BW-electrons), as shown in Figs. 1(c)–1(d). At the initial stage of the pair production, an irregular variation of the positron (BW-electron) energy is displayed. However, at 7.5T₀ < t < 12T₀, the averaged energy of positrons (BW-electrons) oscillates periodically, the lower energies always appear at t = nT₀/2, and the higher energies appear at t = [(2n + 1)/4]/T₀ (n is an integral), indicating a regular modulation effect. Such an energy oscillation can maintain a few periods until t > 12T₀, then the oscillation becomes weaker and finally disappears.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (color online) Temporal evolution of the total number of (a) positrons and (b) BW-electrons. Ensemble-averaged energy evolution for (c) positrons and (d) BW-electrons. The counter-propagating laser pulses at three different intensities, I = 1 × 1023 W/cm2 (black pentagon), I = 4 × 1023 W/cm2 (red circle), and I = 8 × 1023 W/cm2 (blue diamond), are used to irradiate a 1-μm CH foil (ne = 280nc) from opposite sides.

The modulation effect of pair energy can be understood as follows. At the initial interaction stage, SW fields formed on each side of the target by the overlap of the incident and reflected laser pulses are not stable and the RR effect is not significant. When the target becomes relativistic transparent, however, a stable SW field can be formed by the counter-propagating laser pulses directly. The SW field strength is temporally at maximum at t = nT₀/2, and the RR effect is strong enough to drive the ultrarelativistic pairs to losing lots of energies. As a result, the averaged energy of e⁻e⁺ pairs decreases and the decelerated pairs can be readily trapped to the nodes of the SW field, as discussed later. In contrast, when the SW field strength is relatively small at t = [(2n + 1)/4]/T₀, the RR effect becomes weaker accordingly, which improves the pair energy. Afterwards, with the decline of the laser field, the energy oscillation caused by the competition between the radiation loss and field acceleration fades away. In Fig. 1(d) we can see that the final energy of BW-electrons approaches a median value, approximately 200 MeV. Meanwhile, the final positron energy is higher than the BW-electron energy due to the further acceleration from the sheath field generated by fast electrons left from the target, as shown in Fig. 2(a).

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. (color online) (a) Energy spectra of target electrons (red), positrons (blue), and BW-electrons (black). The inset shows the corresponding γ-ray spectrum. Laser intensity of 4 × 1023 W/cm2 and target electron density of 280nc are used. (b) Energy spectra of positrons recorded by two incident lasers with intensities of 1 × 1023 W/cm2 (black), 4 × 1023 W/cm2 (red), and 8 × 1023 W/cm2 (blue), illuminating thin foil with density ne = 280nc. All these data are taken from the same moment of t = 13.25T0.

In addition, for the laser intensity of 8 × 10²³ W/cm², the modulation effect occurs slightly earlier, and the pair number, averaged energy, and the oscillation amplitude appears to be higher than that for lower laser intensities. Because a laser pulse with higher vector potential would drive earlier plasma transparency and better particle acceleration, accordingly, the stable SW field is formed sooner and the RR effect acts more violently. It is also shown in Figs. 1(c) and 1(d) that as the interaction goes on, pair plasmas produced by laser pulses of higher intensity have a visible decrease in their average energy, which is due to the stronger radiation loss in more significant QED effects. Note that the energy oscillation becomes insignificant for lower intensity of 1 × 10²³ W/cm². This is attributed to the fact that the interaction is in the relativistic opaque regime, in which there only exists unstable SW fields formed by the incident and reflected laser pulses, and the QED parameters η and χ are very small.^[39] Therefore, only a few e⁻e⁺ pairs are generated and the energy modulation is invisible.

The difference between the final energies of positrons and BW-electrons can be seen more clearly through the distribution of particle spectra. Figure 2(a) shows the spectral distributions of target electrons, γ-ray photons, positrons, and BW-electrons at t = 13.25 T₀, at which the laser field almost vanishes. In this simulation, laser pulses with an intensity of I = 4 × 10²³ W/cm² are adopted. The spectra of the positrons and BW-electrons are very similar to relativistic Maxwell distributions, which are very close to those observed in the astrophysical jets.^[40] BW-electrons have the same value in the cut-off energy as target electrons, which is ∼ 150 MeV lower than the cut-off energy of positrons. Further, the average energy of BW-electrons (186 MeV) is slightly smaller than that of positrons (224 MeV), also shown in Figs. 1(c) and 1(d). This is attributed to the post acceleration of the sheath field on positrons after the direct acceleration of the laser field. The sheath potential calculated in the simulation is on the order of magnitude of 10⁸ V, doing work Φm_ec², which approximately equals to the difference between the cut-off energies of electrons and positrons. Figure 2(a) also shows that the created pairs within a high-energy region (for example, γ_e ≥ 1000) have comparable charges with those of target electrons, implying that pair plasmas have been involved in the cascade generation of γ-rays. Besides, similar spectral patterns peaking around 150 MeV are obtained under different laser intensities, as shown in Fig. 2(b). The average positron energy is further calculated to be 210 MeV–225 MeV, leading to an average Lorentz factor as large as γ_AV ≃ 440. However, at a laser intensity of 1 × 10²³ W/cm², only a few positrons with low energies are produced, which are hardly discerned from the energy spectrum.

Besides the periodical oscillation of the pair energy, the SW field can also contribute to the modulation on the spatial density distribution of pairs, as shown in Figs. 3(a) and 3(b). At the moment of t = nT₀/2, the high strength electric field is able to drive strong radiation loss, causing many pairs to be trapped to the nodes of the electric field in the SW. The strength of the electric field is always zero at nodes of x = (2n + 1)λ₀/4, and has a maximum at antinodes of x = nλ₀/2, where n is an integer. Therefore, as shown in Fig. 3(a), stripe-like distributions along the laser polarization direction are formed, which have a space interval of λ₀/2. However, when the field strength is relatively weak at moment t = (2n + 1)T₀/4, the trapped pairs become released, and the bunched pattern evolves into a chaotic lobe, as shown in Fig. 3(b).

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. (color online) The spatial density distributions of positron (upper part) as well as electric fields Ey (lower part) at (a) t = 10T0 and (b) t = 10.25T0. Due to the axial symmetry of the distributions, only half of the spatial distributions for positrons and electric fields are plotted. The longitudinal distributions of positron density with consideration of radiation reaction (red) and without radiation reaction (grey) at (c) t = 10T0 and (d) t = 10.25T0. A laser intensity of 4 × 1023 W/cm2 and a foil density of ne = 280nc are used in the simulations.

To show the influence of the RR effect on the pair trapping effect, we present the longitudinal distributions of positron density for simulations with/without RR at t = 10T₀ (Fig. 3(c)) and 10.25T₀ (Fig. 3(d)). It is shown in Fig. 3(c) that when the RR effect is accounted, the positron density peaks at the electric field nodes with a maximum density of ∼ 8n_c. However, in Fig. 3(d), instead of being focused only in the electric field nodes, more positrons tend to appear in the subspace between two nodes. When the RR effect is ignored, the trapping effect is not obvious, and the density difference between the presence and absence of RR at t = 10.25T₀ is smaller than the case at t = 10T₀. This suggests that the SW field and RR effect have a dramatic modification on the positron spatial distribution.

The motion of a free electron (positron) in a laser field is dp/dt = F_L + F_RR, where F_L is the Lorentz force, F_RR is the RR force, and p is the particle momentum.^[41] Contending between the two forces, the pair momentum can also be modulated. As shown in Fig. 4(a), when the SW field is strong, the x–p_x distribution of pairs has a transversely periodical stripe structure, which agrees with its spatial pattern shown in Fig. 3(a). Pairs in these stripes are accumulating in the region of the SW instead of being expelled transversely by the ponderomotive force. Consequently, their y–p_y distribution displays a bright elliptical pattern in the center, as shown in Fig. 4(b). However, the pair dynamics is different when the SW field is relatively weak. The confinement of SW on pairs is lost, therefore, pairs with p_x > 0 move along the +x direction, yet those with p_x < 0 tend to move backward. As a result, the transverse stripe structure becomes oblique with respect to the longitudinal direction, as shown in Fig. 4(c). The weakened SW field further disperses the pairs in the phase-space of y–p_y, since the RR effect becomes insignificant so that it is difficult to compensate their transverse dispersions.

Fig. 4.

	Figure Option ViewDownloadNew Window
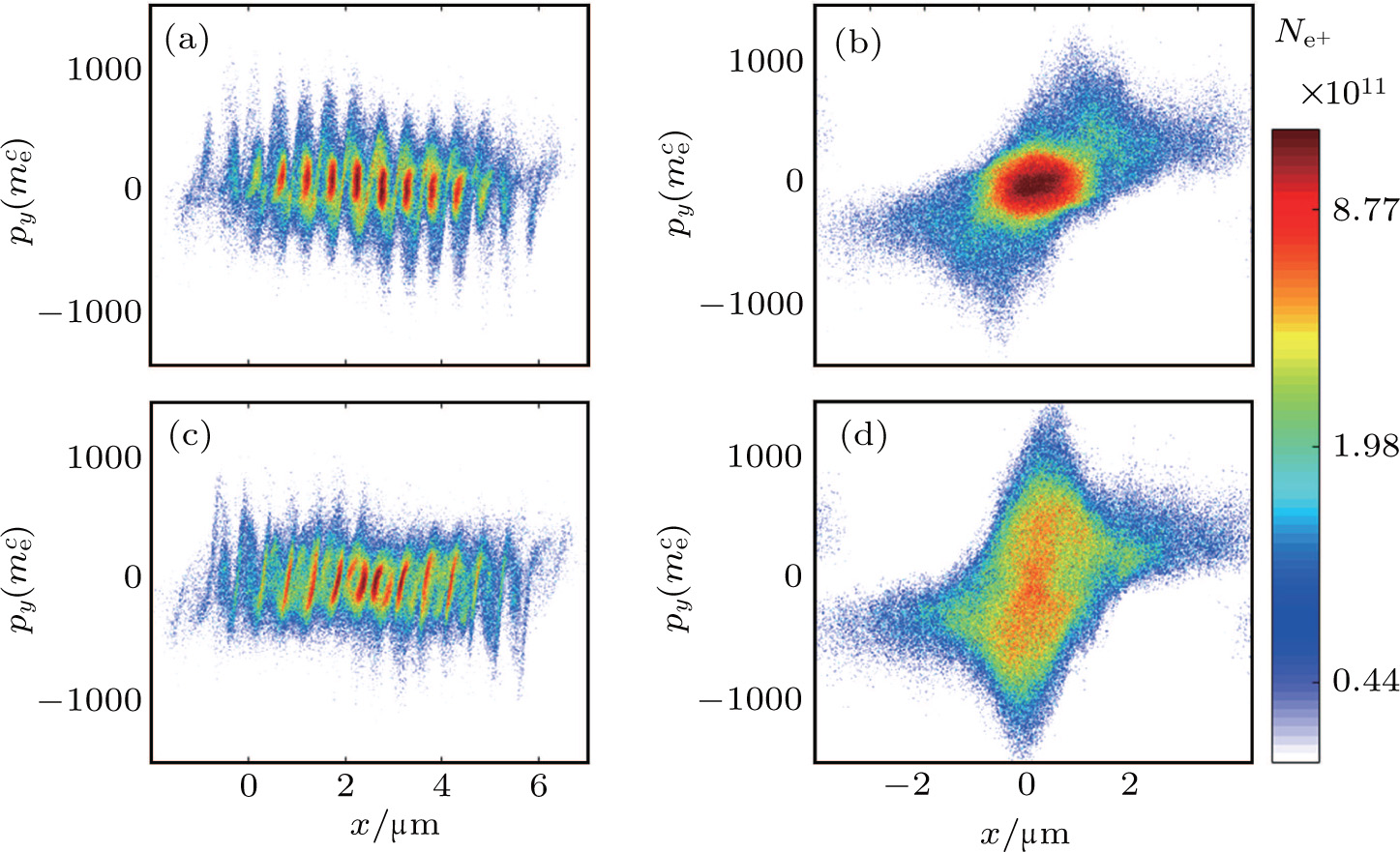	Fig. 4. (color online) Positron phase-space distributions for x–px at moment (a) t = 10T0 and (c) t = 10.25T0, and for y–py at (b) t = 10T0 and (d) t = 10.25T0.

In the following, we perform a series of simulations to investigate angular distributions of target electrons, γ-photons, and e⁻e⁺ pairs. Since it is necessary to consider additional plasma effects, such as thermal expansion along the z direction, more simulations are conducted. We define θ = 0° along the direction of the laser propagation, and φ = 0°(90°) along the direction of p (s)-polarization. In Fig. 5(a), the modulations of the polar distribution on the pair plasma intensity are visibly displayed. The two-side irradiation scheme enables irradiating and compressing a thin foil more symmetrically, thus target electrons, γ-photons, and positrons have symmetric θ-intensity patterns with respect to the azimuthal plane. It is noteworthy that the relativistic e⁻e⁺ pairs are moving in a figure-of-eight trajectory rather than in straight lines like other particles, which is because they quiver nonlinearly in the QED-strong field.

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. (color online) (a) Polar distributions of target electron, γ-photon, and positron intensities at times t = 10.0T0 and 10.25T0 and (b) polar distributions of target electron, γ-photon, BW-electron, and positron intensities at t = 14.5T0, for p-polarized laser. Azimuthal distributions of target electron, γ-photon, and positron intensities at t = 10.0T0 and 10.25T0, for (c) p- and (d) s-polarized lasers. In panels (a), (c), and (d), the black, cyan, and blue solid lines represent target electrons, γ-photons, and positrons, respectively, at t = 10.0T0; the magenta, green, and red dashed lines indicate target electrons, γ-photons, and positrons, respectively, at t = 10.25T0; the polar distribution of BW-electron intensity displays a similar pattern as that of the positron, thus is not shown here.

In the presence of the SW field, the polar patterns of positrons at t = 10.0T₀ and 10.25T₀ are pinched along the direction of the laser polarization due to the aggregation effect of the SW field. The polar pattern at t = 10.0T₀ becomes slimmer relative to that at t = 10.25T₀. This is due to a tighter confinement effect along the longitudinal direction of SW. In order to confirm such an effect, we display in Fig. 5(b) that when the SW field fades at t = 14.5T₀ the pinched effect disappears. It is also shown in Fig. 5(b) that different from BW-electron, the positron intensity has an anisotropic distribution due to the influence of sheath acceleration. For p-polarized lasers, target electrons experience transverse electric fields. These electrons and photons emitted by them have the tendency to move along the laser polarization direction, i.e., θ = 90°, see Figs. 5(a) and 5(b).

Figures 5(c) and 5(d) show azimuthal distributions of the target electron, γ-photon, and positron intensities for p- and s-polarized lasers, respectively. In both laser polarization cases, target electrons have angular patterns with maximal intensity in their laser polarization directions respectively. However, such a pattern is a little fat as a result of the target thermal expansion after being symmetrically compressed by laser radiation pressures. The azimuthal distribution of γ-photon intensity peaks on-axis of the laser polarization, suggesting a high-dense photon generation based on the Compton scattering effect in the highly nonlinear regime. The positron intensity displays similar patterns as the γ-photon. It is also shown in Figs. 5(c) and 5(d) that temporal evolutions of the SW field can hardly affect the positron azimuthal pattern, which is different from the modulation dynamics of positron polar structure.

In summary, 2D simulations are performed to investigate the generation and modulation dynamics of pair plasmas in the interactions of two counter-propagating ultra-intense laser pulses with a thin solid target. The average energy, spatial, phase-space, and angular distributions of pair plasmas can be modulated periodically after the interaction enters the relativistic transparency regime. Based on the synergy of the SW field and the RR effect, the average energy of pairs is oscillating significantly, and the pairs are trapped at the nodes of the SW field with an interval of 0.5T₀. Despite different laser polarizations, the angular distribution indicates that the particles always have a tendency to move along the laser polarization direction, and the pinch effect on pairs only appears when the SW field exists. However, when the interaction is in the relativistic opacity regime, such modulation effects do not exist. With the worldwide upcoming 10 PW-class laser systems, the modulation dynamics reception of pair plasmas is expected to be helpful in the future experimental investigation of pair plasmas at approachable laser intensities in current laboratories.