† Corresponding author. E-mail:
Ion population fraction (IPF) calculations are very important to understand the radiative spectrum emitted from the hot dense matter. IPF calculations require detailed knowledge of all the ions and correlation interactions between the electrons of an ion which are present in a plasma environment. The average atom models, e.g., screened hydrogenic model with l-splitting (SHML), now have the capabilities for such calculations and are becoming more popular for in line plasma calculations. In our previous work [Ali A, Shabbir Naz G, Shahzad M S, Kouser R, Rehman A and Nasim M H 2018 High Energy Density Phys.
The simultaneous presence of multi-charge ions in hot and dense plasmas predicted by radiative spectra in different experiments is of critical importance.[1] This is closely relevant to the astrophysical plasma, the plasma found in giant planets like Jupiter, and the plasma created in the inertial confinement fusion (ICF) experiments.[2,3] The calculations of ion population fractions (IPF) are very important for many thermodynamic and radiative properties of such hot dense plasmas. These calculations start with the construction of grand partition function (GPF) for interacting electrons in hot and dense plasma. The GPF contains all the information of how different ions have their energy partitioned among themselves in hot dense plasma. The simplest form of GPF is its construction for Fermi gas, where the particles are not interacting among themselves, and then GPF is developed for hot dense plasma for interacting electrons. Now this GPF contains information of the level population, level charges, and level energies of interacting electrons. Finding the solution of this GPF (to make it factorizable) for the interaction electrons (the case of hot and dense plasma) over all possible configurations is not a trivial task as that can be done in the case of non-interaction electrons. In the latter case, a close form of the generating function can be obtained or we can easily factorize the GPF. However, for the interacting electrons systems, the number of terms in GPF increases rapidly and we have to define some cut-offs on the electron population to get reasonable results. Thus it would be difficult to factorize GPF due to the presence of cross-interaction terms for different electrons of a configuration and due to the conservation of the number of electrons for each charge state in a consistent manner. For this purpose, a detailed atomic code would be needed that include all relevant atomic physics processes for the calculation of electron populations for different ions. These models are broadly divided into detailed level (DL) models[4,5] and average atom (AA) models.[6–8] Another class of models uses a parametric potential method to generate speedy atomic data as implemented in Los Alamos National Laboratory code OPAL.[9] There is a new development on the theoretical basis at Los Alamos implemented in code ChemEOS,[10] which is based on a chemical picture representation for a plasma of interacting ions, atoms, and electrons. This code uses the free-energy-minimization technique for Helmholtz free energy of the interacting species to get thermodynamic functions for the equation of state (EOS) and IPF for the opacity calculation in the ATOMIC code.[11]
The average atom models are becoming more popular for hot and dense plasma studies. This is due to the fact that these models can be used for in-line calculations of the equation of state and opacity data contrary to the detailed leveled atomic calculations. Different versions of AA are proposed in the literature depending upon the form and model of the potential used in calculations and boundary conditions imposed on it. All these models have some limitations and approximations based on accuracy and speed. These versions of AA models are used in different standard codes, e.g., Thomas Fermi model (TF), quantum statistical model (QSM), or quantum self consistent field (QSCF) as referred in Ref. [12] are used in codes THERMOS, CASSANDRA,[13] OPAQS,[14] etc. Another famous class of AA models is based on the finite temperature density functional theory (FTDFT) which is basically an electron density variational model[15,16] based on KhonSham equations developed in codes like multi average ion model (Multi-AIM),[17] while AA model based on screening constants, i.e., screened hydrogenic model with l-splitting (SHML)[18,19] for the construction of hydrogenic potential is used in codes like ATMED,[20] SCAALP,[21] etc.
These models represent an average electron population for a given temperature and density and do not include different ionization stages, therefore, they cannot be used to study the experimental spectroscopic data. Using AA models for such studies started with Green,[22] who calculated the correlation energy and population levels for interacting electrons for using an average atom prescription under local thermodynamic equilibrium (LTE) conditions, and the complex operators was used to form GPF for such system. Another attempt was made by Perrot,[23] who calculated the correlation energy by minimizing the Helmholtz free energy using density functional theory (DFT) for the AA model. He has included the bound–bound, bound–free and free–free electron interaction contributions to the calculation of IPF. Wilson[24] introduced the saddle point technique for correlation energy calculations. In this method, GPF summation is transformed into multidimensional integrals from which it is easier to get IPF. This work was extended by Faussurier[25,26] by proposing classical theory of fluctuations in saddle point technique for the calculation of IPF.
Faussurier[25,26] proposed his version of screened hydrogenic model with l-splitting for the in-line calculation of EOS and opacity for high energy density system, and included IPF calculation by improving the saddle point technique. We have improved this SHML model, I-SHML,[27] regarding continuum lowering potential calculations, and by including the exchange and correlation effects to study the density effect in high energy density systems. We have also developed a computer code named OPASH by implementing this improved version of SHML and presented the results for average charge state calculations for different plasma conditions. In this study, we have included IPF calculation using improved SHML and compared our results with Faussurier model and other models. In the next section, we will briefly describe the I-SHML model and inclusion of IPF calculation will be discussed in Section
We briefly describe the basic ingredients of SHML[18,19] model and the improvements made by us to lay down some mathematical notation for the next section. SHML is basically an AA model based on the central field approximation in which each electron of a level k (k = 1 + lk + nk(nk − 1)/2, where nk is the principal quantum number and lk is the angular momentum quantum number) moves in an independent effective hydrogenic potential characterized by Zk/r, where Zk is the level screened charge with limitation of 1 ≤ k ≤ kmax. kmax is the maximum number of orbitals considered in the calculation, which in our case is 55 corresponding to all levels up to n = 10. In AA the electrons in different levels are not statistically correlated and can be characterized by a fixed number of states, each with a fixed electron occupation number (not necessarily an integer), i.e., a fixed electronic configuration 
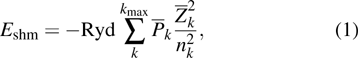
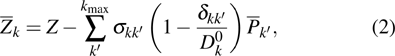










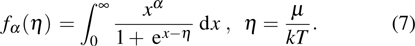


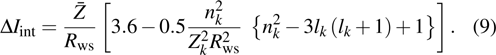





The simultaneous presence of different ions in plasma cannot be modeled directly within the AA approximation. In order to model IPF in hot dense plasma using the AA model, one starts with the quantum statistical representation of GPF which is written in terms of energy levels of the particles within GFP. The energy levels further require the information of number of particles, their population level, and the corresponding charge. Formally, the ion population fractions were calculated by using isolated atom data of energies in Saha–Boltzman equation, with CL taken into account along with some empirical cut off for the partition function. The problem with Saha–Boltzman equation is that it breaks down at higher ion densities.[32] Moreover, Saha–Boltzman is limited for non degenerate electrons at high temperature and low to moderate densities. The inclusion of different configurations interactions has been added which improves the results but does not solve the problem of the breakdown for higher densities. Another approximate solution is the use of binomial distribution for ion population fraction, which is based on the ideal Fermi Dirac gas model, e.g, used in NIMP model (non LTE ionized material package).[33] But that itself is based on the fact that there is no correlation between electron probabilities which are dominant at higher densities and at low temperature. The result for binomial distribution and Saha Boltzman distribution matches for the low density and very high temperatures, but fails to predict the average charge state and IPF results at lower temperatures and at higher densities where strong interactions between electrons are dominant. Moreover, isolated energies are used under the approximation that the kinetic temperature is comparable to the isolated energies, which is questionable to date.[25,26] For the development of IPF in I-SHML, we follow the work of Ref. [25] for the development of the systematic integer charge state distribution around the average charge state using classical theory of fluctuations. The detailed derivation and discursion of these equations can be found in Ref. [25] as well as Refs. [34] and [35]. According to Ref. [25], the GPF for Z + 1 ion system can be factorized and is given by









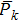









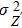

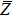
We have implemented the IPF calculations using Eqs. (
We have compared the results of our model with several other models as well. The most important is the model of the Kiyokawa[17] that uses a multi average ion (Multi-AIM) formulism developed for hot dense plasma. Multi-AIM uses finite temperature density functional theory (FTDFT), in which pair correlation functions are obtained self consistently by minimizing the free energy of the system. They have also included the exchange and correlation potentials in their calculations, and self consistency for IPF is achieved using Saha equation. We have compared our results of IPF for low density (0.0081 g/cc) iron plasma at different temperatures with Multi-AIM model in Fig.
 | Fig. 6. (color online) Ion population fractional of average ions in an Al plasma at an ion density of 2.77 g/cc and a temperature of 100 eV, where the red line indicates that obtained by Multi-AIM, the blue line indicates Perrot’s result,[37] and the black line is for the binomial distribution. The I-SHML results are drawn by the wine color and sea green lines that stand for the cases with and without correlation, respectively. |
In Fig.
 | Fig. 8. (color online) Comparison of IPF of I-SHML with the ChemEOS code for iron at an ion density of 1023 and at a temperature of 192.91 eV. |
The comparison of I-SHML calculations with ChemEOS model is presented in Fig.
 | Fig. 9. (color online) Comparison with detail level calculation of Ref. [38] for aluminum plasma at a temperature of 400 eV and at different densities of 1 g/cc (a), 5 g/cc (b), and 20 g/cc (c). |
The IPF calculations for the hot dense matter are very important to understand the emitted complex radiative spectra from the experiments which show the presence of different ions with composite electronic structures. These multiplex electronic structures in dense plasmas are due to CL phenomenon which arises due to the interaction between bound and free electrons. The calculation of IPF involves the solution of GPF for interacting electrons, which is obtained either from DL calculations or by the AA model using classical theory of fluctuations. In this study, we present the IPF calculations under the LTE plasma conditions based on classical theory of fluctuations using I-SHML which contains the improved form of CL. The results of IPF computations for aluminum and iron are compared with the published literature of Saha model and binomial distribution models, and are correspondingly discussed. Good agreement is found for high temperature and low density plasma conditions with binomial and Saha models. Some deviations are seen for low temperature and high density plasma conditions where there are strong correlation interactions which are not addressed in binomial and Saha models. Our results gives good estimate for IPF over a wide range of densities and temperatures due to the presence of CL and correlation effects.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] |








