† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11372141 and 11472138) and the National Defense Pre-Research Foundation of China (Grant No. 61426040201162604002).
Acoustic characteristics of a pulse detonation engine (PDE) with and without an ellipsoidal reflector are numerically and experimentally investigated. A two-dimensional (2D) non-splitting unstructured triangular mesh Euler solver based on the space-time conservation element and solution element (CE/SE) method is employed to simulate the flow field of a PDE. The numerical results clearly demonstrate the external flow field of the PDE. The effect of an ellipsoidal reflector on the flow field characteristic near the PDE exit is investigated. The formation process of reflected shock wave and reflected jet shock are reported in detail. An acoustic measurement system is established for the PDE acoustic testing. The experimental results show that the ellipsoidal reflector changes the sound waveform and directivity of PDE sound. The reflected shock wave and reflected jet shock result in two more positive pressure peaks in the sound waveform. The ellipsoidal reflector changes the directivity of PDE sound from 20° to 0°. It is found that the peak sound pressure level (PSPL) and overall sound pressure level (OASPL) each obtain an increment when the PDE is installed with a reflector. The maximum relative increase ratio of PSPL and OASPL are obtained at the focus point F2, whose values are 6.1% and 6.84% respectively. The results of the duration of the PDE sound indicate that the reflecting and focusing wave generated by the reflector result in the increment of A duration and B duration before and near focus point F2. Results show that the ellipsoidal reflector has a great influence on the acoustic characteristic of PDE sound. The research is helpful for understanding the influence of an ellipsoidal reflector on the formation and propagation process of PDE sound.
The pulse detonation engine (PDE) is an innovative propulsion technology that could potentially provide significant advantages, such as mechanical simplicity, higher thrust-to-weight ratio, lower cost, high thermodynamic cycle efficiency, and a wide working scope. Much progress has been made in many important performance aspects of PDEs.[1] In order for the PDE to be commercially successful as a propulsion device, the environmental effect of the PDE should be considered as an important issue. When the detonation products are directly exhausted from the detonation chamber to the ambient environment, part of the chemistry energy of fuel is converted into acoustic energy instead of being converted into the kinetic energy to produce thrust. However, relatively few researches have been published on PDE acoustics. The preliminary studies provided an initial understanding of PDE acoustic behavior.[2–9] The PDE sound is produced by two sources: noise associated with the shock wave, and jet noise produced during the blowdown of hot detonation products.[10] The definition of impulsive noise was brought forward in a China National Standard of GJB50-85, namely, the noise which is composed of one or more abrupt noises (its duration time is less than 1 s) can be called impulsive noise. According to its physical characteristics, the impulsive noise can be classified as two kinds. One is the impact noise, which is caused by solid objects impacting, the elasticity vibration, distortion, and rupture, and the other is caused by pulsed pressure which is produced by blast, bang, or turbulence. Obviously, the PDE noise belongs to impulsive noise. The sound radiation characteristics of PDE sound are intermittent, periodic short duration, and high intensity. The noise and vibrations generated by the PDE directly affect aircraft stealth and structure fatigue, thus posing a serious threat to the overall performance and safety of aircraft. It has been suggested that the ellipsoidal reflector used can gather part of the sound energy to the action target, otherwise this energy would radiate to other places. This utility of the ellipsoidal reflector can be used to reduce the noise impact of critical parts of the PDE. The ability of the ellipsoidal reflector to focus acoustic energy will make PDEs have important application prospects in other military fields.
In general, there are three ways to focus sound waves.[11,12] The first is the phased array method. By adjusting parameters such as the delay time, spacing, and emission frequency of each array element, acoustic beams with small side lobes and strong directivity can be formed, thereby forming high-energy beam spot areas at the target point. The phased array can realize the multi-point focusing and any angle deflection of the sound beam without an auxiliary mechanical rotating device. The second is the acoustic lens method. By using special materials and design structures, the acoustic wave bends when it passes through the lens, thus achieving a higher intensity at the target point. The third is the surface reflection method. The originally spherical diffused sound wave is reflected as a convergent wave through a curved reflector with special geometric properties, such as rotating parabolic surface and ellipsoid.
Compared with the former two types of acoustic energy accumulation, the reflective energy accumulation is relatively simple. The acoustic energy can be enhanced at the target point by installing a reflector with a special geometry on the sound source. Cates and Sturtevant[13,14] developed a finite-difference numerical method for geometrical shock dynamics based on the analogy between the nonlinear ray equations and the supersonic potential equation. The numerical results exhibited the qualitative behavior of strong, moderate, and weak shock focusing observed experimentally. The results showed that the maximum pressure at focus is influenced by the aperture angle and shock strength. Schaefer and Grapperhaus[15] measured the light and sound emitted by an air sparker-reflector combination. The quantitative measurement results combined with a reflector model indicated that the reflector directs and focuses the sound to deliver high intensity pulses at range. Zhou and Zhong[16] explored the effect of reflector geometry on the acoustic field produced by an electrohydraulic shock wave lithotripter. The pressure wave form generated by the spark discharge was measured and used as a source condition in numerical calculations. An equivalent reflector model was developed and proved to be a useful tool for the prediction of pressure wave form generated in a lithotripter field. However, there is no report on the application of reflectors to PDE sound.
In this study, experimental and computational investigations are performed on a PDE with and without an ellipsoidal reflector. The effects of the ellipsoidal reflector on PDE acoustic characteristics are explored. The acoustic characteristics of PDE, including peak sound pressure level (PSPL), overall sound pressure level (OASPL), directivity and duration, are analyzed. The simulated results can enhance the understanding of acoustic formation mechanisms of PDE sound. It is found that the reflector can reflect and focus the most acoustic energy, which originally points to the upstream direction, in the vicinity of the reflector focus. The installation of the reflector does not enlarge the area affected by PDE sound.
In order to explore the detonation acoustic characteristics of a PDE with an ellipsoidal reflector, the experiment system is set up as shown in Fig.
The acoustic measurement facility is specifically designed for obtaining acoustic data. A circular microphone array of six PCB model 377A12 microphones and 426B03 1/4” preamplifier are arranged at directivity angles of 0°, 20°, 40°, 60°, 75°, and 90° at a radius from 1 m to 50 m away from the PDE exit. The directivity angle is defined as the angle from the microphone with respect to the PDE tube centerline with 0° being assigned to be the downstream direction. The acoustic data of PDE are acquired at 500 k samples/s for all microphones simultaneously.
Figure
It is noticed that there are two important acoustic parameters for various types of impulse noises, peak sound pressure level (PSPL), and overall sound pressure level (OASPL), the former (i.e. PSPL) is universally considered as the most critical factor for human noise-induced hearing loss and is defined as

The latter (i.e. OASPL) is defined as


In order to explore the influence of flow field near the tube exit on PDE acoustic characteristics, a computational analysis model is established. The main difficulty in performing a simulation lies in the complex interaction between two phases of a two-phase detonation in the PDE tube. In this paper, a two-fluid model is chosen for the simulation of two-phase detonation.
To simplify the process of the gas/liquid two-phase detonation, it is assumed that the gas/liquid two-phase pulse detonation engine is axisymmetric in structure; the phase of droplets is considered as a continuous medium; the radii of droplets are uniform and the droplets are homogenously distributed initially; the interactions between droplets can be ignored; each droplet does not break and remains spherical while the detonation propagates; the initial temperature of the gas and the droplets are the same; the shape of each of the droplets always keeps spherical even in the process of separation and evaporation; and when the droplets reach the gaseous state, chemical reactions occur and are accomplished immediately.
Under the above assumptions, the Euler equations for compressible flows in gas/liquid two-phase PDE can be expressed in the conservative form as[17]


There is a constraint of the volume fraction for the two-fluid model: ϕg + ϕl = 1.0, where g and l mean gas phase and liquid phase respectively, ϕg and ϕl denote the volume fraction ratio of the gas phase and liquid phase. In Eq. (
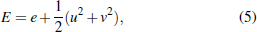


The first term on the right-hand side of Eq. (





Equation (


Figure
The initial pressure and temperature are 1 atm (the unit 1 atm = 1.01325 × 105 Pa) and 298 K respectively. Gasoline/air mixture at a certain stoichiometric ratio is filled uniformly in the PDE tube. The radius of fuel droplets is 50 μm.[20] In order to simulate the initial ignition spark, 15 ambient pressures and 15 ambient temperatures are specified in the range of x/l ≤ 0.01 and r/r0 ≤ 0.5,[21,22] where l is the length of the tube and r0 is the radius of the tube. The external flow field is filled with air at the normal temperature and pressure.
The PDE sound is essentially produced through two sources: noise associated with shock wave and jet noise produced during the blowdown of the detonation products. Figure
 | Fig. 4. (color online) Four snapshots of the pressure contour of PDE external flow field at t = 1.18 ms (a), 1.2 ms (b), 1.8 ms (c), and 3.3 ms (d). |
Figure
 | Fig. 5. (color online) Experimental results of sound pressure of PDE, showing (a) sound pressure of PDE sound and (b) impulse noise pressure history. |
The sound pressure signal is analyzed by the FFT method. Figure
The flow field structure near the PDE exit has a great influence on the formation of a PDE sound wave, so it is necessary to explore the flow field in the near-field region of the PDE. Figure
The first study conducted is to directly compare the acoustic time domain characteristics of PDE and PDE with an ellipsoidal reflector. In the experiments, the equivalence ratio of the fuel and oxidizer mixture, fill fraction, and the operation frequency keep consistent.
Figure
Like the acoustic characteristics of the PDE, sound pressure peaks P1 and P2 represent the direct wave of shock noise and jet noise, respectively. P3 is the ground reflection noise. Sound pressures P4 and P5 represent the wave produced by the reflecting and focusing of shock noise and jet noise. The direct shock noise propagates to the focus point F2 ahead of the reflecting shock noise by 0.86 ms and the direct jet noise arrives at F2 ahead by 2.13 ms compared with the reflecting jet noise. The reason for this phenomenon is the differences in the propagation distance and time of direct wave and reflection wave. However, the value of the focusing shock noise P4, which is 1265.8 Pa, is about 3.7 times that of the direct shock noise. Numerical simulation results show that the focusing shock noise is 3.26 times direct shock noise at 2 m away from the PDE exit. The experimental results show that the focusing shock noise at this testing point is 3.04 times the direct shock noise, which is consistent with the numerical simulation. Due to the limitation of the computational area, the focusing noise and direct noise cannot be calculated at the position of 20 m away from the PDE exit directly, but the calculation results of the linear model of an acoustic wave show that the numerical calculation in the far field is also consistent with the simulation result. The value of focusing jet noise P5 is 539.9 Pa, which is about 2.5 times that of the direct jet noise. As can be seen, there are minor oscillations following the peak pressure P5. This may be caused by the complex flow field structure in the PDE plume.
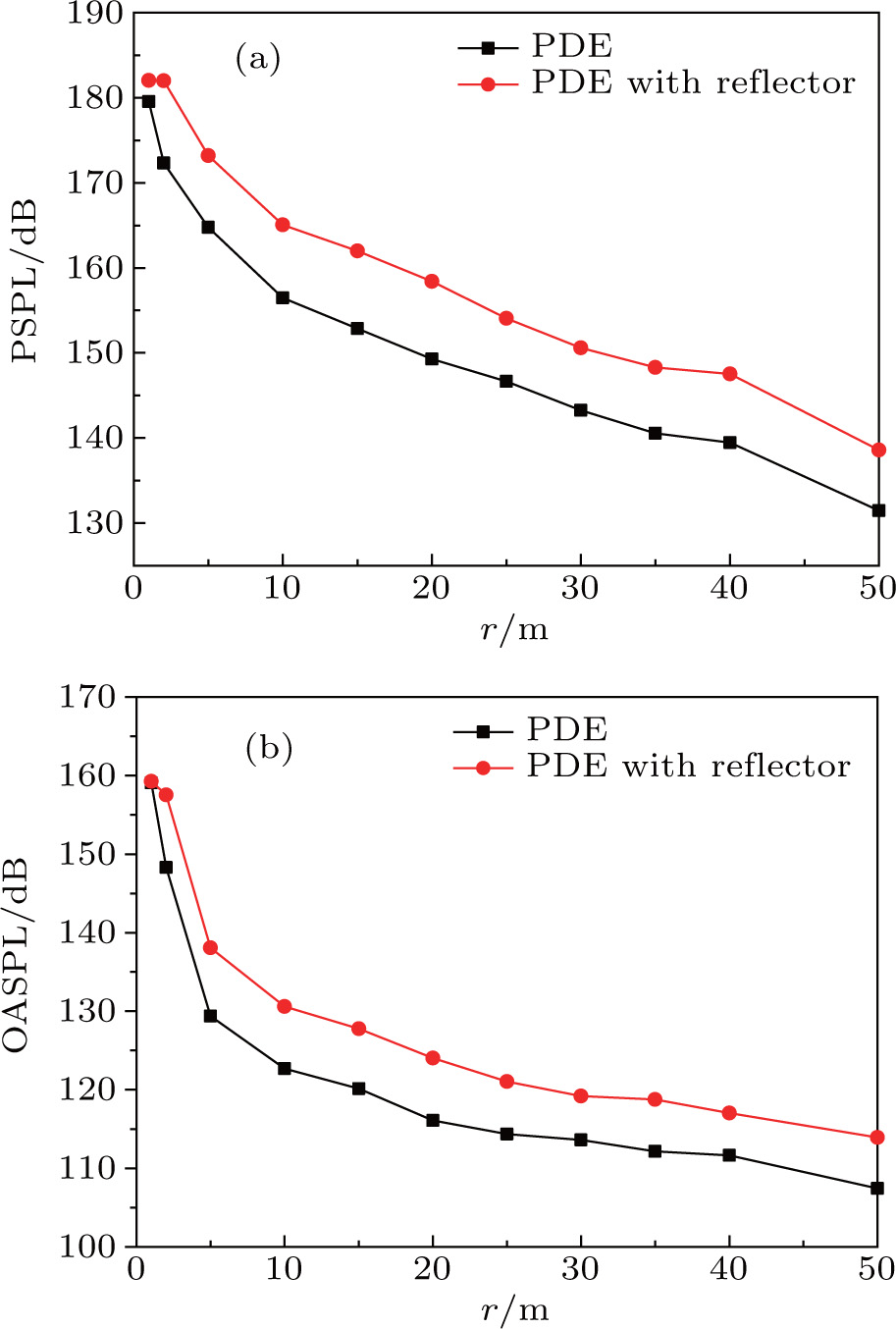
Figure
| Table 1. Effect of ellipsoidal reflector on PSPL and OASPL. . |
The calculated results of the increase and relative increase ratio of PSPL and OASPL of the PDE by the reflector are presented in Table
From the above analysis, it can be seen that the radiation energy of PDE sound has significant differences in different directions. The research on the directivity of PDE sound is of great significance for designing the structure of PDE. A thorough understanding of PDE sound directivity is beneficial to controlling the emission angle of sound for better utilization.
To simplify the study of the variation of directivity of PDE sound, the PSPL of PDE noise is normalized as

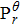
The corresponding PSPL at different angles of PDE sound are shown in Figs.
Hearing impairment and loudness are both related to the energy of impulse noise. When evaluating the energy of impulse noise, the effective duration and the amplitude of sound pressure are equally important. Therefore, the duration becomes another important physical characteristic. Three types of durations are commonly used to assess impulse noise, i.e., A duration (t+), B duration (tB), and C duration (tC). The A duration is the time taken for the initial or principal pressure wave to rise to its positive peak and return momentarily to ambient pressure. The B duration is the total time taken for the envelope of the pressure fluctuations (positive and negative) to be within 20 dB of the peak pressure level.[23] Referring to the definition of impulse noise duration, the A duration and B duration of PDE sound are studied in this research.
Figure 

The A duration and B duration of PDE sound at different axial positions are shown in Figs.
As shown in Fig. 





It can also be noted that 

As shown in Fig.
In this study, the acoustic characteristics of a PDE with and without an ellipsoidal reflector are numerically and experimentally investigated. The formation process of PDE sound is explored by the computational analysis. The PDE sound is essentially produced through two sources: noise associated with a shock wave and jet noise produced during the blowdown of the detonation products. The numerical results clearly demonstrate the flow field structure near the exit of the PDE with an ellipsoidal reflector. The shock wave and jet shock wave originally propagating upstream are reflected by the ellipsoidal reflector and focused in the PDE axis direction. The experimental results show that the ellipsoidal reflector can realize the shock wave noise and jet noise focusing well, and create a focal zone at the PDE axis with very high pressure, and obviously slow down the pressure attenuation along the distance and time in the downstream direction. The maximum relative increase ratio of PSPL and OASPL are obtained at focus point F2 of the ellipsoidal reflector, whose values are 6.1% and 6.84% respectively. The greatest PSPL of PDE sound appears at a directivity angle of 20° while it changes to 0° directivity angle under the installation of the reflector. Due to the focusing wave generated by the ellipsoidal reflector, the time of acoustic pressure beginning to fall turns delayed, resulting in the increase of A duration and B duration before and near focus point F2.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] |