Cite this Article
Liu Xuejing, Yang Luwen, Ma Jingyun, Li Caili, Jin Wa, Bi Weihong. Study on polarization properties of graphene coated D-shaped fiber. Chinese Physics B, 2018, 27(10): 104206  
Permissions
Study on polarization properties of graphene coated D-shaped fiber
Liu Xuejing1, Yang Luwen2, Ma Jingyun2, Li Caili2, Jin Wa2, 3, †, Bi Weihong2, 3
School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China
School of Information Science and Engineering, Key Laboratory for Special Fiber and Fiber Sensor of Hebei Province, Yanshan University, Qinhuangdao 066004, China
Key Laboratory for Special Fiber and Fiber Sensor of Hebei Province, School of Information Science and Engineering, Qinhuangdao 066004, China

 

† Corresponding author. E-mail: jinwa@ysu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 61575170, 61575168, and 61475133), the Basic Research Project of Hebei Province, China (Grant No. 16961701D), the Natural Science Foundation of Hebei Province, China (Grant No. F2016203392), the Provincial College and University Natural Science Foundation of Hebei, China (Grant No. QN2016078), and the Intramural Doctoral Foundation of Yanshan University, China (Grant No. B1011).

Abstract

The optical properties of graphene coated D-shaped single mode fiber and photonic crystal fiber are numerically analyzed. Enhancement of the graphene-light interaction is found in graphene coated D-shaped photonic crystal fiber, which introduces a tunable polarization of the D-shaped fiber by changing the chemical potential of the coated graphene. An optimal polarizer model is demonstrated with the extinction ratio of 66.26 dB/mm and the insertion loss of 9.4 dB/mm. The modulator extinction ratios of the TE mode and TM mode are 11.5 dB and 5 dB, respectively, with a device length of 100 μm. This paper provides a theoretical reference for the optical property research of the graphene fiber.

PACS: 42.79.-e;42.79.Hp;42.81.-I;78.20.Jq
Keyword:photonic crystal fiber;graphene;polarization;chemical potential
1. Introduction

Graphene is attracting worldwide attention due to its unique electronic and photonic properties, such as high quantum efficiency for light-matter interactions, high carrier mobility, zero bandgap, gate-variable optical conductivity, ultra-broadband saturable absorption, and nonlinear optical Kerr effect, which have led to demonstrations of a number of graphene-based fiber devices,[1–3] such as polarizers, saturation absorbers, modulators, switches, photo-detectors, and so on. The graphene-light interaction is limited by a large area of cladding layer for single mode fiber (SMF). The enhancement of graphene-light interaction remains a challenge for many graphene-based photonic devices. Different geometric structures, including polish and taper, have been proposed to efficiently enhance the light-graphene interaction.[4–7]

In this paper, we explore the transmission characteristics of a graphene coated D-shaped fiber and find that a largely enhanced light-graphene interaction is induced by the strong evanescent field of the D-shaped SMF and D-shaped photonic crystal fiber (PCF). It is demonstrated that by employing multi-layer graphene, the light-graphene interaction and modulation effect can be greatly enhanced, which provides theoretical guidance for future experiments.

2. Theoretical analysis

Graphene, a two-dimensional crystal material, is a single atomic layer of sp2-hybridized carbon forming a honeycomb crystal lattice.[8] The hexagonal honeycomb lattice of graphene, with two carbon atoms per unit cell, leads to a rather unique band structure. The bottom conduction band and the top valence band touch at six points, the so-called Dirac points, and there is no energy bandgap, which can be viewed as two cones touching at the Dirac point. This unique band structure determines the simultaneous existence of interband and intraband transitions. Therefore, the conductivity of graphene is described by interband and intraband contributions, with its conductivity given by the Kubo formula[9]

here, ħ is the reduced Planck constant, e is the electron potential, ω is the radian frequency, μc is the chemical potential, τ is the relaxation time (τ1 and τ2 are associated with intraband and interband transitions, respectively), fd (ε) = (exp((ε − μc)/(kT)) + 1)−1 is Fermi–Dirac function, k is the Boltzmann constant, and T is the temperature. Here we set T = 300 K, τ1 = 10 fs, and τ2 = 1.2 ps.[10]σ has a positive imaginary part σ″, which plays an important role in the propagation of surface waves in a graphene sheet. It supports transverse magnet (TM) polarized modes when its imaginary part of the conductivity is positive, while it supports transverse electric (TE) polarized modes when its imaginary part of the conductivity is negative.[11]

3. Analysis of polarization characteristics

Polarizers are indispensable key optical components in optical communication systems, which can realize the conversion and switching of the polarization state. An electro regulation polarizer model based on graphene coated D-fiber is proposed by controlling the Fermi level of graphene. The complex effective refractive index is used to illustrate the optical characteristics of graphene coated D-fiber, and the imaginary part of the effective refractive index is k, the absorption coefficient is α, the limiting loss is Losslimit, the insertion loss is Lossinsert, and the polarization extinction ratio is σPER,[12,13] which are described by the following equations:

where L is the length of the device.

3.1. Graphene coated D-shaped single mode fiber

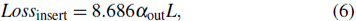
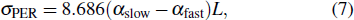
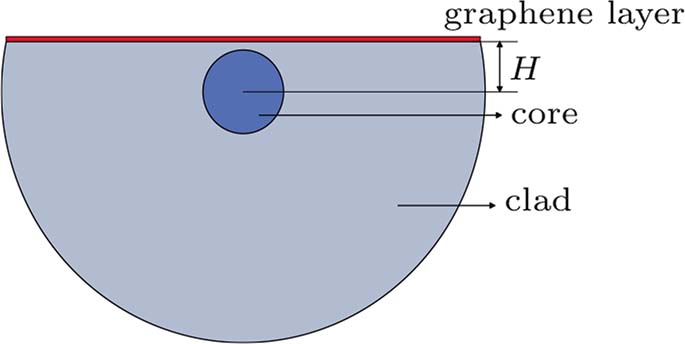
The cross-section of graphene-coated D-shaped single-mode fiber is shown in Fig. 1, in which the single-mode optical fiber is polished close to the core, the distance between the polishing surface and the core is H, and the graphene layer directly covers the polishing surface. The wavelength of the incident light in the simulation is set to be 1550 nm, the diameter of the core is set to be 9 μm, and the refractive indices of core and cladding are set to be 1.4609 and 1.4658, respectively. The polarizer-based graphene coated D-shaped single-mode fiber has been experimentally analyzed,[14] demonstrating the tunable polarizer modulation effect of the graphene coated polished fiber surface. In this paper, the transmission loss and polarization characteristics of D-fiber with graphene surface layers under the modulation of different electric fields are numerically analyzed for single-mode fiber and photonic crystal fiber. The graphene-coated single-mode optical fiber is used as a comparison of the light field transmission characteristics of the latter study.

Fig. 1. (color online) Cross-section of graphene coated D-shaped SMF.

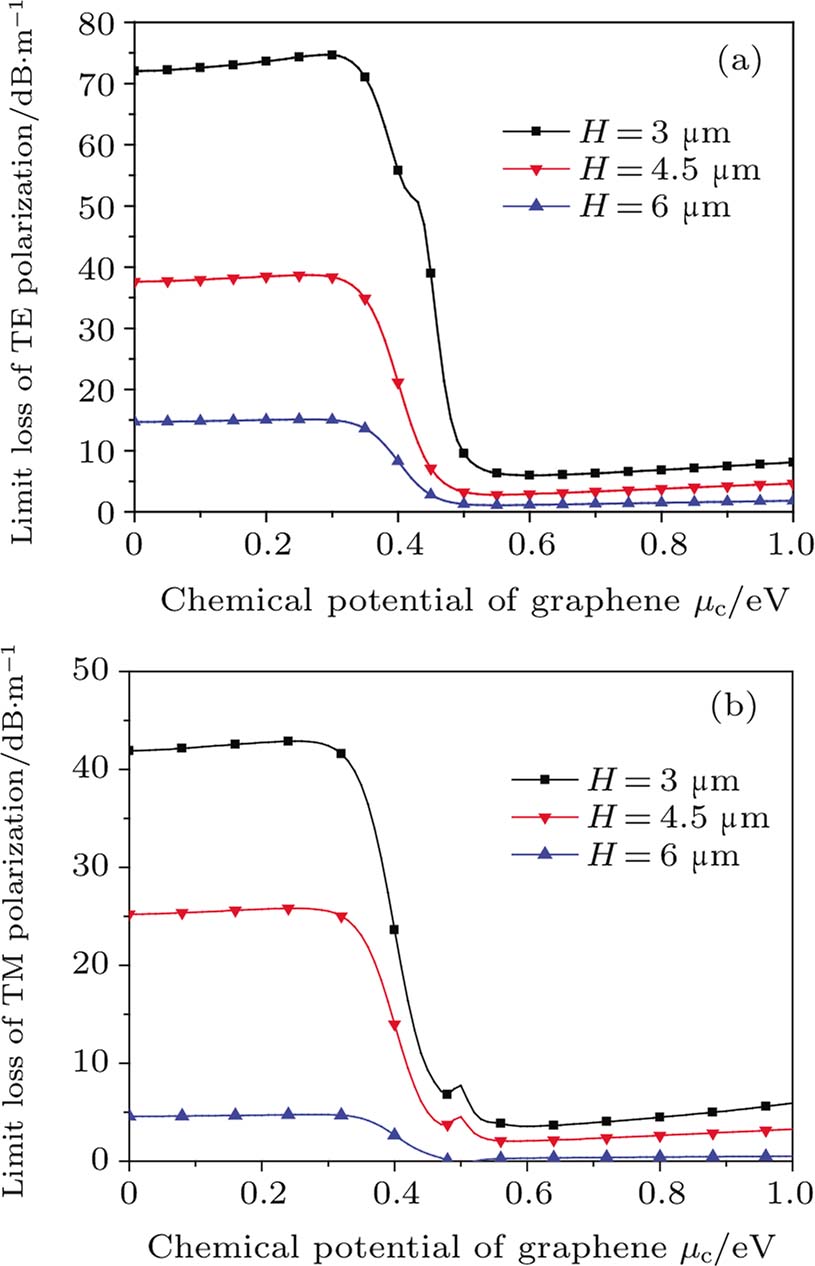The polishing depth of a single-mode fiber directly determines the distribution of the evanescent field of the fiber. First, the influence of different polishing depths on the light transmission with a single-layer of graphene coating is studied. Figure 2 shows different polarization mode loss characteristics with H of 6 μm (unpolished to the core), 4.5 μm (just to the edge of the core), and 3 μm (part of the core is polished), respectively.

Fig. 2. (color online) Limit loss characteristics of the monolayer graphene coated D-shaped SMF with different polishing depths. (a) TE mode loss. (b) TM mode loss.

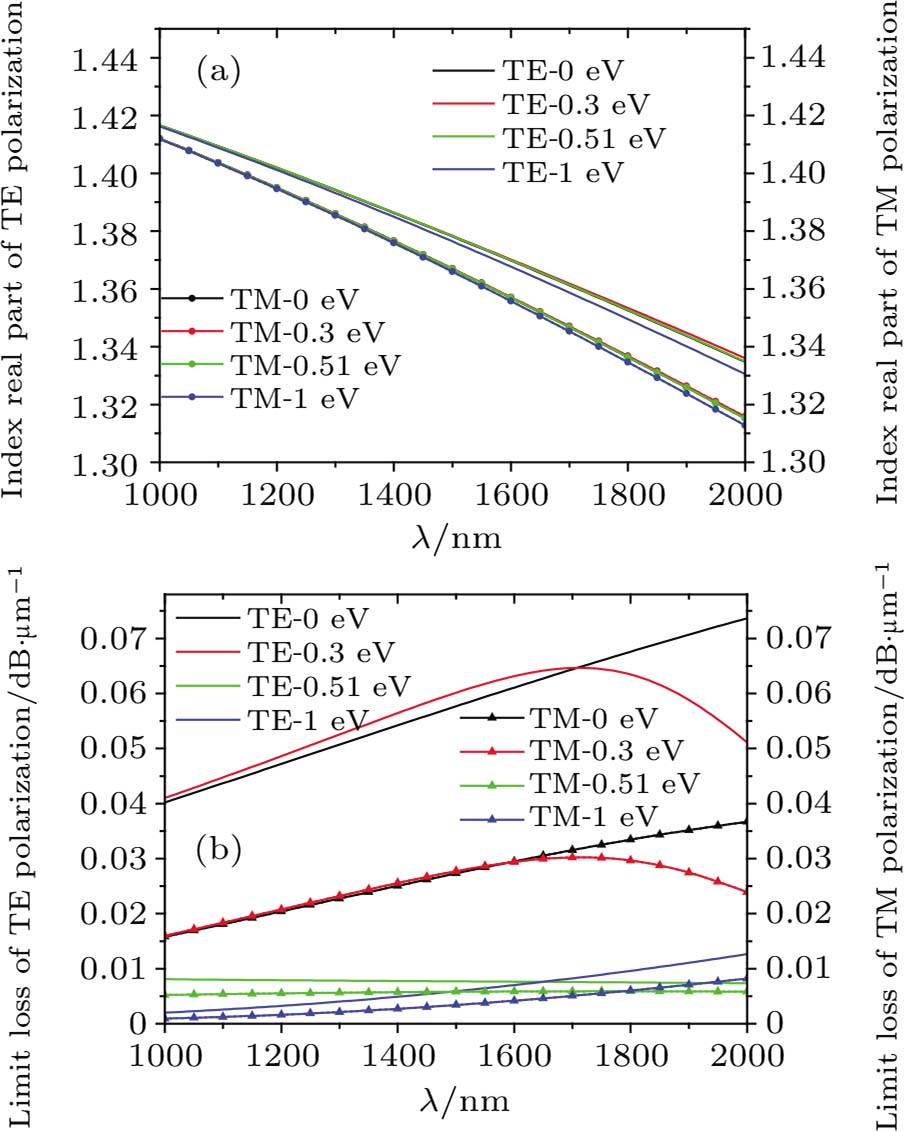
The limit loss increases with the polishing depth because there is more leakage of light, and the transmission loss of the TE mode is greater than that of the TM mode under the same polishing depth with a single-layer graphene coating due to more light absorption to the TE mode. In the TM mode, the peak of loss appears near the zero point (0.5 eV) of the dielectric constant and increases with the increase of the polish depth, but it is not confirmed in the TE mode. It is proved that graphene has played a role in fiber transmission. At H = 4.5 μm, for the TE mode, the maximum loss is 38.68 dB/m and the minimum loss is 2.8 dB/m, while for the TM mode, the maximum loss is 25.81 dB/m and the minimum loss is 2.06 dB/m. The real part of the effective refractive index has little change with the increase of the chemical potential under the same polishing depth and decreases with the increase of the polishing depth, as shown in Table 1.

Table 1.

Real part of the effective refractive index.

.
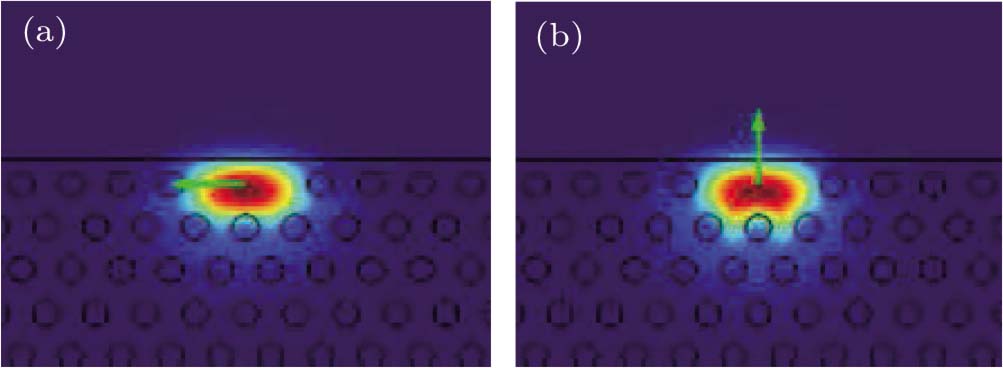
3.2. Characteristics of graphene-coated D-type photonic crystal fiber

With a flexible structure and independence on the temperature, photonic crystal fiber is being explored for more and more applications.[15,16] The cross-section of graphene coated D-shaped PCF is shown in Fig. 3. The photonic crystal fiber is of the total internal reflection type and has a six-ring air-hole structure, and graphene and a buffer layer are subsequently coated on the upper surface of the side polished fiber Λ is 1.5 μm, which is the hole space between the air holes. H is the distance from the polished surface to the fiber core, dair is the diameter of the air hole, dg is 0.34 nm, which is the thickness of monolayer graphene, and dh−BN (7 nm) is the thickness of buffer layer, which is hexagonal boron nitride.[17,18] Figure 4 shows the mode field distributions of TE and TM modes propagating in PCF without graphene coating, which demonstrates that the evanescent field is fundamental for the coupling between light and graphene.

Fig. 3. (color online) Cross-section of graphene covered D-type PCF.
Fig. 4. (color online) The D-PCF mode field distribution. (a) TE mode. (b) TM mode.

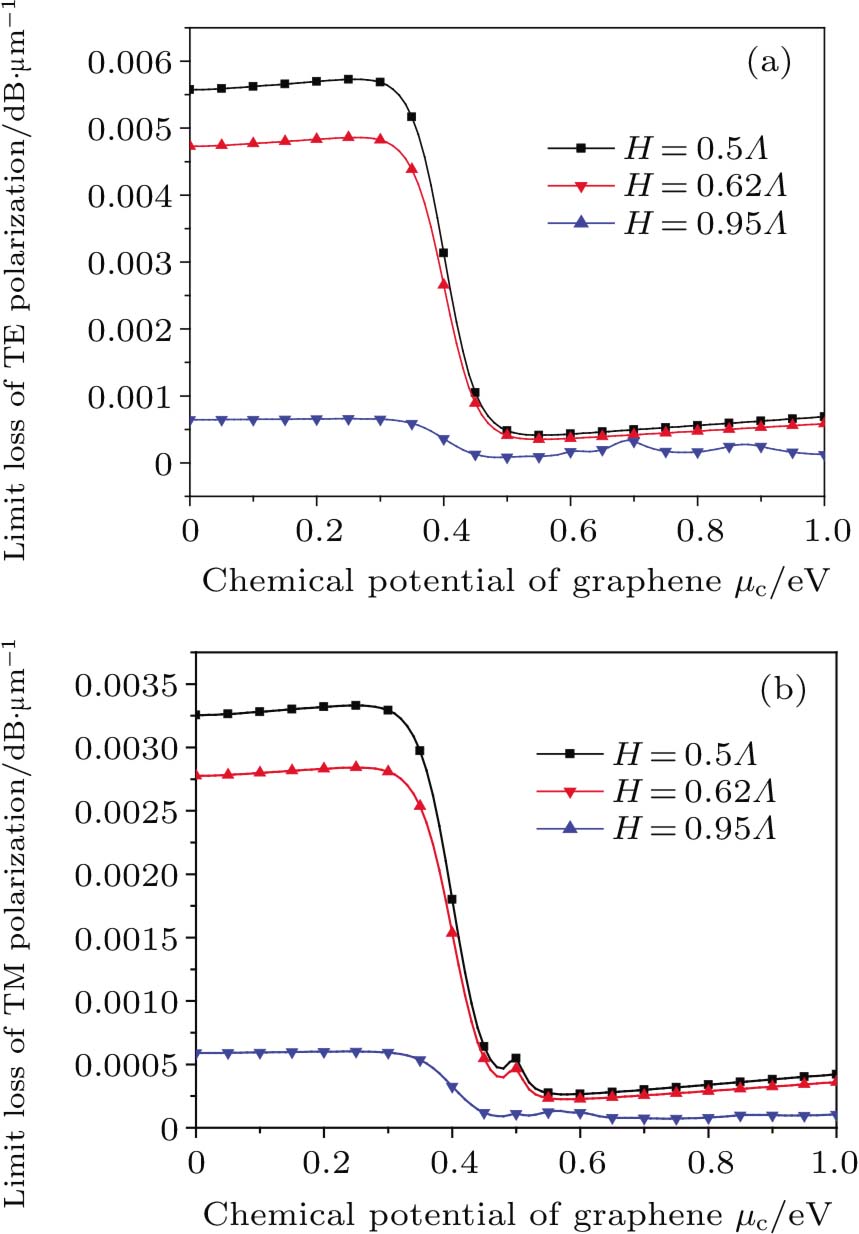The limit loss of the TE mode and TM mode as a function of polishing depth of H = 0.5Λ (just polished to the edge of the core), H = 0.62Λ (just part of the core section is polished), and H = 0.95Λ (core is not polished) is shown in Fig. 5. The limit loss increases with the polishing depth, an order of magnitude more than that of single-mode fiber. The strong constraint of light in the structure of photonic crystal fiber contributes to the enhancement in the interaction between light and graphene.

Fig. 5. (color online) Limit loss as a function of the chemical potential for D-PCF with different polishing depths of (a) TE mode and (b) TM mode.

Figure 6 shows the transmission loss as a function of the chemical potential of graphene, with different layers coated on D-shaped photonic crystal fiber (1–6 layers, buffer layers of 7 nm and graphene layer overlap each other), the same air-hole/space ratio of 0.5, and the polishing depth of 0.5Λ. When the chemical potential of graphene is less than 0.3 eV, the limit loss of the TE mode and TM mode is greater; while the chemical potential of graphene is larger than 0.56 eV, the limit loss becomes relatively small, which contributes to the refractive index of graphene modulated by the chemical potential. The transmission loss increases with the number of graphene layers. The light absorption of the graphene layer for different polarization directions results in a greater loss of TE polarization than that of TM polarization, which provides an exploration in the TM polarizer. Limit loss increases with the increase of graphene-light interaction.

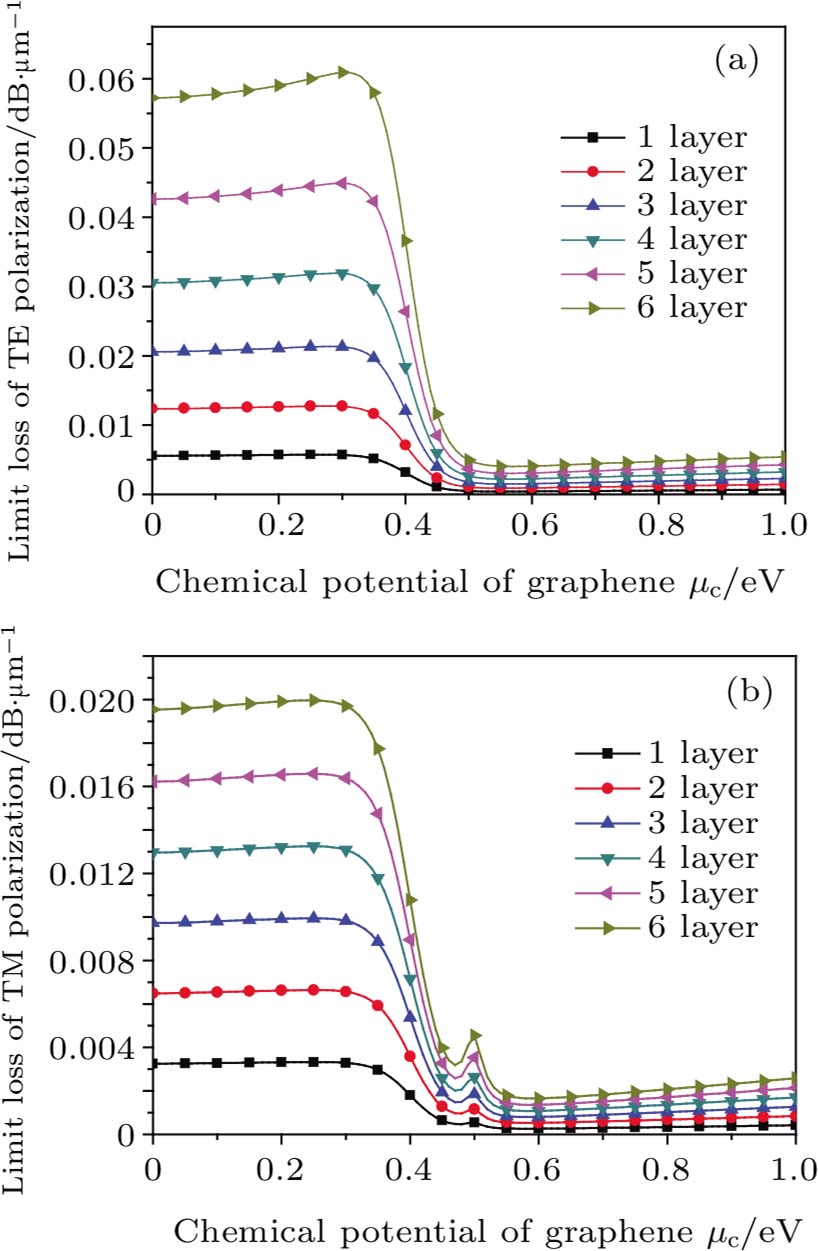Fig. 6. (color online) Limiting loss of graphene as a function of the chemical potential for PCF with different air hole layers for (a) TE mode and (b) TM mode.

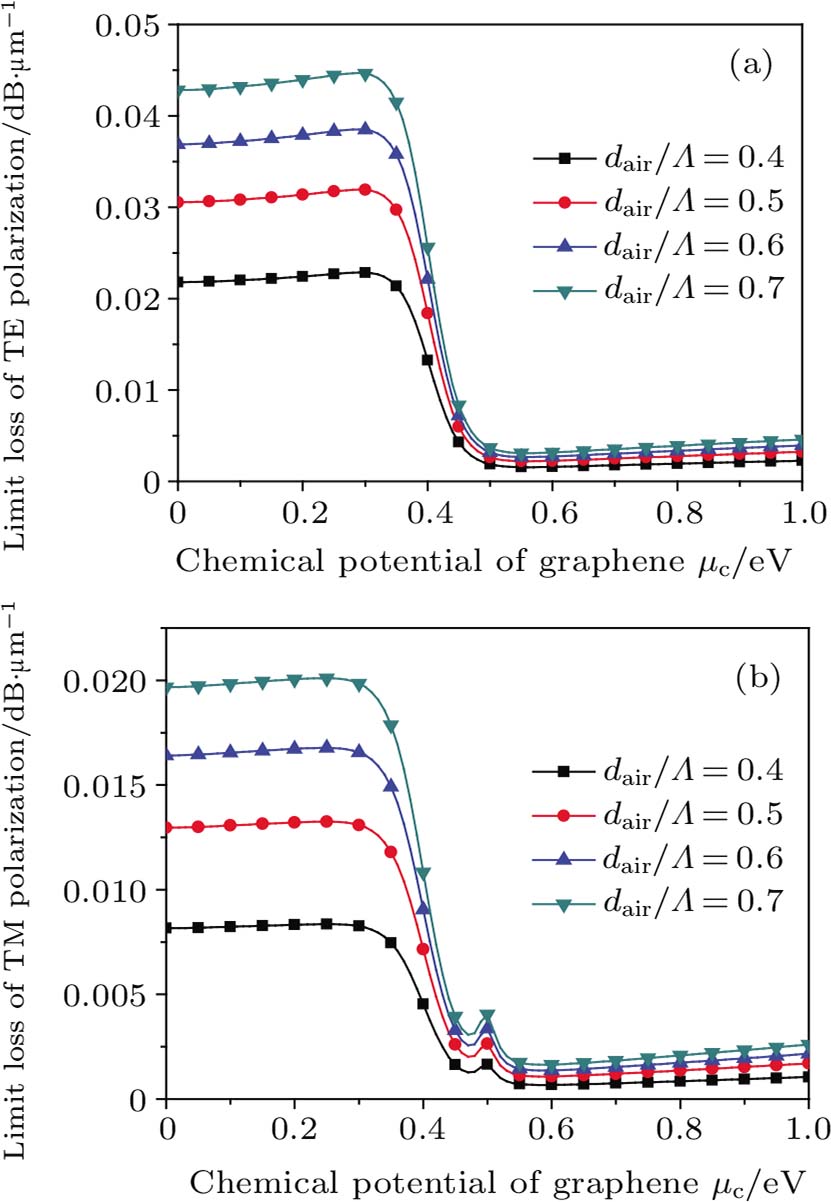When the polishing depth and the number of graphene layers are fixed, i.e., H = 0.5Λ and four layers, figure 7 shows that the structure of the photonic crystal fiber induces different transmission losses of TE and TM modes, and the larger the air hole/space ratio (from 0.4 to 0.7), the greater the transmission loss, which changes sharply from 0 to 0.4 eV and smoothly from 0.5 eV to 1 eV. The larger area of air in the fiber induces the enhancement in the constraint of light in the fiber core, resulting in more coupling between light and graphene and greater transmission loss. Larger loss changes in the turn-off area and smaller loss changes in the pass area are very conducive to the design of the polarizer.

Fig. 7. (color online) Limit loss as a function of the chemical potential for different structures of PCF for (a) TE mode and (b) TM mode.

Figure 8 shows the impact of different polishing depths on the transmission loss when the air hole/space ratio and the number of graphene layers are fixed. The polishing depth cannot be infinite due to the air hole structure in the photonic crystal fiber, and the numerical analysis is conducted when the polishing depths are 0.3Λ, 0.4Λ, 0.5Λ, and 0.6Λ. The transmission loss decreases with the reduction of the polishing depth, which is obviously contributing to the smaller interaction between light and graphene. The loss difference between TE and TM modes at a chemical potential of 0.3 eV is reduced, which is the best extinction ratio of the polarizer.

Fig. 8. (color online) (a) Limit loss with different polishing depths for TE mode and TM mode, and (b) the difference of limit loss between TE and TM modes as a function of the chemical potential.

It can be found that for the D-shaped PCF coated graphene layer structure, the more graphene layers there are, the greater the air hole/space ratio, the greater the polishing depth, and the more advantageous the polarizer design. However, the number of layers is limited by the insertion loss of the device. When the number of graphene layers is more than 10, the minimum value of loss is larger. When the number of graphene layers increases by 20, the buffer layer structure weakens the ability of the optical fiber to restrict light so much that the light cannot propagate inside the optical fiber core.

3.3. Polarizer model

From the numerical analysis, a polarizer based on graphene coated D-shaped photonic crystal fiber is designed. The structural parameters of graphene coated D-shaped photonic crystal fiber are that the polishing depth is H = 0.4Λ, and the air hole/space ratio is 0.8. The polarizer is a TM mode polarizer, since only the TM polarized light can pass through the polarizer in the “ON” status, when the difference between TE mode and TM mode is the largest. The loss difference at 0.3 eV achieves 0.03313 dB/μm, the minimum loss difference at 0.51 eV is 7 × 10−5 dB/μm, the polarization extinction ratio of this device achieves 66.26 dB/mm, and the insertion loss is 9.4 dB/mm. The device length is 70.31 μm < L < 151.64 μm decided by the transmission formula[19]Lmax = λ/(4π · Im(neff)), and the graphene chemical potentials at work status “on” and “off” are 0.3 eV and 0.51 eV, respectively.

If only the TM light is launched into the fiber, the device is a TM polarization modulator. The TM mode is turned off at a chemical potential of 0.25 eV with a transmission loss of 0.02902 dB/μm, and turned on at a chemical potential of 0.47 eV with a minimum transmission loss of 0.00445 dB/μm, and this TM modulator has an extinction ratio of 5 dB with a device length of 100 μm and an insertion loss of 0.9 dB. If only the TE light is launched into the fiber, the device is a TE polarization modulator. The TE mode is turned off at a chemical potential of 0.28 eV with a maximum transmission loss of 0.06186 dB/μm, and turned on at a chemical potential of 0.56 eV with a minimum transmission loss of 0.0043 dB/μm, and this TE modulator has an extinction ratio of 11.3 dB with a device length of 100 μm and an insertion loss of 0.86 dB.

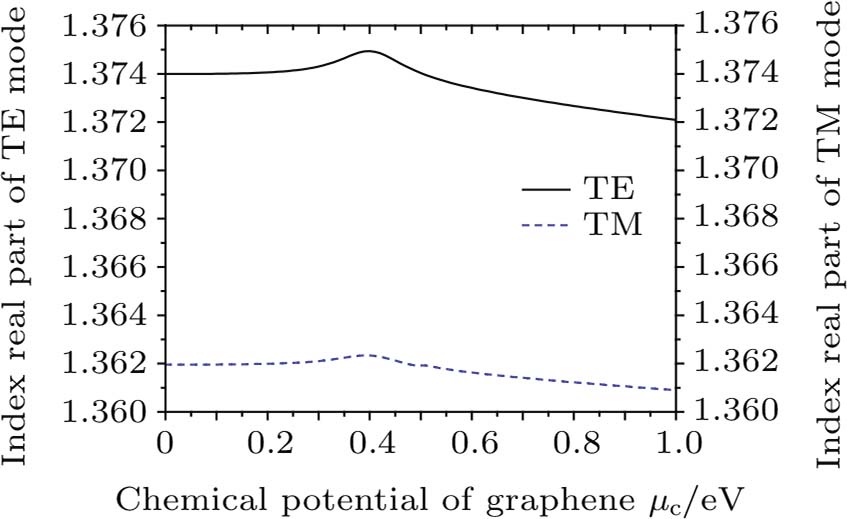
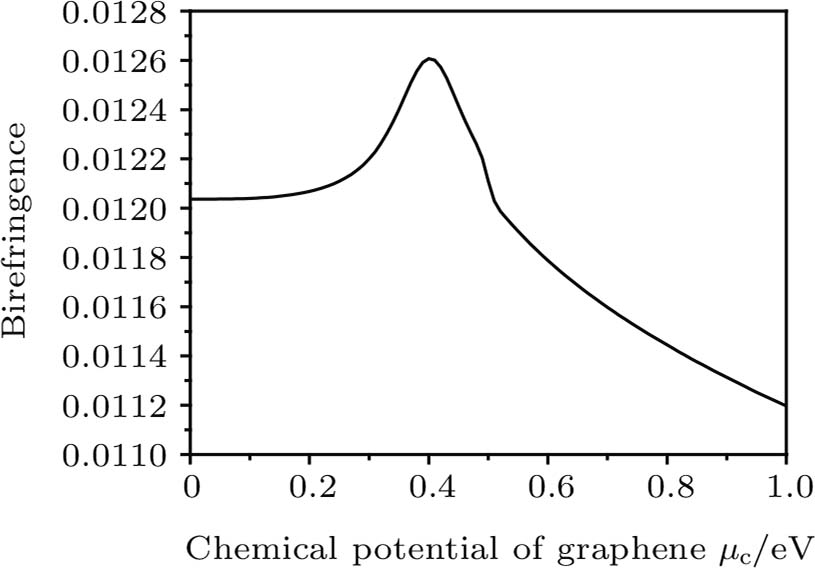
Figure 9 shows that the real part of the effective refractive index of TE mode and TM mode with the above structure, which first increases to a maximum at a chemical potential of 0.4 eV and then decreases, and the real part of the effective refractive index of the TE mode is larger than that of the TM mode. The maximum of the real part of the effective refractive index is decided by the chemical potential and the wavelength of the propagating light, which is the transition point between interband transition and intraband transition at the chemical potential ħω/2.

Fig. 9. (color online) The real part of the refractive index evaluates with the chemical potential.

The difference between the real part of the effective refractive index of the TE mode and TM mode generates a birefringence effect, which also first increases to the maximum and then decreases with the increase of the chemical potential, as shown in Fig. 10. The birefringence is up to 0.0126 at a corresponding chemical potential of 0.41 eV with a wavelength of 1550 nm, which is an order of magnitude higher than that in the reference.[20]

Fig. 10. Birefringence as a function of the chemical potential.

Figure 11 shows the refractive index of the fiber as a function of the incident wavelength with a polishing depth of H = 0.4Λ and an air-hole/space ratio of 0.8. It is found that the chemical potential has little effect on the real part of the effective refractive index. Instead, the real part of the effective refractive index decreases more sharply with the increase of the incident wavelength for the TE mode, while the limit loss becomes larger with the reduction of the chemical potential, and the limit loss of the TE mode is larger than that of the TM mode.

Fig. 11. (color online) Refractive index as a function of the incident wavelength. (a) The real part of the effective refractive index and (b) the limit loss evaluation with the incident wavelength.
4. Conclusion

In this paper, a polarizer based on graphene coated D-shaped photonic crystal fiber is proposed. From the numerical analysis of the impact of structural changes of the photonic crystal fiber geometry parameters, the number of the graphene layer, and the polishing depth on the TE mode and TM mode, the optimal polarizer model is demonstrated with an extinction ratio of 66.26 dB/mm, the insertion loss reaches 9.4 dB/mm when the polishing depth is H = 0.4Λ, the number of the graphene layer is four, and the air-hole/space ratio is 0.8. The TE mode modulator extinction ratio achieves 11.5 dB and the TM mode modulator extinction ratio is 5 dB when the device length is 100 μm.

Reference
[1] Zhou F Jin X F Hao R Zhang X M Chi H Zheng S L 2016 J. Opt. 45 337
[2] Zhang H J Healy N Shen L Huang C C Hewak D W Peacock A C 2016 Sci. Rep. 6 23512
[3] Bao Q Zhang H Wang Y Ni Z H Yan Y L Xiang Z Loh K P Tang D Y 2009 Adv. Funct. Mater. 19 3077
[4] He X Y Wang D N 2013 Proceedings of Asia Communications and Photonics Conference November 12–15, 2013 Beijing, China AW4C.6
[5] Zapata J D Saito L A M Cárdenas A M Thoroh De Souza E A 2016 CLEO: Applications and Technology June 5–10, 2016 San Jose, California, USA JTu5A.71
[6] Lin Y H Yang C Y Liou J H Yu C P Lin G R 2013 Opt. Express 21 16763
[7] Bi W H Wang Y Y Fu G W Li C L 2016 Acta Phys. Sin. 65 047801 in Chinese
[8] Geim A K Novoselov K S 2007 Nat. Mater. 60 183
[9] Hanson G W 2008 J. Appl. Phys. 103 064302
[10] Gosciniak J Tan D T 2013 Sci. Rep. 3 1897
[11] Mikhailov S A Ziegler K 2007 Phys. Rev. Lett. 99 016803
[12] Gong T R Yan F P Wang L Jian S S 2008 Chin. J. Lasers 35 559
[13] Chen H Z Liu W Wu Z C Wu W 2015 Piezoelectrics and Acoustooptics 37 228
[14] Bao Q Zhang H Wang B Ni Z H Lim C H Y X Wang Y Tang D Y Loh K P 2011 Nat. Photon. 5 411
[15] Wu X X Fan W D Liao W Y Tang W H Sui J N Cao X W Li Y G 2016 Acta Photonica Sin. 45 0106002
[16] Dash J N Jha R 2016 Opt. Quantum Electron. 48 1
[17] Ahn G Kim H R Ko T Y Choi K Watanabe K Taniguchi T Hong B H Ryu S 2013 ACS Nano 7 1533
[18] Tong L M Lou J Y Mazur E 2004 Opt. Express 12 1025
[19] Zhou F Jin X F Hao R Zhang X M Chi H Zheng S L 2016 J. Opt. 45 1
[20] Bi W H Li C L Wang X Y Fu G W Fu X H Yang K L Ma J Y 2016 Acta Opt. Sin. 36 1026013 in Chinese