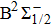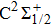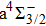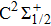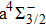Laser cooling of CH molecule: Insights from <em>ab initio</em> study

Cite this Article

Cui Jie, Xu Jian-Gang, Qi Jian-Xia, Dou Ge, Zhang Yun-Guang. Laser cooling of CH molecule: Insights from ab initio study. Chinese Physics B, 2018, 27(10): 103101 Copy to clipboard

Permissions

Laser cooling of CH molecule: Insights from ab initio study

Cui Jie, Xu Jian-Gang, Qi Jian-Xia, Dou Ge, Zhang Yun-Guang^†

School of Science, Xi’an University of Posts and Telecommunications, Xi’an 710121, China

† Corresponding author. E-mail: zygsr2010@163.com

Project supported by the National Natural Science Foundation of China (Grant No. 61705182).

Abstract

The feasibility of laser cooling a CH molecule is investigated theoretically by employing the ab initio method. The potential energy curves for the five Λ–S states and eight Ω states of CH are determined by the multi-reference configuration interaction with the Davidson corrections (MRCI+Q) level of theory. The results agree well with the available experimental data and other theoretical values. Also, the permanent dipole moments and transition dipole moments of the CH molecule are calculated at the multi-reference configuration interaction (MRCI) level. We find highly diagonally distributed Franck–Condon factors (f₀₀ = 0.9950 and 0.9998) and branching ratios (R₀₀ = 0.983 and 0.993) for the A²Δ → X²Π and C²Σ⁺ → X²Π transitions. Moreover, the values of suitable radiative lifetime τ of the A²Δ and C²Σ⁺ states are evaluated to be 9.64 × 10⁻⁷ s and 2.02 × 10⁻⁷ s, respectively, for rapid laser cooling. A scheme for laser cooling the CH molecule is designed. In the proposed cooling scheme, three wavelengths for A²Δ → X²Π and C²Σ⁺ → X²Π transitions are used, and the main pump lasers are λ₀₀ = 430.86 nm and 313.45 nm, respectively. The feasibility of laser cooling the CH molecules is demonstrated for each of these schemes, and this study offers a theoretical basis for experimental research into preparation of cold CH molecules.

PACS: 31.15.A-;37.10.Mn;87.80.Cc

Keyword:spectroscopic constants;transition diople moments;Franck-Condon factors;laser cooling

Show Figures

1. Introduction

The production of ultracold polar molecules can be useful in several emerging fields such as quantum simulation,^[1,2] chemical dynamics,^[3] and new platforms for quantum computing,^[4] as well as in controlling chemistry.^[5] Consequently, the interest in potential molecular candidates for laser cooling has grown in response to the commencement of investigation and experimental research in this field. As early as 2004, Di Rosa^[6] conducted a brief survey of candidate molecules for laser cooling and identified a series of hydrides and halides, including CaH, AlH, AlF, AlCl, etc. However, it was thought to be difficult to directly laser cool molecules because of their complex structures until the direct laser cooling of SrF molecules was first achieved and reported by Shuman et al. in 2010.^[7] Since then, successful laser cooling experiments have been performed for YO, CaF, BH, and BaH.^[8–12] Based on existing investigations, it can be concluded that molecular candidates for laser cooling must possess highly-diagonal Franck–Condon factors (FCFs) and short radiative lifetimes. In practice, highly-diagonal FCFs mean that a limited number of lasers is required to keep the molecule in a closed-loop cooling cycle, and short lifetimes can ensure high spontaneous emission.

Very recently, laser cooling of diatomic polar molecules and molecular ions has begun to attract the attention of researchers. In published research, it was predicted that some alkaline-earth-metal hydrides and halides, such as BeH, MgH, BeCl, could be laser-cooled.^[13–17] These molecules have one thing in common: they have no intervening state between the proposed transition for the laser cooling. Therefore, it is necessary to ensure that if an intervening state exists, there is nonetheless closed cycling between the upper state and the ground state of the transition. The A¹Π → X¹Σ⁺ and a³Π → X¹Σ⁺ transitions of AlF were studied by Wells and Lane,^[18] these two transitions both have highly diagonal FCFs, and the lifetimes are also extremely short. Fortunately, the emission rate of a³Π state is very small. Soon after this study, laser cooling of the SiO⁺ molecular ion was investigated by Nguyen and Odom^[19] who found that between B²Σ⁺ and X²Σ⁺ states, there exits an intervening state, A²Σ⁺, but, due to its short lifetime, this did not prohibit the possibility of laser cooling. Following the publication of this study, increasing numbers of reports^[20] of similar molecules, in which there exist intervening states, have provided bases for further research.

Here in this research, we report the accurate calculation of spectroscopic parameters and transition properties for the CH molecule to ensure its suitability for laser cooling. The CH radical occurring ubiquitously in interstellar space,^[21] and high-power laser photochemistry^[22] have been the subjects of numerous theoretical and experimental investigations. The experimental values of spin–orbit splitting for the X²Σ and A²Δ states of the CH molecule are 27.95 cm⁻¹ and 1.0 cm⁻¹, respectively, which were derived by Huber and Herzberg,^[23] in 1979. In recent years, the spectroscopic constants of the X²Σ and A²Δ states were calculated by using different theoretical methods.^[24–27] In 2003, Sun and Freed^[28] used an ab initio effective valence shell Hamiltonian method to carry out a theoretical investigation of the spin–orbit splitting, and their results for the energies of these two states are 33.96 cm⁻¹ and 1.27 cm⁻¹, respectively. In these previous theoretical and experimental studies,^{[24–27,29–34]} for the A²Δ → X²Σ transition, the region of transition energy (T_e) from the A²Δ state to the X²Σ state was between 23147.884 cm⁻¹ and 23565.4 cm⁻¹; for the C²Σ⁺ → X²Σ transition, the region of T_e was from 31802.128 cm⁻¹ to 32205.44 cm⁻¹. However, to the best of our knowledge, a systematic study of the laser cooling of CH is unavailable so far. The objective of the present work is to design a viable scheme to facilitate the laser cooling of the CH molecule, including computation of permanent dipole moments (PDMs), transition dipole moments (TDMs), FCFs, radiative lifetimes, and wavelengths for the A²Δ → X²Σ and C²Σ⁺ → X²Σ transitions of CH molecule by using a high-level ab initio method.

The rest of this paper is arranged as follows. In Section 2, we detail the ab initio method and basis sets chosen in the presented calculations of the electronic states of CH molecules. The results of the spectroscopic parameters obtained for the Λ–S and Ω states and laser cooling for the Λ–S states of CH are provided and discussed in Section 3. Finally, some conclusions are given in Section 4.

2. Computational details

By using the MOLPRO 2015 program package,^[35] all electronic structures of CH molecules for the X²Σ, a⁴Σ⁻, A²Δ, B²Σ⁻, and C²Σ⁺ states are calculated. In the first step we used the Post restricted Hartree–Fock (RHF) method to calculate the energy for the ground state. The next step was to obtain a multi-reference wavefunction by using the complete active space self-consistent-field (CASSCF) method.^[36–38] The final step was based on the zero-order function, by using the multi-reference configuration interaction (MRCI) plus Davidson corrections (MRCI+Q) to calculate energies for the CH molecule,^[39–42] and taking advantage of the Douglas–Kroll (DHK) method for correction.^[43–45] The spin–orbit coupling (SOC) effects were also taken into consideration in the MRCI+Q calculations of the CH molecule.

Due to the limitation of the summary of the MOLPRO program package, the computations were performed within the C_2v point group symmetry, which has four irreducible representations (irreps) (A₁, B₁, B₂, and A₂). The A₁ irrep yields the Σ⁺ state and a component of Δ states, B₁ provides the Π state, and A₂ yields the Σ⁻ state and the other components of Δ states. In the CASSCF calculations, six molecule orbitals are chosen as the active space, including four A₁, one B₁, and one B₂. Five electrons are distributed in the (4110) active space. The aug-cc-pV5Z basis set is chosen for the hydrogen atom, and the aug-cc-pCV5Z basis set is for the carbon atom. In all electronic structure calculations, the aug-cc-pCV5Z (ACV5Z) basis set is used for the Λ–S and Ω states.

For the bound Λ–S and Ω states, all potential energy curves (PECs) are calculated with an interval of 0.05 nm over the distance of 0.04 nm–1.5 nm. To achieve the accurate results, the interval value is reduced to 0.02 nm, nearly the equilibrium bond distance. The spectroscopic constants are calculated by solving the nuclear Schrödinger equation through using the LEVEL 8.2 program, including the equilibrium bond length, R_e, harmonic and an harmonic vibrational constants, ω_e and ω_e χ_e, respectively, rotational constant, B_e, and adiabatic relative electronic energy referred to the ground state, T_e.^[46] With the PECs and TDMs of the different electronic states, this program can also yield the FCFs and Einstein coefficients for all possible discrete transitions allowed by selection rules. The Einstein coefficient A_v′v for the rate of spontaneous emission from an initial rovibrational level (v, J) into the final rovibrational level (v′, J′) is defined by the expression^[47]

where M(r) is the function of transition dipole in units of D, v is the emission frequency, ψ_v′J′ and ψ_vJ are the normalized radial wavefunctions, the energy difference ΔE_v′v is in units of cm⁻¹, and S(J′, J) is the Hönl–London rotational intensity factor.^[48,49] Using the Einstein coefficient for spontaneous emission, the radiative lifetime can be calculated from the following formula:

3. Results and discussion

3.1. PECs and spectroscopic constants of Λ–S states

To determine whether the CH molecule is suitable for laser cooling, we must calculate the PECs and spectroscopic constants. At the MRCI+Q level, the CH molecule for the lowest two dissociation channels, C(³P) + H(²S) and C(¹D) + H(²S), and the X²Σ, a⁴Σ⁻, A²Δ, B²Σ⁻, and C²Σ⁺ states are obtained. Figure 1 shows the PECs for the Λ–S states of the CH molecule. The associated sets of calculated spectroscopic parameters with available experimental data^[29–34] and theoretical results^[24–27] of CH are summarized in Table 1 for comparison.

	Figure Option View Download New Window
	Fig. 1. (color online) PECs for the five Λ–S states of CH molecule.

Table 1.

Spectroscopic constants for Λ–S states of CH molecule at MRCI+Q level.

As for the ground state X²Σ, the equilibrium bond distance and the vibrational frequency are calculated to be R_e = 1.1181 Å and ω_e = 2859.4759 cm⁻¹, and their corresponding differences from experimental values are only 0.0019 Å and 1.3241 cm⁻¹, respectively:^[29,30] the percentage errors are only 0.17% and 0.05%, respectively. Compared with other theoretical values^[24–27] of ω_e χ_e and B_e, our constants ω_e χ_e = 62.3206 cm⁻¹ and B_e = 14.5084 cm⁻¹ are in good accordance with the experimental data of 64.4 cm⁻¹ and 14.457 cm⁻¹. Our computed value for D_e is 3.669 eV, while the experimental value is 3.472 eV, and the percentage error is 5.67%. For the second singlet excited state B²Σ⁻, in the case of the spectroscopic constants R_e, and T_e, our data, 1.1624 Å, 26007.57 cm⁻¹, respectively, are in better agreement with the experimental data (1.164 Å, 26059.517 cm⁻¹) than those of other published calculations.^[32,33] The value of ω_e that we computed for the B²Σ⁻ state is larger than the experimental measurement, giving a percentage error of 20.67%, but is in good agreement with other theoretical values, and the corresponding percentage error, between our theoretical value and others in the literature, for the B²Σ⁻ state is 0.05% (Ref. [24]) ≤ δ ω_e/ω_e ≤ 1.85% (Ref. [25]).

For the first singlet excited state A²Δ of the higher dissociation channel C(¹D) + H(²S), shown in Fig. 1, the calculated T_e from the X²Σ state is located at 23280.16 cm⁻¹. Our result of ω_e = 2967.2279 cm⁻¹ is a little overestimated with respect to the experimental and other theoretical results, the percentage error is 1.36% (Ref. [26]) ≤ δ ω_e/ω_e ≤ 2.71% (Ref. [25]). Our value of R_e is 1.1032 Å which is 0.0002 Å larger than the experimental value. The value of T_e from experiments^[30,31] is 23147.884 cm⁻¹, in other theoretical results it is 23395.072 cm⁻¹,^[24] 23510.830 cm⁻¹,^[25] 23565.4 cm⁻¹,^[26] as reported by Kalemos et al., Kleinschmidt et al., and Hettema and Yarkony, respectively. Obviously, our value of T_e is much closer to the experimental value than the other theoretical ones, the corresponding error relative to the experimental value is only 0.57%. For the third excited singlet C²Σ⁺ state, our values of R_e, ω_e χ_e, B_e, and T_e are much closer to the experimental data than theoretical ones reported by Richards et al.^[29] and Herzberg et al.^[34] Specifically, the differences between the experimental value and our value are only 0.0015 Å for R_e and 0.023 cm⁻¹ for B_e, respectively. We also notice that the error for the present result of C²Σ⁺ is a little larger than the experimental data. For example, our results for R_e, ω_e χ_e, B_e are 1.1155 Å, 128.2555 cm⁻¹, and 14.626 cm⁻¹, and the experimental values are 1.114 Å, 126 cm⁻¹, and 14.603 cm⁻¹, respectively. Obviously, the differences are very small; the percentage errors are 0.13%, 1.79%, and 0.16%, respectively. Concerning the quartet state, both previous studies and our present one obtain spectroscopic parameters for the a⁴Σ⁻state of the CH molecule. Compared with the theoretical data,^[24–27] our results for the a⁴Σ⁻ state are in good agreement. For instance, our value of ω_e = 3200.5941 cm⁻¹ is a little larger than the theoretical values in the literature, with a percentage error being 2.67%–3.74% for this difference; our result of R_e is 1.0872 Å, and the percentage error for this value is 0.26% (Ref. [24]) ≤ δR_e/R_e ≤ 0.53% (Ref. [25]).

In conclusion, our spectroscopic parameter results agree with those of the experimental data and theoretical results in terms of the X²Σ, a⁴Σ⁻, A²Δ, B²Σ⁻, and C²Σ⁺ states of CH.

3.2. PECs and spectroscopic constants of Ω states

For the CH molecule, the spin–orbit coupling (SOC) effect makes the five Λ–S states split into eight Ω states, i.e. four Ω = 1/2 states, three Ω = 3/2 states, and one Ω = 5/2 state. Four new dissociation limits,C(³P₀) + H(²S_1/2),C(³P₁) + H(²S_1/2), C(³P₂) + H(²S_1/2), and C(¹D₂) + H(²S_1/2) are generated from the original C(³P) + H(²S) and C(¹D) + H(²S) limits. 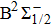The PECs for X²Σ_1/2, X²Σ_3/2, , , A²Δ_3/2, A²Δ_5/2, , and 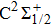states are plotted in Fig. 2, and the corresponding spectroscopic parameters for the eight Ω states are listed in Table 2.

	Figure Option View Download New Window
	Fig. 2. (color online) PECs for eight Ω states for the CH molecule.

Table 2.

Spectroscopic constants of various bound Ω states of CH molecule.

As we can see from Table 2, the effects of SOC are weak on the spectroscopic constants for X²Σ, a⁴Σ⁻, B²Σ⁻, and C²Σ⁺ states, but the effect of SOC is great for the A²Δ state. For the state, the spectroscopic parameters are in excellent agreement with the corresponding values without considering the SOC effect; the differences are only 0.8286 cm⁻¹ and 0.1496 cm⁻¹ for ω_e and B_e, respectively. Our calculated spectroscopic parameters for the state are R_e = 1.1141 Å, ω_e = 2858.6584 cm⁻¹, ω_e χ_e = 121.0729 cm⁻¹, B_e = 14.6380 cm⁻¹, and T_e = 31961.73 cm⁻¹, which differ from the corresponding values computed without considering the SOC effect by only 0.001 Å, 8.5189 cm⁻¹, 7.1826 cm⁻¹, and 0.24 cm⁻¹, respectively.

Owing to the SOC effect, the Λ–S X²Σ state splits into two X²Σ_1/2 and X²Σ_3/2 states. For the two Ω states, the energy sequence from low to high is 1/2, 3/2, and the small difference of T_e between the states is 26.81 cm⁻¹. By comparing the X²Σ state and the X²Σ_1/2, X²Σ_3/2 states in Table 1 and Table 2, it can be seen that the spectroscopic parameters of the states X²Σ_1/2 and X²Σ_3/2 are similar to those of the X²Σ state. For example, the differences between the values of ω_e in the Ω states of X²Σ_1/2 and X²Σ_3/2 and that of the X²Σ state are only 3.0881 cm⁻¹ and 2.8474 cm⁻¹. The values of ω_e χ_e for the X²Σ_1/2 and X²Σ_3/2 states are only 0.7577 cm⁻¹ and 0.7456 cm⁻¹ smaller than the value for the X²Σ state, respectively. For the a⁴Σ⁻ state, which splits into two Ω states (, ), the spectroscopic data for the two Ω states are almost the same as the constants of the Λ–S state, and the difference in T_e between the two Ω states is 0.04 cm⁻¹. As for ω_e χ_e and B_e of the two Ω states, the largest differences of the a⁴Σ⁻ state are 0.3602 cm⁻¹ and 0.0013 cm⁻¹, respectively. The difference in T_e between A²Δ_3/2 and A²Δ_5/2 is 2.91 cm⁻¹. However, we also notice that the SOC effect is very large for the A²Δ state. As Table 2 shows, the two Ω states have the values of both ω_e and ω_e χ_e, which are quite different, the percentage differences are 5% and 21%, respectively. In addition, between these two Ω states, the difference in T_e is 2.91 cm⁻¹.

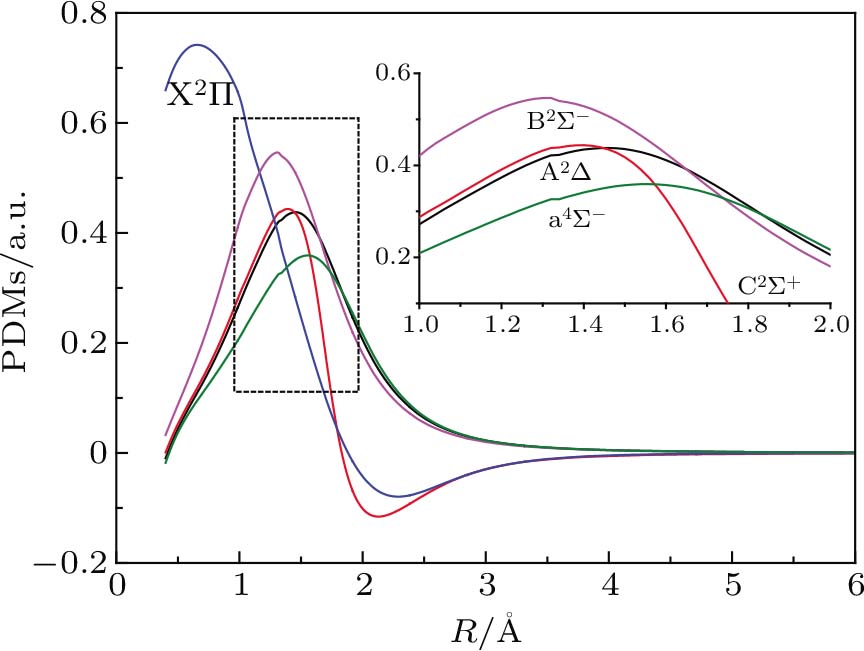
3.3. PDMs and TDMs

PDMs for the X²Σ, a⁴Σ⁻, A²Δ, B²Σ⁻, and C²Σ⁺ states are plotted in Fig. 3. As we can see from Fig. 3, the maximum PDM exhibited by the X²Σ state is much larger than the others, which is due to the deepest potential well of the ground state. For the ground state, the value reaches a maximum of about 0.7421 a.u. (the unit a.u. is short for atomic unit), and then drops to a minimum at 2.28 Å. Furthermore, the PDMs increase linearly up to approximately 2.34 Å. As for the C²Σ⁺ state, a maximum and a minimum also exist of the PDM at 1.4 Å and 2.12 Å, respectively. It can be clearly seen from Fig. 3 that the PDMs for the a⁴Σ⁻, A²Δ, and B²Σ⁻ states each have a similar trend, their maximum values being 0.3591, 0.4379, and 0.5466 a.u., respectively. Then, the PDMs of these states then all drop to zero when moving to approximately 4.8 Å. The PDM functions of the X²Σ, a⁴Σ⁻, A²Δ, B²Σ⁻, and C²Σ⁺ states at R_e are 0.4981, 0.2408, 0.2825, 0.5089, and 0.3505 a.u., respectively.

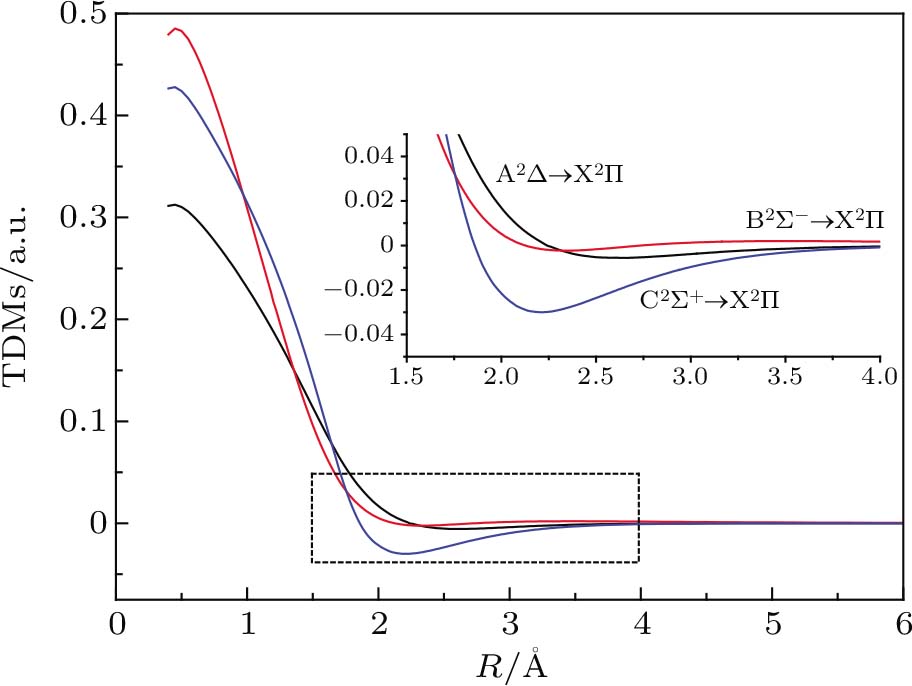
	Figure Option View Download New Window
	Fig. 3. (color online) PDMs for five Λ–S states of CH molecule.

The TDMs for the A²Δ → X²Σ, B²Σ⁻ → X²Σ, and C²Σ⁺ → X²Σ transitions as a function of the internuclear distance at the MRCI+Q level for the CH molecule are plotted in Fig. 4. There are intermediate states in A²Δ → X²Σ and C²Σ⁺ → X²Σ transitions. So it is necessary to study the influence of the intermediate state. For A²Δ → X²Σ, the intermediate state a⁴Σ⁻ has no effect on the transition, because the A²Δ → a⁴Σ⁻ transition is spin–orbit forbidden. Between the X²Π and C²Σ⁺, the intermediate states are a⁴Σ⁻, A²Δ, and B²Σ⁻. However, the transition of C²Σ⁺ → a⁴Σ⁻ is spin–orbit forbidden. The TDMs for C²Σ⁺ → A²Δ transition are about zero due to being orbit-forbidden and for the C²Σ⁺ → B²Σ⁻ transition they are about zero because the Σ⁺ → Σ⁻ is forbidden, which shows that the two transitions are unfeasible. So neither the a⁴Σ⁻ nor A²Δ, nor B²Σ⁻ has an effect on the C²Σ⁺ → X²Σ. Figure 4 shows that the TDMs for these three transitions fall to minima, after which these transitions rise, approaching zero with bond length increasing. In addition, the minimum of C²Σ⁺ → X²Σ transition is −0.03 Å, which is smaller than the other two transitions. The TDMs for the A²Δ, B²Σ⁻, and C²Σ⁺ states at R_e are 0.2102, 0.2364, and 0.2803 a.u., respectively. TDMs of the states are related to the Einstein coefficients and radiative lifetimes.

	Figure Option View Download New Window
	Fig. 4. (color online) TDMs for A²Δ → X²Σ, B²Σ⁻→ X²Σ, and C²Σ⁺ → X²Σ transitions of CH molecule.

3.4. Laser cooling of CH

As mentioned in Section 1, one of the criteria for laser cooling is that the molecule must possess highly diagonal FCFs, which can be used to describe the transition by the degree of overlap of the vibrational wave functions. The splitting constants for X²Σ and A²Δ are small for CH, i.e. A^SO(X²Σ_1/2 and X²Σ_3/2) = 26.81 cm⁻¹, A^SO(A²Δ_1/2 and A²Δ_3/2) = 2.91 cm⁻¹. So the SOC effect for laser cooling the CH molecule can be ignored. The influences of intermediate states are also considered. Fortunately, these intermediate states have no effect on the A²Δ → X²Σ transition nor on the C²Σ⁺ → X²Σ transition as mentioned in the TDM part. Here, the possibility of laser cooling on the A²Δ → X²Σ transition and C²Σ⁺ → X²Σ transition are considered. As can be seen in Table 3, the diagonal FCFs are f₀₀ = 0.9950 for the A²Δ → X²Σ transition and f₀₀ = 0.9998 for the C²Σ⁺ → X²Σ transition, which can greatly limit the number of lasers required to keep the molecule in a closed-loop cooling cycle. Other calculated diagonal FCFs for A²Δ → X²Σ such as f₁₁ (0.989), f₂₂ (0.991), f₃₃ (0.991), and for the C²Σ⁺ → X²Σ transition like f₁₁ (0.997), f₂₂ (0.970), f₃₃ (0.777) are smaller than f₀₀ but remain considerably large compared with the small off-diagonal terms. In addition, to demonstrate the distributions of FCFs for the different vibrational states of A²Δ → X²Σ and C²Σ⁺ → X²Σ transitions, all possible transitions between 0 ≤ v ≤ 3 and 0 ≤ v′ ≤ 1 are displayed in Table 3. Besides the large diagonal FCFs, another critical criterion for laser cooling a molecule is a suitable rate of optical cycling. This means that for the rapid laser cooling implementation, short spontaneous radiative lifetimes τ (10⁻⁸ s– 10⁻⁵ s) are required. The values of corresponding computed spontaneous radiative lifetime τ are collected in Table 3. As illustrated in the table, the values of spontaneous radiative lifetime τ of the A²Δ → X²Σ and C²Σ⁺ → X²Σ transitions are 9.64 × 10⁻⁷ s and 2.02 × 10⁻⁷ s, respectively, which are suitable for laser cooling the CH molecule.

Table 3.

Calculated values of FCF f_v′v, wavelength λ_v′v, and spontaneous radiative lifetime τ.

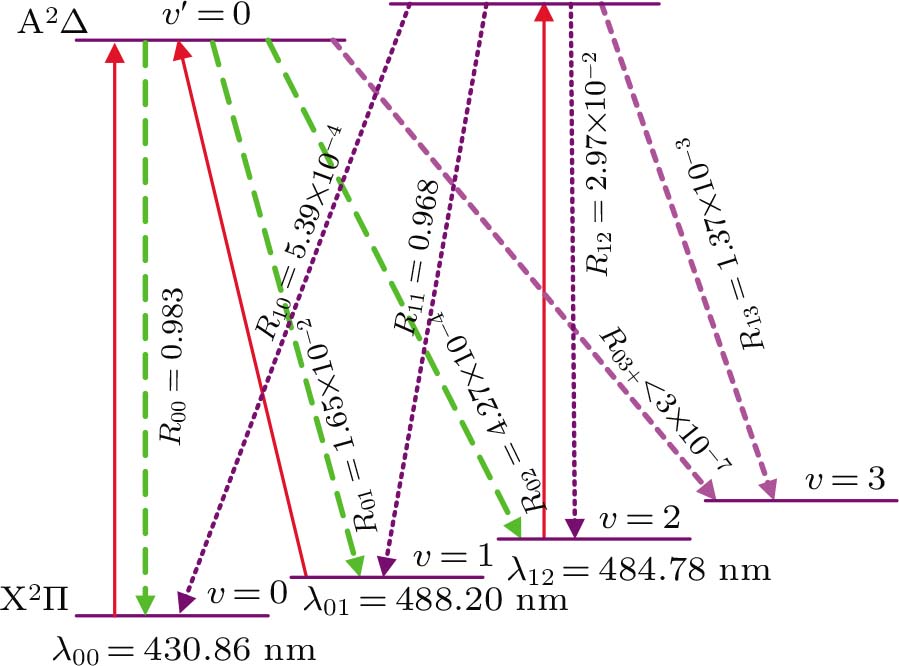
Comparing the relevant FCFs is a simple method of determining the cooling cycle, but it is not sufficient alone. The reason is that the relation between the relative strengths of the vibrational branching ratios and that between photon loss pathways are more direct than FCFs in the cooling cycle.^[50–52] Thus, the cooling cycle with branching ratio R_v′v, which can be calculated by using the ratio of Einstein coefficients A_v′v for each vibronic transition, is expressed as R_v′v = A_v′v/Σ_vA_v′v. The calculated values of Einstein coefficient A_v′v and vibrational branching ratio R_v′v of the A²Δ → X²Σ and C²Σ⁺ → X²Σ transitions are listed in Table 4. For the A²Δ → X²Σ transition, branching ratios of the diagonal terms R₀₀ = 0.983 and R₁₁ = 0.968 are obtained; branching ratios of the off-diagonal terms R₀₁ = 1.65 × 10⁻², R₀₂ = 4.27 × 10⁻⁴, R₀₃ = 1.05 × 10⁻⁵, R₁₀ = 5.39 × 10⁻⁴, R₁₂ = 2.97 × 10⁻², and R₁₃ = 1.37 × 10⁻³ are also calculated. The branching ratios to the v ⩾ 3 states of the CH molecule for the A²Δ → X²Σ transition are R₀₃₊ ≤3 × 10⁻⁷, so a cyclic system with three lasers involving v = 0, 1, 2, 3 of the X²Σ state and v′ = 0 and 1 levels of the A²Δ state is proposed, based on the calculated R_v′v. For the C²Σ⁺ → X²Σ transition, the diagonal terms R₀₀ (0.993) and R₁₁ (0.979) are a little smaller than f₀₀ (0.999) and f₁₁ (0.997). The value of R₀₃ is 3.73 × 10⁻⁶, which is larger than f₀₃ (4.04 × 10⁻⁷). However, the value of R₀₃ is small enough to make the C²Σ⁺ → X²Σ transition used as a quasi-cycling transition.

Table 4.

Calculated values of Einstein coefficient A_v′v and vibrational branching ratio R_v′v of A²Δ → X²Σ and C²Σ⁺ → X²Π transitions.

In Figs. 5 and 6, the two schemes show the arranged laser-driven transitions (solid red) and spontaneous decay (dotted line) for CH. As can be seen, the A²Δ (v′ = 0)→ X²Σ (v = 0) or C²Σ⁺ (v′ = 0)→ X²Σ (v = 0) transitions are the main pumps for cooling the CH molecule, requiring a laser with wavelength λ₀₀ = 430.86 nm or λ₀₀ = 313.45 nm, respectively. To augment the cooling effect, two cycles are added with A²Δ (v′ = 0)→ X²Π(v = 1) and C²Σ⁺ (v′ = 0)→ X²Σ (v = 1) transitions, which are the first vibrational pump, and the A²Δ (v′ = 1) → X²Π(v = 2) and C²Σ⁺ (v′ = 1) → X²Σ (v = 2) transitions are the second vibrational pump. Furthermore, the wavelengths of the two additional lasers for the A²Δ → X²Σ transition are λ₀₁ = 488.20 nm and λ₁₂ = 484.78 nm; for the C²Σ⁺ → X²Σ transition their wavelengths are λ₀₁ = 342.73 nm and λ₁₂ = 342.61 nm.

	Figure Option View Download New Window
	Fig. 5. (color online) Proposed laser cooling scheme for CH using A²Δ (v′)→ X²Π(v) transition (solid red) and spontaneous decay (dotted line) with calculated values of R_v′v. Here λ_v′v is the wavelength of A²Δ (v′) → X²Π(v) transition.

	Figure Option View Download New Window
	Fig. 6. (color online) Proposed laser cooling scheme for CH using the C²Σ⁺ (v′) → X²Π(v) transition (solid red) and spontaneous decay (dotted line) with calculated values of R_v′v. Here A_v′v is the wavelength of the C²Σ⁺ (v′) → X²Π(v) transition.

4. Conclusions

The PECs for the Λ–S states X²Σ, a⁴Σ⁻, A²Δ, B²Σ⁻, and C²Σ⁺, and the Ω states X²Σ_1/2, X²Σ_3/2, , , 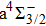A²Δ_3/2, A²Δ_5/2, , and 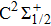of the CH molecule have been investigated at the MRCI+Q level with the aug-cc-pCV5Z basis set. Using the Level 8.2 program to solve the nuclear Schrödinger equation, the results of spectroscopic constants for these Λ–S and Ω states are obtained. Furthermore, the results agree well with previous experimental and other theoretical values.

In Subsection 3.3, our computed PDMs, for the X²Σ, a⁴Σ⁻, A²Δ, B²Σ⁻, and C²Σ⁺ states, and TDMs, for the spin-allowed transitions A²Δ → X²Σ, B²Σ⁻→ X²Σ, and C²Σ⁺ → X²Σ, are discussed. Based on PECs and TDMs that we obtained, the FCFs are calculated. The results indicate that the A²Δ → X²Σ and C²Σ⁺ → X²Σ transitions have highly diagonal FCFs (f₀₀ = 0.9950 and 0.9998) and branching ratios (R₀₀ = 0.983 and 0.993). Suitable radiative lifetimes, τ = 9.64 × 10⁻⁷ s for the A²Δ → X²Σ transition and τ = 2.02 × 10⁻⁷ s for the C²Σ⁺ → X²Σ transition, for ensuring the rapid and efficient laser cooling of the CH molecule are also obtained. The a⁴Σ⁻→ X²Σ transition is prohibitive to laser cooling because it is forbidden by selection rules. An optical scheme consisting of three laser cycles with the A²Δ → X²Σ and C²Σ⁺ → X²Σ transitions to create ultra cold CH molecules is proposed. The main cycling laser wavelengths for the A²Δ (v′ = 0)→ X²Π(v = 0) and C²Σ⁺ (v′ = 0)→ X²Π(v = 0) transitions are λ₀₀ = 430.86 nm and 313.45 nm, respectively. To enhance the cooling effect, two additional lasers with λ₁₀ = 488.20 nm and λ₂₁ = 484.78 nm are required for the A²Δ (v′ = 0)→ X²Π(v = 1) and A²Δ (v′ = 1) → X²Π(v = 2) transitions and λ₁₀ = 342.73 nm, λ₂₁ = 324.61 nm for C²Σ⁺ (v′ = 0)→ X²Π(v = 1), C²Σ⁺ (v′ = 1)→ X²Π(v = 2) transitions, respectively. The results indicate that laser cooling of the CH molecule is viable, and a reliable theoretical reference is provided for further theoretical and experimental research.

Reference

[1]	Ospelkaus S Ni K K Wang D de M H G Neyenhuis B QuéQner G Julienne P S Bohn J L Jin D S Ye J 2010 Science 327 853
[2]	Krems R V 2008 Phys. Chem. Chem. Phys. 10 4079
[3]	Baron J Campbell W C Demille D Doyle J M Gabrielse G Gurevich Y V Hess P W Hutzler N R Kirilov E Kozyryev I O’Leary B R Panda C D Parsons M F Petrik E S Spaun B Vutha A C West A D 2014 Science 343 269
[4]	Demille D 2002 Phys. Rev. Lett. 88 067901
[5]	Krems R V 2008 Phys. Chem. Chem. Phys. 10 4079
[6]	Rosa M D D 2004 Eur. Phys. J. 31 395
[7]	Shuman E S Barry J F Demille D 2010 Nature 467 820
[8]	Hummon M T Yeo M Stuhl B K Collopy A L Xia Y Ye J 2013 Phys. Rev. Lett. 110 143001
[9]	Zhelyazkova V Cournol A Wall T E Matsushima A Hudson J J Hinds E A Tarbutt M R Sauer B E 2014 Phys. Rev. 89 12707
[10]	Hendricks R J Holl D A Truppe S Sauer B E Tarbutt M R 2014 Front. Phys. 2 51
[11]	Tarallo M G Iwata G Z Zelevinsky T 2016 Phys. Rev. 93 032509
[12]	Xu L Yin Y Wei B Xia Y Yin J P 2016 Phys. Rev. 93 39
[13]	Gao Y F Gao T 2014 Phys. Rev. 90 052506
[14]	Zhang Y G Zhang H Dou G 2017 Acta Phys. Sin. 66 233101 in Chinese
[15]	Lane I C 2012 Phys. Chem. Chem. Phys. 14 15078
[16]	Cade P E Huo W M 1967 J. Chem. Phys. 47 649
[17]	Wan M J Shao J X Huang D H Jin C G Yu Y Wang F H 2015 Phys. Chem. Chem. Phys. 17 26731
[18]	Wells N Lane I C 2011 Phys. Chem. Chem. Phys. 13 19018
[19]	Nguyen J H V Odom B 2011 Phys. Rev. 83 053404
[20]	Gao Y Gao T 2015 Phys. Chem. Chem. Phys. 17 10830
[21]	McKellar A Richardson E H 1955 Astrophys. J. 122 196
[22]	Chen P Pallix J B Chupks W A Colson S D 1986 J. Chem. Phys. 84 527
[23]	Huber K P Herzberg G 1979 Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules New York Van Nostrand Reinhold Company Inc. 10.1007/978-1-4757-0961-2_2
[24]	Kalemos A Mavridis A Metropoulos A 1999 J. Chem. Phys. 111 9536
[25]	Kleinschmidit M Fleig T Marian C M 2002 J. Mol. Spectrosc. 211 179
[26]	Hettema H Yarkony D R 1994 J. Chem. Phys. 100 8991
[27]	Li Q Zhu Z H 2006 Acta Phys. Sin. 55 102 in Chinese
[28]	Sun H Freed K F 2003 J. Chem. Phys. 118 8281
[29]	Richards W G Cooper D L 1981 J. Phys. B: At. Mol. Phys. 14 L131
[30]	Zachwieja M 1995 J. Mol. Spectrosc. 170 285
[31]	Kasdan A Herbst E Lineberger W C 1975 Chem. Phys. Lett. 31 78
[32]	kepa R Para A Rytel M Zachwieja M 1996 J. Mol. Spectrosc. 178 189
[33]	Kumar A Hsiao C C Hung W C Lee Y P 1998 J. Chem. Phys. 109 3824
[34]	Herzberg G Johns J W C 1969 Astrophys. J. 158 399
[35]	Werner H J Knowles P J Lindh R Knizia G Manby F R Schütz M 2010 MOLPRO Version 2010.1, a package of ab initio programs see http://www.molpro.net
[36]	Knowles P J Werner H J 1985 J. Chem. Phys. 82 5053
[37]	Knowles P J Werner H J 1985 Chem. Phys. Lett. 115 259
[38]	Xia W Fu M Ma H Bian W 2017 Chem. Phys. 485 29
[39]	Werner H J Knowles P J 1988 J. Chem. Phys. 89 5803
[40]	Knowles P J Werner H J 1988 Chem. Phys. Lett. 145 514
[41]	You Y Yang C L Wang M S Ma X G Liu W W 2015 Phys. Rev. 92 032502
[42]	Laughoff S R Davidson E R 1974 Int. J. Quantum Chem. 8 61
[43]	Douglas N Kroll N M 1974 Ann. Phys. 82 89
[44]	Hess B A 1986 Phys. Rev. 33 3742
[45]	Di Rosa M D 2004 Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 31 395
[46]	Le Roy R J 2015 LEVEL 8.2: A computer program for solving the radial Schrödinger equation for bound and quasibound levels, Chemical Physics Research Report CP-668 University of Waterloo 10.1016/j.jqsrt.2016.05.028
[47]	Herzberg G 1950 Molecular spectra and molecular structure: spectra of diatomic molecules 1 6 273
[48]	Zhang Y G Zhang H Song H Y Yu Y Wan M J 2017 Phys. Chem. Chem. Phys. 19 24647
[49]	Wan M J Yuan D Jin C G Wang F H Yang Y J Yu Y Shao J X 2016 J. Chem. Phys. 145 341
[50]	Fu M Cao J Ma H Bian W 2016 Rsc. Adv. 6 100568
[51]	Fu M Ma H Cao J Bian W 2016 J. Chem. Phys. 144 184302
[52]	Fu M Ma H Cao J Bian W 2017 J. Chem. Phys. 146 134309