† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11405158 and 11775203) and the Presidential Foundation of China Academy of Engineering Physics (Grant No. YZJJLX 2016007).
We develop a rapid and convenient experimental method of absolutely calibrating the transmission of an x-ray flat-response filter. The calibration experiment is performed on a small laser-target facility, and a set of high resolution holographic flat-field grating spectrometers is used as a discrimination system of the laser-produced x-ray source. Given that the holographic flat-field grating has a relatively large width, the grating is divided into two regions for use in that direction, where one region has the filter added and the other region does not. The filter transmission is determined by dividing the x-ray signal counts detected when the filter is in the line of sight by those detected when the filter is out of the line of sight. We find that the calibration results of this experiment agree with the calibration results using a synchrotron radiation source, as well as simulation results. Our method is not only highly reliable but also rapid and convenient.
Indirect drive inertial confined fusion (ID ICF) is one of the main fusion ICF schemes.[1–4] The x-ray filters have been extensively used in the research field of ID ICF for blocking target debris, eliminating stray light, or attenuating the x-ray signal intensity.[5–7] However, due to their positions that just face to the chamber center, x-ray filters are often destroyed by target debris or contaminated by oil molecules. Thus, x-ray filters need to be calibrated regularly to obtain a real transmission value. The synchrotron radiation source is very suitable for calibrating filter transmission because of its characteristic wide spectral range, good brightness, and monochromaticity, and the corresponding calibration accuracy is quite high.[5,8] However, there are also many disadvantages: the beam line availability and the logistics of setting up the experiment usually take several weeks to months,[8,9] and the fixed location and fixed size of different devices of the synchrotron radiation facility and the beam uniformity severely constrain the size and location of the x-ray filter, which can be calibrated.[10,11] In addition, a Henke source can also be considered as a source for calibrating filter transmission.[7,12,13] Unfortunately, the anode material, electrical system limitations, and secondary fluorescent materials limit the intensity of the source, which leads to a low calibration accuracy.[5,9] An electron beam ion trap facility can also be used as an excellent x-ray source for calibrating x-ray filters. Brown et al. performed an x-ray blocking filter calibration experiment on the electron beam ion trap facility at the Lawrence Livermore National Laboratory.[9] The calibration accuracy of the experiments is good, however, there are relatively few electron beam ion trap facilities in some countries.
In recent years, many researchers have been attracted by laser-produced x-ray sources due to their high intensity and easy availability.[11,14] Using a laser-produced x-ray source coupled with various types of dispersion systems, many devices such as streak cameras,[15] x-ray CCD cameras,[16] and grating spectrometers[17] have been absolutely calibrated. Mirror-filters[18] and transmission grating spectrometers[19] are the two most commonly selected dispersion systems for these calibration experiments. To the best of our knowledge, no results have yet been reported on the calibration of a filter’s transmission based on a laser-produced x-ray source. In this paper, we introduce in detail a filter transmission calibration experiment on a small laser-target facility. We choose the novel compound filter developed by our research team as the calibration object of this experiment.[10] Here, the novel compound filter consists of two Au foils, with thickness values of 0.05 μm and 0.4 μm, respectively. The 0.4-μm foil consists of an array of pinholes each with a diameter of 5 μm and a distance of 11 μm between the pinholes. In this paper, we refer to the novel compound filter as a flat-response filter. Given that traditional dispersion systems (mirror-filters and transmission grating spectrometers) have a low spectral resolution and cumbersome spectra unfolding process, we choose a set of high resolution holographic flat-field grating spectrometers as the discrimination system of the laser-produced x-ray source. The holographic flat-field grating can suppress higher order diffraction effectively so that the detected signal in our calibration experiment does not need a cumbersome spectra unfolding process. In view of the fact that the holographic flat-field grating has a large width, the grating is divided into two regions. In one region we add the flat-response filter, and in the other region nothing is added. The filter transmission can be determined by dividing the x-ray signal counts detected in the region where the filter is in the line of sight by those detected in the region where the filter is out of the line of sight. The rest of this article is organized as follows. We first introduce in detail the experimental setup in Section
The calibration experiments were performed on a 100-J laser facility at the Research Center of Laser Fusion of the Chinese Academy of Engineering Physics, and the schematic diagram of the experiment setup is shown in Fig.
Figure
 | Fig. 3. (color online) Images obtained from two different regions on the flat focal plane: (a) region I and (b) region II. |
Given that the x-ray transmission of the flat-response filter is wavelength dependent, we first need to identify the wavelengths of these spectral lines. Here, the wavelengths of several strong lines can be identified by using the National Institute of Standards and Technology’s (NIST) Atomic Spectra Database[20] or the results of the part identified in Ref. [20]. According to the above two methods, however, it is difficult to identify the wavelengths of all spectral lines. According to several spectral lines, we precisely calibrate the relationship between the x-ray wavelength and the pixel position on the x-ray CCD by using the proposed parameter fitting method in Ref. [20]. In Fig.
 | Fig. 4. (color online) Layout diagram of holographic flat-field grating under real experimental conditions. |
According to the geometry relationship in Fig.
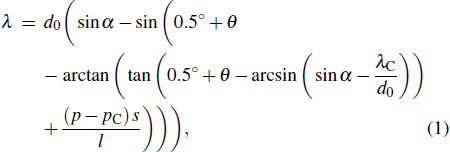
As shown in Fig.

Figure
Comparing these three results, we find that the calibration results of this experiment are in good agreement with the results obtained using the Beijing synchrotron radiation source and with the simulation results in the whole spectral region. Some data points in the results of this experiment deviate slightly from the results obtained using the synchrotron radiation source and also from the simulation results. It is not clear yet what causes this deviation. It may be attributed to the consistency of the width at different locations on the entrance slit. In addition, the selection of the subtracted background noise and bremsstrahlung radiation counts in data processing might be the reason. However, the deviation is small with respect to the experimental results obtained using the synchrotron source and the simulation results. Hence, our calibration method can also achieve high accuracy.
We have performed a transmission calibration experiment for a flat-response filter on a small laser-target facility. A set of holographic flat-field grating spectrometers is used as a dispersion system for the laser-produced x-ray source. Taking advantage of the width, the flat-field grating is divided into two regions. The calibration experiment uses only one laser-target test, so the calibration efficiency is very high. The whole process of the experiment may only take an hour or less. Of course, the selection of the target is very important because the calibration experiment requires multiple line spectra to calibrate the transmission of multiple energy points. In addition, our experiment only needs one set of holographic flat-field grating spectrometers as the measurement system, so the experimental processing is also very convenient. Moreover, our measurement method can be generalized to other energy regions by using different holographic flat-field gratings. By comparing the corresponding results, we see that the calibration results of this experiment are in good agreement with the calibration results obtained using the synchrotron radiation source, as well as with the simulation results. Hence, this method can be considered as an alternative for high accuracy transmission calibration of flat-response filters. Unlike calibration experiments using a synchrotron source facility or an electron beam ion trap facility, our method removes experimental facility restrictions on the time and place of calibration because small laser facilities are more common.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] |





