† Corresponding author. E-mail:
Project partially supported by the National Key Research and Development Program of China (Grant No. 2016YFB1000902), the National Natural Science Foundation of China (Grant Nos. 61232015 and 61621003), the Knowledge Innovation Program of the Chinese Academy of Sciences (CAS), and Institute of Computing Technology of CAS.
The stabilizer group for an n-qubit state |ϕ⟩ is the set of all invertible local operators (ILO) g = g1 ⊗ g2 ⊗ ⋯ ⊗ gn, 
Quantum entanglement[1] is a valuable resource for a variety of tasks that cannot be finished by classical resource. Among the most popular tasks are quantum teleportation[2] and quantum superdense coding.[3] Due to the importance of quantum entanglement, the classification of quantum entanglement states is a big issue for the quantum information theory.
Entanglement theory is a resource theory with its free transformation is local operations and classical communication (LOCC). As LOCC is hard to deal with mathematically, and with the number of the parties of the quantum systems growing, the classification of all entanglement states under the LOCC restriction becomes very hard. A conventional way is to consider other operations, such as stochastic LOCC (SLOCC), local unitary operations (LU), and separable operations (SEP).
Two n-partite states |ϕ⟩ and |ψ⟩ are SLOCC equivalent[4] if and only if there exists n invertible local operations (ILO) Ai, i = 1, 2,..., n such that

SEP is simple to describe mathematically and contains LOCC strictly, as pure state transformations exist belonging to SEP, but they cannot be achieved by LOCC. The authors in Ref. [11] presented that the existence of transformations under separable operations between two pure states depends largely on the stabilizer of the state. Recently, Gour et al. showed that almost all of the stabilizer group for 5 or more qubits pure states contains only the identity.[12] The authors in Ref. [13] generalized this result to n-qudit systems when n > 3, d > 2.
Symmetric states belong to the space that is spanned by the pure states invariant under particle exchange, and there are some results done on the classifications under SLOCC limited to symmetric states.[14–18] The authors in Ref. [15] proved if |ψ⟩ and |ϕ⟩ are n-qubit symmetric pure states, and n invertible operations Ai, i = 1, 2,..., n exist such that |ψ = A1 ⊗ A2 ⊗ ⋯ ⊗ An |ϕ⟩, then there exists an invertible matrix A such that

In this article, we consider the problem on the stabilizer groups for n-qubit symmetric states. This article is organized as follows. In Section
In this section, we will first recall the definition of symmetric states, and then we present the Majorana representation for an n-qubit symmetric pure state.
A pure state 
We call an n-partite pure state |ψ⟩ symmetric state if it is invariant under permuting the particles. That is, for any permutation operator Pπ, Pπ |ψ⟩ = |ψ⟩. Generally, there are two main characterizations for an n-qubit symmetric pure state |ψ⟩, Majorana representation[19] and Dicke representation. The Majorana representation for an n-qubit symmetric pure state is that single particles |ϕi⟩, i = 1, 2,..., n, exist such that




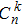
Next we introduce an isometric linear map


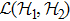
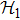

(i) Assume 

(ii) Assume 

Then we recall the definition and some important properties of the Möbius transformation, which is useful for the last part of this article. The Möbius transformation is defined on the extended complex plane onto itself,[20] it can be represented as

Möbius transformation maps circles to circles.
Möbius transformations are conformal.
If two points are symmetric with respect to a circle, then their images under a Möbius transformation are symmetric with respect to the image circle. This is called the “Symmetry Principle”.
With the exception of the identity mapping, a Möbius transformation has at most two fixed points.
There exists a unique Möbius transformation sending any three points to any other three points.
The unique Möbius transformation z → M(z) sending three points q, r, s to any other three points q′, r′, s′ is given by

The Möbius transformation forms a group, Möbius transformation is isotropic to the projective linear group PSL(2, ℂ) ≅ SL(2, ℂ)/{I, −I}.
As we know, the stereographic projection is a mapping that projects a sphere onto a plane. This projection is defined on the whole sphere except a point, and this map is smooth and bijective. It is conformal, i.e., it preserves the angles at where curves meet. By transforming the majorana points of a pure state |ψ⟩ to an extended complex plane, we may get the following proposition.[21]
At last, we recall two parameters defined in Ref. [14], the diversity degree and degeneracy configuration of an n-qubit symmetric pure state. Both parameters can be used to identify the SLOCC entanglement classes of all n-qubit symmetric pure states. Assume |ψ⟩ is an n-qubit symmetric pure state,

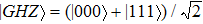
First we present that the stabilizer group for a two-qubit symmetric pure state 
Now we present a lemma to show an n-qubit symmetric pure state owns a nontrivial stabilizer group when n = 3, 4.
In Ref. [14], the authors presented that a three-qubit symmetric pure state is SLOCC equivalent to |W⟩ or |GHZ⟩. As we know, when we choose

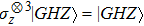



Here we denote




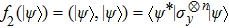



Apply ⟨0| ⊗ I⊗(n−1) to the left-hand side (LHS) and the right-hand side (RHS) of the above equality, and we denote that |ζ1⟩ = xk|D(n − 1, k)⟩ + xl|D(n − 1, l)⟩, |ζ2⟩ = xk|D(n − 1, k − 1)⟩ + xl|D(n − 1, l − 1)⟩ + xn|D(n − 1,n − 1)⟩, then

Assume n is odd, then by using f2(·) to the equality (


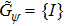
When n is even, we use f4(·) to the equality (

Then we present a class of symmetric critical states |ψ⟩ with Gψ = {I}. First we present the definition of critical states and a meaningful characterization of critical states. The set of critical states is defined as:

Here we present another proof on GLn = {I}, |Ln⟩ is defined in the equality (
Finally, I would like to apply Möbius transformation to show when the diversity number m of an n-qubit symmetric pure state |ψ⟩ is 5 or 6, the stabilizer group of |ψ⟩ is trivial, when m ≥ 7, under a conjecture we make, the stabilizer group of |ψ⟩ is trivial.
Assume a pure symmetric state |ψ⟩ can be represented in terms of Majorana representation:




Assume the diversity number of a symmetric state |ψ⟩ is m, the divergence configuration for the state |ψ⟩ is {k1, k2,..., km} with k1 ≥ k2 · ≥ km and Σiki = n. Then from the Lemma
Here we only consider the first two cases, the other two are similar to the second one. In case I), from property vi) of Möbius transformation f, we have








Here we note that when |ψ⟩ is a four-qubit symmetric pure state, |ψ⟩ always owns a nontrivial stabilizer group. As the diversity configuration can only be {1, 1, 1, 1}, {2, 1, 1}, {3, 1}, or {4}, from the above analyses, we see that the stabilizer group is nontrivial.
When m = 5, assume the degeneracy configuration of the pure state |ψ⟩ is {k1, k2, k3, k4, k5}. First we analyze the case when k1 = k2 = k3 = k4 = k5, if the stabilizer group is nontrivial, then there exists a nontrivial Möbius transformation f that can permute zi, i = 1, 2, 3, 4, 5, and we need to consider the following cases,
Similar to the analysis when m = 4, we have that the above case c) is invalid. For case d), we can consider the Möbius transformation g = f ○ f, as g(z1) = z3, g(z2) = z1, g(z3) = z2, g(z4) = z4, g(z5) = z5, so Case d) is invalid. For Case e), we can get












When m = 6, assume the degeneracy configuration of |ψ⟩ is {k1, k2,..., k6} with k1 = k2 = ⋯ = k6, here we first present that there cannot exist a Möbius transformation f such that f(z1) = z2, f(z2) = z3,..., f(z5) = z6, f(z6) = z1. Here we also apply the method reductio ad absurdum. If there exists a Möbius transformation f satisfying f(z1) = z2, f(z2) = z3,..., f(z5) = z6, f(z6) = z1, due to the property vi) of Möbius transformation, we have








Combining the results when m = 5, 6, we may conjecture that:
In this article, we consider the stabilizer group for a symmetric state |ψ⟩. First we present that the stabilizer group for an n-qubit symmetric state |ψ⟩ contains more than the identity when n = 2, 3, 4; then similar to the method presented in Ref. [12], we give a class of states whose stabilizer group contains only the identity; we also propose a class of states |ψ⟩ with 

| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] |


