While quantum cryptography has achieved great success in many cryptographic tasks such as quantum key distribution,^[1] there are also some tasks which are known to be hard. Oblivious transfer (OT),^[2,3] being an essential primitive for building two-party and multi-party secure computation protocols,^[4] is unfortunately covered. Because of the existence of the so-called honest-but-curious attack,^[5–9] and also partly due to the lack of a self-consistent definition of OT specifically made for the quantum case (as elaborated near the end of Section 5 of Ref. [10]), unconditionally secure quantum OT was proven to be impossible.^[11,12] Therefore, researchers sought for practically secure OT in recent years.^[13–29]

Recently, Nagy et al.^[30] proposed a very feasible quantum OT protocol, which does not require quantum storage when all participants are honest. The authors proved that the protocol is secure against individual measurements, as well as 2-qubit entanglement-based attacks. Later, however, we found that it is insecure against 5-body entanglement-based attacks.^[31] More rigorously, the goal of OT is to provide a method for the sender Alice to transfer a secret bit b to the receiver Bob, and it is called secure if Bob can obtain b unambiguously with probability 1/2 only, while Alice does not know whether Bob has learned b or not. We showed in Ref. [31] that if Bob has the technology to handle 5-body entangled states, then in the protocol of Ref. [30], he can learn b unambiguously with probability 62.5% using von Neumann measurements, or 64.6% using positive operator-valued measure (POVM).

These findings lead us to the question what is the exact security bound of the protocol between 2-qubit entanglement-based attacks and 5-body entanglement-based attacks. In the current paper, we will close the gap by showing that 4-body entangled states can still enable Bob to cheat, while 3-body entangled states are insufficient for him to learn b unambiguously with a probability higher than 1/2.

The paper is organized as follows. We will first review the OT protocol of Ref. [30] in Section 2. Then in Section 3, we will use the N = 1 case of the protocol as an example, to elaborate the cheating strategy using 4-body entangled states. The cheating strategy on protocols with arbitrary N will be provided in Section 4. Finally, the cheating using 3-body entangled states will be analyzed in Section 5.

Let {|0⟩, |1⟩} be the computational basis of a qubit. Denote the Hadamard basis as {|+⟩, |−⟩}, where |±⟩ ≡ (|0⟩ ± |1⟩)/. The OT protocol of Ref. [30] contains the following steps.

(i) Bob sends Alice M qubit sequences. Each sequence contains 4N qubits, where each of the states |0⟩, |1⟩, |+⟩, and |−⟩ appears N times, while the order is random. After receiving the qubits, Alice measures them all in one of the two bases (computational or Hadamard) and records the outcomes.

(ii) Alice verifies with Bob that the sequences received correspond to the agreed specifications. The details of this verification were provided in Section 3 of Ref. [30]. In brief, she picks a sequence and asks Bob to announce the state of each qubit, and checks whether the announced numbers of |0⟩, |1⟩, |+⟩, and |−⟩ in this sequence are equal. She also checks whether Bob has announced the states honestly using her own measurement outcomes on these qubits. All but one of the M sequences are checked and then discarded in this step. The sequence that is not verified is selected randomly among the M sequences received, and if the verification is successful, she assumes that the remaining unchecked sequence also contains equal numbers of |0⟩, |1⟩, |+⟩, and |−⟩.

(iii) Alice randomly chooses one qubit from the remaining sequence, and looks at the value measured in step (i). If the outcome of this measurement was |0⟩ or |+⟩, she sends the bit b she wants to transmit over to Bob through a classical channel. Or if the outcome of this measurement was |1⟩ or |−⟩, she sends (i.e., the complement of her bit b) to Bob.

(iv) Now Alice tells Bob which qubit she chose in step (iii) and which basis she used for measuring this qubit. If her measurement basis is identical to the one in which Bob prepared that qubit in step (i), then Bob knows the value of b (note that if the outcome of Alice’s measurement is |1⟩ or |−⟩, Bob has to complement the bit value received). Otherwise, Bob obtains no information on b.

Now we will show that if Bob is dishonest and he has the technology to handle 4-body entangled states, then he can learn Alice’s secret bit b unambiguously with a probability higher than 1/2, making the protocol insecure.

For easy understanding, we first describe the cheating strategy in the protocol where M (the total number of qubit sequences) can be arbitrary, while each sequence merely contains four qubits, i.e., N = 1. According to the protocol, when Bob is honest, he should prepare the states of the four qubits as |0⟩, |1⟩, |+⟩, and |−⟩, respectively, with a random order. However, a dishonest Bob can cheat as follows.

In step (i) of the protocol, for the four qubits A₁, A₂, A₃, and A₄ in each of the M sequences, dishonest Bob introduces an additional 6-level quantum system B, and prepares their initial state as

Bob then sends qubits A₁, A₂, A₃, and A₄ to Alice, while keeping system B privately at his side. In step (ii) of the protocol, once such a sequence is selected for verification, Bob uses {|l₁, . . ., |l₆⟩} as the basis and measures B. If the measurement outcome is |l_i0⟩, he announces the state of the qubits A₁, A₂, A₃, and A₄ as |0⟩ ⊗ P_i0(|1⟩ |+⟩ |−⟩). It is trivial to show that he can always pass the verification in step (ii) successfully with this method. On the other hand, consider the case when such a sequence is not chosen for verification. Instead, it is picked for transferring Alice’s secret bit b in steps (iii) and (iv). Since Alice randomly selects one of the qubits in this sequence to encode b, there can be four cases.

(I) Alice picks qubit A₁, which occurs with probability p₁ = 1/4.

Bob cannot cheat in this case since A₁ was actually prepared honestly following the protocol. Thus he can learn the value of Alice’s b with probability r₁ = 50% only, as it is expected in the original protocol.

(II) Alice picks qubit A₂, which occurs with probability p₂ = 1/4. This case can be further broken down to two possibilities.

(II-1) Alice measures A₂ in the basis {|+⟩, |−⟩}, which occurs with probability p_2.1 = 1/2 when case (II) indeed happens.

Bob keeps system B unmeasured until the end of step (IV). Then after Alice reveals to Bob that she has used {|+⟩, |−⟩} as the basis for measuring system A₁, Bob measures system B in the basis {|l₁⟩, . . ., |l₆⟩}. If the result belongs to the subset {|l₃⟩, |l₄⟩, |l₅⟩, |l₆⟩} (which occurs with probability p_2.1.1 = 2/3, as can be seen from Eq. (1)), he can deduce whether qubit A₂ has collapsed to the state |+⟩ or |−⟩, and learns Alice’s secret bit b with probability r_2.1.1 = 100%.

On the contrary, there is the probability p_2.1.2 = 1/3 that Bob’s measurement result of B belongs to the subset {|l₁⟩, |l₂⟩}. It indicates that the state of A₂ has collapsed to |1⟩_A2. In this case, Bob cannot learn Alice’s b at all, because either one of the two results |+⟩ and |−⟩ is possible when Alice measures |1⟩_A2 in the basis {|+⟩, |−⟩}.

(II-2) Alice measures A₂ in the basis {|0⟩, |1⟩}, which occurs with probability p_2.2 = 1/2 when case (II) indeed happens.

In this case Bob tries to project system B into the subspace supported by {|l₁⟩, |l₂⟩} using the projective operator

On the contrary, there is the probability p_2.2.2 = 2/3 that the above projection will fail. Then the state of A₂ ⊗ A₃ ⊗ A₄ ⊗ B will collapse from Eq. (1) into

This equation implies that if Bob can discriminate the state from the state , then he is able to deduce whether Alice’s qubit A₂ has collapsed to |0⟩ or |1⟩, and therefore learn Alice’s bit b. To study the probability for this state discrimination, let us find out the reduced density matrices ρ_j of Bob’s system B corresponding to (j = 0,1), which are defined as

The von Neumann projection operators for discriminating ρ₀ and ρ₁ can be constructed as

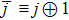
As a result, if Bob can apply von Neumann measurements only, once the operator M_B in Eq. (2) fails to project system B into the subspace supported by {|l₁⟩, |l₂⟩}, all Bob needs to do is to measure system B with either the operator M₀ or M₁ randomly. If what he applied is M_j (j ∈ {0,1}) and Alice’s qubit A₂ is in the state |j⟩, the probability for his projection to be successful is Tr(M_jρ_j). On the other hand, from Eq. (11) we know that if the state of Alice’s qubit A₂ is , then his projection can never be successful. As Bob picks M₀ or M₁ with the same probability, there is probability 1/2 that he happens to pick M_j while qubit A₂ is in the state |j⟩, so that he can discriminate the state of qubit A₂ unambiguously and deduce the value of Alice’s b with probability Tr(M_jρ_j). Namely, the probability for him to learn b unambiguously is

Moreover, if Bob owns the technology to perform a positive operator-valued measure (POVM), he can further increase this probability. As elaborated in Ref. [32], the POVM for optimum unambiguous discrimination of the density matrices ρ₀ and ρ₁ is {Π₀, Π₁, Π₂}, with

As a brief summary of the above results, in case (II-2) Bob applies the operator M_B in Eq. (2) on system B first. With probability p_2.2.1 = 1/3 the projection can be successful and he learns the value of b with probability r_2.2.1 = 100%. With the rest probability p_2.2.2 = 2/3 the projection fails. In this case Bob continues by applying the von Neumann measurement in Eq. (10) or the POVM in Eq. (14), depending on what technology is available to him. Then he can learn the value of b with probability r_von = 12.5% or r_POVM = 14.6%, respectively. Therefore, the average probability for him to learn b unambiguously in case (II-2) is r_2.2 = p_2.2.1r_2.2.1 + p_2.2.2r_von = (1/3) × 100% + (2/3) × 12.5% = 41.6% for von Neumann measurement or r_2.2 = p_2.2.1r_2.2.1+p_2.2.2r_POVM=(1/3) × 100% + (2/3) × 14.6% = 43.1% for POVM.

Consequently, the total probability for Bob to learn b unambiguously in case (II) is

(III) Alice picks qubit A₃, which occurs with probability p₃ = 1/4.

From the symmetric form of qubits A₂, A₃, and A₄ in Eq. (1), we can see that the above analysis on case (II) also applies here. Thus, in the current case Bob can learn b unambiguously with probability r₃ = r₂.

(IV) Alice picks qubit A₄, which occurs with probability p₄ = 1/4.

For the same reason in case (III), the probability for Bob to learn b unambiguously in this case also satisfies r₄ = r₂.

As a result, the overall probability for Bob to learn b unambiguously in all the four cases is

Also, instead of Eq. (1), it is not hard to see that Bob can cheat by preparing the initial state as either

Now we proceed to show that even if we increase the value of the security parameter N in the protocol of Ref. [30], the probability of catching Bob’s attack cannot be raised.

The cheating strategy is not much different from the one in the N = 1 case. For any N > 1, in step 1 of the protocol dishonest Bob simply prepares MN copies of 4-body entangled states. Each copy still takes the form of Eq. (1). Again, he sends the first four qubits of each copy to Alice, so that these qubits in all copies form the M sequences required in the protocol. The order of the qubits in each sequence can even be randomized too, as long as Bob himself remembered which qubits are the ones that belong to the same copy of the 4-body entangled states.

The remaining steps of the attack are exactly the same as that of the N = 1 case. Namely, in step (II) of the protocol, once a sequence of qubits is selected for verification, Bob measures system B in each copy of the 4-body entangled states in the basis {|l₁⟩, . . ., |l₆⟩}. As mentioned above, with this method he can always know what can be disclosed as the states of the qubits A₂, A₃, and A₄ without causing any conflict with Alice’s own measurement results.

Later in steps (III) and (IV) of the protocol, Bob waits until Alice discloses the position and her measurement basis on the qubit that she eventually selected for encoding the secret bit b. Then he finds out the copy of the 4-body entangled states which contained this qubit, and measures the corresponding system B with the operators that we presented in Eq. (10) or Eq. (14).

It is not hard to see that finally, Bob is still able to obtain the value of Alice’s secret bit b unambiguously with probability 53.1% when using von Neumann measurement, or 53.7% when using POVM, as he did in the protocol with N = 1. That is, by increasing the value of N, dishonest Bob merely needs to raise the total number of the copies of the 4-body entangled states. He can achieve the same probability for successful cheating, without the need to entangle the quantum systems from different copies together. In short, increasing N will not make it harder for Bob to cheat. Also, as our above analysis on the N = 1 case does not put any restriction on the value of M, we arrive at the conclusion that both the security parameters N and M have little to do with the difficulty of the practical implementation of Bob’s cheating, and they are completely unhelpful for reducing Bob’s probability of successfully cheating. Simply put, even if we merely choose N = M = 1, the security level of the resultant protocol is exactly the same as the protocols with higher N, M values.

Here we will show that Bob cannot cheat if he can handle 3-body entanglement only. Again, taking the N = 1 case as an example, as he needs to keep one of the quantum system at his side, a 3-body entangled state used for his cheating can contain two of Alice’s qubits at the most. In each of the M sequences sent to Alice which contain four qubits A₁, A₂, A₃, and A₄, once the sequence is chosen in step 2 for verification, Bob needs to show that all the four states |0⟩, |1⟩, |+⟩, and |−⟩ are presented. Without loss of generality, suppose that qubits A₁ and A₂ already took over the states |1⟩ and |−⟩ (or |+⟩ and |−⟩), respectively (regardless whether Bob prepared A₁ and A₂ in these states using entanglement or not). Then the states of A₃, A₄ can only be chosen among {|0⟩, |+⟩} (or {|0⟩,|+⟩}). Thus, in place of the 4-body entangled state Eq. (1), Bob has to prepare the initial state of the 3-body entangled system as either

i) Suppose that Bob prepares the initial state as .

If Alice announces in step 4 that her measurement basis on A₃ is {|0⟩, |+⟩}, Bob can expand as

Similarly, from the symmetry of |0⟩_A3 and |+⟩_A3 in Eq. (21), it can be shown that if Alice’s measurement basis on A₃ is {|+⟩, |−⟩}, Bob also stands a probability 1/2 to learn b unambiguously. That is, preparing the initial state in the 3-body entangled form of equation (21) does not bring an extra advantage for Bob than following the original protocol honestly.

ii) Suppose that Bob prepares the initial state as .

If Alice announces in step 4 that her measurement basis on A₃ is {|0⟩, |+⟩}, Bob can simply measure system B in the basis {|l₁⟩, |l₂⟩}. From Eq. (22) we immediately know that Bob can learn Alice’s measurement result and deduce her secret bit b with probability 100%.

However, if Alice announced the measurement basis on A₃ is {|+⟩, |−⟩}, equation (22) can be written as

Since the probabilities for Alice to choose the basis {|0⟩, |1⟩}, or {|+⟩, |−⟩} are both 1/2, we can see that the average probability for Bob to learn b unambiguously using Eq. (22) is 100% × (1/2) + 0% × (1/2) = 1/2, which is the same as that in the honest case too.

Thus it is shown that both the 3-body entangled states equations (21) and (22) cannot increase dishonest Bob’s probability for learning Alice’s b unambiguously.

So we see that if Bob is limited to the technology to prepare 3-body (or less) entangled states, the probability for him to learn Alice’s b unambiguously will remain to be 1/2, which is the same as that in the honest case where he does not apply the entanglement-based attacks.

To increase this probability, dishonest Bob should at least use 4-body entangled states. Then he can learn b unambiguously with probability 53.1% (using von Neumann measurement) or 53.7% (using POVM). It is lower than the values 62.5% (von Neumann measurement) or 64.6% (POVM) achieved by the cheating strategy proposed in Ref. [31] based on 5-body entangled states, and is merely a little higher than the value 1/2 in the honest case. However, it remain non-trivial, and like the strategy in Ref. [31], raising the number of qubits used in the protocol of Ref. [30] (i.e., the values of N and M) cannot lower this probability nor make it harder to cheat.

From a practical point of view, to implement the attack, Bob needs the capacity to prepare 4-body entangled states, and delay the measurement while keeping the entanglement from decoherence. At the end of the process, however, he merely needs to perform measurements on his system B alone. No need for collective measurements on the multi-system. Nevertheless, B is a 6%-level system as shown in Eq. (1). If such a system is implemented with qubits, then it takes 3 qubits so that there cannot be less than 6 orthogonal states. The 4-body entangled state will actually take 6 qubits to implement, and the measurement on system B will become a collective one on 3 qubits. Thus the protocol of Ref. [30] remains secure until this technology becomes available in the future. More interestingly, as increasing N and M is useless, the honest participants can simply run the protocol with N = M = 1, i.e., only 4 qubits are needed for implementing the protocol, which saves a lot of quantum resources.