Cite this Article
Gu Yan, Zhang Haifeng, Song Zhigang, Liang Jiuqing, Wei Lianfu. Extended Bell inequality and maximum violation. Chinese Physics B, 2018, 27(10): 100303  
Permissions
Extended Bell inequality and maximum violation
Gu Yan1, Zhang Haifeng1, Song Zhigang1, Liang Jiuqing1, †, Wei Lianfu2, 3
Institute of Theoretical Physics and Department of Physics, State Key Laboratory of Quantum Optics and Quantum Optics Devices, Shanxi University, Taiyuan 030006, China
State Key Laboratory of Optoelectronic Materials and Technologies, School of Physics and Engineering, Sun Yat-Sen University, Guangzhou 510275, China
Quantum Optoelectronics Laboratory, School of Physics and Technology, Southwest Jiaotong University, Chengdu 610031, China

 

† Corresponding author. E-mail: jqliang@sxu.edu.cn

Project supported in part by the National Natural Science Foundation of China (Grant Nos. 11275118 and U1330201).

Abstract

The original formula of Bell inequality (BI) in terms of two-spin singlet has to be modified for the entangled-state with parallel spin polarization. Based on classical statistics of the particle-number correlation, we prove in this paper an extended BI, which is valid for two-spin entangled states with both parallel and antiparallel polarizations. The BI and its violation can be formulated in a unified formalism based on the spin coherent-state quantum probability statistics with the state-density operator, which is separated to the local and non-local parts. The local part gives rise to the BI, while the violation is a direct result of the non-local quantum interference between two components of entangled state. The Bell measuring outcome correlation denoted by PB is always less than or at most equal to one for the local realistic model () regardless of the specific superposition coefficients of entangled state. Including the non-local quantum interference the maximum violation of BI is found as , which, however depends on state parameters and three measuring directions as well. Our result is suitable for entangled photon pairs.

PACS: 03.65.Ud;03.67.Lx;03.67.Mn;42.50.Dv
Keyword:Bell inequality;quantum entanglement;non-locality;spin coherent state
1. Introduction

The non-locality is the most striking characteristic of quantum mechanics beyond our intuition of space and time in the classical field theory.[1–3] It has no classical counterpart and therefore has been receiving continuously theoretical attention ever since the birth of quantum mechanics. The two-particle entangled-state as a typical example of non-locality was originally considered by Einstein–Podolsky–Rosen to question the complicity of quantum mechanics. It has become the essential ingredients in quantum information and computation.[4–6] The quantum nonlocal correlation by local measurements on distant parts of a quantum system is a consequence of entanglement, which is incompatible with local hidden variable models.[7] This was discovered by Bell, who further established a theorem known as Bell inequality (BI)[7] to provide a possibility of quantitative test for non-local correlations, which lead necessarily to the violation of BI. The overwhelming experimental evidence[8–13] for the violation of BI in some entangled-states invalidates local realistic interpretations of quantum mechanics. Various extensions of the original BI have proposed from both theoretical and experimental viewpoints.[14–21] The nonlocality has been also justified undoubtedly in various aspects.[14,15] Soon after the pioneer work of Bell, Clauser–Horne–Shimony–Holt (CHSH) formulated a modified form of the inequality,[22] which is more suitable for the quantitative test and therefore attracts most attentions of experiments. An alternative inequality for the local realistic model was formulated by Wigner[23–25] known as Wigner inequality (WI), which needs measurements of particle number probabilities only along one direction of spin-polarization. It is assumed that the joint probability distributions for measuring outcomes satisfy the locality condition[26] in the underlying stochastic hidden variable space. The experimental evidence strongly supports the quantum non-locality, however the underlying physical-principle is obscure.[27] Various aspects relating to the initial debate remain to be fully understood.

In order to have a better understanding of the underlying physics we in previous publications[28,29] formulated the BI and its violation in a unified formalism by means of the spin coherent-state quantum probability statistics along with the assumption of measurement-outcome-independence. The density operator of a bipartite entangled-state can be separated into the local and non-local parts,[29] with which the measuring outcome correlation is then evaluated by the quantum probability statistics in the spin coherent-state base vectors. The local part of density operator gives rise to the BI, while its violation is a direct result of non-local correlations of entangled states.[29] We predicted a spin parity effect[28] in the violation of BI, which is violated by the entangled-states of half-integer but not the integer spins. It was moreover demonstrated that the violation is seen to be an effect of Berry phase induced by relative-reversal measurements of two spins.

The original formula of BI is actually valid for arbitrary two-spin entangled-state with antiparallel polarization[30] beyond the singlet state. However, it has to be modified by the change of a sign for the parallel spin polarization.[29] It is an interesting question whether or not a unified inequality exists for both antiparallel and parallel spin-polarizations. It is the main goal of the present paper to establish an extended BI valid for two kinds of entangled states. Following the recent work for the maximum violation[31] of WI, the maximum violation bound of the BI is also obtained to demonstrate a fact that the BI with three-direction measurements is equally convenient as CHSH inequality for the experimental test. A loophole-free experimental verification of the violation of CHSH inequality was reported recently by means of electronic spin associated with a single nitrogen-vacancy defect center in a diamond chip[32,33] and also for the two-photon entangled states with mutually perpendicular polarizations.[34] The formalism and results in the present paper are also suitable for the entangled photon pairs.

2. Spin coherent-state quantum probability statistics and BI

In our formalism the Bell-type inequalities and their violation are formulated in a unified manner by means of the spin coherent-state quantum probability statistics.[28,29] We begin with an arbitrary two-spin entangled state with antiparallel polarization

where |±⟩ are considered as the usual spin-1/2 eigenstates . The normalized coefficients can be parameterized as c1 = eiηsin ξ, c2 = e−iη cos ξ in terms of the arbitrary real parameters η, ξ. The density operator of an entangled state can be separated to the local (or classical) and non-local (or quantum coherent) parts such that

The local part

which is the classical two-particle probability-density operator, gives rise to the local realistic bound of measuring outcome correlation, namely the BIs. While the non-local part

describing the quantum coherence between two remote spins results in the violation of the BIs.[28,29] For the entangled state of parallel polarization

the local and non-local parts of density operator become[29]

and

respectively.

2.1. Spin measuring outcome correlation and BI

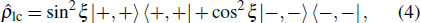
We assume to measure two spins independently along two arbitrary directions, say a and b. Each measuring outcome falls necessarily into the eigenvalues of projection spin-operators and , i.e.,

according to the quantum measurement theory. Solving the above eigenvalue equations for each direction r (r = a, b) we obtain two orthogonal eigenstates given by

where the unit vector r = (sin θr cos ϕr, sin θr sin ϕr, cos θr) is parameterized with the polar and azimuthal angles θr, ϕr. The two orthogonal states |±r⟩ are known as spin coherent states of north- and south-pole gauges.[35–37] The eigenstates of projection spin-operators and form a measuring-outcome independent vector base for two spins measured respectively along the a, b directions. The four base vectors are labeled as

for the sake of simplicity. The measuring outcome correlation[29,30] is obviously

where

is the spin correlation operator and (i = 1,2,3,4) denote matrix elements of the density operator. The measuring outcome correlation can be also separated to local and non-local parts

with

and

Submitting the local parts of density operators Eqs. (3) and (4) into the local measuring-outcome correlation Plc(a,b) we have

respectively for the antiparallel and parallel spin polarizations. The BI becomes correspondingly[28,29]

for the antiparallel and parallel entangled states.

2.2. Particle-number correlation probability

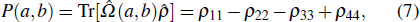
In the Wigner formalism[31] the particle-number correlation probability is considered instead of the spin measuring-outcome correlation. The quantity defined by

describes the particle-number correlation probability for two positive-spin particles measured respectively along a, b directions. Correspondingly we have

which are all positive quantities different from the spin measuring-outcome correlations. The spin measuring-outcome correlation P(a,b) in the BI are related to the four particle-number correlation probabilities by

which is the difference between the particle number probabilities of same direction measurement and that of opposite directions.

3. Extended BI and maximum violation

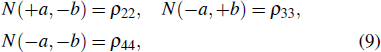
The extended BI for both parallel and antiparallel polarizations is obviously

for the local model, since

We define a quantum Bell correlation probability (QBCP) that

The extended BI is then

which is violated once PB > 1.

In Appendix A we specifically present a simple proof of the validity of the extended BI, in terms of the classical statistics with the particle-number correlation probabilities in the Wigner formulation.[23–25] An interesting question is to find the maximum violation bound, which is useful for the experimental verification.

3.1. Two-spin entangled state with antiparallel polarization

By means of the spin coherent-state quantum probability statistics we can obtain quantum correlation probability P(a,b) for the two-spin entangled state with antiparallel polarization. The entire (quantum) correlation-probability including the non-local parts becomes

The QBCP for the three-direction measurement is found as

Since the polar angle θ is restricted between 0 and π, the quantity sin θa sin θb is larger than or equal to zero. We then obtain after a simple algebra the inequality of QBCP

Thus we have the maximum violation bound

As a matter of fact the QBCP is bounded by 2 ≥ PB ≥ − 1.

For the measuring directions with polar and azimuthal angles θa = θb = θc = π/2 and ϕa = π/2, ϕb = 0, ϕc = π, the QBCP equation (11) becomes

The three directions of measurements a, b, and c are set up with a along positive y axis, b, c along positive and negative x axis respectively. The maximum violation is approached with the state parameters, for example, ξ = (π/4)mod2π,η = (π/4)mod 2π. The entangled state in this case is

The violation value depends not only on the entangled-state parameters ξ, η in our parametrization but also on the three directions of measurements.

Particularly for the two-spin singlet state

with the state parameters ξ = 3π/4, η = 0, the QBCP value is found from Eq. (11) as

for the polar angles of three-direction measurements θa = θb = θc = π/2. The maximum QBCP value of two-spin singlet is obtained as

for azimuthal angles ϕa = 3π/4, ϕb = π/2, ϕc = 0. It is less than the maximum violation bound different from the common believe that the spin-singlet gives rise to the maximum violation bound. To obtain the violation value for the spin singlet state the vector b is perpendicular to c and the vector a is parallel to the vector difference (b − c).

3.2. Parallel polarization

For the two-spin entangled state with parallel polarization[29]

the entire correlation–probability including the non-local parts becomes

The QBCP then is

from which we have the same inequality of QBCP as Eq. (12). Thus, the maximum value of QBCP is still

The maximum violation of BI can be realized from Eq. (13) for the parallel polarization state given by

with the state parameters ξ = (π/4)mod 2π,η = (π/4)mod 2π. The three-direction measurements should be arranged respectively with the polar and azimuthal angles θa = θb = θc = π/2, ϕa = π/2, φb = 0, φc = π. Namely a, b, c are perpendicular to the original spin polarization (z axis) with a along y direction; b, c along ±x directions.

In conclusion the value of QBCP is restricted by −1 ≤ PB ≤ 2 for two-spin entangled states with both parallel and antiparallel polarizations. The extended BI is violated if 1 < PB.

4. Polarization-entangled photon pairs

Polarization-entangled photon pairs play an important role in various quantum information experiments instead of the two-spin entangled state. We reformulate the extended BI and maximum violation in terms of our formalism.

4.1. Entangled photon pairs with mutually perpendicular polarizations

Two perpendicular polarization states of a single photon may be denoted by |ex⟩ and |ey⟩ in our framework, where we have assumed that the polarization plane is perpendicular to the z axis. The entangled state of a photon pair with mutually perpendicular polarizations can be represented as

which corresponds to the two-spin entangled state with antiparallel spin-polarizations. The normalized coefficients c1 and c2 are parameterized as in the spin case. The local and non-local parts of density operator are the same, however, with the spin states |±⟩ replaced respectively by the photon polarization states |ex⟩, |ey⟩. The entangled photon pairs are measured in three arbitrary directions, say a,b, and c, in the plane also perpendicular to the z axis. With respect to a measuring direction, say r = (cos ϕr, sin ϕr, 0) (r = a, b, c), the horizontal (h) and vertical (v) polarization states are represented as

where ϕr is the azimuthal angle of the measuring direction r. In the measuring-outcome independent vector base denoted similarly by

the local part of the density-operator elements becomes

The non-local part is

The local measuring-outcome correlation is

with which it is easy to verify the extended BI

Including the nonlocal part

the entire correlation-probability becomes

The QBCP is

which is then bounded by

From the general form of QBCP Eq. (16) it is easy to check that the entangled state

results in the maximum violation bound for the three-direction measurements with ϕa = π/8, ϕb = 3π/8, and ϕc = 15π/8. Namely, b is perpendicular to c, and the angle between a and c equals π/4. It is remarkably to find that the state

which may be regarded as the the counterpart of two-spin singlet, gives rise to the QBCP-value again less than the maximum bound . The three angles of measuring directions should be arranged as ϕa = 3π/8, φb = π/4, and φc = 0 in this state.

4.2. Parallel polarization

The state of entangled photon pairs with mutually parallel polarizations is

With the same calculation procedure we obtain the measuring outcome correlation

which has a sign difference with the perpendicular case of Eq. (14). The QBCP is invariant as Eq. (15) comparing with the entangled state with perpendicular polarizations, so is the extended BI. Including the nonlocal part Pnlc(a,b) = sin 2ξ sin 2ϕa sin 2ϕb cos 2η the entire correlation-probability is

The QBCP then is

which leads again to the maximum violation bound .

In the entangled state of equal polarizations

the maximum violation can be achieved from Eq. (19) for the same measuring directions of a, b, and c as in the state of Eq. (17).

5. Conclusions and discussions

The BI and its violation are formulated in a unified way by the spin coherent-state quantum probability statistics, in which the state density operator is separated to the local and nonlocal parts. The BI is a direct result of local model, while the nonlocal part from the coherent interference of two components of the entangled state leads to the violation. The original BI, which was derived from the two-spin singlet, is extended to a unified form valid for the general entangled state with both antiparallel and parallel polarizations. Up to date the experimental test[32–34] of the inequality violation are mainly focused on the CHSH form, which provides a qualitative bound of the violation. The maximum violation value of the extended BI is two times of BI bound unit one (), while it is times in the CHSH inequality case. We thus conclude that the extended BI is at least equally convenient for the experimental verification of its violation, which is expected in the future experiments. We moreover demonstrate that the violation value depends not only on the measuring directions but also two superposition coefficients of the entangled states, namely the angle parameters ξ, η in our formalism. It is remarkably to find that the maximum violation for the spin singlet is only less than the maximum violation bound . Our observation is different from the common believe that the spin-singlet would give rise to the maximum violation. The extended BI and violation are also suitable to entangled photon pairs. The BI and WI were formulated respectively with the spin and particle-number-probability correlations in the literature. The two measuring outcome correlations are also unified in our formalism of quantum probability statistics.[28,29,31]

Reference
[1] Su H Y Wu Y C Chen J L 2013 Phys. Rev. 88 022124
[2] Kwiat P G Barraza-Lopez S Stefanov A et al. 2001 Nature 409 1014
[3] Popescu S 2010 Nat. Phys. 6 151
[4] Nielsen M A Chuang I L 2011 Quantum Computation and Quantum Information Cambridge Cambridge University Press 1 59
[5] Bennett C H Divincenzo D P 2000 Nature 404 247
[6] Loss D DiVincenzo D P 1998 Phys. Rev. 57 120
[7] Bell J S 1964 Physics 1 195
[8] Waldherr G Neumann P Huelga S F Jelezko F Wrachtrup J 2011 Phys. Rev. Lett. 107 090401
[9] Sakai H Saito T Ikeda T et al. 2006 Phys. Rev. Lett. 97 150405
[10] Pal K F Vertesi T 2017 Phys. Rev. 96 022123
[11] Rowe M A Kielpinski D Meyer V et al. 2001 Nature 409 791
[12] Dada A C Leach J Buller G S et al. 2012 Nat. Phys. 7 677
[13] Gisin N Peres A 1992 Phys. Lett. 162 15
[14] Brito S G A Amaral B Chaves R 2018 Phys. Rev. 97 022111
[15] Pozsgay V Hirsch F Branciard C et al. 2017 Phys. Rev. 96 062128
[16] Groblacher S Paterek T Kaltenbaek R et al. 2007 Nature 446 871
[17] Buhrman H Cleve R Massar S et al. 2010 Rev. Mod. Phys. 82 665
[18] Cabello A Sciarrino F 2012 Phys. Rev. 2 021010
[19] Wei L F Liu Y X Nori F 2005 Phys. Rev. 72 104516
[20] Garcia-Patron R Fiurasek J Cerf N J et al. 2004 Phys. Rev. Lett. 93 130409
[21] Hess K Raedt H D Michielsen K 2017 J. Mod. Phys. 8 57
[22] Clauser J F Horne M A Shimony A Holt R A 1969 Phys. Rev. Lett. 23 880
[23] Wigner E P 1970 Am. J. Phys. 38 1005
[24] Sakurai J J Tuan S F Commins E D 1995 Am. J. Phys. 63 93
[25] Home D Saha D Das S 2015 Phys. Rev. 91 012102
[26] Das D Datta S Goswami S Majumdar A S Home D 2017 Phys. Lett. 381 3396
[27] Pawlowski M Paterek T Kaszlikowski D Scarani V Winter A Zukowski M 2009 Nature 461 1101
[28] Song Z Liang J Q Wei L F 2014 Mod. Phys. Lett. 28 1450004
[29] Zhang H Wang J Song Z et al. 2017 Mod. Phys. Lett. 31 1750032
[30] Grimme S 2003 J. Chem. Phys. 118 9095
[31] Gu Y Zhang H Song Z Liang J Q Wei L F 2018 Int. J. Quantum Inform. 16 1850041
[32] Hensen B Bernien H Dréau A E et al. 2015 Nature 526 682
[33] Hensen B Kalb N Blok M S et al. 2016 Sci. Rep. 6 30289
[34] Yin J Cao Y Li Y H Liao S K Zhang L Ren J G Cai W Q Liu W Y 2017 Science 356 1140
[35] Liang J Q Wei L F 2011 New Advances in Quantum Physics Beijing Science Press 56
[36] Bai X M Gao C P Li J Q Liang J Q 2017 Opt. Express 25 17051
[37] Zhao X Q Liu N Liang J Q 2014 Phys. Rev. 90 023622