† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11264015 and 11404150).
We investigate the dynamical behaviors of quantum-memory-assisted entropic uncertainty and its lower bound in the amplitude-damping channel. The influences of different placement positions of the quantum register on the dynamics of quantum coherence, quantum entanglement, and quantum discord are analyzed in detail. The numerical simulation results show that the quantum register should be placed in the channel of the non-Markovian effect. This option is beneficial to reduce the entropic uncertainty and its lower bound. We also find that this choice does not change the evolution of the quantum coherence and quantum entanglement, but changes the dynamical process of the quantum discord of the system. These results show that quantum coherence, quantum entanglement, and quantum discord are different quantum resources with unique characteristics and properties, and quantum discord can play a key role in reducing the uncertainty of quantum systems.
In recent years, quantum entanglement, quantum discord, and quantum coherence have been widely used as useful physical resources in quantum information processing.[1,2] In fact, quantum coherence is a fundamental quantum resource, and both quantum entanglement and quantum discord of the quantum system are closely related to quantum coherence. The research on quantum entanglement has received a great deal of attention and been widely investigated. At present, the theory of entanglement has been improved, and the experimental verification is quite complete, which has been widely applied in practice.[3–5] Quantum discord has also been studied extensively, which is more widespread than quantum entanglement in quantum systems.[6,7] Despite the fundamental importance of quantum coherence, the rigorous definition and effective measurement of quantum coherence have only recently been studied systematically.[8,9] The coherence of quantum systems is the basis of non-classical correlation, thus there should be some relation between quantum coherence and quantum correlation. Reference [10] proved the relation between quantum coherence and quantum discord in quantum systems, and described the condition of quantum coherence transformed into quantum discord. The research result obtained by Streltsov et al. showed that the necessary condition for the entanglement between two systems was that one of the quantum systems must have coherence.[11]
To describe the uncertainty of the quantum system, Heisenberg first proposed the uncertainty principle.[12] Subsequently, Kennard and Robertson extended the principle to a standard deviation given by[13,14]

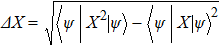
The Shannon entropy can be used to measure the uncertainty of a physical measurement. For this reason, Hirschman et al. used Shannon entropy to measure the uncertainty in quantum mechanics, and first proposed the entropic uncertainty relation between position and momentum.[15] Deutsch et al. extended it to any pair of non-mechanical quantities and proposed a more generalized classical entropic uncertainty relation.[16,17] Subsequently, Maassen, Uffink, and Kraus improved Deutsch’s result to[18]

The investigation of the entropic uncertainty principle is a hot topic in quantum optics and quantum information. Recently, important advances on the entropic uncertainty principle have been made internationally. One of them is the quantum-memory-assisted entropic uncertainty relation (QMA EUR) proposed by Berta et al.,[19,20] i.e.,

At present, many researchers have studied the relation between quantum correlation, quantum coherence, and entropic uncertainty, and some quantum operations of quantum states are proposed for stable systems, quantum correlation of protection systems, and the reduction of entropic uncertainty,[23–29] for example, the behavior of quantum-memory assisted entropic uncertainty under different noises, and the relations between the quantum-memory-assisted entropic uncertainty principle with teleportation and entanglement witnessed,[30] and influence of quantum discord and classical correlation on the entropic uncertainty in the presence of quantum memory.[31]
It is well known that any environment can be classified as Markovian without the memory effect or non-Markvian with the memory effect. In fact, the realistic environment is strictly the non-Markvian type, and the Markvian environment is just an approximate result in most cases, i.e., in the case of weak coupling, the correlation time of the environment is far less than the associated relaxation time of the system itself. With the development of the experimental technology and the realistic demand of the quantum information technology, the strong coupling between subsystems and the environment has become more and more common in quantum state engineering, e.g., cavity QED system under strong coupling. In this case, the memory of the environment cannot be ignored; the feedback function of the environment on the system must be taken into account. Therefore, the investigation about the quantum system in the non-Markovian environment has important theoretical and practical significance for quantum information processing.
The characterization of non-Markovianity and the advantages of the memory effect is an active field of research.[32–35] Recently, Feng et al. found that the unit noises increase the amount of uncertainty in the Markovian environment.[36] The entropy uncertainty relation in the non-Markovian dissipative environment was investigated in Ref. [37]. In addition, some attention has been paid to the quantum entropic uncertainty of the system by weak measurement and measurement reversal.[38,39]
An interesting question is when two qubits are in different dissipation channels, which qubit should we choose as the quantum register to get better measurement accuracy? Under different choices, what are the dynamical features of quantum coherence, quantum entanglement, and quantum discord used as quantum resources? However, to the best of our knowledge, there has been no report on these questions in the literature. In this paper, the influence of different placement positions of the quantum register is analyzed in detail on the dynamics of quantum coherence, quantum entanglement, and quantum discord. The research results show that the quantum register should be placed in the channel of the non-Markovian effect. This option is beneficial to reducing the entropic uncertainty and its lower bound. The results also show that quantum discord can play a key role in reducing the uncertainty of quantum systems.
The paper is organized as follows. In Section
We consider a system formed by two parts without interaction. Each part consists of a qubit A (or B) that is locally interacting respectively with a dissipative channel RA (or RB). The qubits A and B are initially entangled. Obviously, the model is governed by the following Hamiltonian:[40]

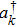

When the environment is at zero-temperature and the qubit is initially in a general composite state of its two levels, the single-qubit reduced density matrix ρ(t) in the qubit basis {|0⟩,|1⟩} has the form




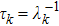

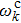
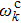

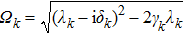
The evolution of the reduced density matrix elements for a single qubit can be easily extended to the two-qubit system. Following the procedure presented in Ref. [43], we find that in the standard product basis {|00⟩ |01⟩ |10⟩ |11⟩}, the diagonal elements of the reduced density matrix ρ(t) for the two-qubit system can be written as










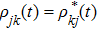
Without loss of generality, in the following simulations, we assume the initial states of the qubits as

In view of the above derivations, we know that the quantum correlation is closely related to the initial quantum state, detuning, channel dissipative effect, and the coupling effect between qubit and channel. Suppose that the observed qubit A and quantum memory qubit B are initially prepared in the X-state, and let A and B independently pass through the noisy channels. For a two-qubit system which is described by the density operator, in the standard computational basis {|00⟩, |01⟩, |10⟩, |11⟩} the density operator can be given by

In order to investigate the properties of the QMA EUR, based on Eq. (


To quantify the entanglement we adopt the concurrence defined by Wootters.[45] In the X-state, the concurrence can be easily calculated by

The coherence of the quantum system is measured by l1-norm standard[46]




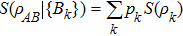






Assume two channels in the studied model are independent, namely, one is a dissipative channel, and the other is a non-dissipative channel. First, we consider the case of the local single dissipative channel. A natural question is which channel should the quantum register be placed in?
The dynamical behavior of the quantum system in the single-sided amplitude damping channel as a function of dimensionless time γt is plotted in Figs.
Notably, from Figs.
Figures
Figures
 | Fig. 5. Dynamics of quantum correlations as a function of the dimensionless quantity γt in ρψ = (r,θ) state with r = 1.0, θ = π/4, and δ = 0.0. (a) λA = λB = 3.0γ. (b) λA = λB = 0.1γ. |
To further study the influence of two-sided amplitude damping channels with different dissipative characteristics on the uncertainty, we assume that one is a non-Markovian channel and the other is a Markovian channel. The coupling strengths between system and environment for two cases are the same γA = γB = γ, but the spectral widths of the noise channel are different, namely, λA ≠ λB.
We perform numerical simulations on the selection of a channel for the quantum register. Comparing Fig.
Figures
 | Fig. 8. Dynamics of correlations as a function of the dimensionless quantity γt in ρψ (r,θ) state with r = 1.0, θ = π/4, and δA = δB = 0.0. (a) λA = 1.0γ, λB = 5.0γ. (b) λA = 5.0γ, λB = 1.0γ. |
The above investigations show that in order to reduce the uncertainty, the quantum register should be placed in the larger non-Markovian channel. In this case, the dynamical process of quantum discord will be changed, but the evolutions of quantum coherence and quantum entanglement will not. These numerical results show that: (i) the uncertainty of the system is closely related to quantum discord, therefore quantum discord plays an important role in reducing the uncertainty of the system; (ii) the quantum register has been placed in the larger degree of the non-Markovianity channel, which is helpful to use the memory effect of the non-Markovian environment, and promotes the loss of quantum information to return to the quantum system from the environment. That is to say, the quantum register in the non-Markovian channel is more likely to play the role of quantum discord resources; (iii) quantum discord is indeed a quantum resource that is different from both quantum coherence and quantum entanglement. The method of maintaining quantum coherence or quantum entanglement is not the same as protecting quantum discord. In some cases, the method of maintaining quantum coherence or quantum entanglement cannot effectively protect quantum discord.
In order to take advantage of the non-Markovian effect, we need to emphasize that in the actual quantum experiment, the non-Markovian dynamics evolution of a qubit (such as qubit B) can be realized by coupling the qubit B with a non-Markovian bath, for example, placing qubit B in photonic band gap materials, or coupling qubit B with an optical cavity of a high quality factor. Furthermore, the control of an environment characterized by non-Markovianity can be achieved by controlling the coupling strength between the qubit and the environment, or by designing a non-Markovian bath (such as a quality factor designed for a good optical cavity).
We investigate how to reduce the uncertainty of the system by optimizing the configuration of the quantum register in the Markovian and non-Markovian channels. The results show that, for the amplitude-damping channel, the uncertainty of the system can be effectively reduced by placing the quantum register in the stronger non-Markovian channel. Moreover, the entropic uncertainty and its lower bound can be reduced by increasing the detuning. The entropic uncertainty is closely related with the quantum discord, which can play a key role in reducing the uncertainty of the system. The increases of detuning and non-Markovian effect are beneficial to protecting the quantum discord and reduce the uncertainty of the system.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] |








