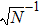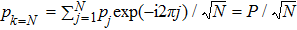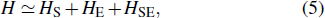1. IntroductionQuantum superposition lies in the heart of both quantum mechanics[1,2] and the current quantum technologies such as quantum communication and computation.[3,4] Any superposition of different states whose evolution is governed by Schrödinger’s equation[5] still satisfies the same evolution equation and remains valid in the quantum world. Upon one measurement, Born’s rule determines the probability of one definite outcome.[6] Another feature of interest in quantum mechanics is the quantum coherence, which is depicted by superposition. For instance, the fringes in the interference experiment of electrons show the coherence of the electron state in different paths. However, interaction between a physical system with its environment may ruin this coherence. This environment-induced process, known as decoherence or dissipation,[7] destroys the coherence of the system, i.e., suppresses strongly the interference of states of the system or dissipates its energy, and singles out a set of states which behave like classical states.[8,9] In the quantum theory of measurement where the system, apparatus, and environment are all treated as quantum objects (governed by Schrodinger’s equation), decoherence is proposed to interpret the outcome of measurements without the collapse of wave packets.[9,10] A number of models of environments which do not dissipate energy of the system but contribute to its decoherence have been studied in the past few decades. For example, the environment can be chosen as a ring of spin 1/2,[11,12] a reservoir of harmonic oscillators,[7,13] and many other external environments.[14]
It seems that quantum theory, while tested thoroughly at the microscopic level, is somehow counter-intuitive in the macroscopic domain. In Schrödinger’s well-known gedanken experiment,[15] a cat, which is described as a macroscopic object (MO), is in a superposition state of alive and dead, which has never been observed in the classical world. In our daily life, the cat is either alive or dead with the same chance but not in the superposition state. In fact, decoherence plays an important role in this transition from the quantum world to the classical world.[8,9] In the universe, isolated systems barely exist, especially the MOs, which must interact with environments (with a large scale of degrees of freedom). Generally speaking, the larger the scale of a system, the faster it decoheres.[16]
As we stated above, various interactions will lead to this quantum-classical transition phenomena. In this paper, we focus on its intrinsic origin, which results in the minimum decoherence even in the absence of any usual environments. It has been found that the collective mode of MOs can be coupled with its inner motion modes.[17–19] Carazza has studied the decoherence effect of the collective variable for free quasi-relativistic particles.[19] Nevertheless, for macroscopic objects, a more reasonable scenario should take the interaction between particles into account, since it is the coupling between particles that bound them into a macroscopic object. Recently, Igor Pikovski et al. has also studied decoherence due to gravitational time dilation in 2015.[20] They phenomenologically thought that the internal movement energy of the system can contribute to its total mass, and the center of mass (CM) was coupled to the internal movement due to the general relativistic effect.
In this paper, we revisit the effect of the special relativity on the decoherence of the collective mode of macroscopic objects. We study a ring of relativistic particles with the nearest–neighbouring interaction, and under some transformation we find there exist interactions between the CM and the internal degrees of freedom. Then we look into the decoherence of CM motion after time evolution and obtain the decoherence time  where N is the particle number, ΔE1,2 is the energy difference of two initial states, ω is the coupling strength, and M is the total mass of CM.
where N is the particle number, ΔE1,2 is the energy difference of two initial states, ω is the coupling strength, and M is the total mass of CM.
The remainder of this paper is organized as follows. In Section 2, we describe the relativistic macroscopic system consisting of N particles and obtain its effective Hamiltonian with the lowest relativistic effect to depict the decoherence of CM motion. In the decoherence dynamics, we choose the initial state as a product state of the superposition states of CM momentum (coherent states) and ground states of simple oscillators, and figure out the time evolution of this state. Then we obtain the reduced density matrix and analyze its decoherence. In Section 3, we study the decoherence of free particles with the same initial state and compare it with the outcomes in Section 2. The conclusions and discussions are in Section 4.
2. The quasi-relativistic macroscopic object2.1. The Hamiltonian of the macroscopic particle ringIn this section, we start from a relativistic MO composed of N particles, each of which obeys the Dirac equation, with the nearest-neighbouring interaction being considered. In special relativistic quantum theory, the Dirac Hamiltonian of a free fermion reads [?]

where
p and
m are the momentum operator and mass of the particle respectively, and

are the Dirac matrices and
c denotes the light velocity. It is well known that there are four eigenvectors where two correspond to positive energy

and the others correspond to negative energy

. In other words, one can diagonalize this Hamiltonian in a block with a unitary transformation
U = exp[
βα ·
parctan(
p/
mc)/2
p] (Ref. [
22]) as

, i.e.,

The positive and negative energy spaces are separated. In the following we will focus on the positive energy part and consider the lowest-order relativistic correction of non-relativistic particles. Actually, the above argument is carried out for Dirac particles. For scalar particles, one can also obtain the mass-energy relation with the Klein–Gordon equation.
Thus the total Hamiltonian of the relativistic MO is

where
m is the mass of a single particle,
pi and
xi are the momentum and position operator at site
i respectively as we set the lattice distance
a = 1. The Hamiltonian to the second-order approximation, which contains the lowest-order term with the relativistic effect, becomes

For simplicity, we choose N as an odd number without loss of generality and take the Fourier transformation

to get the normal modes with
pk and
xk, the momentum and position operators at momentum space respectively. It is worth mentioning that
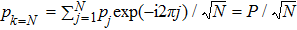
, and

are the momentum and position operators of the CM. That is to say, the
N-th mode describes the motion of CM while the other
N − 1 modes describe the internal relative motion. Therefore, we introduce the CM and relative coordinates in the relativistic Hamiltonian by this Fourier transformation. In this center of mass reference frame, the Hamiltonian in the low-energy limit becomes,

where
δk1 + k2 + k3, qN for
q being one of nonzero integers, is the Kronecker Delta function. It can be seen in Eq. (
4) that the first two terms describe the Hamiltonian of CM while the third and fourth terms describe the relative motions. Obviously the last three terms characterize the interaction between CM and relative motion and the higher order correction.
We then treat the CM system as the “system” and the relative motion system as the “internal environment”. Therefore, this division of the Hamiltonian in Eq. (4) implies that the motion of the system will be influenced by the environment. As a consequence
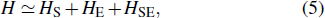
where

where the high order collective terms are neglected. It can be checked immediately that [
HS,
HSE] = 0 and [
HE,
HSE] ≠ 0, which means that evolution governed by the Hamiltonian in Eq. (
5) may cause entanglement between the system and the environment. According to the decoherence theory, this kind of interaction will induce a transition from the quantum superposition state to the classical statistical mixture in the system without energy dissipation.
[7,8]We have obtained the decoherence model, but there remains another problem: different modes of relative motions are not independent but coupled in pairs. We then introduce the Bogoliubov transformation. This transformation is given by (Qk = 1 Qk = 2 ... Qk = N − 1)T = W(N − 1)×(N−1) (qk = 1 qk = 2 ... qk = N − 1)T, where Q stands for P,X, which are the momentums and the displacements of the N − 1 independent relative motions, q for p,x respectively. The transformation W is

For
j ∈ [1,
N − 1], only two elements are non-vanishing in every row and column of
W. Especially,

when
j∈ [1,(
N − 1)/2] and

when
j ∈ [(
N + 1)/2,
N − 1]. We can check that
W ·
W† =
I(N − 1)×(N − 1), and

Finally, the diagonalized Hamiltonian becomes (
ωk = 2
ω sin(
πk/
N))

Now we know that there is only the kinetic term in the system Hamiltonian, the environment contains
N − 1 modes of a simple harmonic oscillator with
N − 1 eigenfrequencies and the motion of CM couples with all the relative motion modes.
2.2. Decoherence dynamicsIn the previous subsection, we obtained the Hamiltonian of the decoherence shown in Eq. (8). With the interaction between system and environment, the evolution equation of the reduced density matrix of the system is the quantum master equation, which is not unitary due to the interaction with its environment.[7] According to Born’s rule, the diagonal terms of the reduced density matrix describe the probabilities of getting some outcome in one measurement, while the off-diagonal ones characterize the interference of different quantum states and show the coherence properties of this system. When the coherence of the system decays with time while the probability terms remain stable, the system undergoes a transition from quantum to classical, i.e., decoherence.[9,16]
We can see that, in the Hamiltonian (8), the relative motions are N − 1 simple harmonic oscillations and the minimal energy difference between two neighbouring levels in the large N limit is 2ħωπ/N. Assuming the temperature of the environment is too low to excite the relative mode, i.e., 2ħωπ/N ≫ kBT, all the relative motions stay in the ground state. Then we choose the initial state as  where |Pi⟩ (i = 1,2) is the eigenstate of P with eigenvalue Pi and |0⟩k is the ground state of the k-th mode of the relative motion Hamiltonian. The total density matrix at time t evolves as
where |Pi⟩ (i = 1,2) is the eigenstate of P with eigenvalue Pi and |0⟩k is the ground state of the k-th mode of the relative motion Hamiltonian. The total density matrix at time t evolves as

The reduced density matrix of the motion of CM is

As |
P1⟩ and |
P2⟩ are the eigenstates of
HS, the diagonal terms of the local (reduced) density matrix in basis |
Pi⟩ are independent of time, i.e.,

. This feature indicates that we are dealing with a pure decoherence process without dissipation. The off-diagonal term reads

where

where
S(
r) is a squeeze operator. Thus the coherence of this system is related with the expectation value of four squeeze operators over the vacuum state (for more details see Appendixes
A and
B). After some calculation, we obtain

where
N0 = (32
M2c4/9(Δ
E1,2)
2), J
n(
x) is the first kind of Bessel function and

. One can conclude from Eq. (
11) that in the large
N limit the decoherence function depends on the scale of the system, the energy difference of initial states, the coupling strength of real particles, and time
t. One may also find that as ω
t ≪ 1, J
0(4
ωt) ≃ 1 − 4
ω2t2, thus the decoherence function becomes

Then the decoherence time (assuming
N ≫
N0) is

In the long time limit,
ωt ≫ 1, J
0(4
ωt) ≃ 0 and

which indicates that only when
N ≫
N0,

, i.e., there is a restriction on the scale of the whole system.
Equations (12) and (13) are the main results of this paper. The decoherence process of CM depends on the scale of the system, the interaction strength of real particles and the difference of the initial kinetic energy. The larger the system is, the faster it decoheres. Table 1 shows a list of decoherence results with respect to systems of different magnitudes (e.g., the universe, the Earth, a person, and C60). For simplicity, we have assumed that all these systems are composed of only carbon atoms. As an example, we consider C60 molecules with coupling strength ω ≃ 1014 Hz. With the two superposed initial velocities of this carbon ring as 200 m/s and 1000 m/s,[23] the lower bound of the particle number is N0 = 1.3×1023 which has the magnitude of Avogadro constant NA = 6.02×1023. Thus no decoherence occurs in a single C60 molecule. Figure 1 shows  as a function of t with different N. First, when N ≪ N0, the off-diagonal element
as a function of t with different N. First, when N ≪ N0, the off-diagonal element  oscillates around 0.48, which means the system barely decoheres; then, as N ≃ N0,
oscillates around 0.48, which means the system barely decoheres; then, as N ≃ N0,  decreases in the beginning and oscillates around 0.25 later, indicating that a portion of coherence is retained in the system; at last, for N ≫ N0, compared with the above two cases,
decreases in the beginning and oscillates around 0.25 later, indicating that a portion of coherence is retained in the system; at last, for N ≫ N0, compared with the above two cases,  decreases to zero immediately thus the state of the CM in this system decoheres. And the decoherence time of this MO is about 10−14 s.
decreases to zero immediately thus the state of the CM in this system decoheres. And the decoherence time of this MO is about 10−14 s.
It is shown in Eq. (11) that the decoherence process depends on  . It seems obscure that when P1 = − P2 the coherence of CM remains unchanged. In fact, this can be seen in Eqs. (4) and (5) that we drop the term
. It seems obscure that when P1 = − P2 the coherence of CM remains unchanged. In fact, this can be seen in Eqs. (4) and (5) that we drop the term  as a higher order term and only keep the one
as a higher order term and only keep the one  . This reduction may be related with our results
. This reduction may be related with our results  . Now it is time to find out the decoherence time as P1 = −P2. In this case, the off-diagonal term of the reduced density matrix is calculated as
. Now it is time to find out the decoherence time as P1 = −P2. In this case, the off-diagonal term of the reduced density matrix is calculated as

where

Here

denotes the term

transformed by
W given in Eq. (
6). Keeping terms up to
t2, one finds

The decoherence times
τ and
τ′ are obtained, which are caused by the
P2 and
P terms of interaction respectively. What is more important,

where
V1(
V2) =
P1(
P2)/
M. Here we know that when
P1 = −
P2, the decoherence effect originates from the interaction term
P with time scale ∼(
V1 −
V2)
2ħω3/32
Mc4. Actually, when

and in the large system limit, we also find that the influence of the
P2 term dominates, i.e.,
τ≪
τ′. In other words, the decoherence process caused by the interaction term
P2 is much faster than the process caused by term
P. This is why we only keep the interaction term
P2 in the very beginning of our paper.
Table 1.
Table 1.
 Table 1. Decoherence time and particle number bound of systems of different scale with coupling strength ω = 1014 Hz. .
|
Universe |
Earth |
Person |
C60 |
| Initial velocity of CM/(m/s) |
2.0×106, 1.0×106 |
3.0×104, 2.0×104 |
10, 5.0 |
1.0×103, 2.0×102 |
| Particle number |
5.0×1078 |
2.5×1050 |
5.0×1027 |
60 |
| Particle number bound |
1.3×1010 |
4.0×1017 |
2.0×1031 |
1.3×1023 |
| Decoherence time/s |
2.0×10−49 |
2.0×10−31 |
3.0×10−13 |
2.4×10−5 |
| Table 1. Decoherence time and particle number bound of systems of different scale with coupling strength ω = 1014 Hz. . |
2.3. Decoherence of cat: Superposition of coherent statesIt is well known that the eigenstates of momentum operators are ideal quantum states, and that they are difficult to prepare in experiments. More “classical” states in quantum mechanics are coherent states, like |α⟩, which are generated by applying the displacement operators on the vacuum states. One important property of the coherent state is that it satisfies the minimum uncertainty relation. Moreover, coherent states behave as Gaussian wave packets in both momentum and position space. In this subsection, we study the decoherence of a more “classical” quantum state, cat state, i.e., the superposition of coherent states. Here the Wigner function in phase space is a useful tool in exploring the non-classicality of quantum states.[24]
Here we consider that the CM is prepared in a macroscopic superposition state ∼|α⟩ + |β⟩ initially, and the relative modes are still in ground states, describing a non-excited internal environment,

where
Ξ is the normalization factor and
α(
β) is a complex number. The reduced density matrix of the motion of CM is

where

As illustrated in Subsection
2.2, the decoherence function relies on the overlap of two quantum states,

. For simplicity, we replace this overlap function with its modulus,

In momentum representation, the coherent state behaves as a Gaussian wave packet with packet width
ħ/2
σ and the mean momentum
ħℑ(
α)/
σ,

At first glance, it seems difficult to deal with the reduced density matrix given in Eq. (
17) as its dimension is infinite. In order to quantify this decoherence process of CM, we introduce the quasi-probability distribution, Wigner function, which is defined as

Although the Wigner function is a real function, it cannot be interpreted as a probability distribution function since it can be negative. Nevertheless, if integrating it over
p (
q), one will get the probability distribution function of
q (
p).
Inserting Eqs. (17) and (18) into Eq. (19), we calculate the Wigner function of the center of mass

where

which are the direct Wigner functions contributed by quantum state |
α⟩ and |
β⟩ respectively, and

is the one caused by the interference term |
α⟩ ⟨
β| + |
β⟩ ⟨
α|, and we have set
Gq(
x)≡
q + 2
σ x and
γ = 9
Nħ4/128
σ4m4c4.
In the beginning, the two direct Wigner functions in phase space are centered at (q = 2σℜ(α), p = ħℑ(α)/σ) and (q = 2σℜ(β), p = ħℑ(β)/σ) respectively, which are exactly the mean position and momentum of two coherent states, while the interference one is approximately centered at (q = σ(ℜ(α) + ℜ(β)),p = ħ(ℑ(α) + ℑ(β))/2σ) (the midpoint of the centers of the two direct terms). Figure 2(a) shows the Wigner function in phase space at t = 0, where two packets correspond to the two coherent states and the oscillations correspond to the interference term. Since p stands for the momentum of the whole system (center of mass), p/N indicates the mean momentum of a single particle. In this case, the two packets are centered at (p/N = 0.3, q = 10) and (p/N = 0.7,q = 6) respectively. This raises the following question: How does the total Wigner function evolve with time?
First, let us turn to a mathematical function Ω(x, y) = exp[−x2 − 2(ay − b)2 − dy2(1 − 2x2)] where a > 0,d ≥ 0. One can prove that if 2a2 ≫ d and a2 > 2b2d, the position of its peak is x = 0,y = b/a, Ω(x,y)|peak = Ω(x = 0, y = b/a) = exp[−db2/a2]. Then in our occasion, if 2γ(1 − J0(4 ωt)) ≪ N4, 8γ(1 − J0(4 ωt))ℑ(α)2 < N4, and 8γ(1−J0(4ωt))ℑ(β)2 < N4 (our choice mentioned above meets all these conditions), the positions of the peaks of three Wigner functions terms remain unchanged with time (as shown in Fig. 2)

It is depicted by the above equation that the peak value of the three Wigner function terms is at time
t. Since the two direct terms describe the probability distributions of two coherent states respectively and the oscillation term describes the interference effect, it sounds reasonable to quantify the decoherence of the superposition of coherent states with the peak values of the Wigner function. A useful quantity introduced by Zurek
[24] is the fringe visibility function

Obviously, the fringe visibility function describes the decay of the peak value of the interference term. In other words, it shows the decoherence of the system, which originates from its interaction with the environment. Here, the fringe visibility function gives

When expanded at the small time and large time limit, the above equation becomes

where

is the new particle number restriction, Δ
Eα,β =
ħ2(ℑ(
α)
2 − ℑ(
β)
2)/2
Mσ2 is the difference of mean kinetic energy of the two coherent states. Figure
2 shows the time evolution of the Wigner function. When
t < 1/
ω the interference term is damped over time while when
ω t = 100≫1, a portion of coherence still remains. Figure
3 shows the Wigner function at the large time limit with different
N while the centers of the two direct terms remain unchanged. It is shown that the larger the particle number
N is, the less coherence it keeps in the large time limit. All these features coincide with the analysis results given in Eq. (
24). Now we obtain the decoherence function of a macroscopic superposition quantum state, ∼|
α⟩ + |
β⟩, which depends on the mean momentum of the two superposed coherent states
ħℑ(
α)/
σ and
ħℑ(
β)/
σ. What is more, this function
F(
α,
β,
t) is highly similar to the result we get in Subsection
2.2,

where △
E1,2 is the difference of the kinetic energy of the two superposed states. Similar to the outcome in Subsection
2.2, in the superposition of the coherent states case, the decoherence time depends on the scale of the total system, the interaction strength of real particles, and the difference of the initial kinetic energy.
3. Free-particles evolutionIn Subsection 2, we studied the decoherence of the CM in a ring with N relativistic particles with the nearest-neighbouring interaction and find that a restriction on particle number is necessary for the decoherence of CM. Next, we will explore whether or not this particle number restriction is induced by the nearest-neighbouring interaction. To this end, in this section, we investigate the system of N free relativistic particles

We point out that the results about the cases without inter-coupling could not be simply achieved from the above consequence by asumming the couplings vanish.
Making the Fourier and Bogoliubov transformations mentioned above in Eqs. (3) and (6), one finds this Hamiltonian, to the second order approximation, becomes

where
P describes the momentum of CM and
Pk the momentum of the
k-th mode of relative motion.
As there are only momentum terms in Eq. (26), the three terms commute pairwise. Therefore, for an initial state such as the product state of the collective and relative momentum operators, no decoherence will occur. What is more, in Section 2 the initial state of the kth mode relative motion is chosen to be the ground state of the simple harmonic oscillator, which in position representation behaves as the Gaussian wave packet with width ħ/(4mω sin(π/N)k). To make sure that the two models start from the same condition, we set the initial state of the free-particle model as

where

is a Gaussian wave packet with packet width

. As the evolution of the state is governed by Eq. (
26), the state at time
t reads

where

. Then the off-diagonal element of the reduced density matrix becomes

For small
t, we obtain

with decoherence time

Comparing these two model, we find that with the same initial state the CM decoheres at the same rate as the outcome we obtained in Section
2, while there is no restriction on the particle number (
N0) in the free-particle model. This finding concludes that the restriction is introduced by the nearest-neighboring interaction between relativistic particles in the ring. In fact, this product state in the collective and relative movement reference frame corresponds to an entanglement state in the real-particle movements frame. Moreover, this entanglement state is difficult to prepare in experiments since particles are all free. By the way, the transformation between the two frames considered in this paper is