Project supported by the National Science Fund for Outstanding Young Scholars of China (Grant No. 11722548) and the National Natural Science Foundation of China (Grant Nos. 11574339 and 11404361).
Project supported by the National Science Fund for Outstanding Young Scholars of China (Grant No. 11722548) and the National Natural Science Foundation of China (Grant Nos. 11574339 and 11404361).
† Corresponding author. E-mail:
Project supported by the National Science Fund for Outstanding Young Scholars of China (Grant No. 11722548) and the National Natural Science Foundation of China (Grant Nos. 11574339 and 11404361).
Carbon nanotubes (CNTs) have long been expected to be excellent nanochannels for use in desalination membranes and other bio-inspired human-made channels owing to their experimentally confirmed ultrafast water flow and theoretically predicted ion rejection. The correct classical force field potential for the interactions between cations and CNTs plays a crucial role in understanding the transport behaviors of ions near and inside the CNT, which is key to these expectations. Here, using density functional theory calculations, we provide classical force field potentials for the interactions of Na+/hydrated Na+ with (7,7), (8,8), (9,9), and (10,10)-type CNTs. These potentials can be directly used in current popular classical software such as nanoscale molecular dynamics (NAMD) by employing the tclBC interface. By incorporating the potential of hydrated cation-π interactions to classical all-atom force fields, we show that the ions will move inside the CNT and accumulate, which will block the water flow in wide CNTs. This blockage of water flow in wide CNTs is consistent with recent experimental observations. These results will be helpful for the understanding and design of desalination membranes, new types of nanofluidic channels, nanosensors, and nanoreactors based on CNT platforms.
A nanotube that enables fast water flow while rejecting ions is of great importance in water desalination and purification,[1–6] nanofluidics manipulation,[7–12] ion detection,[13] drug delivery,[14,15] nanodevice fabrication,[16–21] and biomimetic membrane pore design.[22,23] It has been found that carbon nanotubes (CNTs) have an extra high water flow rate from theoretical simulations[24–28] and experimental observations.[29,30] In 2001, Hummer et al.[24] theoretically predicted the potential effectiveness of water flow in nanotubes using a molecular dynamics (MD) simulation, and in 2006, Holt et al.[30] experimentally demonstrated that the water permeability of CNT-based membranes is several orders of magnitude higher than that expected from conventional hydrodynamic theories. Using classical MD simulations based on traditional force fields, it has been theoretically shown that narrower CNTs, with diameters smaller than the size of hydrated ions, would reject the passage of ions while still maintaining ultrahigh permeability for the water flow; an example is a (6,6)-type CNT with a diameter of ∼ 0.5 nm.[25,31]
With the benefit of this unique property of fast water flow combined with ion rejection, narrower CNTs have been expected to be good candidates for water desalination and purification channels for a decade.[31,32] However, to date, there has been insufficient experimental demonstration of salt rejection adequate for desalination using pristine CNTs.[2] Moreover, for wide CNTs (inner diameter above 1 nm), several experiments[33–35] have shown that there is only very, and even negligibly, small water flow and ion permeation across the CNTs without the addition of pressure or electric field above a threshold. In contrast, results based on popular classical MD simulations showed that there should be fast water permeation across wider tubes.[31] One of the main reasons is the lack of a correct classical force field potential for the interactions between cations and different CNTs, which results in an incomplete understanding of the transport behaviors of ions near and inside the CNT.
Recently, by incorporating the cation-π interaction potential[3] to classical all-atom force fields, we found that cations block water flow through narrow (6,6)-type CNTs due to interactions between cations and aromatic rings in CNTs. In wide CNTs (8,8), these interactions trap the cations in the interior of the CNT, inducing unexpected open or closed state switching of ion transfer under a strong electric field, which is consistent with experiments. More appropriate classical force field potentials for the interactions between cations and other CNTs are expected to enable better understanding of the solution transport behaviors of ions near and inside CNTs. Here, we provide classical force field potentials for the interactions of Na+/hydrated Na+ with (7,7), (8,8), (9,9), and (10,10)-type CNTs using density functional theory (DFT) calculations, which can be directly used in current popular classical software such as nanoscale molecular dynamics (NAMD) by employing the tclBC interface. For an (8,8)-type CNT, compared to our previous potential,[3] we provide a more accurate classical force field potential for the interactions of Na+/hydrated Na+ adsorbing inside an (8,8)-type CNT. This will facilitate further CNT-based research and applications.
We built four armchair CNT clusters with different curvatures: (7,7), (8,8), (9,9), and (10,10), corresponding to molecular formulas C168H28, C192H32, C216H36, and C240H40, respectively. All their entrances were passivated by H atoms. The lengths of the (7,7), (8,8), (9,9), and (10,10)-type CNTs (along the tube axis, defined as the Z axis) were approximately 15.4 Å. They contained five aromatic rings, and both ends had H atoms attached. Their diameters were 9.6 Å, 10.9 Å, 12.3 Å, and 13.6 Å after DFT optimization.
The original configurations of the (7,7), (8,8), (9,9), and (10,10)-type CNTs were derived from the visual package visual molecular dynamics (VMD).[36] First, the atoms of the four CNT models were freely optimized to obtain the most stable CNT structures, shown in Fig. 

In our previous work,[3] we provided the classical force field potentials for the interactions of Na+/hydrated Na+ with (6,6) and (8,8)-type CNTs by simply scanning the interaction energies along the central axis of the tubes using DFT calculations. This method is relatively rough for wide tubes such as (8,8)-type CNTs since the most stable cation adsorption sites are not always in the central axis of the tube. In this work, we provide more accurate potentials for Na+/hydrated Na+ inside wide tubes. First, we optimized the geometric structures for Na+ ions in the center (the point along the Z axis defined as the original point, Z = 0 Å) and at the entrance (Z = 7.8 Å) of (7,7), (8,8), (9,9), and (10,10)-type CNTs. We note that there are three different types of site inside CNTs. We investigated the most stable Na+ structure in a (7,7)-type CNT in PS1 of the ESI. We obtained results similar to our previous study,[40] which are that the H site is the most stable, the B sites are sub-stable, and the T site is unstable, where the Na+ ion moves to the H site during geometry optimization. The most stable structures of the system using (7,7)-type CNTs as examples are shown in Figs.
 |
These adsorption energies are shown in Fig.
Hydrated Na+ combined with six water molecules adsorbed in (7,7), (8,8), (9,9), and (10,10)-type CNTs was investigated, with the corresponding adsorption sites at Z = 0 Å and Z = 7.8 Å. When comparing with Na+ at the H site, B site, and T site, we found the H site is also the most stable for hydrated Na+ in (7,7)-type CNTs. The geometric structures and the adsorption energies are shown in PS4 of the ESI. We also investigated the different hydrated Na+ conformers to find the most stable conformer at the H site in PS5 of the ESI. Examples of the most stable structures of the system for (7,7)-type CNTs are shown in Figs.
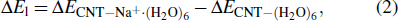 |
 |
From Fig.
Moving the Na+ ion along the inner wall with fixed Z coordinate while freely varying the X and Y coordinates can reveal the most stable points of adsorption energies between Na+ and CNTs with Z ranging from Z = 0 Å to Z = ± 10.2 Å. Fitting these points as curves can reveal the classical force field potential for the interactions between Na+ and CNTs. The curve fits, shown in Fig.
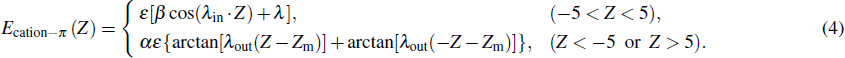 |
 | Fig. 4. (color online) (a)–(d) Adsorption energies and curve fits for Na+ with (7,7), (8,8), (9,9), and (10,10)-type CNTs, respectively. |
The seven parameters of the classical force field potential curves for the interactions between Na+ and (7,7), (8,8), (9,9), and (10,10)-type CNTs are shown in Table
| Table 1.
Seven parameters from fitting the potential energy curves of Na+ ion in CNT systems of different curvatures. . |
We use a (9,9)-type CNT as an example. By incorporating the cation-π interaction potential in a classical all-atom force field using the tclBC code (the details of the tclBC code for (7,7), (8,8), (9,9), and (10,10)-type CNTs are shown in PS7 of the ESI), we perform a simulation using a filter membrane containing four (9,9)-type CNTs, as shown in Fig.
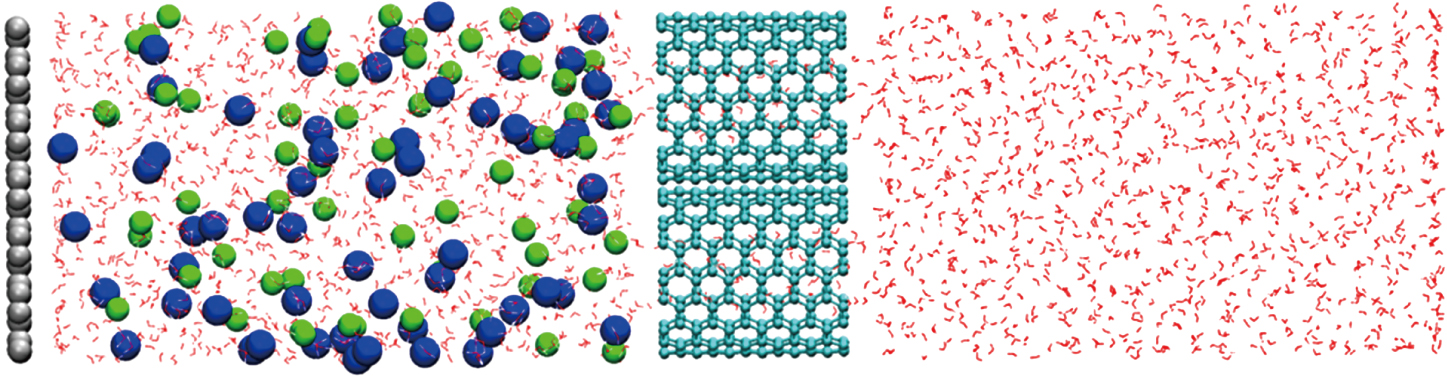 | Fig. 5. (color online) Initial carbon nanotube (CNT) filter membrane system containing four (9,9)-type CNTs segregating the NaCl solution and pure water. |
Figure
We investigated the adsorption energies of Na+/hydrated Na+ with (7,7), (8,8), (9,9), and (10,10)-type CNTs in the center and at the entrance using DFT calculations. The results show the interaction between Na+ with CNTs is quite strong, over 42 kcal/mol in the center and over 27 kcal/mol at the entrance of the CNTs. Although the adsorption energies of hydrated Na+ with these CNTs are reduced to about half that of Na+, they remain approximately three times stronger than the hydrogen binding energy in two water molecules at the same temperature.
By scanning the adsorption energies from the inside to the outside of these CNTs and by utilizing the cosine function in conjunction with paired arctan functions, we found the potential curve can be described well by fitting Eq. (
By incorporating the hydrated cation-π interaction potential obtained here to classical all-atom force fields, we showed that the ions will move inside the CNT and accumulate there. This will block water flow through wide CNTs, which is consistent with recent experimental observations. Our results will help in water desalination and purification, nanofluidic manipulation applications, and other aspects based on the CNT platform.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] |





