Project supported by the National Key R&D Program of China (Grant No. 2017YFA0303203) and the National Natural Science Foundation of China (Grant No. 11474149).
Project supported by the National Key R&D Program of China (Grant No. 2017YFA0303203) and the National Natural Science Foundation of China (Grant No. 11474149).
† Corresponding author. E-mail:
Project supported by the National Key R&D Program of China (Grant No. 2017YFA0303203) and the National Natural Science Foundation of China (Grant No. 11474149).
The Andreev-like levels and the free energy of the spin superconductor/insulator/spin superconductor junction are obtained by using the Bogoliubov–de Gennes equation. The phase dependence of the spin supercurrents exhibits a 0–π transition by changing the barrier strength. The dependences of the critical current on the barrier strength and the temperature are also presented.
In the conventional superconductor, the electrons are condensed into the Cooper pairs, forming a Bardeen–Cooper–Schrieffer (BCS) ground state.[1] Each Cooper pair carries two units of the electron charge and no spin polarization for spin-singlet pairing. Being the counterpart of the charge superconductor, there also exists a quantum state, called a spin superconductor (SSC), where the condensed pair is composed of an electron and a hole rather than two electrons.[2–5] The electronlike spin-up carriers and the holelike spin-up carriers attract each other due to the Coulomb interaction[6] and form the Cooper pairs in the SSC, which are the charge neutral spin-triplet pairs carrying two units of the electron spin. About four decades ago,[7,8] electron–hole Cooper pairs were predicted in a double-layer system, where the electron in one layer and the hole in the other layer are separated by an insulator. The insulating layer is proposed to be thin enough to allow for the strong Coulomb interaction between the electrons and the holes leading to an effective attraction but thick enough to prevent the electron–hole recombination. Experimentally, the existence of the exciton condensate in the semiconductor double quantum well systems was also reported.[9,10] In addition, the spin superconductivity can exist in various systems, such as the spin-polarized triplet exciton systems of graphene,[2,3] Bose–Einstein condensate of magnetic atoms,[11–13] Bose–Einstein condensate of magnons and spinons,[14–16] and so on. Very recently, the signature of spin superconductivity has also been observed experimentally in canted antiferromagnet Cr2O3.[17]
The conventional Josephson effect is the phenomenon of the supercurrent across a device known as the Josephson junction, which consists of two superconductors coupled by a weak link.[18–23] The charge supercurrent across the junction is mediated by the Andreev bound states formed by the electrons and holes inside the normal segment of the junction.[24–31] As an analogy of the conventional Josephson junction, the SSC Josephson junction can be achieved by a weak link between two SSCs. There are both the spin-conserved and the spin-flip reflections at the normal-metal/SSC interface,[3] which are the counterparts of the normal reflection and the Andreev reflection at the normal-metal/superconductor interface, respectively. The repeated spin-flip reflections in the SSC Josephson junction, just like the Andreev reflection in the conventional Josephson junction, will lead to the formation of Andreev-like bound states and a dissipationless pure spin current.[32]
In this paper, we investigate an SSC Josephson junction by employing the Bogoliubov–de Gennes (BdG) approach, which is completely in parallel to the treatment in the conventional Josephson junction. The Andreev-like levels and the free energy of the junction are obtained. It is shown that there is a pure spin supercurrent driven by the phase difference of the junction. The current phase relation can exhibit a 0–π transition by tuning the barrier strength. We note that there are two differences between the SSC Josephson junction and the conventional one. First, the supercurrent in the SSC Josephson junction is a pure spin current rather than a charge current. Second, the 0–π transition is tuned by the barrier strength rather than the magnetic middle layer.[33–36] The dependences of the critical current on the barrier strength and the temperature are also discussed.
The rest of this paper is organized as follows. The formalism is presented in Section
The model under consideration is a one-dimensional junction oriented along the x axis. The junction consists of two SSCs sandwiched by an insulating layer at x = 0. The SSC can be described by a minimal two-band model,[6] where an electron in the spin-up conduction band and a hole in the spin-down valence band can be condensed into a Cooper pair due to the Coulomb interaction. Both the electrons in the spin-up band and the holes in the spin-down band possess the spin of +ħ/2, thus the Cooper pair is charge neutral and has a spin of ħ. The dispersion of the spin-up conduction band and that of the spin-down valence band are assumed as ε+ = p2/2m−M0 and ε− = −p2/2m+M0, respectively, with p being the momentum, m the mass of the electron, and M0 the exchange energy. The spin-down conduction band and the spin-up valence band are far from the Fermi level and are irrelevant to the transport.
In the basis of (ψ+, ψ−)T, with ψ± being the field operators of the electrons in band ε±, the BdG Hamiltonian of the SSC reads
 |
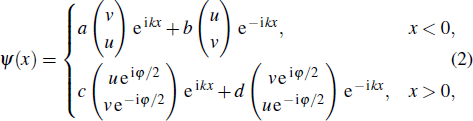 |
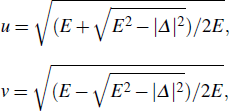 |
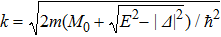
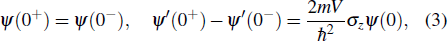 |
The Pauli matrix in Eq. (
Boundary conditions (
 |
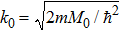
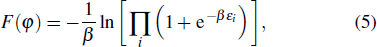 |
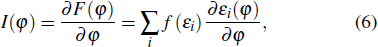 |
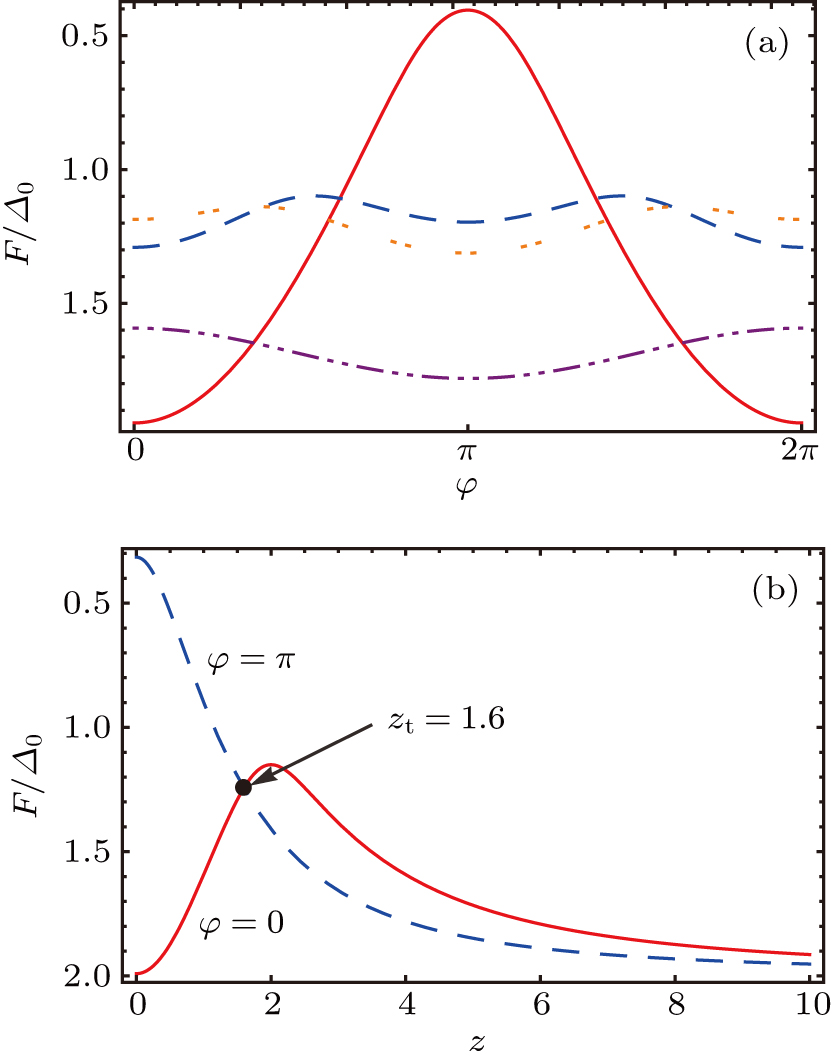
The free energy of the junction is plotted in Fig.
The 0–π transition point zt can be found as the cross point of the curves F(z,φ = 0) and F(z,φ = π) as shown in Fig.
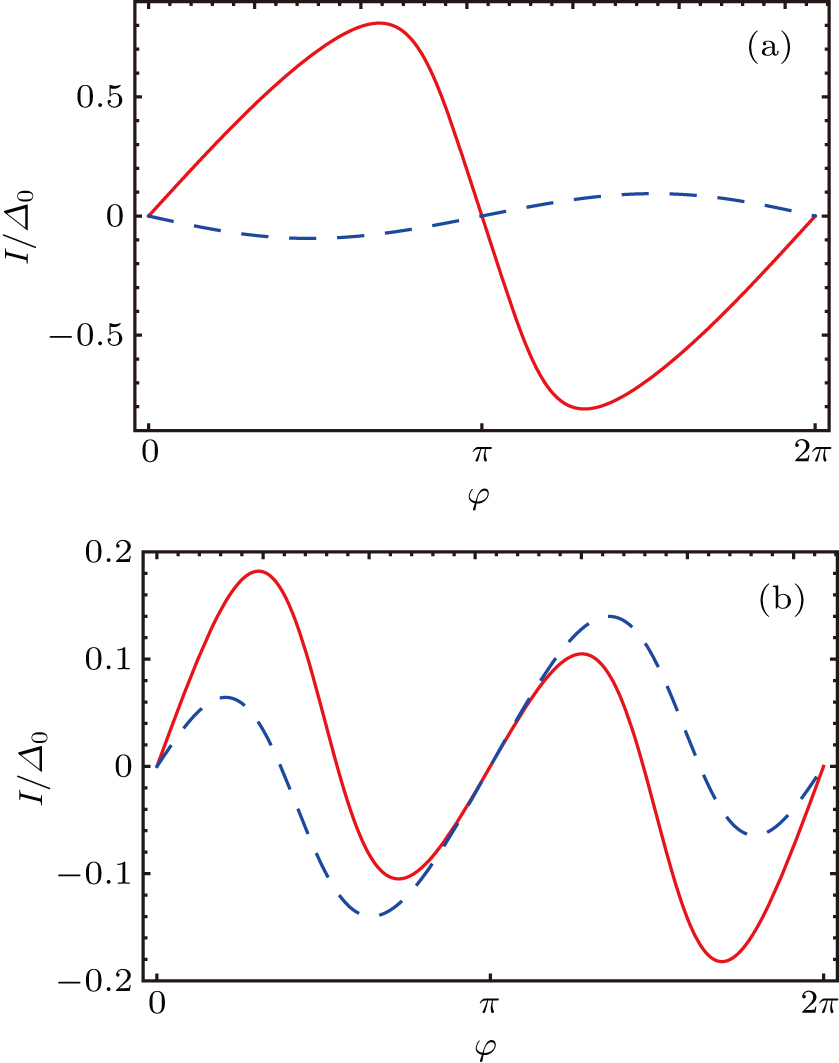
The 0–π transition can also be indicated by the phase dependence of the Josephson spin current, which is depicted in Figs.
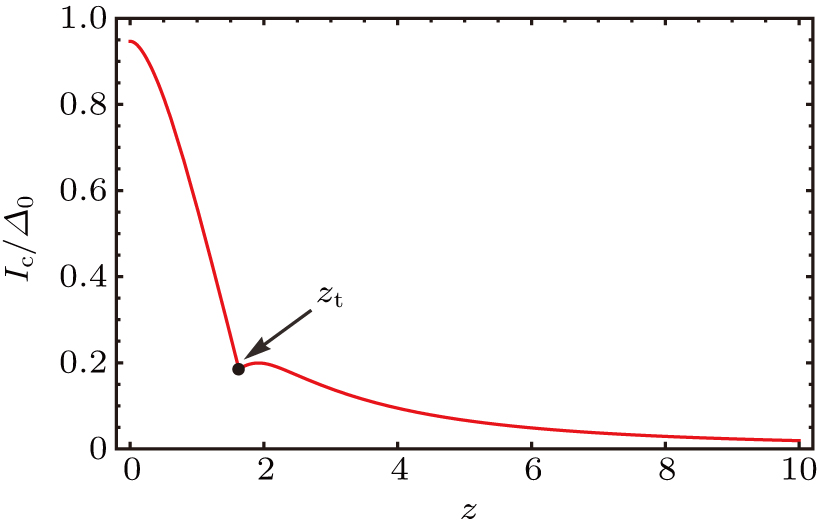
The critical spin current Ic, which is defined as the maximum Josephson spin current, is shown in Fig.
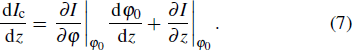 |
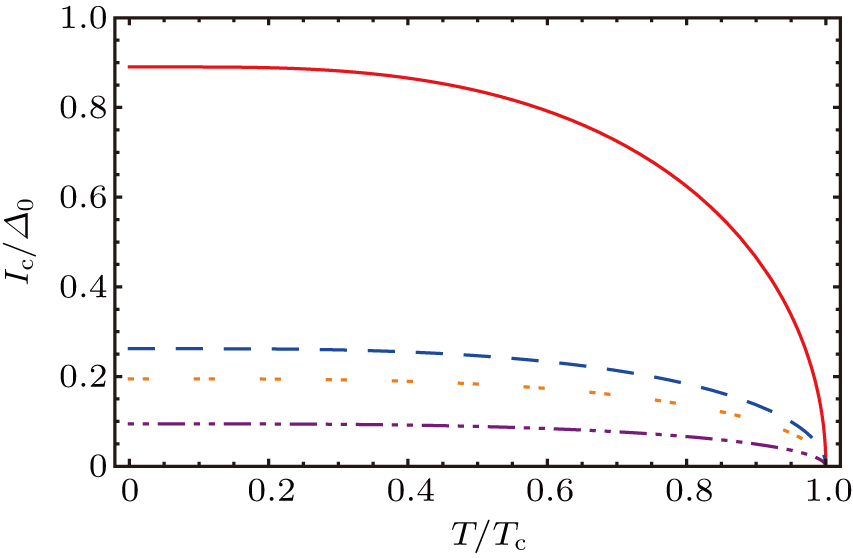
Finally, we present the temperature dependence of Ic in Fig.
We investigate the dc Josephson effect in an SSC Josephson junction. In contrast to the conventional Josephson junction, the Josephson current is a pure spin current and the 0–π transition is driven by the barrier strength rather than the magnetic mechanism. The signals of the 0–π transition are shown in the free energy, in the current-phase relation, and in the critical Josephson current.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |