Cite this Article
Sui Pengfei, Dai Jiaqi, Zhao Yinchang, Dai Zhenhong. Adsorptions of metal adatoms on graphene-like BC3 and their rich electronic properties: A first-principles study. Chinese Physics B, 2018, 27(9): 097311  
Permissions
Adsorptions of metal adatoms on graphene-like BC3 and their rich electronic properties: A first-principles study
Sui Pengfei1, Dai Jiaqi2, Zhao Yinchang1, Dai Zhenhong1, †
Department of Physics, Yantai University, Yantai 264005, China
Department of Physics, Renmin University of China, Beijing 100872, China

 

† Corresponding author. E-mail: zhdai@ytu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11774396 and 11704322) and Shandong Natural Science Funds for Doctoral Program, China (Grant No. ZR2017BA017).

Abstract

Density functional calculations have been performed to investigate the adsorption of twenty two different kinds of metal adatoms on graphene-like BC3. In contrast to the graphene adsorbed with adatoms, the BC3 with adatoms shows many interesting properties. (1) The interaction between the metal adatoms and the BC3 sheet is remarkably strong. The Li, Na, K, and Ca possess the binding energies larger than the cohesive energies of their corresponding bulk metals. (2) The Li, Na, and K adatoms form approximately ideal ionic bonds with BC3, while the Be, Mg, and Ca adatoms form ionic bonds with BC3 with slight hybridization of covalent bonds. The Al, Ga, In, Sn, and all transition metal adatoms form covalent bonds with BC3. (3) For all the structures studied, there exhibit metal, half-metal, semiconducting, and spin-semiconducting behaviors. Especially, the BC3 with Co adatom shows a quantum anomalous Hall (QAH) phase with a Chern number of −1 based on local density approximation calculations. (4) For Li, Na, K, Ca, Ga, In, Sn, Ti, V, Cr, Ni, Pd, and Pt, there exists a trend that the adatom species with lower ionization potential have lower work function. Our results indicate the potential applications of functionalization of BC3 with metal adatoms.

PACS: 73.22.-f;68.43.Bc;73.20.Hb
Keyword:density functional theory;metal adatoms;graphene-like BC sheet;anomalous Hall conductivity
1. Introduction

Graphene, a two-dimensional honeycomb lattice of carbon, has stimulated a large number of research activities since its experimental realization.[1] So far, many exceptional features, such as the high strength of the lattice structure, massless Dirac fermions, the high thermal conductivity, and the half-integer Hall conductance, have been revealed for this atomically thin layer.[2–5] To modify the electronic properties of graphene, recent investigations have confirmed some chemical functionalized graphene structures like graphane,[6–10] grapheneoxide,[11–13] fluorographene,[14–18] etc. Meanwhile, the adsorption of metal atoms is also used to change electronic structures to enhance the applications of graphene. For instance, the adsorption of alkali and alkali-earth metal adatoms can dope electrons to graphene, resulting in a down-shift of the Dirac point;[19] metal-coated graphene possesses considerable hydrogen storage capacity;[20–22] lithium decorated graphene shows conventional superconductivity;[23] the graphene with 5d transition metal adatoms presents quantum anomalous Hall (QAH) effect,[24] etc. However, the binding energies (Eb) between the metal atoms and graphene are lower than the cohesive energies (Ec) of the corresponding bulk metals,[19,25,26] which implies that the clustering of the adatoms is inevitable. In order to increase Eb, it is proposed to substitute the carbon atoms in graphene with some metal atoms.[27] Nonetheless, the substitution of carbon atoms with metal atoms creates vacancies and damages the structure of graphene severely.[28]

It was reported that the boron doped carbon nanostructures could suppress the clustering of metal adatoms.[29–32] Most strikingly, at the same time of the production of graphene,[1] the BC3 honeycomb sheet was also realized experimentally.[33,34] Different from graphene, the hexagonal BC3 sheet is a semiconductor due to the lack of dangling bonds in it. For hydrogen storage, this two-dimensional (2D) BC3 sheet has been predicted as one of the most promising host materials because there is no clustering of metal adatoms.[35,36] Recently, the Fermi surface nesting in the BC3 was investigated, revealing that Li coated BC3 can be taken as an experimentally feasible structure for exploring the nesting-driven quantum phases.[37] Furthermore, the topological superconductivity in doped BC3 sheet was also predicted, which provides a promising route toward the realization of a genuine 2D helical p+ip superconductor.[38] Therefore, it is important to systematically investigate the adsorption of metal atoms on the BC3 sheet. In this paper, twenty two different metal adatoms, whose adsorptions on graphene or silicene have been studied,[19,39,40] are used to study their adsorption properties on the BC3 sheet. The binding energy, geometry, density of states (DOS), dipole moment, charge transfer, and work function of each adadatom–BC3 structure are calculated. The calculation details are described in Section 2. The results on structural and electronic properties of metal adatom on BC3 are presented in Section 3. Section 4 is the summary.

2. Method

The spin-polarized density functional theory (DFT) is employed in our calculations by using the Vienna ab initio simulation package (VASP) code.[41] The projector augmented-wave (PAW) method[42] is adopted with an energy cutoff of 520 eV. The generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE)[43] exchange correlation energy is used. For the pristine BC3 unit cell, in which there are two boron atoms and six carbon atoms, we use the Brillouin zone (BZ) samplings with 12 × 12 × 1, 18 × 18 × 1, and 36 × 36 × 1 Monkhorst–Pack grids[44] for relaxations, static calculations, and density of state calculations, respectively. The Monkhorst–Pack grid for a BC3 supercell is chosen to be inversely proportional to the dimensions of the supercell. The vacuum space along the z direction is larger than 15 Å. The tolerance for the energy convergence is 10−5 eV and all structures are fully relaxed until the force on each atom is smaller than 0.01 eV/Å. The dipole corrections implemented in VASP code[45,46] are applied to potentials and total energies in all systems to remove the spurious dipole interactions between the periodic images.

3. Results and discussion

The bond lengths of B–C and C–C bonds in the BC3 sheet are 1.56 Å and 1.42 Å, respectively, which is consistent with the previous work.[47,48] The lattice constant of BC3 unit cell is 5.17 Å which is larger than twice of that of graphene due to the existence of the B–C bonds. The electronic structure shown in Fig. 1 indicates that the energy gap of pristine BC3 is 0.66 eV. The Dirac state is 2.4 eV above the Fermi level. The maximum valence band (VBM) locates at the Γ point while the minimum conduction band (CBM) is at M point. Figure 1 also shows the decomposed charge densities of the VB and CB at other symmetry points. In addition, the work function of the pristine BC3 sheet is 5.52 eV while for graphene it is 4.49 eV.[19] Because the atomic radius of the boron atom is larger than that of carbon atom, this is in contradiction to the general trend that the larger the atomic radius, the smaller the work function, but consistent with the trend found in silicene.[40]

Fig. 1. (color online) The band structure, projected density of states (PDOS), and band decomposed charge densities of VB and CB at the Γ, M, and K symmetry points for pristine BC3 unit cell. The Fermi level is set to be at zero.

A supercell consisting of (2 × 2) BC3 unit cells presented in Fig. 2 is adopted for the calculations of the adsorption of metal atoms on BC3. The distance between the neighboring metal adatoms is 10.35 Å which is larger than 9.88 Å as considered for the 4 × 4 graphene supercell.[19] The K atom has the largest atomic radius among all the adatoms considered. The difference of the binding energy of the K adatom on the (2 × 2) and (3 × 3) BC3 supercells is less than 5 meV. Thus, the interaction between the metal adatoms is so weak that the structures with a metal adatom on the (2 × 2) BC3 supercell can be taken as an approximation of an isolated adatom on BC3. We have considered six different adsorption sites as follows: the hollow site above the center of a carbon hexagon (H1), the hollow site above the center of a boron-carbon hexagon (H2), the top site above a carbon atom (T1), the top site above a boron atom (T2), the bridge site above the center of C–C bond (B1), and the bridge site above the center of B–C bond (B2), as shown in Fig. 2. The binding energy of metal adatoms on BC3 is defined as Eb(M) = E(M) + E(BC3) − E(M–BC3), where E(M), E(BC3), and E(M–BC3) are the energies of an isolated metal atom, the BC3 supercell, and the adatom–BC3 system, respectively. The larger values of Eb represents the stronger binding of the metal adatom to BC3 sheet.

Fig. 2. (color online) Top view and lateral view of the (2 × 2) structure of the hexagonal BC3. The big and the small balls represent the boron and carbon atoms, respectively. Six different adsorption-sites are labeled as H1, H2, T1, T2, B1, and B2.
3.1. Energetic, structural, and electronic properties

For each adatom, the adsorption on the six possible sites are investigated firstly, as shown in Fig. 3. Possible diffusion pathways and the energy barrier of the adatoms on BC3 lattice can be deduced from the binding energy on each site. For example, the diffusion pathway of Li from H1 to H2 sites is H1→B1→H2 and the corresponding energy barrier is 0.41 eV, while the diffusion path between the adjacent H2 sites is H2→B2→H2 with an energy barrier of 0.38 eV. The exact diffusion energy barrier can be calculated using the nudged elastic band (NEB) method.[49] They are about 0.42 eV and 0.39 eV for the above two pathways, which are close to the difference between the Eb’s at the corresponding adsorption sites. In addition, the energy barrier from H2 to H1 is 0.32 eV. Therefore, Li adatoms on the BC3 sheet favor the diffusion path H1→B1→H2→B1→H1 with the largest barrier value of 0.42 eV. Upon full geometry optimization, Li, Na, K, Al, Ti, V, Mo, W, Mn, Fe, and Co favor bondings on the H1 site, while Be, Mg, Ca, Ga, In, Sn, Cr, Ni, Pd, and Pt prefer to adsorb at the H2 site. Exceptionally, Au adatoms prefer adsorbing at the B2 site of BC3.

Fig. 3. (color online) Binding energy of 22 different metal adatoms on six possible adsorption sites of the (2 × 2) BC3 sheet. The data on sites of H1, B1, T1, B2, T2, and H2 are listed from left to right for each adatom studied.
3.1.1. Alkali and alkali-earth metal adatoms

For Li, Na, K, and Ca, the binding energy Eb on any adsorption site is larger than the cohesive energy Ec per atom of the corresponding bulk metal, as shown in Fig. 3 and Table 1. The K adatom on BC3 has the largest ratio of Eb to Ec (Eb/Ec ≈ 2.52) at H1 site, and the corresponding binding energy Eb is about 2.50 eV, which is much larger than 0.86 eV and 2.04 eV of K adatoms on graphene and silicene.[19,39] Mg has the smallest Eb of 0.84 eV among all the adatoms studied. The adatom height h increases with the increase of the atomic radius of adatoms. This interprets the lowest h of Be adatom on BC3 because Be atom has the smallest atomic radius among all the adatoms considered. Moreover, the adsorption-induced distortion of the plane of BC3 is very small for all the alkali and alkaline-earth metal atoms.

Table 1.

Properties of the metal atom adsorption on the BC3 sheet. FS represents the favorite sites of adatoms on the BC3, h is the adatom height defined as the difference between the adatom z coordinate and the average z coordinate of atoms in BC3, Δ is the adsorption-induced distortion deviating from the plane of BC3, ρad is the charge transfer from adatom to BC3, IP is the experimental ionization potential of the isolated atom, μiso and μtot are the magnetic moment of the isolated atom and the total magnetic moment of the system, p and Φ are the dipole moment and the work function, and Egap is the energy gap of the system. The “m” and “h” in Egap column represent metal and half-metal, respectively.

.

Figure 4(a) shows the DOS of B 2p, C 2p, and K 4s states of K adatoms at the H1 site of BC3. In comparison with the pristine BC3, the electronic states of BC3 remain almost unaltered except for the charge transfer from the adatom to the substrate. Thus the Fermi level EF is up-shifted, resulting in metal features of the K–BC3 structure. The 4s states of the K adatoms are empty and lie at 1.71 eV above EF. Thus there is about one electron charge (e) per adatom transferred from the alkali metal adatoms to the BC3 sheet. This effect has been tested by the Bader charge transfer from metal adatoms to BC3 listed in Table 1. For Li and Na adatoms on BC3, similar results are obtained. So the bonding of Li, Na, and K with BC3 is ionic. Meanwhile these structures have no magnetic moment. As a result, the effect of alkali metal adsorption on BC3 can be taken as the electron doping process only. In contrast, the Na and K adatoms on graphene are magnetic, with the spin-up s states of the adatoms lying close to EF.[19] For the pristine BC3 sheet there is a van Hove singularity at 1.71 eV above EF. Increasing the coverage capacity of alkali metal atoms on BC3, the van Hove singularity can be tuned to locate exactly at EF, which results in the formation of Fermi surface nesting.[37] In addition, the dependence of the dipole moments on adatom height h and the amount of charge transfer can be easily observed here. For example, the Ca–BC3 system exhibits the largest dipole moment of 6.64 debye in all cases investigated due to the relative high h (1.90 Å) and considerable charge transfer (1.30 e).

Fig. 4. (color online) PDOS for (a) K–BC3, (b) Ca–BC3, (c) Ga–BC3, and (d) Sn–BC3.

For the adsorption of Be, Mg, and Ca atoms on BC3, slight hybridization states occur close to EF as shown in Fig. 4(b). Figure 4(b) shows that the hybridizations between Ca 3d states and B 2p and C 2p states of BC3 appear around EF, which results in a partial covalent bond between Ca and the BC3 sheet. In the case of Mg adsorbing on BC3, the spin-up Mg 3p states hybridize with the substrate states around EF, contrasting with the spin-down Mg 3p states hybridizing with the substrate states far above EF. These electronic states result in the magnetism of the Mg–BC3 structure with a total magnetic moment of 0.95 μB. There are also large electron transfer from alkaline-earth metal adatoms to the BC3 sheet. For Be, Mg, and Ca the Bader electron transfers from adatoms to BC3 are 1.54 e, 0.89 e, and 1.30 e, respectively, revealing ionic and covalent mixed binding between the adatoms and the substrate.

3.1.2. Groups III and IV metal adatoms

The Eb of Al, Ga, and In on the BC3 sheet are almost three times as large as on graphene. Furthermore, the Eb of Sn adatom on BC3 is 2.75 eV with the ratio Eb/Ec of 0.88, which is an order of magnitude larger than that on graphene.[19] Due to the similar atomic radii of Al, Ga, In, and Sn, the adatom heights h of the four adatoms vary from 2.00 Å to 2.35 Å, and their dipole moments vary from 0.71 debye to 2.01 debye. The charge transfer from Al, Ga, In, and Sn adatoms to the substrate are 0.71 e, 0.51 e, 0.58 e, and 0.71 e, respectively, which are much less than the corresponding values of the valence electrons. There are remarkable hybridizations between the adatom p states and the substrate states around and below EF for Al, Ga, and In on BC3. Figure 4(c) shows the hybridizations between the Ga 4p states and the BC3 states around EF. For the adsorption of Sn adatom on BC3, similar hybridization features are observed, as shown in Fig. 4(d). Thus the bonding is mainly covalent for these adatoms on the BC3 sheet, instead of an ionic bonding between these adatoms and graphene.[19] In addition, for the Sn adatom on BC3, the Sn–BC3 structure seems to be a semiconductor with an energy gap (Eg) of 0.23 eV.

3.1.3. Transition and noble metal adatoms

For the adsorption of the transition and noble metal atoms on the BC3 sheet, the adatoms are strongly bounded to the H1 or H2 sites except for Au, which prefers to bond with the substrate at the B2 site. Among these transition metal adatoms, the Eb of Ti adatom is close to Ec, such that the ratio Eb/Ec is 0.93. The adatom d states are strongly hybridized with the B 2p and C 2p states of BC3 around EF for all these adatoms except Au, whose 6s states are hybridized with the substrate states near EF, as shown in Fig. 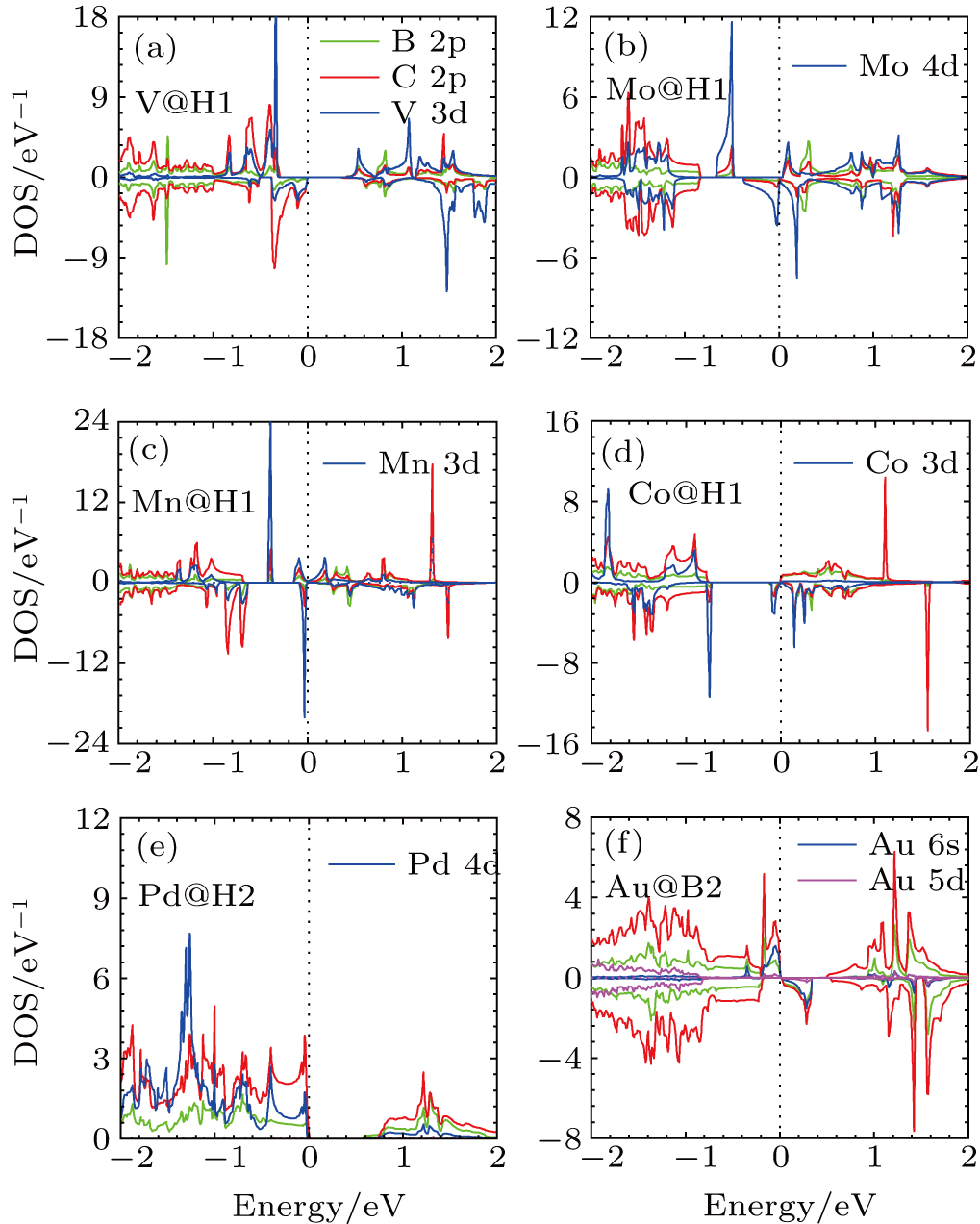5. Thus, the transition metal adatoms form strong covalent bonds with their nearest substrate atoms.

Fig. 5. (color online) PDOS for (a) V–BC3, (b) Mo–BC3, (c) Mn–BC3, (d) Co–BC3, (e) Pd–BC3, and (f) Au–BC3.

In details, figure 5(a) shows that for V–BC3 the occupation of the spin-up V 3d states is much larger than that of the spin-down V 3d states, which results in a total magnetic moment of 1.00 μB. For Cr, Mo, and W adatoms, in spite of the large Eb (3.46 eV) of W on BC3, the ratio Eb/Ec of them is less than 0.50. In addition, Mo adatom adsorption induces a distortion of 0.306 Å, which is the largest distortion in all the cases considered. Furthermore, the hybridizations between the adatoms d states and the BC3 states occur through almost the entire energy space, as shown in Fig. 5(b). For Mn, Fe, Co, and Ni, adatoms and substrate are relatively strongly bonded. Co adatom on the H1 site has the largest ratio Eb/Ec of 0.72. These adatoms prefer to adsorb on the H1 sites except Ni, which favors to reside at the H2 site. The adatom–BC3 structures are all magnetic. Figures 5(c) and 5(d) show that there are hybridizations between the adatoms and substrate around and below EF. For Pd, Pt, and Au, the electron transfers from the adatom to the substrate are smaller compared to their valence electrons. Thus, all the adatom–BC3 structures are semiconductors. Pd 4d (Pt 5d) states are hybridized with the B 2p and C 2p states of BC3 nearly throughout entire energy space, as shown in Fig. 5(e). For Au adatom, the Eb is 0.90 eV which is an order of magnitude larger than that on graphene,[19] and the magnetic moment of the Au–BC3 structure is 1.00 μB. Although the 5d shell of an isolated Au atom is fully filled, the Au 5d states are hybridized strongly with the substrate states below EF, in contrast to the hybridizations between the Au 6s states and substrate states occurring near EF, as shown in Fig. 5(f).

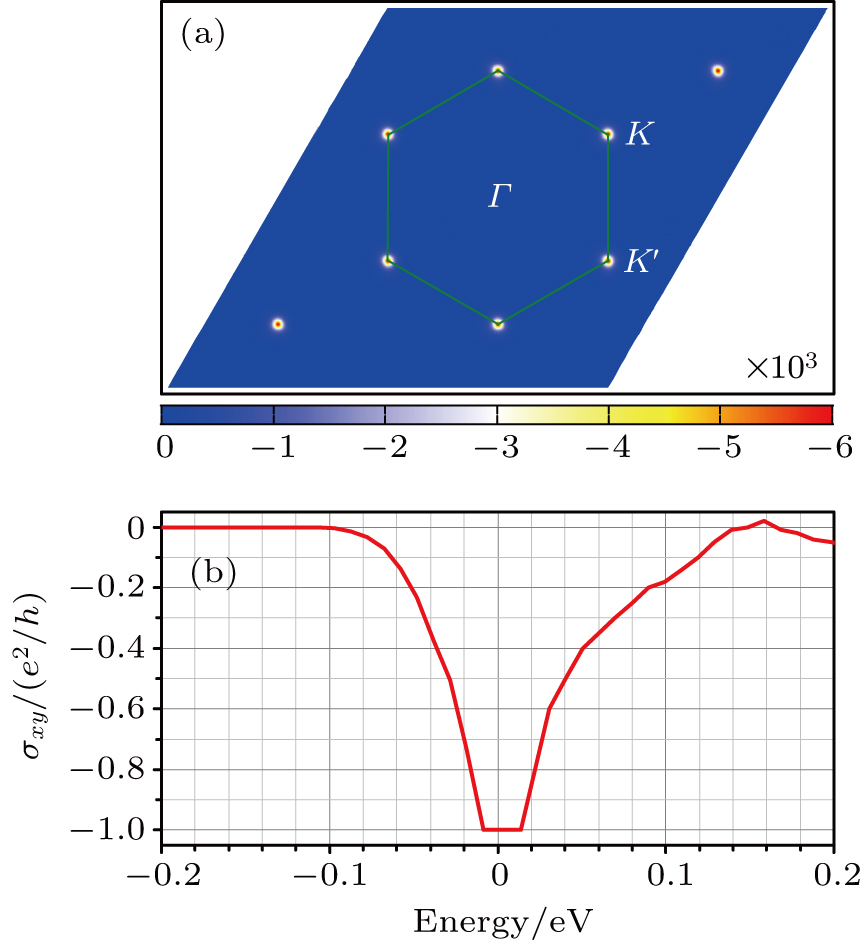
More interesting are the cases of Co, Mo, Mn, and Au adatoms on BC3. In Co–BC3 structure, there exists a single spin Dirac cone around EF, as shown in Figs. 6(a)–6(c). LDA calculation shows that the spin-down Dirac point exactly locates at EF with total magnetic moment of 1.00 μB. If the spin orbit coupling (SOC) interactions are taken into account, there is a 37 meV gap opening at the Dirac point, as shown in Fig. 6(c). This indicates that the metal atom adsorption increases the SOC interaction remarkably, and the Co–BC3 structure may be a quantum anomalous Hall (QAH) insulator,[52,53] which will be discussed later. For Mo and Mn adatom on BC3, the adatom–BC3 structures are half-metals with only single spin bands across EF, as shown in Figs. 6(d) and 6(e). For the adsorption of Au atom on the B2 site, the Au–BC3 system is a spin-semiconductor with a small intrinsic energy gap of 30 meV, and the bandwidths of the spin-up and spin-down states near EF are 0.18 eV and 0.30 eV, respectively, as shown in Fig. 6(f). These results imply great significance in spintronics.[54–56]

Fig. 6. (color online) Band structures for Co at the H1 site of the BC3 calculated with the (a) GGA, (b) LDA, and (c) LDA with SOC. (d), (e), and (f) show band structures for Mo–BC3, Mn–BC3, and Au–BC3, respectively.

For the Co–BC3 system, the ground state estimated from the LDA calculations is found to be ferromagnetic, which is about 211 meV and 45 meV lower than the nonmagnetic and antiferromagnetic states, respectively. To identify the topological property of the SOC induced insulating state, we also calculate the Berry curvature Ω(k) and Chern number for the Co–BC3 system.[57–59] The distribution of the Berry curvature Ω(k) (in atomic units a.u.) for the whole valence bands in the momentum space is shown in the top panel in Fig. 7, in which the nonzero Ω(k) is localized around the K and K′ points with the same sign. By integrating the Ω(k) over the first Brillouin zone, the anomalous Hall conductivity σxy as a function of the energy around the Fermi level is obtained, as shown in the bottom panel in Fig. 7. We can find that the quantized Hall conductance platform appears around the Fermi level and the width of the platform accords completely with the global band gap. The σxy of −e2/h means the Chern number of −1, which indicates that the Co–BC3 structure is topologically nontrivial and thus the two chiral edge channels will appear on each side of its sample, hinting the realization of the QAH effect. In addition, the magnetocrystalline anisotropy calculation shows that the energy of the out-of-plane spin orientation for the Co–BC3 system is about 0.2 meV lower than that of the in-plane spin orientation, implying that the Co–BC3 is a suitable system to observe the QAH state in experiment.

Fig. 7. (color online) (a) The distribution of the Berry curvature (in a.u.) for the whole valence bands in momentum space and (b) the anomalous Hall conductivity σxy around the Fermi level calculated from the LDA.
3.2. Relation of dipole moments vs. work functions

The dipole moment perpendicular to the substrate is determined by the real-space-charge rearrangement due to the interaction between the adatom and substrate. It is defined as[19]p = −∫ρ(z)zdz+ΣiZiezi, where ρ(z) is the electron density integrated over the xy-plane, i is the index of ion, Zi is the atomic number of ion, and zi is the z coordinate of ion. The work function, which denotes the energy to remove an electron from the adatom–substrate system, can be calculated as Φ = Evac−EF, where Evac is the reference vacuum energy which is determined from the electrostatic potential in the vacuum region. Thus the work function is sensitive to the charge transfer from adsorbate to substrate.

To reveal the correlations between the dipole moment p and the work function Φ, we have drawn the p–Φ plot in Fig. 8(a). Except for Pd and Pt adatoms on BC3, the work functions for all the adatom–BC3 structures are lower than the value for the bare BC3 sheet. The data for alkali or alkaline-earth metal atoms are linear, as shown by the gray line segments. The p–Φ trend for alkali metal adatoms on BC3 is consistent with the data of the adatom height h and the charge transfer, due to the dipole moments are sensitive to the adatom heights h and charge transfers. For Li, Na, and K, the adatom heights h vary from 1.67 Å to 2.50 Å, while the amount of electrons transferred from the adatoms to the substrate is nearly identical, resulting in the increased dipole moments and almost unaltered work functions. It can also be seen that the multivalent adatoms do not follow a particular trend. Figure 8(b) shows that Φ is correlated to the experimental ionization potential (IP) for an isolated atom.[51] IP represents the energy requiring to remove an electron from an isolated atom. The overall trend of IP–Φ plot is different from the plot drawn for adatoms on graphene.[19] Most of the points locate below the gray line. However, the IP–Φ plot for Li, Na, K, Ca, Ga, In, Sn, Ti, V, Cr, Ni, Pd, and Pt adatoms on BC3 is similar to that for adatom–graphene, which shows the trend that the adatom species with lower IP are more likely to transfer their outer-shell electrons to the substrate, thereby raising EF and lowering Φ. For other adatoms there is no such particular trend found.

Fig. 8. (color online) (a) The dipole moments p vs. the work functions Φ and (b) the IP vs. the work function Φ for all adatoms adsorbing on their most stable sites.
4. Conclusion

In summary, we have studied the adsorption properties of alkali, alkaline-earth, groups III–IV, and transition metals on the graphene-like BC3 sheet. Many interesting properties are concluded. (1) The interactions between the adatoms and the BC3 are quite strong in contrast to those found in adatoms-graphene. (2) For Li, Na, and K on BC3, the adatom s states lie far above from EF, which results in the ionic bond for these adatoms. For Be, Mg, and Ca adatoms, besides the ionic bonding, there exist hybridizations between adatoms and the substrate near EF. The Al, Ga, In, and Sn adatoms are covalently bounded with the nearest neighboring atoms of the BC3 sheet. The adatom d states of all transition metal atoms studied are strongly hybridized with the BC3 states around EF except for Au, whose s states are hybridized with the substrate near EF. (3) BC3 with Co adatom reveals a quantum anomalous Hall (QAH) insulator phase as inferred from LDA calculations. (4) For Mo and Mn adatoms on BC3, the structures exhibit half metal behavior, while the most stable Au–BC3 structure is spin-semiconductor. (5) For Li, Na, K, Ca, Ga, In, Sn, Ti, V, Cr, Ni, Pd, and Pt, there is a trend that adatom species with lower IP have lower Φ. These results indicate the potential applications of the functionalization of graphene-like BC3 with metal adatoms.

Reference
[1] Novoselov K S Geim A K Morozov S V Jiang D Zhang Y Dubonos S V Grigorieva I V Firsov A A 2004 Science 306 666
[2] Katsnelson M I Novoselov K S Geim A K 2006 Nat. Phys. 2 620
[3] Novoselov K S Geim A K Morozov S V Jiang D Katsnelson M I Grigorieva I V Dubonos S V Firsov A A 2005 Nature 438 197
[4] Berger C Song Z Li T Li X Ogbazghi A Y Feng R Dai Z Marchenkov A N Conrad E H First P N de Heer W A 2006 Science 312 1191
[5] Zhang Y Tan W Y Stormer H L Kim P 2005 Nature 438 201
[6] Elias D C Nair R R Mohiuddin T M G Morozov S V Blake P Halsall M P Ferrari A C Boukhvalov D W Katsnelson M I Geim A K Novoselov K S 2009 Science 323 610
[7] Sofo J O Chaudhari A S Barber G D 2007 Phys. Rev. 75 153401
[8] Sahin H Ataca C Ciraci S 2009 Appl. Phys. Lett. 95 222510
[9] Sahin H Ataca C Ciraci S 2010 Phys. Rev. 81 205417
[10] Topsakal M Cahangirov S Ciraci S 2010 Appl. Phys. Lett. 96 091912
[11] Dikin D A Stankovich S Zimney E J Piner R D Dommett G H B Evmenenko G Nguyen S T Ruoff R S 2007 Nature 448 457
[12] Eda G Fanchini G Chhowalla M 2008 Nat. Nanotechnol. 3 270
[13] Robinson J T Perkins F K Snow E S Wei Z Sheehan P E 2008 Nano Lett. 8 3137
[14] Nair R R Ren W Jalil R Riaz I Kravets V G Britnell L Blake P Schedin F Mayorov A S Yuan S Katsnelson MI Cheng H M Strupinski W Bulusheva L G Okotrub A V Grigorieva I V Grigorenko A N Novoselov K S Geim A K 2010 Small 6 2877
[15] Robinson J T Burgess J S Junkermeier C E Badescu S C Reinecke T L Perkins F K Zalalutdniov M K Baldwin J W Culbertson J C Sheehan P E Snow E S 2010 Nano Lett. 10 3001
[16] Withers F Dubois M Savchenko A K 2010 Phys. Rev. 82 073403
[17] Leenaerts O Peelaers H Hernandez-Nieves A D Partoens B Peeters F M 2010 Phys. Rev. 82 195436
[18] Sahin H Topsakal M Ciraci S 2011 Phys. Rev. 83 115432
[19] Chan K T Neaton J B Cohen M L 2008 Phys. Rev. 77 235430
[20] Ataca C Aktürk E Ciraci S Ustunel H 2008 Appl. Phys. Lett. 93 043123
[21] Ataca C Aktürk E Ciraci S 2009 Phys. Rev. 79 041406(R)
[22] Ao Z M Peeters F M 2010 Phys. Rev. 81 205406
[23] Profeta G Calandra M Mauri F 2012 Nat. Phys. 8 131
[24] Zhang H Lazo C Blügel S Heinze S Mokrousov Y 2012 Phys. Rev. Lett. 108 056802
[25] Cao C Wu M Jiang J Cheng H P 2010 Phys. Rev. 81 205424
[26] üAktu\"rk O Tomak M 2009 Phys. Rev. 80 085417
[27] Krasheninnikov A V Lehtinen P O Foster A S Pyykkö P Nieminen R M 2009 Phys. Rev. Lett. 102 126807
[28] Rodríguez-Manzo J A Cretu O Banhart F 2010 ACS Nano 4 3422
[29] Beheshti E Nojeh A Servati P 2011 Carbon 49 1561
[30] Liu C Zeng Z 2010 Appl. Phys. Lett. 96 123101
[31] Kim G Jhi S Lim S Park N 2009 Phys. Rev. 79 155437
[32] Liu J Wu J Chen C Han L Zhu Z Wu J 2017 Int. J. Mod. Phys. 32 1850033
[33] Yanagisawa H Tanaka T Ishida Y Matsue M Rokuta E Otani S Oshima C 2004 Phys. Rev. Lett. 93 177003
[34] Tanaka H Kawamata Y Simizu H Fujita T Yanagisawa H Otani S Oshima C 2005 Solid State Commun. 136 22
[35] Yang Z Ni J 2012 Appl. Phys. Lett. 100 183109
[36] Zhao Y Dai Z Sui P Wang W 2014 J. Phys. Chem. Solids 75 1137
[37] Chen X Ni J 2013 Phys. Rev. 88 115430
[38] Chen X Yao Y Yao H Yang F Ni J 2015 Phys. Rev. 92 174503
[39] Lin X Ni J 2012 Phys. Rev. 86 075440
[40] Sahin H Peeters F M 2013 Phys. Rev. 87 085423
[41] Kresse G Hafner J 1993 Phys. Rev. 47 558
[42] Kresse G Joubert D 1999 Phys. Rev. 59 1758
[43] Perdew J P Burke K Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
[44] Monkhorst H J Pack J D 1976 Phys. Rev. 13 5188
[45] Makov G Payne M C 1995 Phys. Rev. 51 4014
[46] Neugebauer J Scheffler M 1992 Phys. Rev. 46 16067
[47] Miyamoto Y Rubio A Louie S G Cohen M L 1994 Phys. Rev. 50 18360
[48] Yanagisawa H Tanaka T Ishida Y Matsue M Rokuta E Otani S Oshima C 2004 Phys. Rev. Lett. 93 177003
[49] Mills G Jónsson H Schenter G K 1995 Surf. Sci. 324 305
[50] Kittel C 2005 Introduction to Solid Sate Physics 8 New York Wiley
[51] Martin W C Wiese W L 1996 Atomic, Molecular, and Optical Physics Handbook Drake G W F New York American Institute of Physics 135 153
[52] Yu R Zhang W Zhang H J Zhang S C Dai X Fang Z 2010 Science 329 61
[53] Jin H Im J Freeman A J 2011 Phys. Rev. 84 134408
[54] Son Y Cohen M L Louie S G 2006 Nature 444 347
[55] Wang X L 2008 Phys. Rev. Lett. 100 156404
[56] Zhao Y Ni J 2014 Phys. Chem. Chem. Phys. 16 15477
[57] Weng H M Dai X Fang Z 2014 Progress in Physics 34 1
[58] Ding J Qiao Z Feng W Yao Y Niu Q 2011 Phys. Rev. 84 195444
[59] Zhang H Lazo C Blügel S Heinze S Mokrousov Y 2012 Phys. Rev. Lett. 108 056802