† Corresponding author. E-mail:
The current study investigates the influence of temperature on a one-dimensional piezoelectric phononic crystal using tunable resonant frequencies. Analytical and numerical examples are introduced to emphasize the influence of temperature on the piezoelectric phononic crystals. It was observed that the transmission spectrum of a one-dimensional phononic crystal containing a piezoelectric material (0.7 PMN-0.3PT) can be changed drastically by an increase in temperature. The resonant peak can be shifted toward high or low frequencies by an increase or decrease in temperature, respectively. Therefore, we deduced that temperature can exhibit a large tuning in the phononic band gaps and in the local resonant frequencies depending on the presence of a piezoelectric material. Such result can enhance the harvesting energy from piezoelectric materials, especially those that are confined in a phononic crystal.
Over the past two decades, the propagation of acoustic/elastic waves using smart composite materials called phononic crystals (PnC) has received significant attention. The most important feature of PnC is the phononic band gap (PBG), which results from Bragg scattering or local resonance phenomena.[1–7] For Bragg scattering, the PBG is created at the boundary of the Brillion zone and its frequency is approximately equal to the lattice constant.[8–10] Liu et al. introduced the local resonance phenomena in a three-dimensional PnC, and the frequency of the PBG is two orders of magnitude smaller than its counterpart in Bragg scattering.[10] Owing to the presence of the PBG, PnCs have many significant applications, such as in acoustic filters, sensors, and waveguides.[11–15]
The resonance in PnCs is a very important phenomenon. The resonant mode (RM) can be generated inside the PBG by the introduction of defects in a regular PnC and it is defined as the maximum transmission peak inside the PBG.[16,17] These RMs are used widely in sensing applications owing to the link between the resonance frequency and the acoustic properties of the constituent materials.[18] RM can be altered and controlled using many parameters. Zubtsov et al. altered the position of the defect modes in PBGs by changing the concentration of the defect material.[16,18] In addition, Wang et al. could control the position of the RM by controlling the applied voltage based on the piezoelectric defect layer.[19]
Recently, new trends in PnCs have been studied and applied in society. Piezoelectric PnC is an important trend in the field of PnCs. Piezoelectric PnC is a PnC whose composite material contains a piezoelectric material. By using the plane wave expansion method, the 1-3 type piezoelectric composite has been studied by Wilm et al.[20] Li et al. analyzed the localization of the waves using disordered periodic layered piezoelectric composites.[21–23] Pang et al. studied the band structure of piezoelectric/piezomagnetic PnCs.[24] Aly et al. studied the effect of an external electric field on the position of the RM inside the band gap of a piezoelectric PnC.[25] The effects of initial stresses on the dispersion relations of elastic waves in a one-dimensional (1D) piezoelectric phononic crystal were studied by Guo and Wei.[26] The anisotropic nature of piezoelectric materials and the mechanic–electronic coupling nature are the most evident differences between the piezoelectric and isotropic materials.
In this paper, we present a 1D piezoelectric PnC analyzed using the transfer matrix method. In addition, we will introduce the influence of the relationship between the temperature and piezoelectric coefficient on the RM position inside the band gap. It is concluded that our structure can be used as a temperature sensor.
The 1D PnC structure, which is composed of periodically alternating layers of aluminum and epoxy with thicknesses of a1 and a2, respectively, is presented in Fig.
 |
 | Fig. 1. (color online) (a) PnC structure composed of a periodic structure of Al and epoxy layers and (b) defected PnC structure with 0.7 PMN-0.30PT as a defect layer. |
The solution of Eq. (
 |
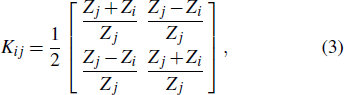 |
 |
 |
 |
In this section, we consider the propagation of normal incident acoustic waves in a 1D PnC composed of four unit cells with each unit cell composed of Al/epoxy. We assume that the entire structure is bounded by water as a semi-infinite material. The presence of water does not support the shear waves through the structure. The thicknesses of the first and second layers are 
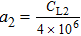
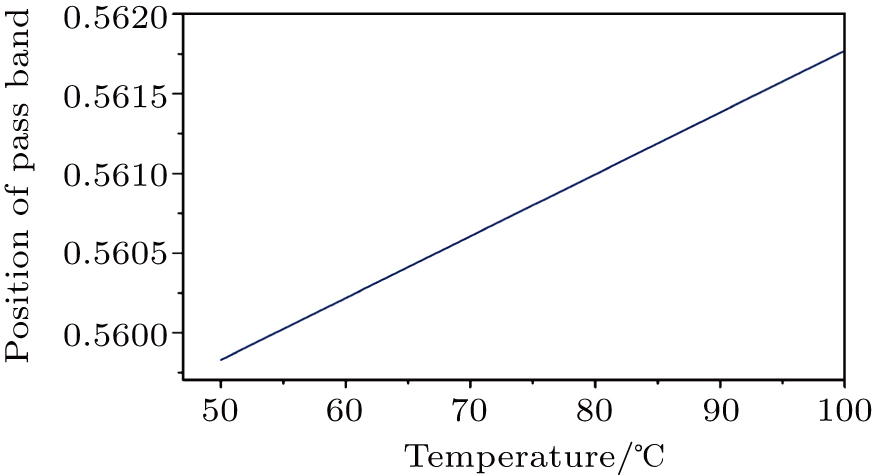
Figure
 | Fig. 2. Relationship between temperature and piezoelectric constant d33.[16] |
From Fig. 
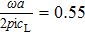

 | Fig. 3. (color online) Transmission spectra for (a) PnC composed of a periodic structure of Al and epoxy layers. (b) Defected PnC with 0.7 PMN-0.3PT with the thickness of CL3/2 × 106 m. |
We can observe from Fig.
Figure
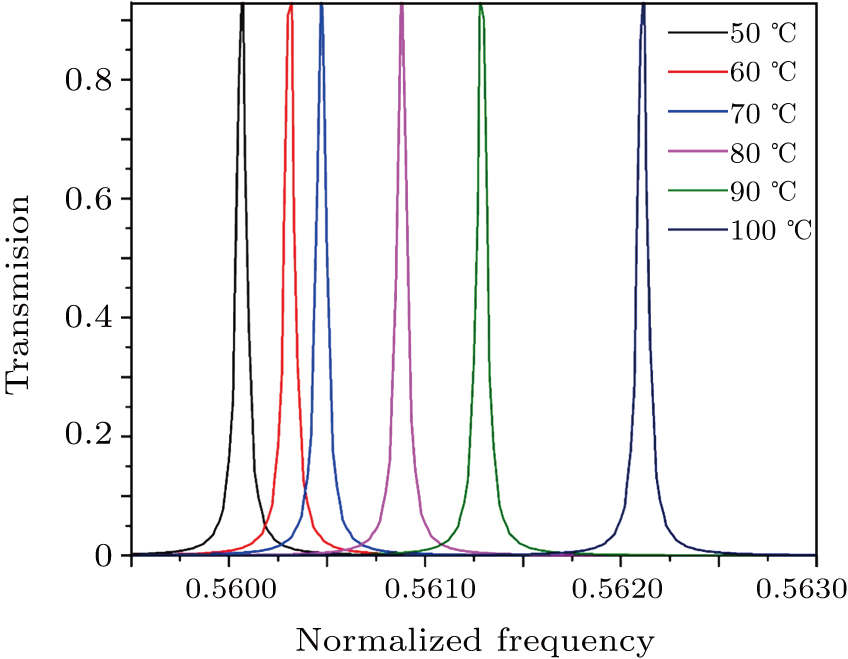 | Fig. 4. (color online) Transmission spectra of defected PnC with 0.7 PMN-0.3PT at different temperatures. |
In this study, we investigated the effects of temperature on the transmission properties of a 1D piezoelectric PnC structure. The results revealed that inserting a piezoelectric material (0.7 PMN-0.3PT) inside a perfect PnC could produce a sharp resonant peak inside the transmission spectrum of the PnC. Such a peak is significantly shifted toward higher frequencies with an increase in temperature. Moreover, it can be shifted toward lower frequencies with a decrease in temperature. Therefore, tuning the band gaps in PnCs can be easily achieved by changing the temperature. In summary, to the best of our knowledge, this is the first time that PBGs were tuned by controlling the temperature.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |