Project supported by the Natural Science Foundation of Zhejiang Province, China (Grant No. LY15F050010) and the National Natural Science Foundation of China (Grant Nos. 11604296, 11404286, and 61727821).
Project supported by the Natural Science Foundation of Zhejiang Province, China (Grant No. LY15F050010) and the National Natural Science Foundation of China (Grant Nos. 11604296, 11404286, and 61727821).
† Corresponding author. E-mail:
Project supported by the Natural Science Foundation of Zhejiang Province, China (Grant No. LY15F050010) and the National Natural Science Foundation of China (Grant Nos. 11604296, 11404286, and 61727821).
By using the designed photonic crystal fiber filled with argon gas, the effect of gas pressure on modulation instability (MI) gain is analyzed in detail. The MI gain bandwidth increases gradually as the argon gas pressure rises from 1P0 to 400P0 (P0 is one standard atmosphere), while its gain amplitude slightly decreases. Moreover, the increase of the incident light power also results in the increase of MI gain bandwidth in the Stokes or anti-Stokes region when the incident power increases from 1 W to 200 W. Making use of the optimal parameters including the higher argon gas pressure (400P0) and the incident light power (200 W), we finally obtain a 100 nm broadband MI gain. These results indicate that controlling the MI gain characteristic by changing the argon gas pressure in PCF is an effective way when the incident light source is not easy to satisfy the requirement of practical application. This method of controlling MI gain can be used in optical communication and laser shaping.
Modulation instability (MI) process has been observed and studied in some fields, such as fluid dynamics, nonlinear optics, and plasma physics.[1–3] The physical mechanism of MI is the interplay between the nonlinear and dispersive effects. Although MI may bring some negative effects into some systems such as optical communication, it can also be useful. In the optical field, MI plays an essential role in four-wave mixing (FWM) process, wavelength conversion, and optical amplification. And it has been used to produce optical pulse trains[4] and optical solitons,[5] make MI laser,[6] and supercontinuum (SC) generation.[7] For the fiber, our previous research results show that the MI gain mainly depends on the fiber dispersion, the fiber nonlinearity, and stimulate Raman scattering.[8–10] Among them, the Raman scattering effect is mainly determined by the fiber substrate material (for example, fused silica), which is not easy to change once fiber is made. Thus, in order to manipulate the MI gain in experiment effectively, it is convenient to adjust the fiber structure or its refractive index distribution for controlling the fiber dispersion and nonlinearity.
Compared with the ordinary step-index fiber, the photonic crystal fiber, as a microstructure fiber, has an advantage of the flexible structural design,[11,12] which makes it easy and effective to obtain a tunable MI gain. Considering the photonic crystal fiber (PCF) dispersion and nonlinearity depending on the fiber structure, a tunable MI gain is usually obtained by changing the geometry structure of PCF or choosing the different incident light based on the fiber zero dispersion wavelength (ZDW). Although these methods are feasible theoretically, they not only waste more time but also increase the experimental cost. One reason is that some commercial light sources satisfying the experimental requirement are not easy to find in practice, especially for a light source with a high power and a tunable wavelength. The other reason is that the ZDW of PCF is invariable once it is made, which cannot be used to obtain a tunable MI gain. In this work, based on the existing commercial light source with a high output power, we will firstly fill the argon gas into the PCF, and study the pressure-dependent tunable MI gain characteristic by varying the pressure of argon gas in the PCF, which can control the PCF dispersion and nonlinearity conveniently.
For a non-birefringence photonic crystal fiber, the MI gain expression can be obtained by adding small perturbations into the steady solution of the scalar nonlinear SchrÖdinger equation (NLSE), which includes the nonlinear effects such as fiber dispersion, self-phase modulation (SPM), self-steepening (SS), stimulated Raman scattering (SRS), and four-wave mixing (FWM). It is written as[13]
 |
 |
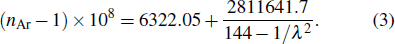 |
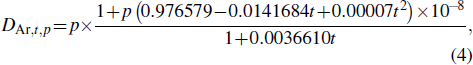 |
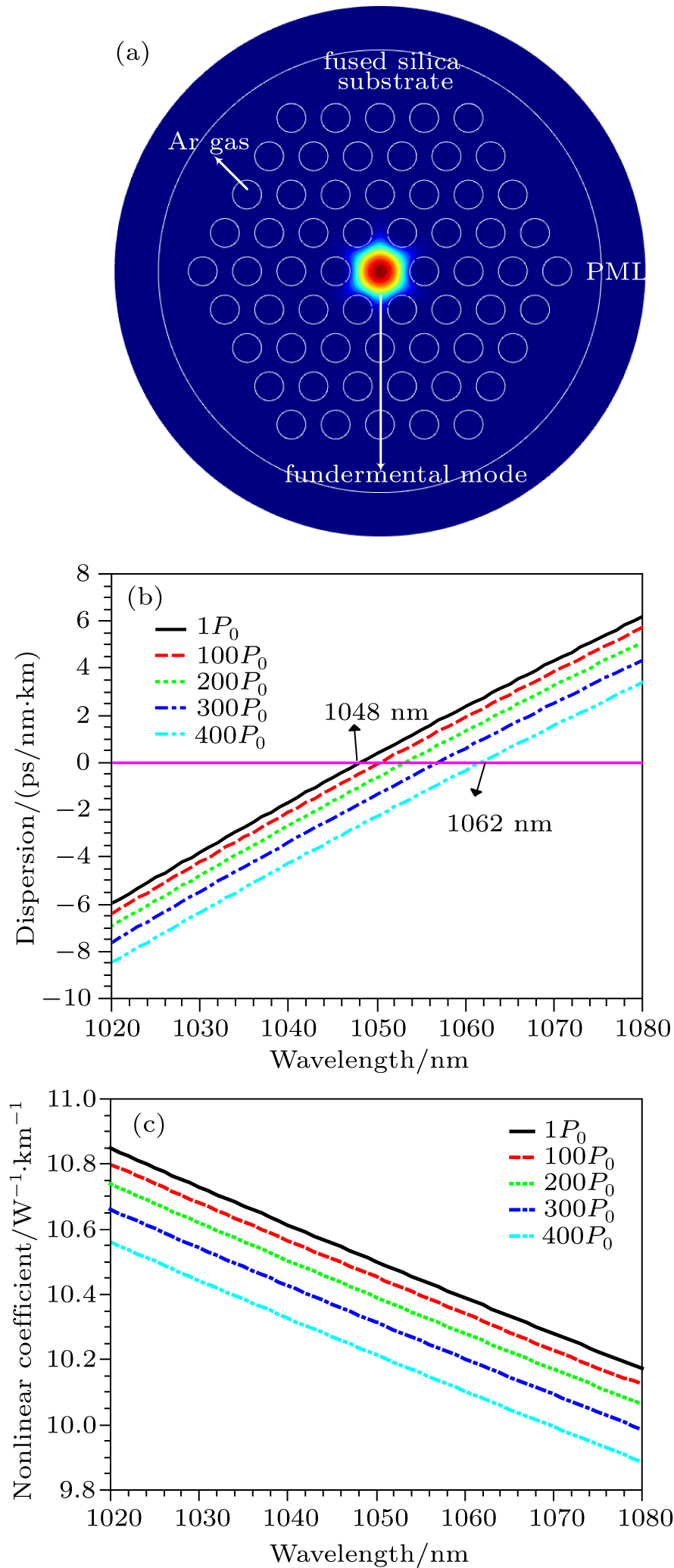
For studying the effect of argon gas on MI gain, a fused silica PCF filled with argon gas is designed with finite-difference frequency-domain techniques. Figure
Figure
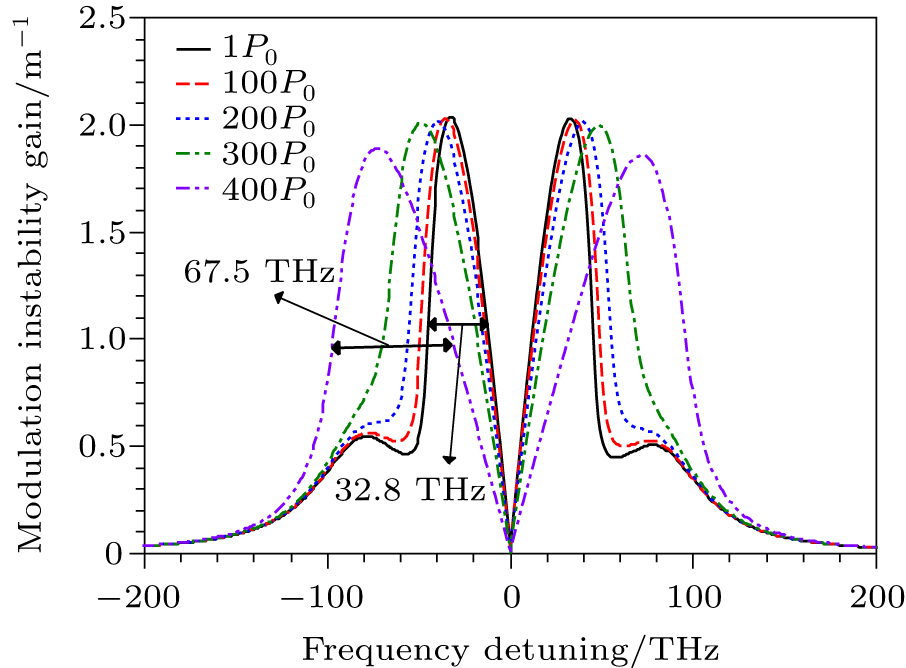 | Fig. 2. (color online) MI gain variations with frequency detuning for different gas pressures with pump power fixed at 100 W. |
In the above section, we mainly discussed the effect of gas pressure on the MI gain bandwidth and amplitude at pump power Pp = 100 W. The following part will analyze the influences of the incident power on the MI gain at different gas pressures. Figure
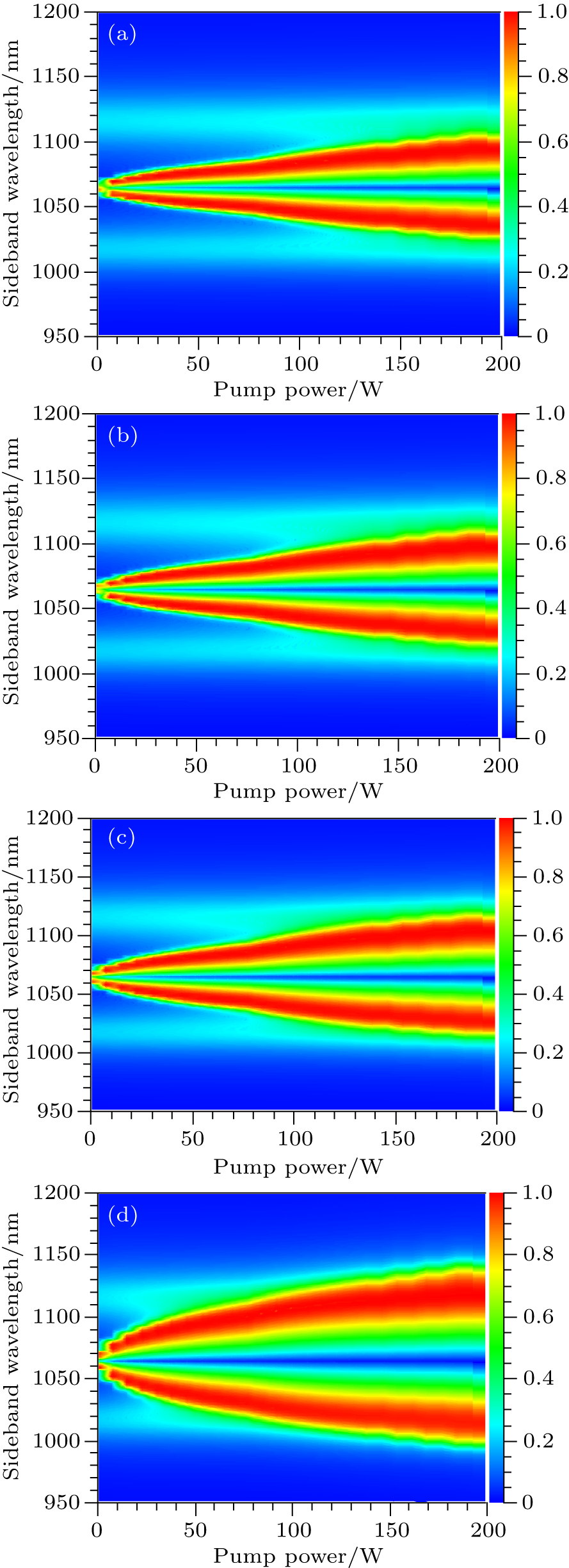 | Fig. 3. (color online) Variations of MI sideband wavelength with incident power at different gas pressures: (a) 100P0, (b) 200P0, (c) 300P0, (d) 400P0. |
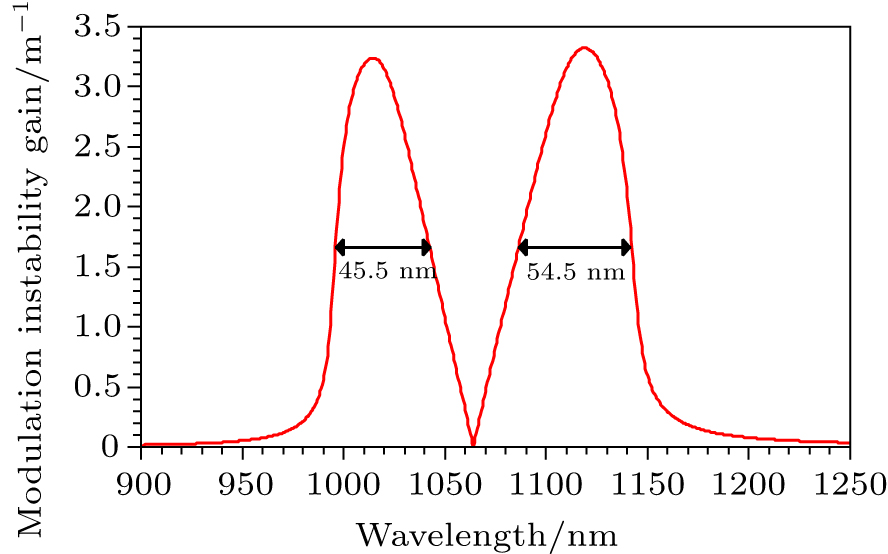
The former analysis reveals that the optimal incident power and the argon gas pressure may be set to be 200 W and 400P0 respectively for obtaining a broadband MI gain. Using the two optimal parameters, the optimal MI gain spectrum is obtained finally and shown in Fig.
Based on the designed PCF fiber filled with argon gas, pressure- and power-dependent MI gain is studied. The results show that it is effective to control the MI gain bandwidth and amplitude by changing the incident power and the argon gas pressure in the PCF fiber. When the gas pressure increases from 1P0 to 400P0, the MI gain bandwidth increases gradually while its gain amplitude decreases slightly. Besides, the incident light power also has an important effect on the MI gain. The MI gain peak in the Stokes or anti-Stokes region strays from the incident wavelength (1064 nm) gradually when the incident power increases from 1 W to 200 W, and their gain bandwidths also gradually widen. These results indicate that it is a feasible way to gain a tunable MI gain by changing the argon gas pressure when the incident light source is difficult to satisfy the requirement, and the PCF fiber with an appropriate ZDW cannot be made. And it may be useful in the fiber laser, fiber communication, and fiber sensor in the future.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] |