Project supported by the Fundamental Research Funds for the National Defense Basic Scientific Research, China (Grant No. JCKY2016603C007).
Project supported by the Fundamental Research Funds for the National Defense Basic Scientific Research, China (Grant No. JCKY2016603C007).
† Corresponding author. E-mail:
Project supported by the Fundamental Research Funds for the National Defense Basic Scientific Research, China (Grant No. JCKY2016603C007).
Geiger mode avalanche photodiode detector (Gm-APD) possesses the ultra-high sensitivity. Photon counting chirped amplitude modulation (PCCAM) light detection and ranging (lidar) uses the counting results of the returned signal detected by Gm-APD to mix with the reference signal, which makes PCCAM lidar capable of realizing the ultra-high sensitivity, and this is very important for detecting the remote and weak signal. However, Gm-APD is a nonlinear device, different from traditional linear detectors. Due to the nonlinear response of Gm-APD, the counting results of the returned signal detected by Gm-APD are different from those of both the original modulation signal and the reference signal. This will affect the mixing effect and thus degrade the detection performance of PCCAM lidar. In this paper, we propose a response probability correction method. First, the response probability correction model is established on the basis of Gm-APD Poisson probability response model. Then, the response probability correction model is used to adjust the original modulation signal that is used to drive laser, in order to make the counting results of the returned signal detected by Gm-APD better mix with the local reference signal in the same form. Through this method, the detection performance of PCCAM lidar is enhanced efficiently.
In the past several decades, light detection and ranging (lidar) has been widely used in various fields, and it possesses the advantages of good directionality, high spatial resolution, and detection accuracy.[1–3] Now, many application backgrounds of remote and weak signal detection put forward higher requirements for the detection sensitivity. In this case, the scattered photons are very rare (called photon starved scenes), normally a few photons or less than a single photon. Therefore, conventional approaches are quite invalid due to the limitation of the detector sensitivity.[4,5] Geiger mode avalanche photodiode detector (Gm-APD) is a new kind of detector working in critical state with a bias voltage slightly higher than the breakdown voltage, and thus Gm-APD has an ultra-high sensitivity, even responding to a single photon.[6–9] Shortly after the Gm-APD detector appeared, MIT Lincoln Laboratory conducted the first experiment with a single detector, which showed the feasibility of using a Gm-APD for 3D imaging.[10,11] East China Normal University demonstrated various methods of laser ranging using Gm-APD single-photon detectors, including laser ranging with 1-GHz sine-wave gated InGaAs/InP APD single-photon detector,[12] single-photon ranging system with multiple repetition rates for reducing the range ambiguity,[13] coincidence photon-counting laser ranging for moving targets with high signal-to-noise ratio,[14] etc. Subsequently, many groups conducted a substantial amount of research work on the performance of Gm-APD lidar, which showed that Gm-APD detection technology is an effective way to detect the weak signal.[15,16] Besides, the heterodyne detection is also an effective way to detect the weak signal, and it could improve receiver sensitivity compared with direct detection due to the mixing process of echo signal and reference signal.[17,18] Therefore, a bold and innovative idea was proposed: whether a combination of the Gm-APD single photon detection and the heterodyne detection is feasible. The answer is yes, and this is completely feasible. In 2006, the Army Research Laboratory used Gm-APD in the chirped amplitude modulation (CAM) lidar for the first time, and proposed photon counting chirped amplitude modulation (PCCAM) lidar.[19] In 2015, East China Normal University demonstrated photon-counting chirped amplitude modulation lidar with 1.5-GHz gated InGaAs/InP Gm-APD.[20]
This novel PCCAM lidar could yield high sensitivity approaching the signal shot noise limit, and thus became a hot research topic. In this respect, we have made significant research efforts. In 2011, the sliding window and the threshold were used to reduce the error photon counting pulses that were caused by noise and mostly distributed in the intensity troughs of the chirped AM waveform, and this method efficiently improved the signal noise ratio (SNR) of PCCAM lidar.[21] In 2013, a new premixing method for PCCAM lidar was proposed, and it adopted the reference signal to directly modulate the sampling gate width of the Gm-APD to complete the mixing process before Gm-APD. This new premixing method could improve the SNR due to avoiding the noise introduction from a separated mixer commonly used in the traditional PCCAM lidar.[22] In the same year, an echo signal intensity optimization strategy with an iris diaphragm was employed in PCCAM lidar, and the experimental results demonstrated that it could effectively improve the SNR of PCCAM lidar under different signal and noise intensities.[23] Through a lot of research efforts, we also found that due to the nonlinear Poisson response of Gm-APD, the photon counting results of the returned CAM signal are a joint function of the CAM signal and Poisson probability response. The photon counting results have different functional forms with the original modulation signal and the reference signal, which would affect the mixing effect and thus degrade the detection performance of PCCAM lidar. Therefore, in this paper, we present an improved method of PCCAM lidar based on the response probability correction. Through the response probability correction, we are able to ensure that the photon counting results of the returned CAM signal and the local reference signal are in the same form, which will lead to a better mixing effect and improve the detection performance of PCCAM lidar.
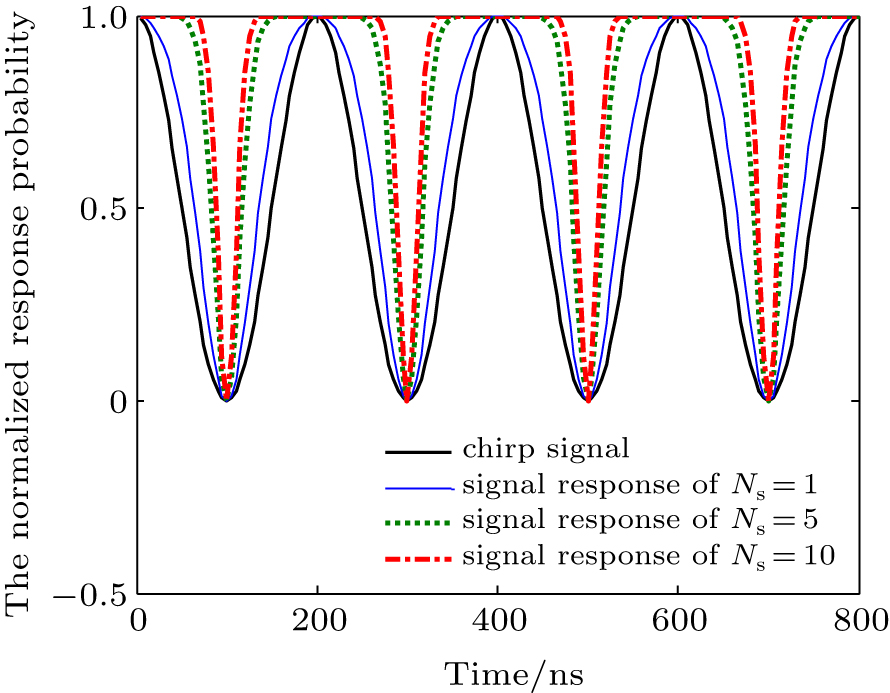
PCCAM lidar originates from the traditional chirped amplitude modulation lidar. They both use chirped amplitude modulation (CAM) signal, whose normalized form can be expressed as
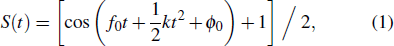 |
However, Gm-APD is different from the traditional linear response detector, it is a nonlinear device. The probability response model of Gm-APD meets the Poisson probability distribution and can be expressed as[24]
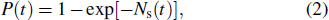 |
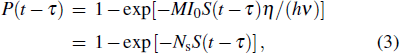 |
In Fig.
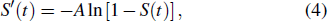 |
The operational principle of the improved PCCAM lidar using response probability correction is shown in Fig.
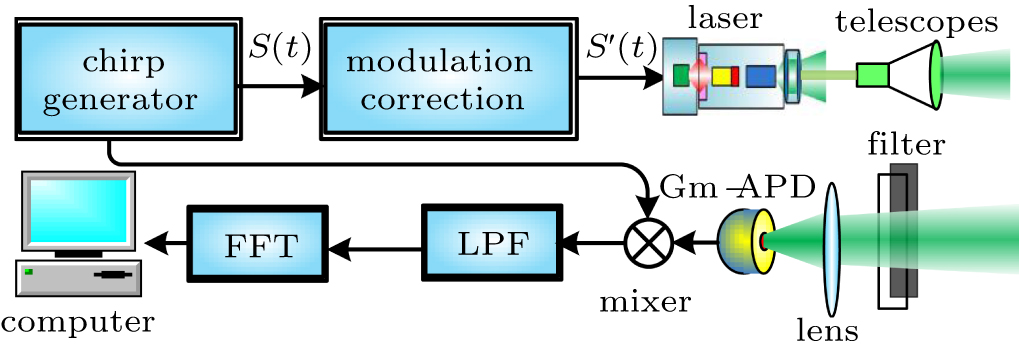 | Fig. 2. (color online) Schematic diagram of the improved PCCAM lidar system with response probability correction. LPF stands for low-pass filter; FFT denotes fast Fourier transform. |
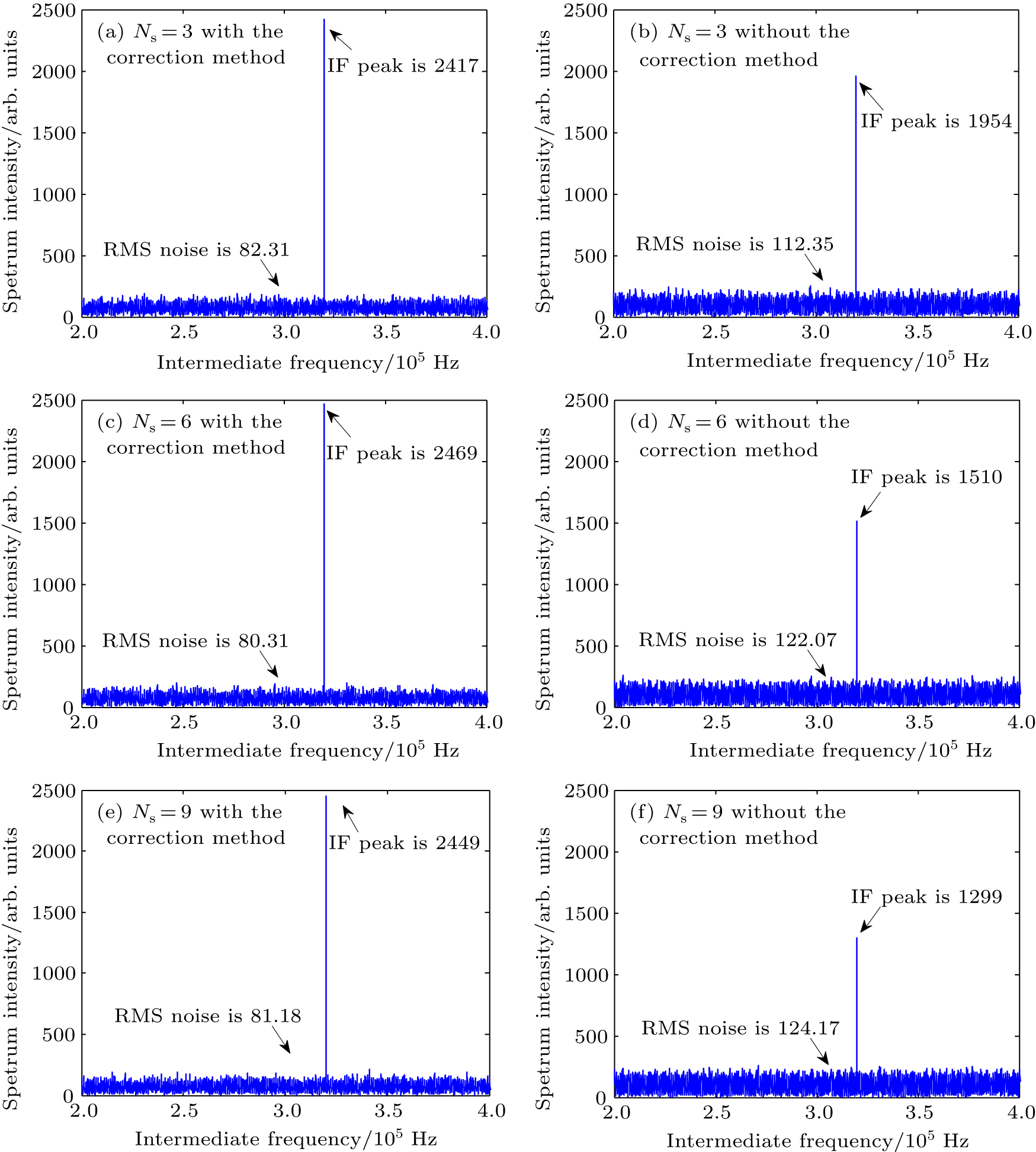
Under the same conditions, we compare two methods: one is the improved PCCAM lidar system that is proposed in this paper with response probability correction method; the other is the traditional PCCAM lidar system without response probability correction method. From Fig.
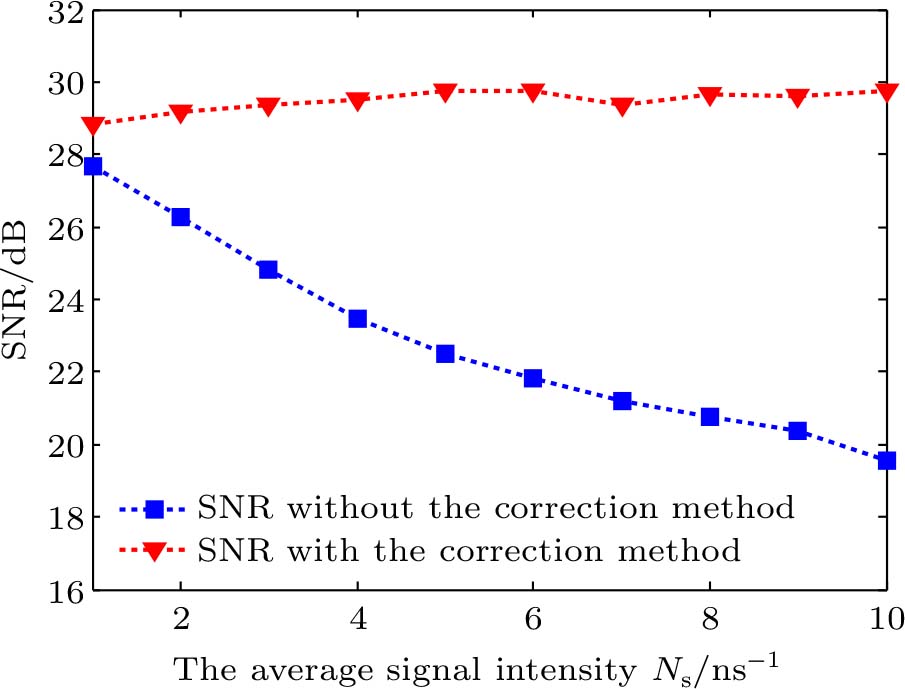 | Fig. 4. (color online) Comparison between signal noise ratio (SNR) with and without the correction method. |
The SNR is the ratio of the IF signal to the RMS noise in dB. Many performance parameters of the PCCAM lidar system will be improved with the increase of SNR, such as the range accuracy 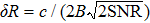
We present an improved PCCAM lidar system based on the response probability correction method. First, the response probability correction model is deduced through the theoretical analysis. Then the response probability correction model is used to adjust the laser signal. This method makes the photon counting results of the echo CAM signal and the local reference signal be in the same form, thus ensuring the better mixing effect. Finally the experimental results show that the proposed correction method in this paper is capable of obtaining better IF signal and lower RMS noise, and thus efficiently improving the SNR of PCCAM lidar system.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] |