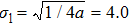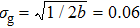Project supported by the National Natural Science Foundation of China (Grant Nos. 61771067, 61631014, 61471051, and 61401036) and the Youth Research and Innovation Program of Beijing University of Posts and Telecommunications, China (Grant Nos. 2015RC12 and 2017RC10).
Project supported by the National Natural Science Foundation of China (Grant Nos. 61771067, 61631014, 61471051, and 61401036) and the Youth Research and Innovation Program of Beijing University of Posts and Telecommunications, China (Grant Nos. 2015RC12 and 2017RC10).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61771067, 61631014, 61471051, and 61401036) and the Youth Research and Innovation Program of Beijing University of Posts and Telecommunications, China (Grant Nos. 2015RC12 and 2017RC10).
The coherent-mode representation theory is firstly used to analyze lensless two-color ghost imaging. A quite complicated expression about the point-spread function (PSF) needs to be given to analyze which wavelength has a stronger affect on imaging quality when the usual integral representation theory is used to ghost imaging. Unlike this theory, the coherent-mode representation theory shows that imaging quality depends crucially on the distribution of the decomposition coefficients of the object imaged in a two-color ghost imaging. The analytical expression of the decomposition coefficients of the object is unconcerned with the wavelength of the light used in the reference arm, but has relevance with the wavelength in the object arm. In other words, imaging quality of two-color ghost imaging depends primarily on the wavelength of the light illuminating the object. Our simulation results also demonstrate this conclusion.
Ghost imaging is an indirect and nonlocal imaging method. The new imaging technique permits to image an object with single-pixel detector, which is realized by correlating the signals from two optical paths, the object arm and the reference arm. The object light which illuminates the object imaged is detected by a detector without any spatial resolution ability (a single-pixel detector or a bucket detector), and the reference light which does not usually interact with the object is detected by a spatial resolvable detector. The object information can be reconstructed by registering the intensity correlation as a function of the transverse position of the reference detector.
The realization of the imaging technique was attributed to quantum correlations associated with entangled photons generated by parametric down-conversion,[1–3] and the classically correlated light which is generated by illuminating a laser beam through a rotating ground class.[4–7] Recently, there have been many researches on new imaging schemes and methods. Ghost imaging technique combined with computer generated random patterns (computational ghost imaging),[8,9] sparsity constraints,[10,11] and compressive sensing[12,13] were investigated. Imaging through different circumstances, including turbulent atmosphere,[14–16] scattering media,[17–19] turbid media,[20] and refractive media,[21] were studied. Ghost imaging with the reflective targets were analyzed theoretically and experimentally.[22–24] The scheme of ghost imaging lidar which can be used in the field of remote sensing was also proposed.[10,25–28]
Note that the most work focused on ghost imaging with monochromatic thermal light. Recently, some works have discussed two-color, even multi-wavelength ghost imaging.[29–32] Chan et al. firstly studied two-color ghost imaging using either thermal or quantum light sources. Their results showed that the resolution of two-color thermal ghost imaging can be higher than its quantum counterpart. By a very complicated point-spread function (PSF), they also showed that the spatial resolution of ghost-image depends primarily on the wavelength used to illuminate the object.[29] A new coherent-mode representation theory was reported to analyze ghost imaging with classical light source, and the results showed that this theory is suitable for evaluating imaging quality in 2f, f−2f, and lensless Fourier-transform ghost imaging systems.[33] We discussed the possibility that the theory is used in a ghost microscope imaging system.[34] However, whether the coherent-mode representation can be used to analyze lensless two-color ghost imaging is not mentioned in these works.
In this paper, we investigate lensless two-color ghost imaging by using the coherent-mode representation theory. It is shown that the intensity fluctuation correlation function in a lensless two-color ghost imaging system can be changed from the usual two-dimensional integral representation to a new one-dimensional summation representation, based on which imaging quality can be analyzed by the distribution variety of the decomposition coefficients of the object imaged. By the analytical and numerical results, we show that the decomposition coefficients are only related to the wavelength used in the object arm. The theory is quite suitable for evaluating which wavelength has a stronger effect on imaging quality in two-color ghost imaging.
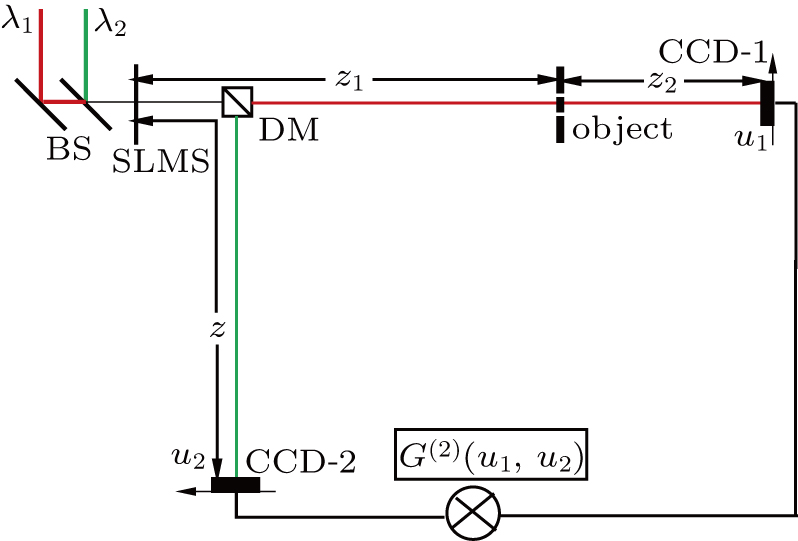
To demonstrate two-color ghost imaging, a conventional lensless ghost imaging system with pseudothermal light needs minor modification, as shown in Fig.
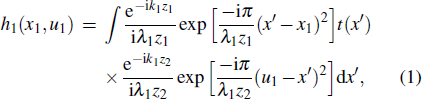 |
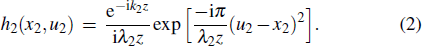 |
The information of the object can be retrieved by measuring intensity fluctuation correlation function[6]
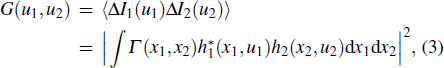 |
Based on the second-order coherence theory of optical fields, Γ(x1, x2) can be expressed in the coherent-mode representation[35] as
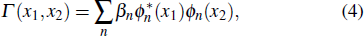 |
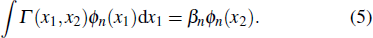 |
Substituting Eq. (
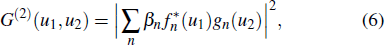 |
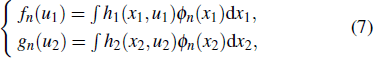 |
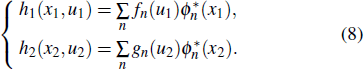 |
By using Eq. (
First, substituting Eq. (
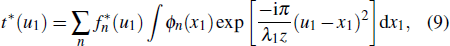 |

Then, substituting Eq. (
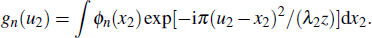 |
After considering the above equation, equation (
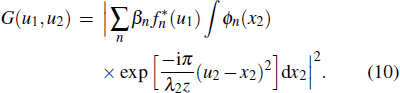 |
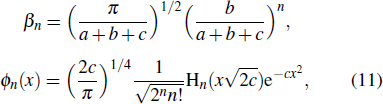 |

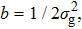
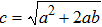
By comparing Eq. (
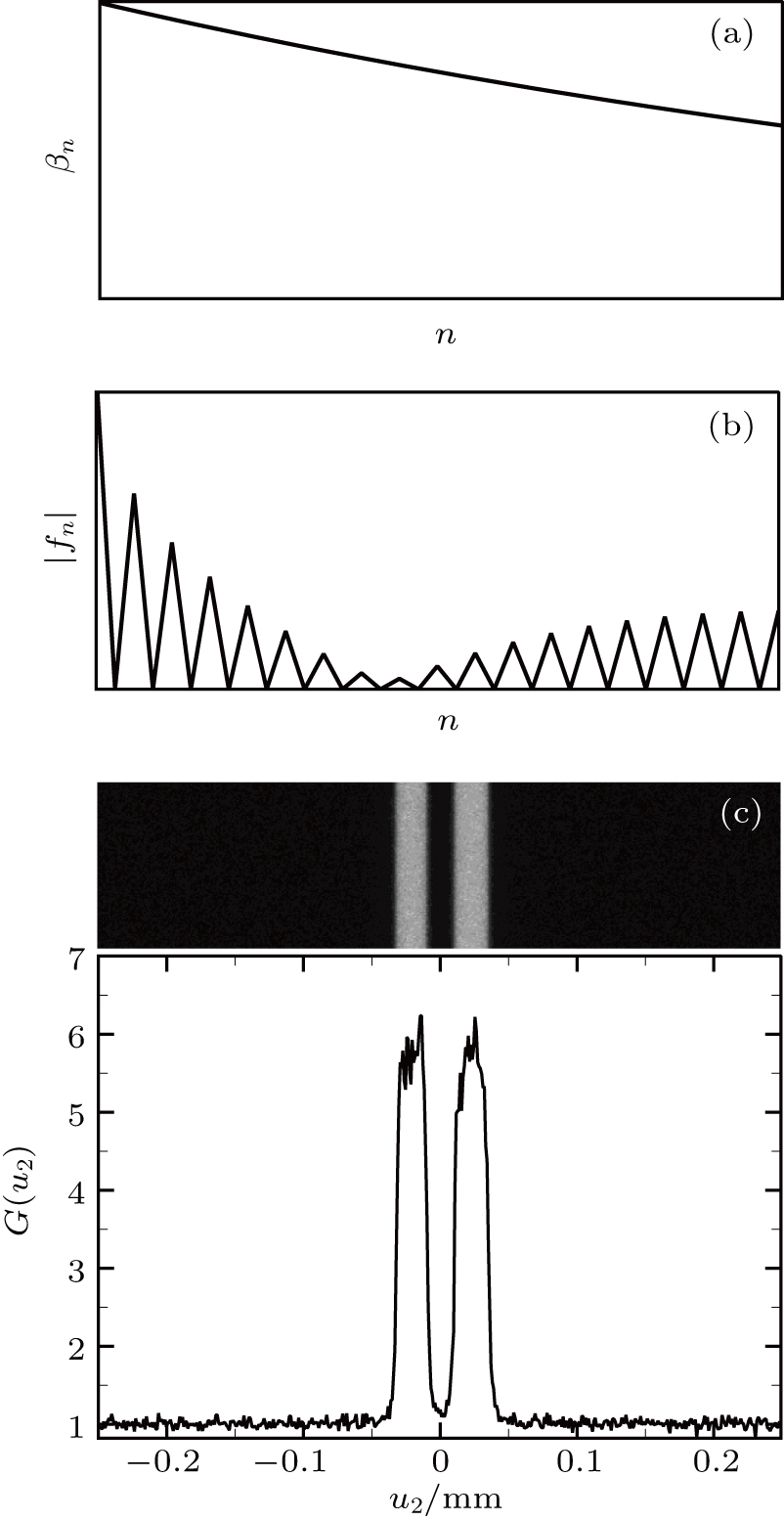
In this section, we give the numerical simulations to demonstrate the above analytical results. During the process, a double-slit with the slit width 0.08 mm and the distance between two slits 0.16 mm is chosen as the object imaged, and the parameters of light source are fixed as 
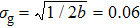
We firstly consider the case of the monochromatic light source λ1 = λ2 = 532 nm. Figures
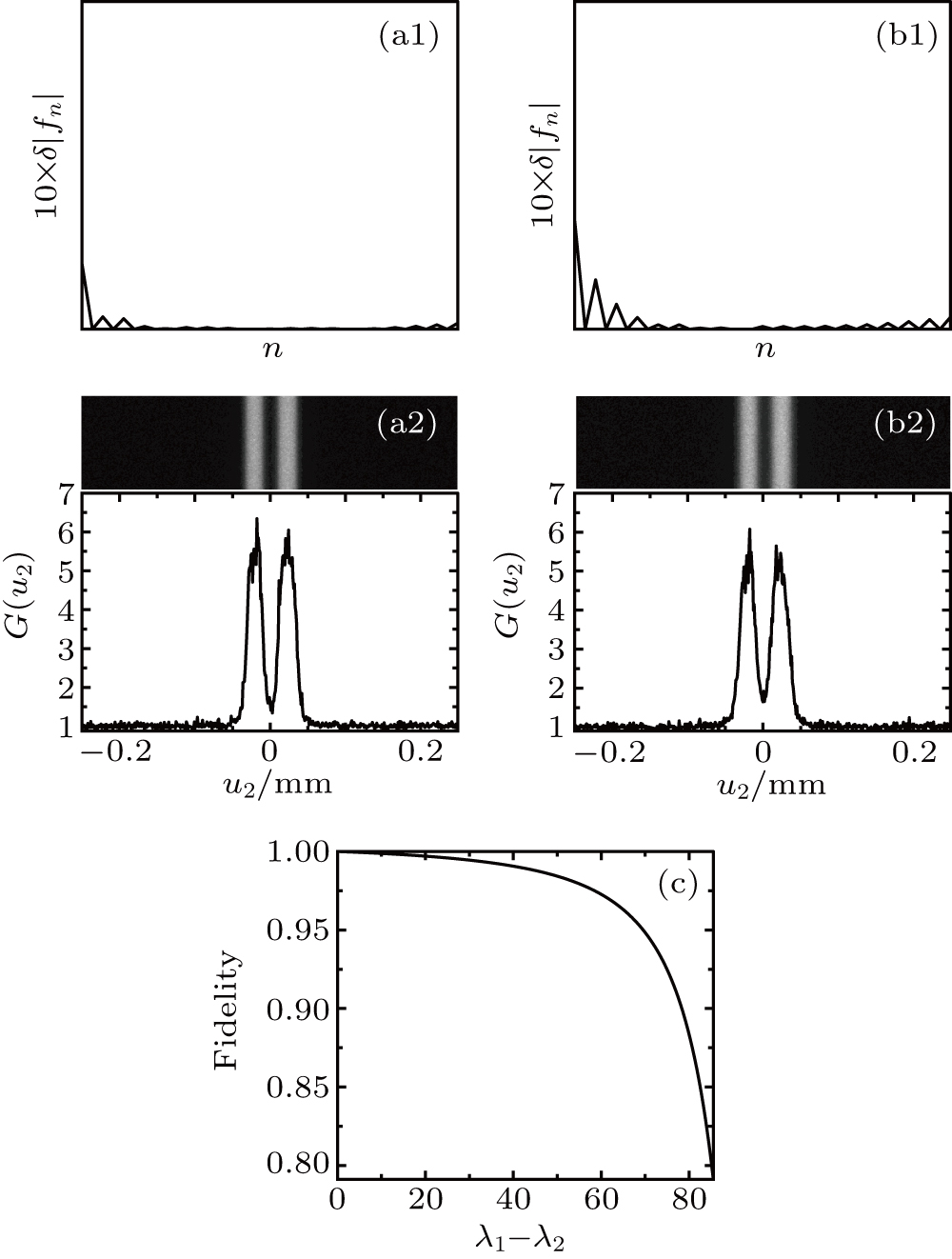
To show how two-color light source affects imaging quality when compared with the monochromatic light, we first change the wavelength in the object arm but keep the wavelength in the reference arm unchanged. Here we choose two different λ1 values 546 nm and 560 nm, and the corresponding results are shown in Figs.
To get a deeper insight into the effect from the wavelength change in the object arm on the imaging quality, we depict the dependence of the fidelity on the wavelength difference λ1–λ2 in Fig. 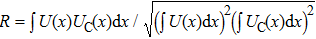
Then we analyze the effect from the wavelength of the light used in the reference arm, and the results are plotted in Fig.
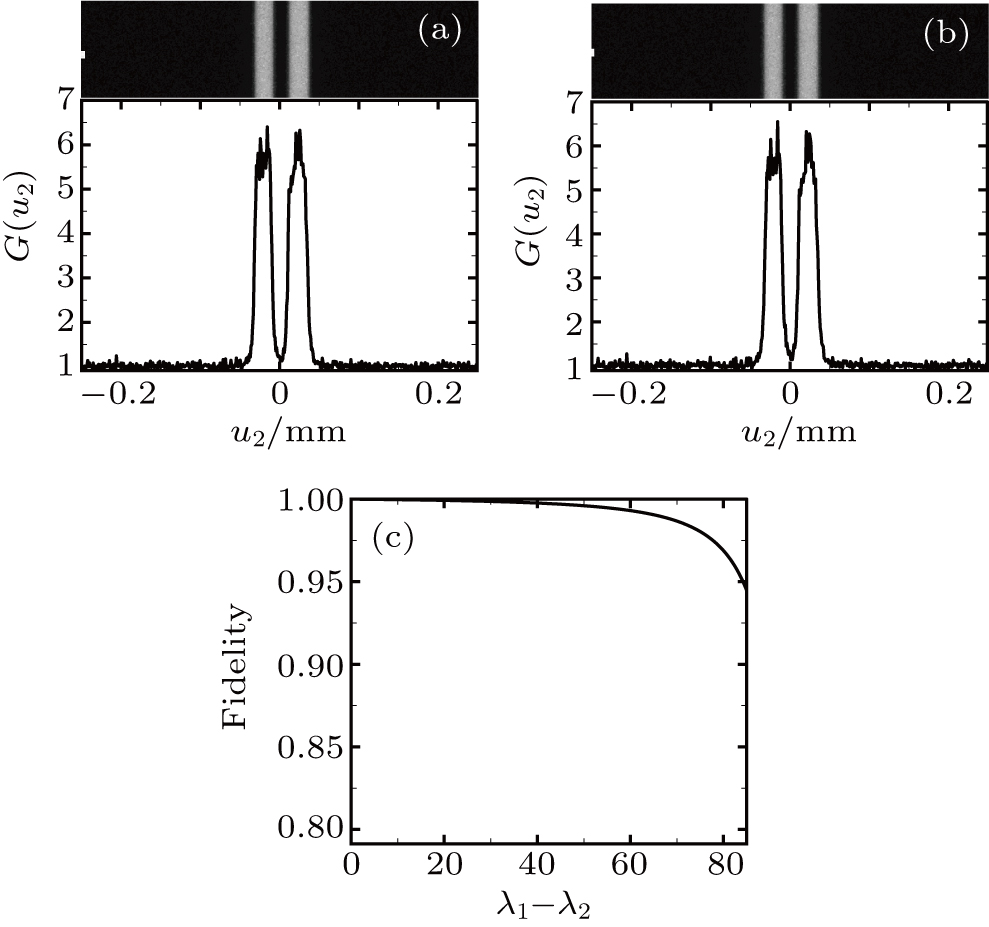 | Fig. 4. The reconstructed double-slit for (a) λ2 = 546 nm and (b) λ2 = 560 nm. Other parameters are the same as those in Fig. |
By comparing Figs.
We have investigated the possibility of analyzing imaging quality in a lensless two-color ghost imaging system by the coherent-mode representation theory. Unlike the integral representation theory under which one has to give a complicated expression of PSF to study which wavelengths has a bigger influence on imaging quality in a two-color ghost imaging, from the coherent-mode representation, one can investigate imaging quality of two-color ghost imaging by the distribution variety of the decomposition coefficients of the object which is caused by the wavelength changes. The analytical and numerical results show that the distribution variety of fn is only related to the wavelength in the object arm. In other words, imaging resolution depends primarily on the wavelength of the light illuminating the object. We also analyze the applicable condition of the coherent-mode representation theory. It should be emphasized that the two-color light source used in this paper is produced by using SLMS, and it is an artificial and controllable source. In other words, our results are not suitable for the true thermal light source.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |