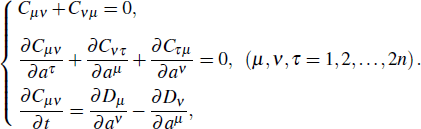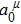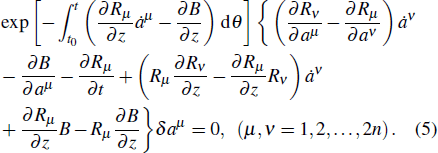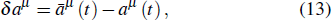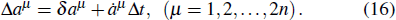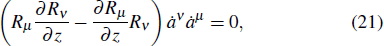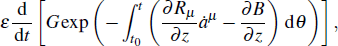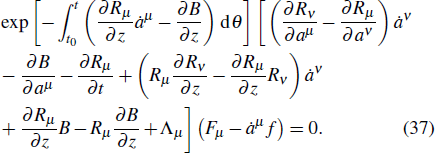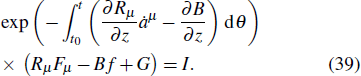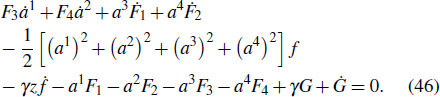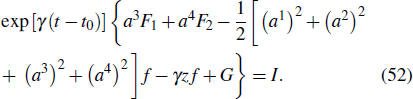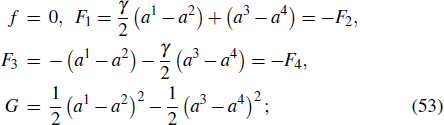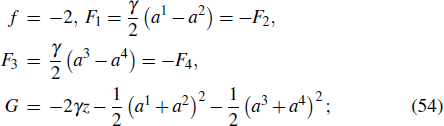1. IntroductionIt is well known that conservation laws play an important role in the study of complex dynamical systems. The existence of certain conserved laws is useful for us to find out the local physical properties and dynamical behaviors, even if the differential equations of motion are nonintegrable. By using conservation laws, the differential equations of motion can be reduced. What is more, conservation laws are also important in the stability analysis of dynamical systems. Therefore, the study of conservation laws has always been a hot topic in analytical mechanics.[1] In fact, there are many methods to find conservation laws of mechanical systems. The traditional method is to derive the cyclic integral and generalized energy integral directly from the differential equations of motion. In addition, conservation laws can be established by using the invariance of the action functional, the differential equations of motion, and the dynamical functions under the infinitesimal transformations, i.e., Noether conserved quantity,[2–6] Hojman conserved quantity,[7–10] and Mei conserved quantity.[11–14] Besides, the conservation laws can also be studied by the differential variational principle, such as the d’Alembert principle,[15] Jourdain’s principle,[16–19] Gauss’s principle,[19,20] and Pfaff–Birkhoff–d’Alembert principle.[20,21] In this paper, the conservation laws are constructed by the differential variational principle of Herglotz type.
The classical integral variational principles, such as the most famous Hamilton principle and Lagrange principle, are all extreme value problems of the action functional for a holonomic conservative system. For a non-conservative system, however, there is generally no action functional that makes its variation equal to zero. For example, the Hamilton principle of a holonomic non-conservative system, i.e.,
is not a principle of stationary action.
[22] In fact, it is a quasi variational principle.
Different from the classical variational principle above, the Herglotz variational principle[23] gives a variational description of a holonomic non-conservative system. The Herglotz variational principle can describe all physical processes that the classical variational principle can, and can be applied to solve non-conservative problems where the classical variational principle is not applicable. The action functional of the Herglotz variational principle is defined by a differential equation. If its Lagrangian or Hamiltonian does not depend on the action functional, the Herglotz variational principle reduces to the classical integral variational principle.
In recent years, the Herglotz variational principle and its symmetries have been applied in finite and infinite dimensional non-conservative dynamic systems, quantum systems, thermodynamics, optimal control theory, and other fields.[24–33] In Ref. [34], the simple and physically meaningful Lagrangians of Herglotz type were constructed, which describe a wide range of non-conservative classical and quantum systems, for example, vibrating string under viscous forces, non-conservative electromagnetic theory, non-conservative Schrödinger equation, non-conservative Klein–Gordon equation, etc.
American physicist Santilli[35] pointed out that Birkhoffian mechanics is the most general possible mechanics, which can be applied to hadron physics, space mechanics, statistical mechanics, biophysics, engineering, etc. Mei[36] proposed that Birkhoffian mechanics is a new stage in the development of analytical mechanics. Therefore, it is of great significance to study Birkhoffian mechanics.[37–40]
The sufficient and necessary conditions that the system of first-order differential equations
has a Birkhoffian representation are that the system satisfies the self-adjoint conditions
Therefore, it is difficult to convert a general holonomic non-conservative system or a nonholonomic system into a Birkhoffian system, while it is relatively easy to convert the system into a generalized Birkhoffian system.
[40] However, similar to the extension of the Hamilton principle to non-conservative systems, it is also difficult to extend the Pfaff–Birkhoff principle
to the generalized Birkhoffian system or to the constrained Birkhoffian system. The generalized Pfaff–Birkhoff principle
cannot be expressed as a variation of an action functional equal to zero.
On the basis of the Herglotz variational principle, we proposed the variational principle of the Birkhoffian system of the Herglotz type,[41,42] and established a variational description of the generalized Birkhoffian system, which can systematically deal with the Birkhoffian system and the generalized Birkhoffian system. When the Birkhoffian B and Birkhoff’s functions Rμ do not depend on the action functional, this principle reduces the classical Pfaff–Birkhoff principle.
In this paper, we propose a new differential variational principle, the Pfaff–Birkhoff–d’Alembert principle of Herglotz type, which provides a simple method to give variational descriptions of holonomic non-conservative processes and nonholonomic non-conservative processes in Birkhoffian systems. By use of the new differential variational principle, we will study the conservation laws for the Birkhoffian system and the constrained Birkhoffian system. At the same time, the inverse theorem of the conservation theorem will be given.
2. Pfaff–Birkhoff–d’Alembert principle of Herglotz typeThe variational problem for a Birkhoffian system of Herglotz type can be described as follows.[41]
Determine the functions aμ (t) satisfying the given boundary conditions
such that integral functional
z(
t) reaches its extreme at
t =
t1, i.e.,
where
z(
t) is defined by the differential equation
and satisfies the initial condition
Here,
B(
t,
aν(
t),
z(
t)) is the Birkhoffian of Herglotz type, and
Rμ (
t,
aν(
t),
z(
t)) are Birkhoff’s functions of Herglotz type.
aμ(
t) (
μ = 1, 2, …, 2
n) are Birkhoff’s variables, and
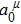
,

,

are constants.
The above extreme problem can be called the Pfaff–Birkhoff principle of Herglotz type.
A new type of differential variational principle can be derived from the Pfaff–Birkhoff principle of Herglotz type. To solve the above extreme problem, we can easily obtain[41]
Consider the arbitrariness of the integral interval [
t0,
t1], so
The principle (
5) is called the Pfaff–Birkhoff–d’Alembert principle of Herglotz type, which is a new differential variational principle.
3. Birkhoff’s equations of Herglotz typeMaking use of the Pfaff–Birkhoff–d’Alembert principle of Herglotz type, we can deduce Birkhoff’s equations of Herglotz type.
If δaμ (μ = 1, 2, …, 2n) in principle (5) are independent of each other, we have
The above equations are Birkhoff’s equations for the Birkhoffian system of Herglotz type.
If 2n Birkhoff’s variables aμ are not independent of each other, they are subject to 2m (m < n) constraints
Taking the calculation of the variation to formula (
7), we can obtain the restriction of constraints (
7) on the virtual displacements
From principle (
5) and restriction (
8), and by using the usual Lagrange multiplier method, we obtain
where
λβ are the constraint multipliers. The above equations are Birkhoff’s equations for the constrained Birkhoffian system of Herglotz type.
4. Isochronal variation and nonisochronal variationThe isochronal variation and nonisochronal of the variables aμ respectively are
Since the variation Δ
t is small enough, making expansion

and keeping the first order items, we have
From formulae (
13)–(
15), we easily obtain
Introducing the infinitesimal generators of space Fμ and the infinitesimal generators of time f, we have
Thus, we can obtain
where
ε is an infinitesimal parameter.
5. The conditions of the invariance for the Pfaff–Birkhoff–d’Alembert principle of Herglotz typeSubstituting Eq. (18) into Eq. (5), we obtain
Considering
we can rewrite formula (
19) as
On the left hand side of Eq. (
24) plus and minus the function
we obtain
where
G =
G(
t,
aμ,
z) is a gauge function. Equation (
22) is the transformation of the condition of the invariance for the Pfaff–Birkhoff–d’Alembert principle of Herglotz type, or the deformation of the Pfaff–Birkhoff–d’Alembert principle of Herglotz type under infinitesimal transformations.
6. Conserved quantity for a Birkhoffian system of Herglotz typeAccording to Eq. (25), if there exists a gauge function G, which can make the infinitesimal generators of space Fμ and the infinitesimal generators of time f satisfy the following conditions:
then the system has a conserved quantity, which can be written in the following form
So we can draw the following conclusion.
7. Conserved quantity for a constrained Birkhoffian system of Herglotz typeSubstituting Eq. (18) into Eq. (8), and taking note of the arbitrariness of the parameter ε, we have
which are the restriction of the constraints (
7) on the infinitesimal generators
Fμ and
f.
By Eqs. (7) and (9), we can obtain the constraint multipliers λβ, which are the functions of t, aμ, and z. Then, substituting them into Eq. (9), we have
where
Equations (
31) are called Birkhoff’s equations of the free Birkhoffian system corresponding to the constrained Birkhoffian system (7), (9) of Herglotz type, for short, Birkhoff’s equations of the corresponding free Birkhoffian system. If the initial conditions satisfy the constraint of Eq. (
7), then the solution of Eq. (
31) gives the motion of the constrained Birkhoffian system.
Similar to Theorem 1, we have the following theorem.
Substituting the restriction Eq. (30) into formula (33), we can obtain formula (26). Therefore, we derive the following theorem.
8. Inverse theorems of conservation theoremsFor the constrained Birkhoffian system (7), (9) of Herglotz type, assume the system has a conserved quantity
Differentiating both sides of formula (
33) with respect to time
t, we obtain
Multiplying the two sides of Eq. (
31) by

, we have
Add Eqs. (
36) and (
37), and let the coefficients of

be zero. Obviously, the items containing

are equal to zero, so we have
Then, let the integral (
35) be equal to the conserved quantity (
27), i.e.,
Thus, we draw the following conclusion.
If the constraints do not exist, from Theorem 5, we obtain the inverse theorem of the conservation theorem for the Birkhoffian system of Herglotz type as follows.
9. ExampleConsider a fourth-order Birkhoffian system of Herglotz type, whose Birkhoffian and Birkhoff’s functions are
Supposing the constraints of this system are
we try to study its conserved quantity.
By Eq. (9), we have
From Eq. (
44) and the constraints (
42), (
43), we obtain
The conditions (
26) give
According to the restriction Eq. (
30), we have
The solution of Eq. (
46) is
Obviously, the generators
Fμ and
f given by formula (
49) satisfy Eqs. (
47) and (
48). Therefore, we obtain the conserved quantity by Theorem
1 as
Next, by Theorem 5 and a given conserved quantity, we can obtain the corresponding infinitesimal generators. Assume there is a quantity (50) of this system, from formula (38), we obtain
Formula (
39) gives
Equations (
51) and (
52) have the solutions
Taking note of constraints (
42) and (
43), generators (
53), (
54), and (
55) all satisfy the restriction of Eqs. (
47) and (
48). Therefore, they are the infinitesimal generators and the gauge function for the constrained Birkhoffian system of Herglotz type.
10. ConclusionThe Pfaff–Birkhoff–d’Alembert principle of Herglotz type, a new differential variational principle, is proposed. Birkhoff’s equations for the Birkhoffian system (6) and the constrained Birkhoffian system (9) of Herglotz type are obtained, respectively. Not only are the conservation theorem and its inverse theorem for the Birkhoffian system of Herglotz type (6) established, but also the ones for the constrained Birkhoffian system of Herglotz type (9) are given. When the gauge function G = 0, the conservation theorems and inverse theorems become the conclusions of Ref. [41]. On the other hand, according to the relationship among Lagrangian systems, Hamiltonian systems, and Birkhoffian systems, the conservation theorems of this paper can reduce to the ones for the Lagrangian system or the Hamiltonian system of Herglotz type when Birkhoffian B and Birkhoff’s functions Rμ are taken to some special values. Consequently, the results of this paper are more general and can even solve the problems of nonholonomic systems.