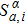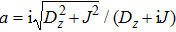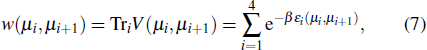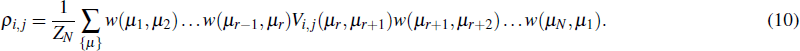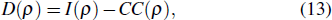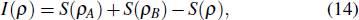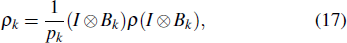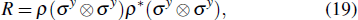1. IntroductionQuantum correlations play an important role in understanding the fundamental characteristics of quantum systems, and have been exploited to realize some tasks in quantum information.[1–4] As the most frequently used form of quantum correlations, quantum entanglement has been intensively studied both theoretically and experimentally.[5–12] In addition to quantum entanglement, quantum discord is another kind of quantum correlation and has drawn a great deal of attention in recent years. Quantum discord was first introduced by Ollivier and Zurek in 2001, and they defined the difference between the two classically identical expressions of the mutual information as quantum discord.[13] The calculation process of quantum discord needs to involve the optimization over all possible measurements on one system, so it is extremely difficult to obtain analytical solutions except some particular cases.[13–19] Recently, Ali et al. have deduced the analytical formula for a two-qubit X state depending on seven real-valued parameters.[16] Quantum discord has shown its advantage in quantum information processing and quantum computation, thus an enormous amount of effort has been devoted to studying the quantum discord.[20–29] For practical significance, many researches have focused on the behaviors of quantum correlations at finite temperature. Thermal entanglement (TE) and thermal quantum discord (TQD) are two useful tools in characterizing quantum correlations of the system at finite temperature.[30,31] Heisenberg spin chain as a simple quantum system has been intensively studied on TE and TQD.[22,32–37]
The diamond Heisenberg spin chain is an interesting model in the studies of the Heisenberg spin chains. The experimental results showed that the natural mineral azurite Cu3(CO3)2(OH)2 could be regarded as an actual material for the frustrated diamond chain.[38,39] Due to the mathematical difficulties of the rigorous theoretical treatment of geometrically frustrated quantum Heisenberg diamond chains, a simplified model called the Ising–Heisenberg diamond chain was proposed.[40–42] It is noted that the Ising–Heisenberg diamond chains have also attracted a great deal of attention in the study of TE and TQD recently.[24,43–46] Rojas et al. investigated TE in an infinite spin-1/2 Ising–XXZ diamond chain.[44] Based on the same model, Gao et al. studied quantum phase transitions characterized by TQD.[24] Dzyaloshinsky–Moriya (DM) interaction, as a kind of antisymmetric anisotropic superexchange interaction, was first introduced by Dzyaloshinsky[47] and Moriya[48] to mainly explain the phenomenon of weak ferromagnetism in antiferromagnetic crystals. It has been found that DM interaction can induce unusual magnetic properties in some antiferromagnetic materials. Additionally, it has also been shown that DM interaction plays an important role in TE and TQD of a Heisenberg spin chain.[22,32,49] Chen et al. investigated TQD in a Heisenberg XXZ model with DM interaction, and found that the region of TQD can be effectively controlled via regulating the DM interaction parameter.[49] In the study of the azurite with the diamond Heisenberg spin chain, the important influences of DM interaction on the ordered magnetic moment structure and the magnetic anisotropy of the azurite have been analyzed and discussed.[50–52] Motivated by the importance of DM interaction in the azurite, in this paper we will focus on the effect of DM interaction on the properties of thermal quantum correlations in an infinite spin-1/2 Ising–Heisenberg diamond chain. TQD and TE as two kinds of important methods to measure quantum correlation will be discussed, respectively. We will apply concurrence[53] to measure the entanglement of the system, and use the explicit expressions for quantum discord developed by Ali et al.[16] to characterize TQD.
The rest of the paper is organized as follows. We introduce the model and the calculations of quantum discord and concurrence in Section 2. Section 3 is devoted to illustrating the effects of DM interaction on the behaviors of TQD and TE at finite temperature. Our conclusion is given in Section 4.
2. Model and methodThe Hamiltonian of an infinite spin-1/2 Ising–Heisenberg diamond chain with DM interaction in an external magnetic field is given by
with
where
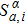
,

(
α =
x,
y,
z), and

represent the relevant components of the spin-1/2 operator. The parameter
J stands for the interaction strength between the nearest-neighboring Hesienberg spins, and the parameter
J1 corresponds to the interaction between the nearest-neighboring Ising and Heisenberg spins.
J > 0 and
J1 > 0 represent the antiferromagnetic coupling.
Δ represents the anisotropy parameter,
Dz is the strength of DM interaction in the direction of
z, and
h is the external magnetic field. The schematic of the spin-1/2 Ising–Heisenberg diamond chain is illustrated in Fig.
1. For convenience, the periodic boundary condition (
μN + 1 =
μ1) will be considered in the following discussion.
By assuming fixed values for μi and μi + 1 and diagonalizing the block Hamiltonian
 , we can obtain the following eigenvalues depending on the Ising spins:
, we can obtain the following eigenvalues depending on the Ising spins:
The corresponding eigenstates based on the standard basis {|00⟩, |01⟩, |10⟩, |11⟩} are given by
where
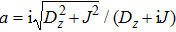
. It is necessary to confirm the commutation relation

for
i ≠
j, which allows us to adopt the transfer matrix method to gain the TQD and TE of this infinite chain.
[24,44] By performing the trace over the states of Heisenberg spins, the partition function can be written as
[44]
with
W being a 2 × 2 transfer matrix
where indices ±1/2 denote two spin states of the classical Ising spins
μi = ±1/2. The element of transfer matrix is
where

is a 4 × 4 matrix, named two-qubit operator, and
β = 1/(
kBT) (
kB is the Boltzmann’s constant that we will henceforth take equal to 1, and
T is the temperature. The parameter
J1 is taken as unit temperature
T. In the following numerical calculation, we let
J1 = 1.). Afterwards the partition function can be rewritten as
where
λ1 and
λ2 are the eigenvalues of the transfer matrix in Eq. (
6), and we suppose
λ1 >
λ2. In the thermodynamic limit
N → ∞, the contribution of a smaller transfer-matrix eigenvalue to the partition function can be ignored, then equation (
8) becomes
By means of the transfer matrix approach, we can write the element of the reduced density operator as[44]
After a series of algebraic operations, in the thermodynamic limit the element of the reduced density operator of an infinite spin-1/2 Ising–Heisenberg diamond chain can be obtained
[44]
where

, and
Vi, j is the element of the two-qubit operator. Running all possible
i and
j, the reduced density matrix has the following expression:
Based on the reduced density matrix in Eq. (12), we can calculate TQD and TE. Firstly, we review the concept of quantum discord, which is defined as the difference between the mutual information and the classical correlation,[13,14]
where
I(
ρ) is the mutual information expressed as
where
S(
X) = −Tr(
Xlog
2X) is the von Neumann entropy.
ρA and
ρB are reduced density matrices of two Heisenberg spins in the
ith block respectively.
CC(
ρ) is the classical correlation
where
S(
ρ|{
Bk}) is the quantum conditional entropy with respect to the von Neumann type measurement {
Bk} performed locally only on subsystem B, and it can be defined as
where the conditional density operator is
and
pk = Tr[(
I⊗
Bk)
ρ(
I⊗
Bk)].
Next, we use the concurrence to measure the TE of the diamond chain. The concurrence can be defined as[53,54]
with the quantities
ei (
e1 ≥
e2 ≥
e3 ≥
e4) are the eigenvalues of the operator
where
ρ* is the complex conjugate of the reduced density matrix
ρ given by Eq. (
12), and σ
y is the Pauli operator.
3. Results and discussionThe first derivative of the quantum discord can manifest the quantum critical point (QCP) at a finite temperature.[24] The QCP is a special point at which the ground state of the system abruptly becomes another one by adjusting the parameters of the system. Firstly, we investigate the effect of DM interaction on the QCP. The variations of TQD and the corresponding first derivatives with the anisotropy parameter Δ for different temperatures and DM interaction are plotted in Fig. 2. In order to compare with the previous results given by Gao et al.,[24] we set the parameters h = J = J1 = 1, T = 0.03, 0.05, 0.1, and 0.15, and Dz = 0.5, 1, and 1.5. It is shown that when the anisotropy parameter Δ increases to a certain value, the value of TQD abruptly changes from 0 to the maximum, as shown in Figs. 2(a), 2(c), and 2(e), which is consistent with the previous result.[24] Then the maxima of the corresponding first derivative reflect the QCP in Figs. 2(b), 2(d), and 2(f). Interestingly, it is found that the QCP moves to the left of the axis as the value of Dz increases. It indicates that the inclusion of DM interaction would reduce the anisotropy parameter value required to achieve QCP. For instance, when Dz = 0.5, the QCP occurs at Δ = 0.88 from Figs. 2(a) and 2(b), while when Dz = 1 and 1.5, the QCP occurs at 0.58 and 0.19, respectively.
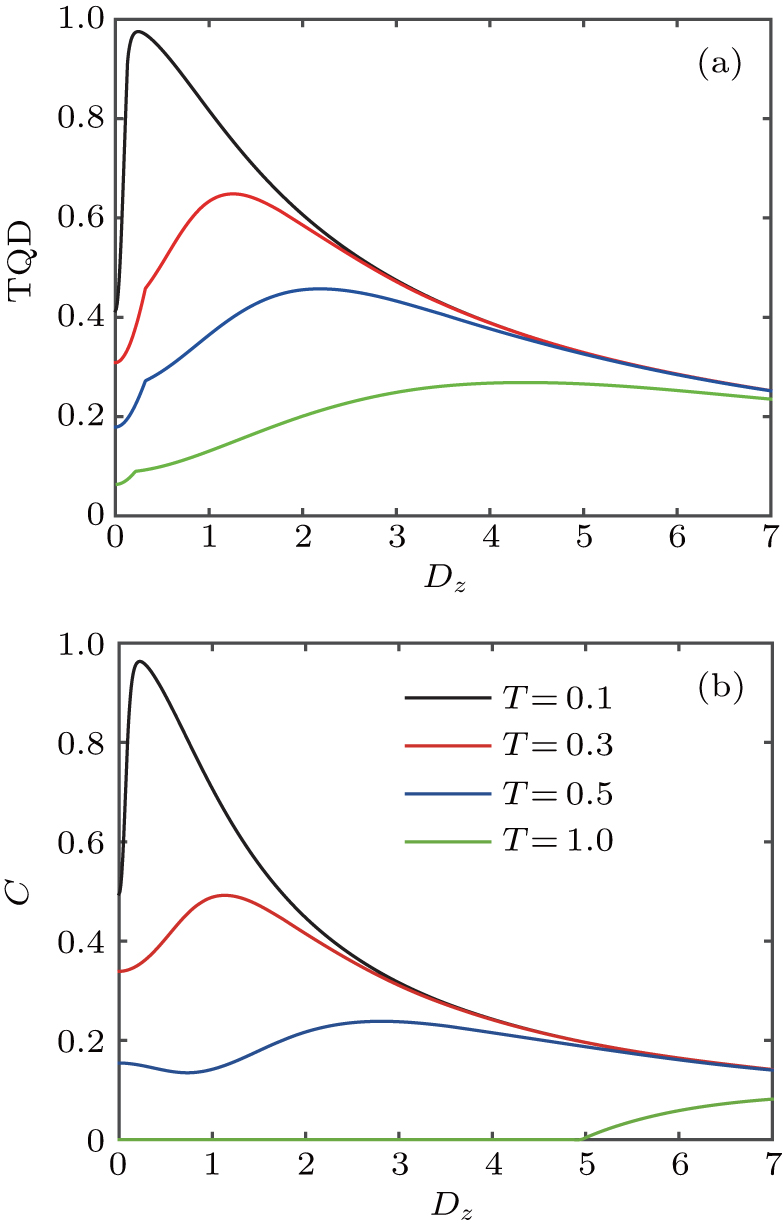
TQD and concurrence C as a function of DM interaction Dz with fixed parameter values (Δ = 1, J1 = 1, h = 1, and J = 1) for different temperatures are shown in Fig. 3. It is noted that DM interaction is a weak interaction, but in order to explore the effect of DM interaction on the quantum correlation at different temperatures, we take the value of Dz up to 7. From Fig. 3(a), it is found that at low temperature (e.g. T = 0.1), as Dz increases, TQD increases sharply to a maximum and then gradually decreases. With the temperature increasing, the maximum of TQD decreases, moreover, the value of DM interaction Dz at which TQD is the maximum increases. For instance, when T values are 0.1, 0.3, 0.5, and 1.0, the maxima of TQD are 0.9753, 0.6484, 0.4573, and 0.2687, and the corresponding Dz’s are at 0.24, 1.24, 2.17, and 4.32, respectively. Furthermore, it is observed that when DM interaction Dz is large enough, as the temperature increases, the value of TQD keeps unchanged at the same Dz parameter. In Fig. 3(b), it is shown that the variation behavior of concurrence C with Dz is similar to that of TQD. However, at a finite temperature, the suppression of temperature on concurrence is more striking than TQD. For instance, for Dz = 1.5, when T values are 0.3, 0.5, and 1.0, the corresponding TQD values are 0.6386, 0.4272, and 0.1666, while concurrence C values are 0.4719, 0.1793, and 0, respectively.
For different DM interaction parameters, the ranges of the threshold temperature and the external magnetic field at which quantum correlations vanish are shown in Fig. 4. The areas surrounded by the curves and the coordinate axis present the occurrence of quantum correlations. Here we assume that there is no corresponding quantum correlation when TQD or C is less than 0.01 in the numerical calculation. In Fig. 4(a), it clearly shows that the area where TQD exists increases with the increase of the DM interaction. It implies that the enhancement of Dz can increase the threshold temperature Tc and external magnetic field hc. For instance, when Dz = 0 and 1, Tc = 2.83 and 3.87, hc = 5.12 and 6.24, respectively. It is interesting to find that there are two threshold temperatures within some certain threshold external magnetic field. For instance, in the case with Dz = 1 and hc = 5.84, TQD vanishes until T increases up to 1.31, and will occur in the region of 1.31 ≤ T ≤ 2.67, then disappears again when T > 2.67. Figure 4(b) exhibits the regions where concurrence exists with different DM interaction parameters. It is found that the variations of Tc and hc with Dz are nonmonotonic. Similar to Fig. 4(a), there are two threshold temperatures for some certain threshold external magnetic field. Comparing Fig. 4(a) with Fig. 4(b), it is found that for the same Dz value, Tc and hc of TQD are larger than those in Fig. 4(b), which indicates that TQD contains more information of quantum correlation than the concurrence.
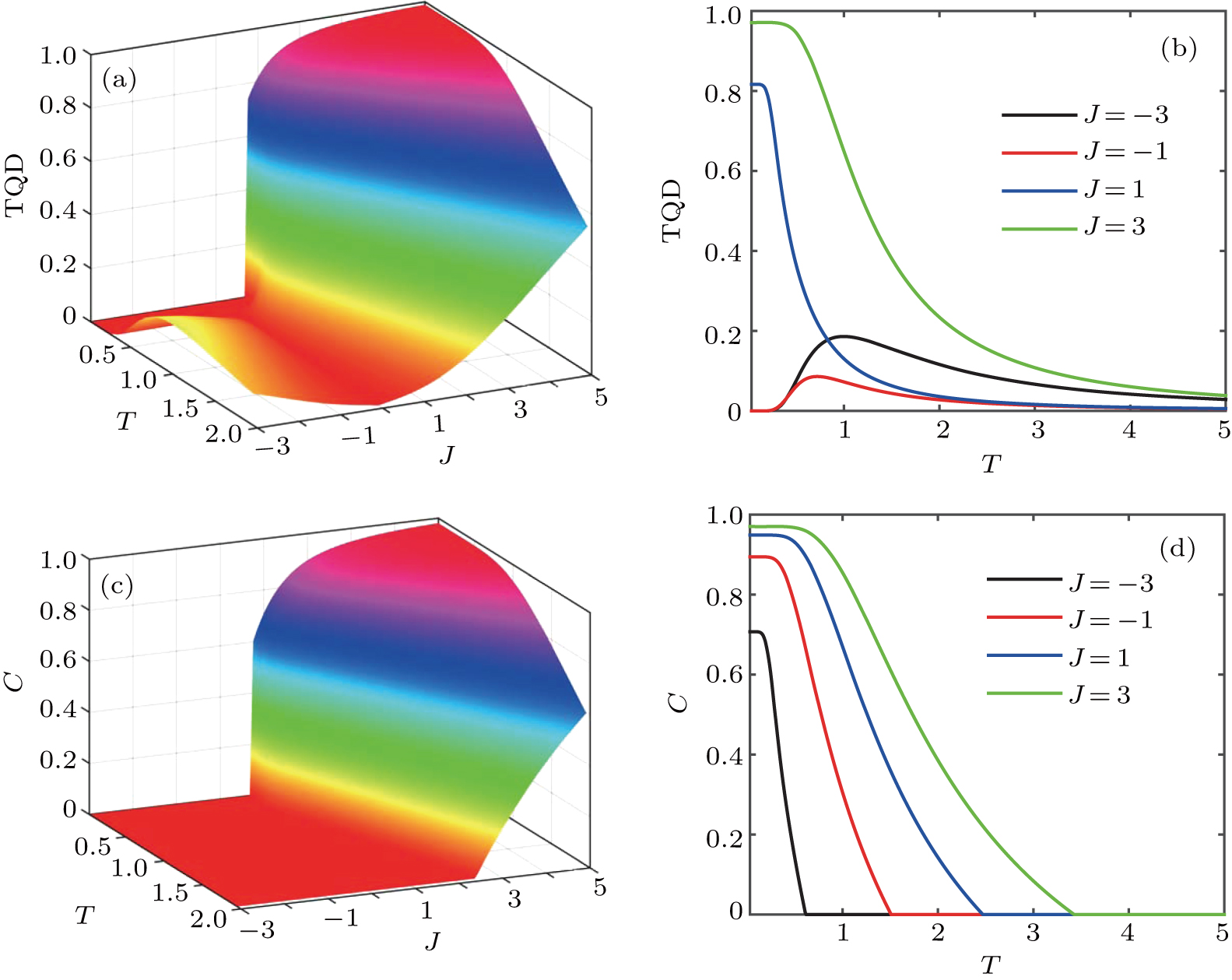
Next we study the effects of temperature T and the Heisenberg coupling parameter J on the Ising–XXX (Δ = 1) model with DM interaction. Figure 5 shows TQD and C versus T and J, where we set Dz = 1, J1 = 1, and h = 1. In the antiferromagnetic coupling case (i.e., J > 0), as shown in Figs. 5(a) and 5(c), the variation of TQD with temperature T is similar to the concurrence C. As the temperature increases from zero, the quantum correlations remain the maximum within a certain temperature range, but when the temperature exceeds the range and gradually increases, the quantum correlations are gradually weakened until they disappear. Moreover, the temperature range of the maximum quantum correlation increases with the increase of J. For instance, the blue (J = 1) and green (J = 3) lines in Fig. 5(b) as well as four lines (J = 1, 2, 3, and 4) in Fig. 5(d) correspond to the antiferromagnetic coupling case. Comparing Fig. 5(b) with Fig. 5(d), it is shown that TQD has advantage in against decoherence over concurrence C. For instance, when J = 1, the threshold temperature of TQD is obviously greater than that of C. Additionally, the increase of J enables the system to obtain a stronger quantum correlation and a greater threshold temperature. In Fig. 5(d), for instance, at T = 0.2, when J = 1, 2, 3, and 4, the concurrence C is 0.6744, 0.8942, 0.9487, and 0.9701, respectively.
Now we move to the case of J < 0. Apparently, from Figs. 5(a) and 5(c), it can be seen that the variation of TQD with temperature T is different from the concurrence C for J < 0. For the TQD, as shown in Fig. 5(a), an intriguing phenomenon called the “regrowth” behavior[23,24] occurs in the case of J < 0, while the concurrence C vanishes for J < 0 in Fig. 5(c). For instance, the “regrowth” behaviors are presented well by the black (J = −3) and red (J = −1) lines in Fig. 5(b). TQD is zero at low temperature, but it will increase to the maximum then decrease gradually to zero as T increases. It verifies the phenomenon of two threshold temperatures shown in Fig. 4(a). Moreover, the maximum of TQD increases with the absolute value of J increasing, for instance, when J = −1 and −3, the corresponding maxima of TQD are 0.08608 and 0.1862, respectively.
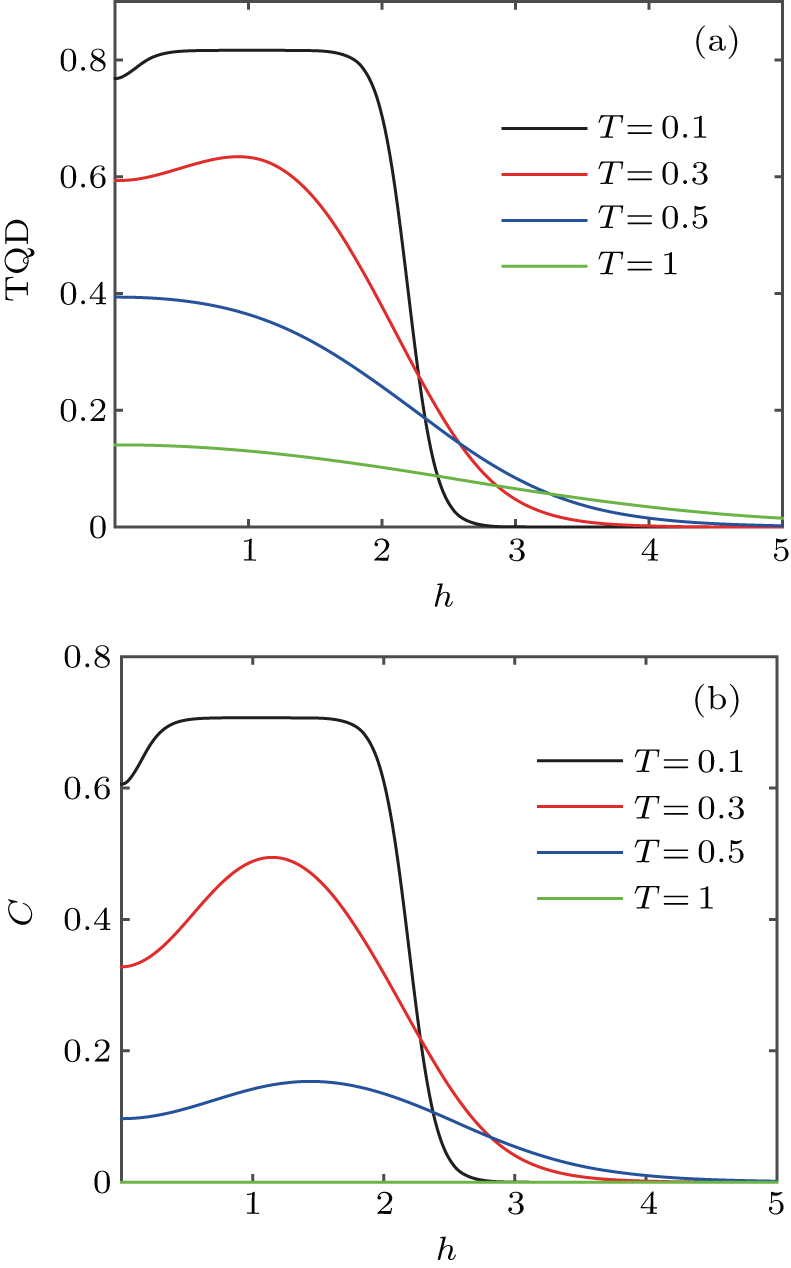
Figure 6 illustrates TQD and C as a function of the external magnetic field h for different temperatures with fixed values Δ = 1, J1 = 1, Dz = 1, and J = 1. In Fig. 6(a), the variation of TQD with h exhibits a nonmonotonous behavior at low temperature (e.g. T = 0.1 and 0.3). For instance, at T = 0.3, when h = 0, TQD is equal to 0.5935. As h increases, TQD increases gradually to a maximum of 0.6344 at 0.9 ≤ h ≤ 0.93, then it decreases gradually to zero. However, for higher temperature (e.g. T = 0.5 and 1), the monotonous variation of TQD with h is shown in Fig. 6(a). With h increasing, TQD decreases gradually to zero. The nonmonotonous variations of concurrence C with h at low temperature are also observed (see T = 0.1, 0.3, and 0.5 in Fig. 6(b)). For instance, at T = 0.3, when h = 0, concurrence C = 0.3278. With the increase of h, concurrence increases gradually to a maximum of 0.4945 at 1.14 ≤ h ≤ 1.16, then it decreases gradually to zero. Furthermore, comparing Fig. 6(a) with Fig. 6(b), it can be seen that TQD is more robust against the effect of temperature than the concurrence. For instance, when T = 0.5 and h = 1, TQD is 0.3643 while C = 0.1418.
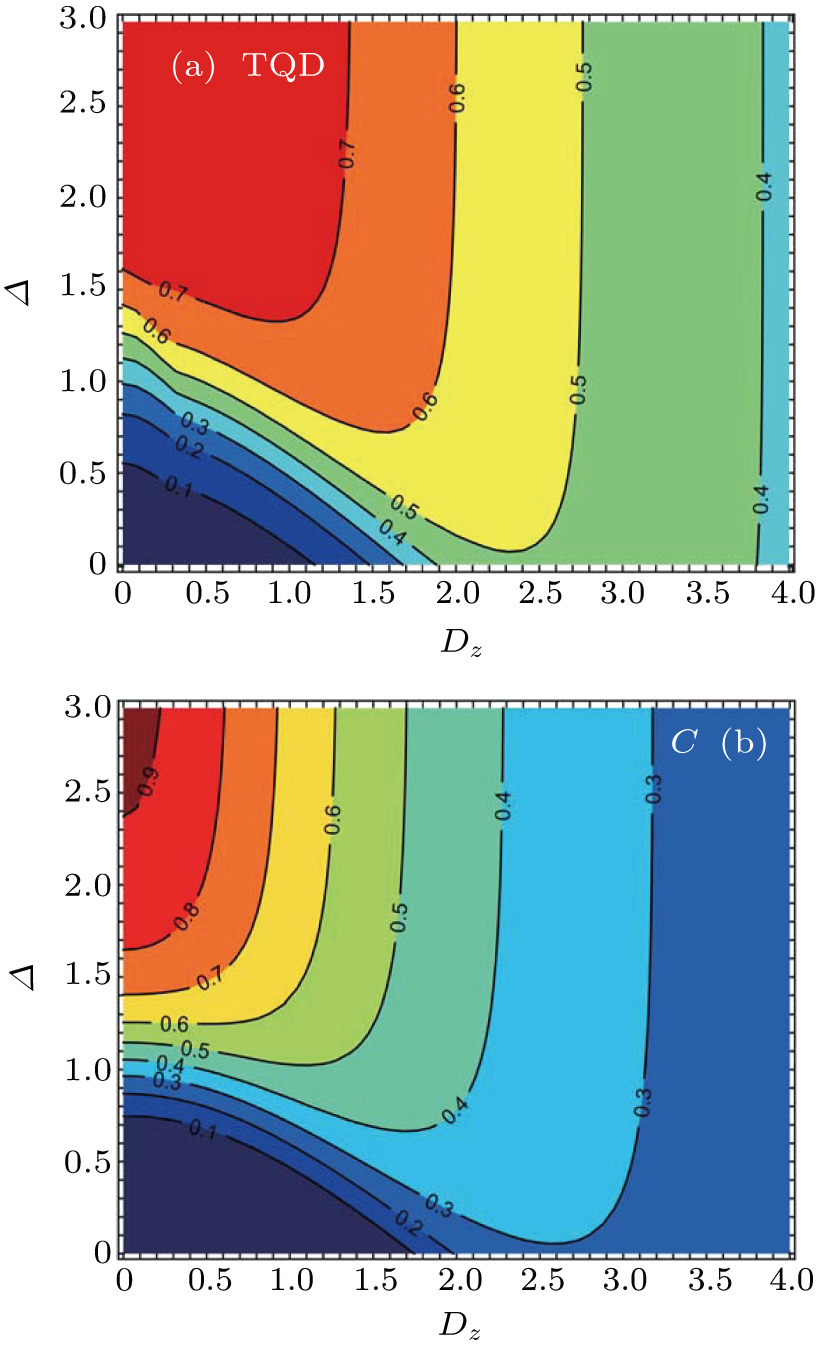
Finally, we plot the isoline maps of TQD and concurrence C with Δ and Dz in Figs. 7(a) and 7(b), respectively. In Fig. 7, different colors represent the range of different values of quantum correlation, and the values of isoline are marked in the maps. It is shown that Δ and Dz play an important role in both cases. When the DM interaction of the system is weak, the system can get a stronger quantum correlation by increasing the anisotropy Δ. On the other hand, when Dz is large enough, the quantum correlations keep unchanged with Δ increasing. Moreover, it is also found that the quantum correlations of the system will increase first and then decrease with the increase of Dz within a certain range of Δ, which is consistent with the conclusion of Fig. 3.
4. ConclusionIn this paper, we apply TQD and TE to investigate the thermal quantum correlations of the Ising–Heisenberg diamond chain with DM interaction. Firstly, we use TQD as the measurement to discuss the influence of DM interaction on the system’s QCP. Compared with the previous work, it is shown that DM interaction can decrease the value of anisotropy parameter Δ required to achieve QCP. Secondly, we investigate the behavior of thermal quantum correlations in the model of an Ising–XXX Heisenberg diamond chain by changing the temperature, Heisenberg coupling parameter, DM interaction, and external magnetic field. When the system is in an antiferromagnetic coupling case, the temperature will suppress the occurrence of the quantum correlations, but a certain strength of magnetic field and DM interaction will promote the quantum correlations. In a ferromagnetic coupling case, TQD shows the “regrowth” behavior while TE does not. Additionally, we also give the phase diagrams of the threshold temperature and magnetic field of an isotropic antiferromagnetic system with different DM interactions. DM interaction improves the values of threshold temperature and magnetic field for the measurement of TQD, while it only improves the value of threshold magnetic field but reduces the value of threshold temperature in the case of TE. Furthermore, it is also shown that TQD is more robust against decoherence than TE. Finally, we consider the effect of anisotropy Δ on quantum correlations of the system. For weak DM interaction, the increase of anisotropy can promote quantum correlations of the system.