† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11671244), the Higher School Doctoral Subject Foundation of Ministry of Education of China (Grant No. 20130202110001), and Fundamental Research Funds for the Central Universities, China (Grant No. 2016CBY003).
In this paper, we discuss quantum uncertainty relations of quantum coherence through a different method from Ref. [52]. Some lower bounds with parameters and their minimal bounds are obtained. Moreover, we find that for two pairs of measurement bases with the same maximum overlap, quantum uncertainty relations and lower bounds with parameters are different, but the minimal bounds are the same. In addition, we discuss the dynamics of quantum uncertainty relations of quantum coherence and their lower bounds under the amplitude damping channel (ADC). We find that the ADC will change the uncertainty relations and their lower bounds, and their tendencies depend on the initial state.
In quantum theory, the uncertainty relation is a fundamental consequence of the superposition principle and the incompatible nature of observables. The uncertainty relation is a powerful tool in many quantum information tasks, such as quantum key distribution,[1,2] quantum random number generation,[3,4] entanglement witness,[5] and Einstein–Podolsky–Rosen (EPR) steering.[6,7] The original formulation of this concept was given by Heisenberg in 1927,[8] and then further generalized by Robertson[9] for two arbitrary observables in 1929, in which a lower bound of total variance of two observables was given. Such an uncertainty relation based on variance generally relies on the definition of observables. Deutsch[10] and Maassen et al.[11] proposed an uncertainty relation based on the Shannon entropy of measurement outcomes. Moreover, the majorization entropic uncertainty relation[12] and the strong majorization entropic uncertainty relation[13] were considered based on the Rényi entropy and Tsallis entropy of the measurement outcomes by using the majorization technique. Kurzyk et al. discussed entropic uncertainty relations in terms of the Tsallis entropies for states with a fixed amount of entanglement.[14] Several other discussions on the uncertainty relation have been published.[15–19]
Quantum coherence is one of the most important physical resources in quantum mechanics, which can be used in quantum optics,[20] quantum information and quantum computation,[21] thermodynamics,[22,23] and low temperature thermodynamics.[24–26] Many considerable efforts have recently been made to quantify the coherence of quantum states from the perspective of resource theory.[27–50] The authors of Ref. [27] proposed a rigorous framework to quantify coherence. Consequently, various coherence measures have been defined based on this framework, such as l1-norm of coherence,[27] relative entropy of coherence (REOC),[27] quantum coherence via skew information (SIC),[28] and the geometric coherence (GC).[29]
As quantum coherence is a basis-dependent notion, we may ask if coherence respects some uncertainty relations for two or more incompatible bases. A concept of quantum uncertainty relation of quantum coherence was proposed in Refs. [51]–[53], and the sum of quantum coherence based on two measurement bases was called the quantum uncertainty relation of quantum coherence. Generally, the uncertainty relation of a measurement contains classical (predictable) and quantum (unpredictable) parts that originate from classical noise and quantum effect, respectively.[54] The quantum uncertainty relation of quantum coherence was considered as a quantum part (or genuine quantum uncertainty relation).[52] For the qubit case, quantum uncertainty relations based on two measurement bases were considered by using REOC, l1 norm of coherence, and coherence of formation.[52] They gave the lower bounds of the sum of the quantum coherence for a qubit state based on two measurement bases. These bounds are related to the maximum eigenvalue of the state and the maximum overlap of the two measurement bases. However, one will want to know the following question. (i) For a fixed single qubit state and two pairs of measurement bases which have the same maximum overlap, will they give the same lower bound? In the first place of this work, we try to answer this question. We first consider quantum uncertainty relations of the quantum coherence through a different method from Ref. [52]. We will obtain some lower bounds with parameters, and their minimal bounds. Moreover, we can find that for two pairs of measurement bases which have the same maximum overlap, the quantum uncertainty relations and lower bounds with parameters are different, but the minimal bounds are the same.
Any quantum system inevitably suffers from environmental effect. Therefore, it is important to investigate how the noisy environment influences the entropic uncertainty. Dynamics of the entropic uncertainty relations under noisy channels were explored.[55–58] Naturally, we believe that it is also important to investigate another question, i.e., (ii) how does the noisy environment influences the quantum uncertainty relation of the quantum coherence? In the next place of the paper, we will consider dynamics of quantum uncertainty relations of the quantum coherence and their lower bounds under the amplitude damping channel (ADC). We find that ADC changes the uncertainty relations and their lower bounds, and their tendencies depend on the initial state. In this paper, we only consider the influence under the amplitude damping channel, and other Markovian channels can be considered by the similar method.
This paper is organized as follows. We briefly recall some notions we are going to use in our analysis in Section
In this section, we review some notions related to quantifying the quantum coherence. Considering a finite-dimensional Hilbert space H with d = dim(H). Let {|i⟩, i = 1, 2, …, d} be a particular basis of H. A state is called an incoherent state if and only if its density operator is diagonal in this basis, and the set of all the incoherent states is usually denoted as Δ. Baumgratz et al.[27] have proposed that the quantum coherence can be measured by a function C that maps a state ρ to a non-negative real value, moreover, C must satisfy the following properties: C(ρ)≥ 0 and C(ρ) = 0 if and only if ρ ∈ Δ; C(ρ)≥ C(Φ(ρ)), where Φ is any incoherent completely positive and trace preserving map; C(ρ)≥ ∑ipiC(ρi), where 


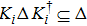
In accordance with the criterion, several coherence measures have been studied. It has been shown that l1 norm of coherence,[27] relative entropy of coherence,[27] the quantum coherence via skew information,[28] and geometric coherence[29] satisfy the above four conditions.
The relative entropy of coherence[27] is defined as
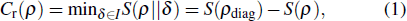 |
l1 norm of coherence[27] is defined as
 |
The quantum coherence via skew information[28] of ρ is defined as
 |
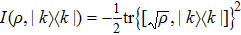
The geometric coherence is defined by Streltsov et al.[29] as follows:
 |
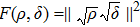
 |
In this section, we consider quantum uncertainty relations of the above four coherence measures for single-qubit states. Considering a single qubit state ρ with spectral decomposition
 |

 |


 |
For convenience, we first show the following lemma.
Given a single qubit state ρ, we can find a corresponding value ω. Therefore, for convenience, we replace θ + ω with θ in the following. Hence, we have |⟨x0|φ⟩|2 = sin2(θ), furthermore, |⟨x0|φ⊥⟩|2 = |⟨ x1|φ⟩|2 = cos2(θ), and |⟨x1|φ⊥⟩|2 = sin2 (θ). Similarly, we have |⟨y0|φ⟩|2 = |⟨y1|φ⊥⟩|2 = sin2(θ + ε), and |⟨y0|φ⊥⟩|2 = |⟨y1|φ⟩|2 = cos2(θ + ε).
After the projective measurements X and Y, the states of the system are given, respectively, by
 |
Based on the above preliminaries, we consider quantum uncertainty relations of the above quantum coherence measures. Instead of optimizing the uncertainty relations over all possible states ρ, we will optimize them over θ. We first present quantum uncertainty relations of REOC as follows.
Theorem
 |
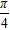
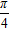

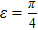
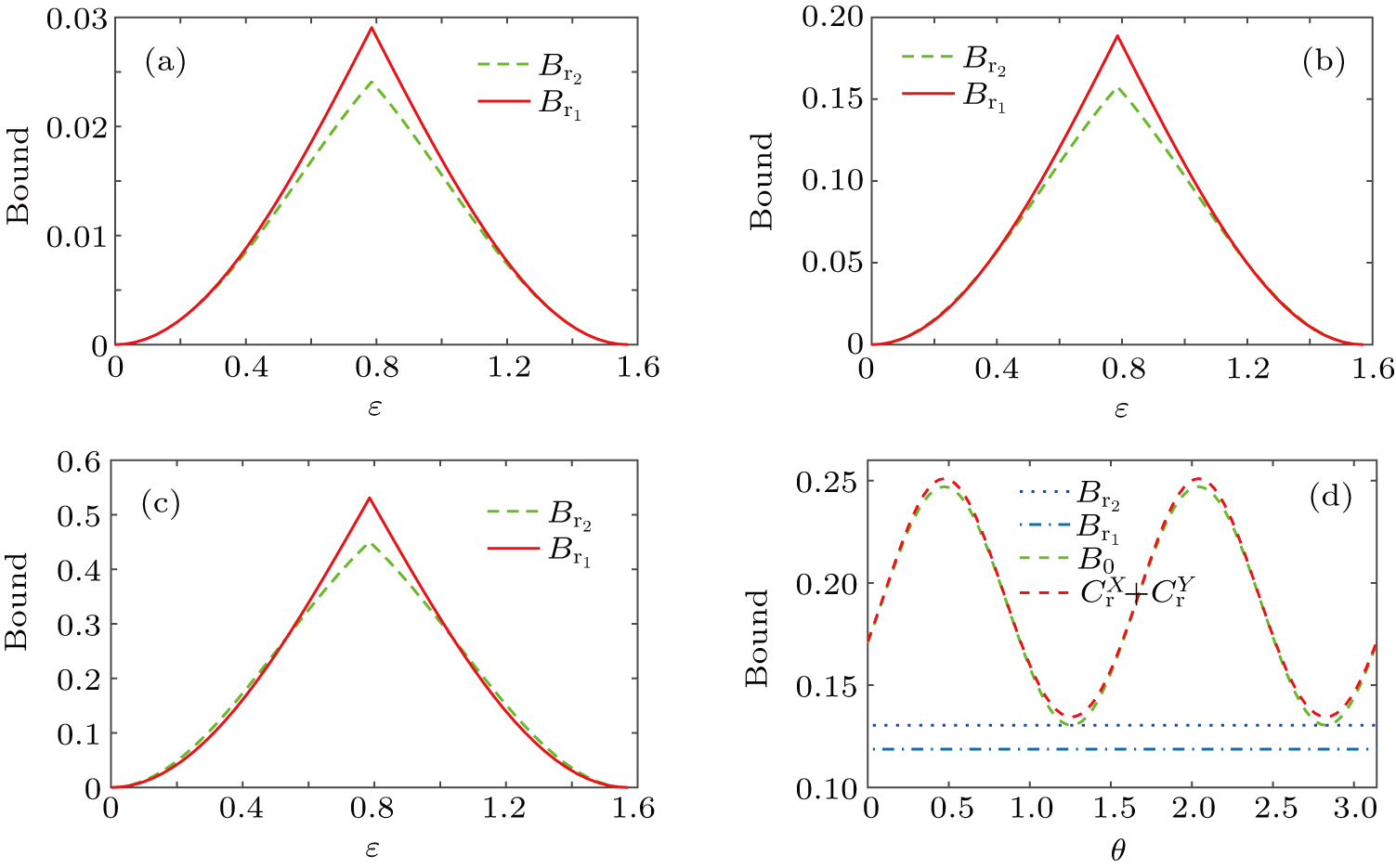 | Fig. 1. (color online) The comparison between Br1 and Br2 for the cases of (a) p = 0.65, (b) p = 0.8, and (c) p = 0.95; (d) Br1(θ), Br1, Br2, and   |
According to Eq. (
Now, we consider a quantum uncertainty relation of SIC based on bases X and Y, and give a lower bound of 

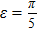
According to Eq. (
In Ref. [52], Yuan et al. have given a quantum uncertainty relation of l1-norm of coherence based on two fixed bases, and a lower bound of 

In the following, we will show f(α) = |sin(α)| + |sin(α + β)|≥ |sin(β)|, where 
According to Eq. (
Next, we consider a quantum uncertainty relation of GC based on bases X and Y, and give a lower bound of 
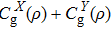
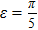
According to Eq. (
In this section, to answer the question (ii) in Section 

 |

 |





We first compare Br1, BSI, Bl1, and Bg with 



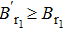






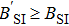





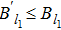

Next, we discuss the variation of 

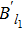
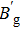






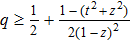

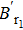
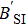

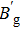
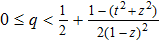
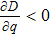




 | Fig. 3. (color online)  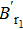 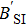 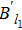  |
In the following, we investigate dynamics of LHSs of Eqs. (
We consider some special cases as follows:
(I) In the case of cos(2θ) ≥ 0, sin(2θ)≤ 0, cos(2θ + 2 ε)≥ 0, and sin(2θ + 2 ε) ≤ 0. That is to say 


 |
We denote 



(II) In the case of cos(2θ) < 0, sin(2θ) > 0, cos(2θ + 2 ε) < 0, and sin(2θ + 2 ε) > 0. That is to say 

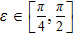
 |
Similar to case (I), when M ≥ 1, 


(III) In the case of cos(2θ)< 0, sin(2θ) > 0, cos(2θ + 2 ε) > 0, and sin(2θ + 2 ε) < 0. That is to say 
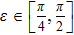
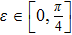
 |
We denote 





(A) Given a state ρ1 with parameters 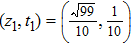
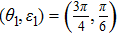
(B) Given a state ρ2 with parameters 

(C) Given a state ρ3 with parameters 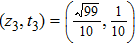
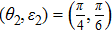
(D) Given a state ρ4 with parameters 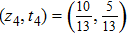

(E) Given a state ρ5 with parameters 

(F) Given a state ρ6 with parameters 

Now, we consider dynamic of the LHS of Eq. (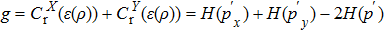

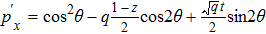

It is a difficult task to calculate LHSs of Eqs. (
In this paper, we discussed quantum uncertainty relations of quantum coherence through a different method from Ref. [52]. We obtained some lower bounds with parameters, and their minimal bounds. Moreover, we found that for two pairs of measurement bases which have the same maximum overlap, the different quantum uncertainty relations and lower bounds with parameters maybe obtained, but the same minimal bounds can be obtained. This result answered the question (i) posed in Section
There are many further issues that need to be solved in the future. We can discuss the uncertainty relations for other coherence measures. We only considered dynamics of of quantum uncertainty relations of quantum coherence under ADC. Dynamics of quantum uncertainty relations of quantum coherence under any incoherent operator[27] (strictly incoherent operation and maximally incoherent operation[45]) is an interesting subject. Quantum uncertainty relations based on many fixed bases are also an interesting subject for future work.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] |









