† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11474236, 81671674, and 11775184) and the Science and Technology Project of Fujian Province, China (Grant No. 2016Y0078).
An ill-posed inverse problem in quantitative susceptibility mapping (QSM) is usually solved using a regularization and optimization solver, which is time consuming considering the three-dimensional volume data. However, in clinical diagnosis, it is necessary to reconstruct a susceptibility map efficiently with an appropriate method. Here, a modified QSM reconstruction method called weighted total variation using split Bregman (WTVSB) is proposed. It reconstructs the susceptibility map with fast computational speed and effective artifact suppression by incorporating noise-suppressed data weighting with split Bregman iteration. The noise-suppressed data weighting is determined using the Laplacian of the calculated local field, which can prevent the noise and errors in field maps from spreading into the susceptibility inversion. The split Bregman iteration accelerates the solution of the L1-regularized reconstruction model by utilizing a preconditioned conjugate gradient solver. In an experiment, the proposed reconstruction method is compared with truncated k-space division (TKD), morphology enabled dipole inversion (MEDI), total variation using the split Bregman (TVSB) method for numerical simulation, phantom and in vivo human brain data evaluated by root mean square error and mean structure similarity. Experimental results demonstrate that our proposed method can achieve better balance between accuracy and efficiency of QSM reconstruction than conventional methods, and thus facilitating clinical applications of QSM.
Nuclear magnetic resonance (NMR) has now reached a remarkable degree of maturity and become a widely available technique in medical and biological applications.[1–3] Magnetic susceptibility serves as an intrinsic physical property of a substance that can provide tissue contrast mechanism in proton magnetic resonance imaging (MRI).[4,5] Quantitative susceptibility mapping (QSM) based on magnetic resonance phase images has become a promising technique for quantifying this property.[6] The QSM has the ability to accurately evaluate the strong susceptibility sources including deoxyhemoglobin and hemoglobin degradation products,[7] investigate iron deposition to differentiate neurodegenerative patients and healthy control,[8–10] and quantify changes of demyelination and iron levels during the formation of multiple sclerosis lesions.[11] As a result, it provides a valuable insight into the diagnosis of specific diseases, such as cerebral hemorrhage, neurological diseases, and multiple sclerosis.
Reconstruction of the susceptibility map is an ill-posed inversion problem due to the singularity around the magic angle of the dipole convolution kernel for the phase to susceptibility transformation.[12] Various strategies have been developed to solve this ill-conditioned problem. Calculation of susceptibility through multiple orientation sampling (COSMOS), which is referred to as the gold standard when compared with the QSM algorithms, may be impractical in clinical applications because of inconvenient data acquisition in different orientations.[13] In regard to single-orientation reconstruction methods, a fast and simple method is truncated k-space division (TKD),[14] which applies a threshold to the dipole kernel. Despite easy implementation, threshold selection is usually a trade-off between the level of streaking artifact and the under-estimation of susceptibility. Another choice of single-orientation methods is to introduce a penalty term and solve the regularization problem by using an optimization algorithm.[15–21] For example, morphology enabled dipole inversion (MEDI),[18,19] where the priori anatomical information from the magnitude map is utilized, has proved to be an effective method of reconstructing susceptibility.[22] However, the long reconstruction time is a major issue for MEDI and other similar regularization methods, which may restrict their clinical applications. The total variation using split Bregman (TVSB) proposed by Bilgic et al. accelerates the L1-regularized susceptibility reconstruction.[23,24] Nevertheless, this method abandons the data weighting matrix in the data fidelity term to employ split Bregman iteration, while data weighting has proved to be significant in artifact suppression,[25] especially around the region of strong susceptibility variation like blood vessels.
In this work, we propose a weighted total variation using split Bregman (WTVSB) to accelerate the L1-regularized susceptibility reconstruction. By combining split Bregman iteration with noise-suppressed data weighting, WTVSB realizes the balance between quality and efficiency in QSM reconstruction. The performance of WTVSB is compared with those of TKD, MEDI and TVSB using numerical simulation, gadolinium phantom, and in vivo human brain data evaluated in terms of root mean square error (RMSE) and mean structure similarity (MSSIM). The influence of parameters in noise-suppressed data weighting on the quality of susceptibility map is also measured. This work may promote the potential applications of QSM in clinical diagnosis and treatment.
The local magnetic field can be represented as the convolution of the dipole kernel with the susceptibility distribution, as well as multiplication between the susceptibility and dipole kernel in the Fourier domain, which can be generally written as
 |
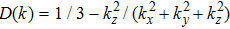
Regularization constitutes a common approach to process an ill-posed inverse problem. Regularized QSM methods often make use of the observation that the edges in the susceptibility maps are nearly the same as those in magnitude images obtained in the same subject, and their inconsistency can be considered to be sparse. To satisfy this sparsity, we apply a weighted L1 minimization that penalizes voxels on the susceptibility map, which are inconsistent with the magnitude image. Accordingly, the susceptibility reconstruction is formulated as a constrained minimization problem:
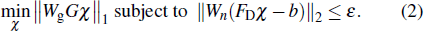 |
The solution of the constrained convex optimization problem in Eq. (
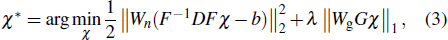 |
Many algorithms have been proposed to solve this optimization problem, such as a nonlinear conjugate gradient method,[16,21,23] and lagged diffusivity fixed point method.[17,26] The time-consuming process restricts these solvers’ clinical applications. Therefore, a valid solution with an accelerated process is expected.
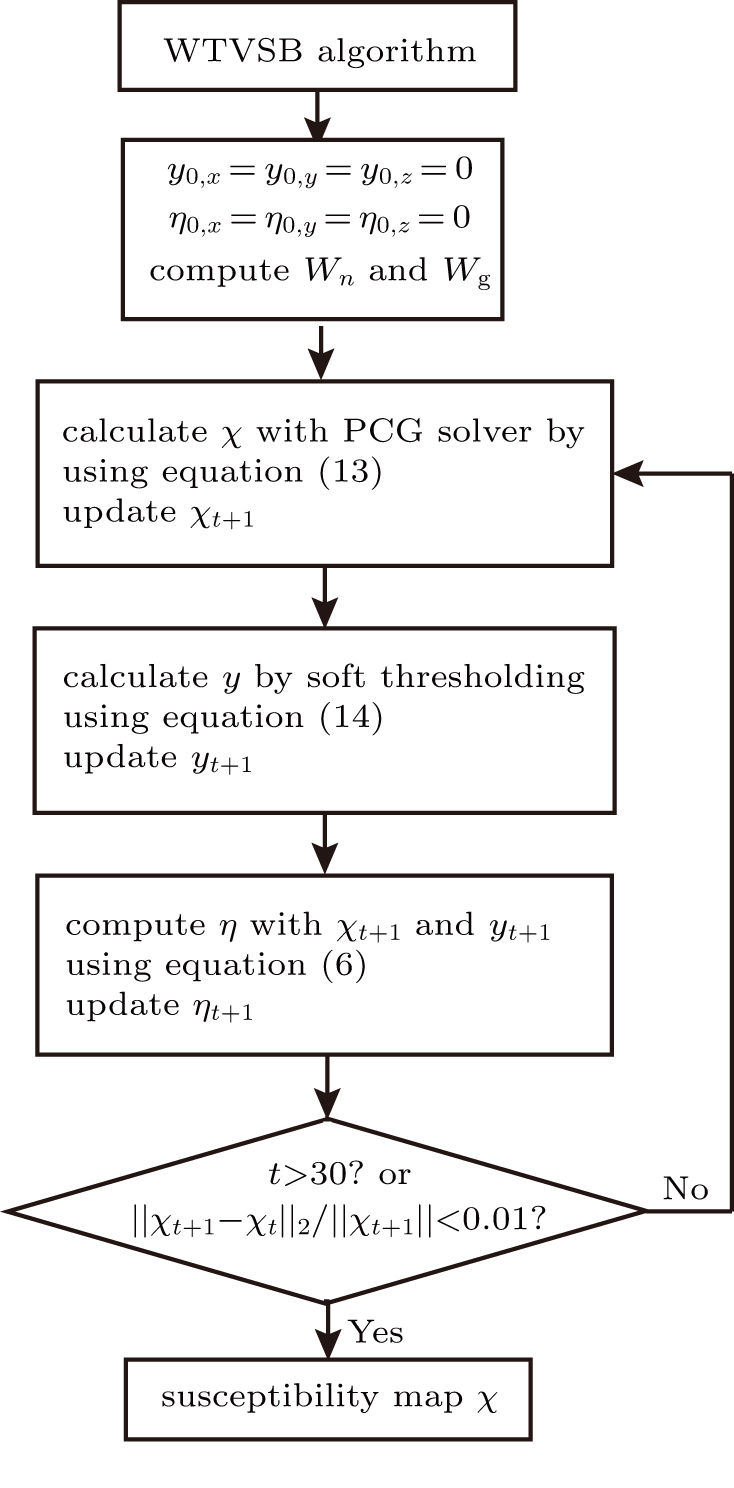
In this study, we propose a new reconstruction method which combines split Bregman iteration and noise-suppressed weighting in the data fidelity term. The split Bregman iteration is achieved by introducing an auxiliary variable y. The noise-suppressed data weighting matrix Wn is used to suppress the spread of noise and errors from calculated field to susceptibility map. The susceptibility reconstruction is formulated as
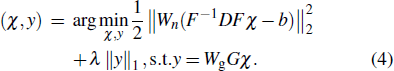 |
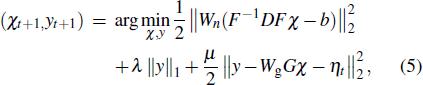 |
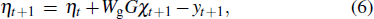 |
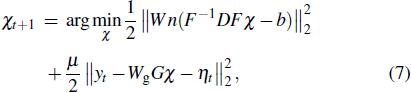 |
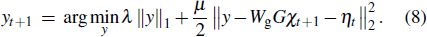 |
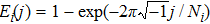
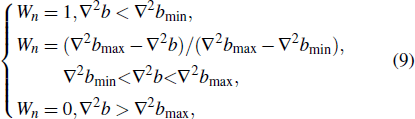 |
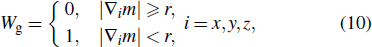 |
With simultaneously adding and subtracting a temporary term (I − Wn)F−1DFχ (I is a unit matrix with the same size as Wn), equation (
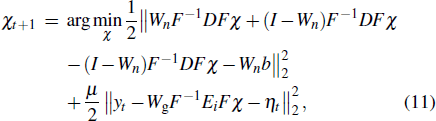 |
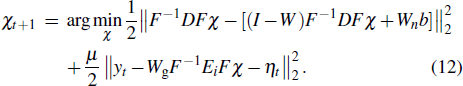 |
The optimal condition for Eq. (
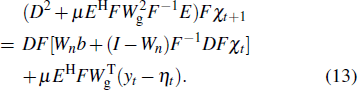 |
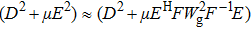
Equation (
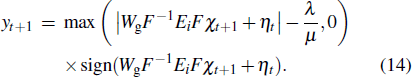 |
The performance of the WTVSB method was evaluated on a numerical model with pre-known susceptibility, gadolinium phantom, and in vivo data in comparison with TKD,[14] MEDI,[18,19] and TVSB.[23] The RMSE and MSSIM with respect to the references (known susceptibility of numerical model and COSMOS for gadolinium phantom and in vivo human brain data) were used for quantitative performance evaluation. The datasets of gadolinium phantom were downloaded from website (
A three-dimensional numerical brain model with a matrix size of 256 × 256 × 150 was created based on an actual susceptibility map followed by manual segmentation of different anatomical regions. The background area and cerebrospinal fluid regions were set to be zero susceptibility. In cerebral regions, the white matter region was set to be −0.05 ppm, cortical gray matter to 0.04 ppm, veins to 0.35 ppm, and the caudate nucleus, putamen, globus pallidus, red nucleus, substantia nigra, and dentate nucleus to 0.08, 0.1, 0.19, 0.14, 0.16, and 0.09 ppm, respectively. Normally distributed noise with a standard deviation of 3% susceptibility values was added to mimic random physiological susceptibility variations. The field perturbation of the model was generated by fast forward field computation. In addition, the GRE magnitude image was simulated according to the corresponding T1, 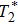
A phantom was utilized for experimental validation, the same as the one carried out by Wang et al.[5] Five spherical balloons were filled with gadolinium solutions of various concentrations, which were immersed in a cylindrical container filled with 2% agarose gel. The susceptibility values in five balloons were 0.8, 0.4, 0.2, 0.1, and 0.05 ppm respectively. This phantom was imaged on a 3 T scanner (HDx, GE healthcare, Waukesha, WI) with a multi-echo gradient echo sequence. The imaging parameters were as follows: repetition time (TR) = 70 ms, echo time (TE) = 5 ms ∼ 40 ms, echo spacing (ΔTE) = 5 ms, bandwidth = 480 Hz/pixel, and flip angle (FA) = 15°. The resolution was 1 mm×1 mm×1 mm with a matrix size of 130 × 130 × 86.
In vivo human data were acquired at the F M Kirby Research Center in the Kennedy Institute and Johns Hopkins University Hospital. Institutional review board (IRB) approval and written informed consent were obtained following a complete description of the study. A healthy volunteer was acquired on a 7 T Philips Healthcare MRI equipped with a 32-channel Novamedical head receive coil. A three-dimensional multi-echo gradient recalled echo (GRE) sequence was utilized. The scan parameters were set to be as follows: TR = 45 ms, TE1 = 2 ms, ΔTE = 2 ms, field of view (FOV) = 220 mm × 220 mm × 110 mm, matrix size = 224 × 224 × 110, the number of echoes = 9, flip angle = 9°, and SENSE factor = 2.5 × 2 for the phase encoding directions. Fat suppression was accomplished by using a water-selective ProSet 121 pulse. Data in multiple head orientations were acquired to calculate susceptibility maps with COSMOS,[13] which were used as references for the adjustment of the regularization parameters and standard values for comparing with the results from different single-orientation QSM reconstruction methods. The volunteer’s head was at four positions: normal supine position, titled to the subject’s right shoulder, titled to the subject’s left shoulder, and titled to the subject’s back. The rotation angle for each orientation varied randomly in a range from 5° to 22° with respect to the main B0 direction.
For the gadolinium phantom, the field was first estimated from the multi-echo datasets with a nonlinear fitting algorithm,[28] and then a magnitude image guided spatial phase unwrapping[29] was implemented to address the frequency aliasing on the field map. A method based on projection onto the dipole field was used to eliminate the background field.[30] For in vivo human brain data, phase wraps were removed by a Laplacian-based phase unwrapping method.[31] The frequency shift of each voxel was calculated by least squares fitting of the linear slope with the phase as a function of TEs using multiple echoes. The initial phase could be estimated by the linear fitting of the phase along with time and we utilized the initial phase to exclude some voxels which had unreliable phase measurement. To remove the background field mainly caused by the susceptibility variations around the air-tissue interfaces, a modified SHARP method (radius = 5 mm, regularization parameter = 0.06) was utilized.[32] Specifically, the radius of the spherical mean filter decreased as it approached to the brain boundary.[21] Different background removal methods were used to test whether or not WTVSB is suitable for inversion from the local field processed by different methods to the tissue susceptibility. We utilized the brain extraction tool (BET) in FMRIB Software Library (FSL, University of Oxford) (FSL BET) to generate the binary mask with the magnitude image. The mean normalized GRE magnitude image at the sixth echo was used to generate the weighting matrix, which performed appropriate tissue contrast at 7 T scanner. Serving as the gold standard susceptibility reference, COSMOS based susceptibility maps were calculated by using the LSQR algorithm with a relative convergence tolerance of 10−5.
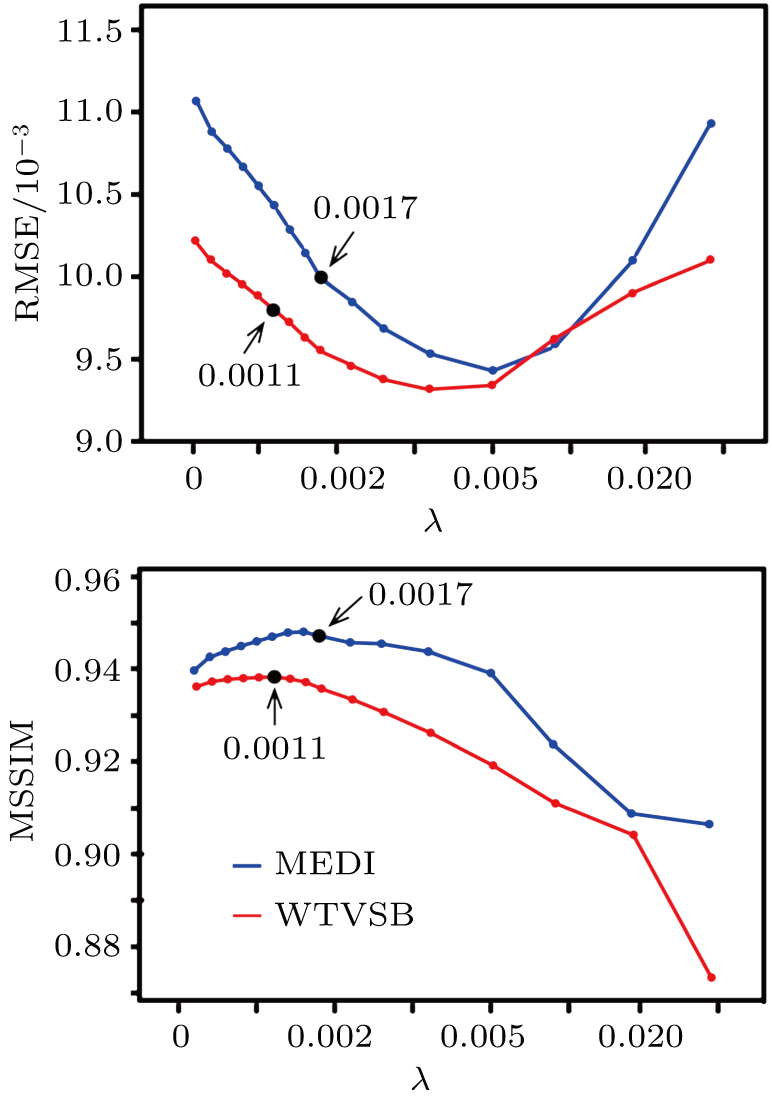
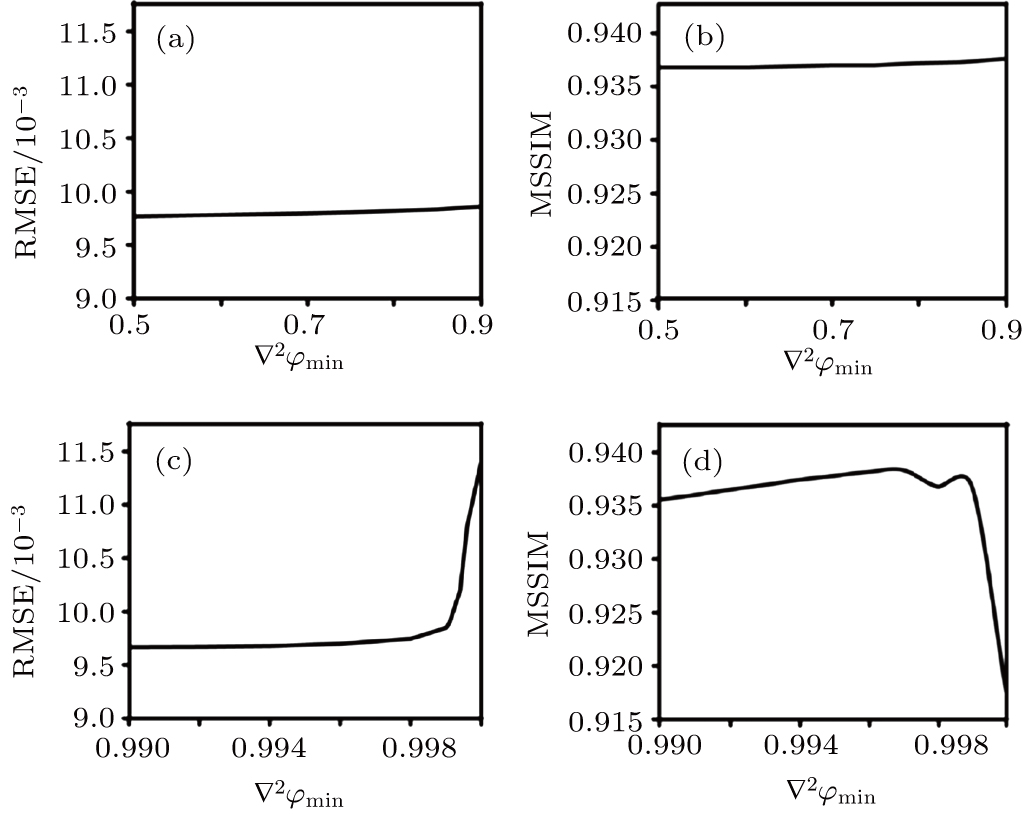
The optimal regularization parameters for MEDI and WTVSB were selected according to RMSEs and MSSIMs of the reconstructed susceptibility maps with different values relative to the numerical susceptibility model, and the corresponding COSMOS maps of the gadolinium phantom and human brain, respectively. Regularization parameter λ adjusts the weight of data fidelity. The decrease of λ leads to strong constraint on the data fidelity but streaking artifacts may not be suppressed effectively, and vice visa. So the choice of the values of regularization parameter λ in MEDI and WTVSB achieves a trade-off between data fidelity and streaking artifacts. Figure
The simulated local field map, the Laplacian of the local field, and the corresponding noise-suppressed data weighting are described with two typical slices in Fig.
 | Fig. 4. (color online) Simulated local field map, Laplacian of the local field, and corresponding noise-suppressed weighting in the numerical susceptibility model. |
In Fig.
| Table 1. Quantitative comparison of different methods in accuracy and reconstruction time. . |
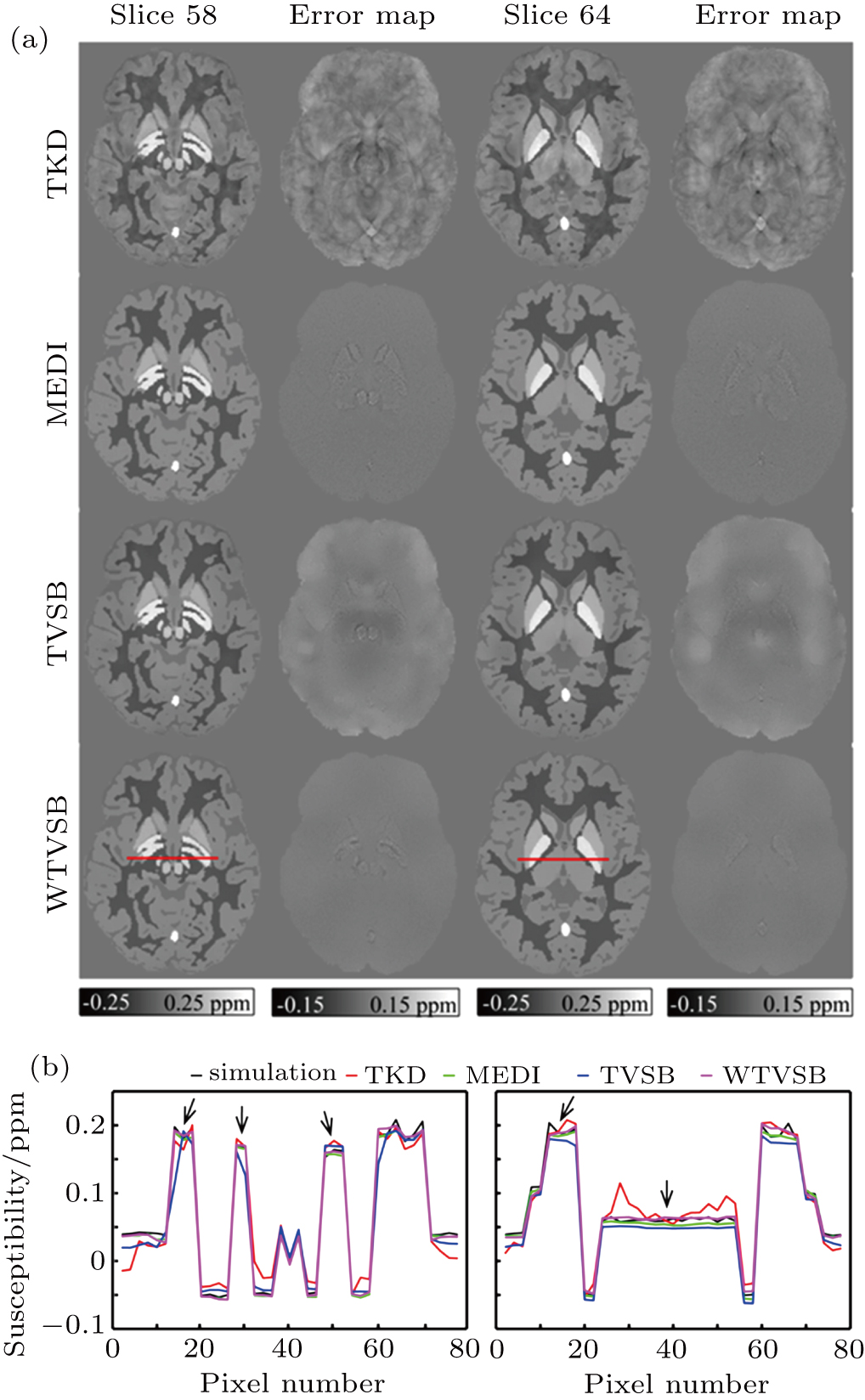
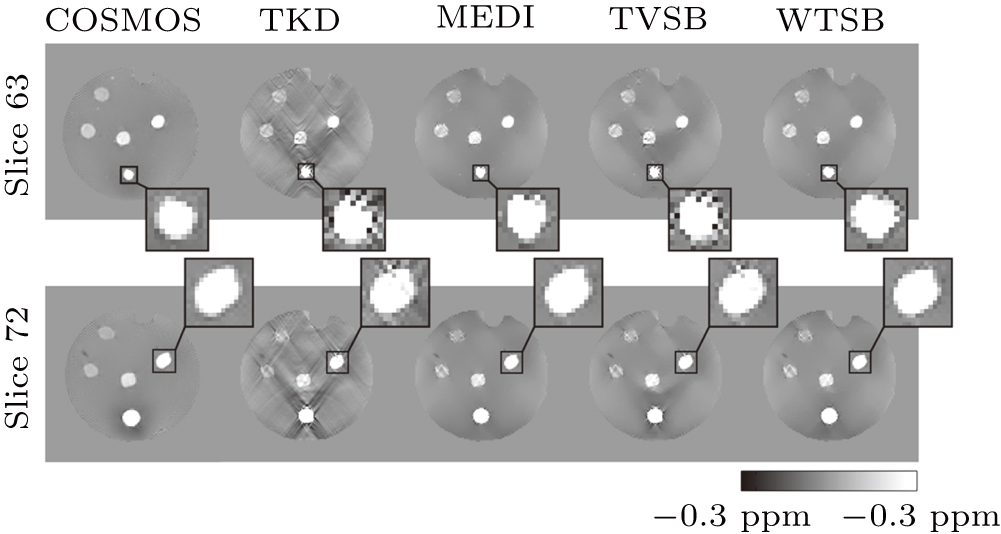
The reconstructed results from COSMOS, TKD, MEDI, TVSB, and WTVSB for the gadolinium phantom are shown in Fig.
Figure
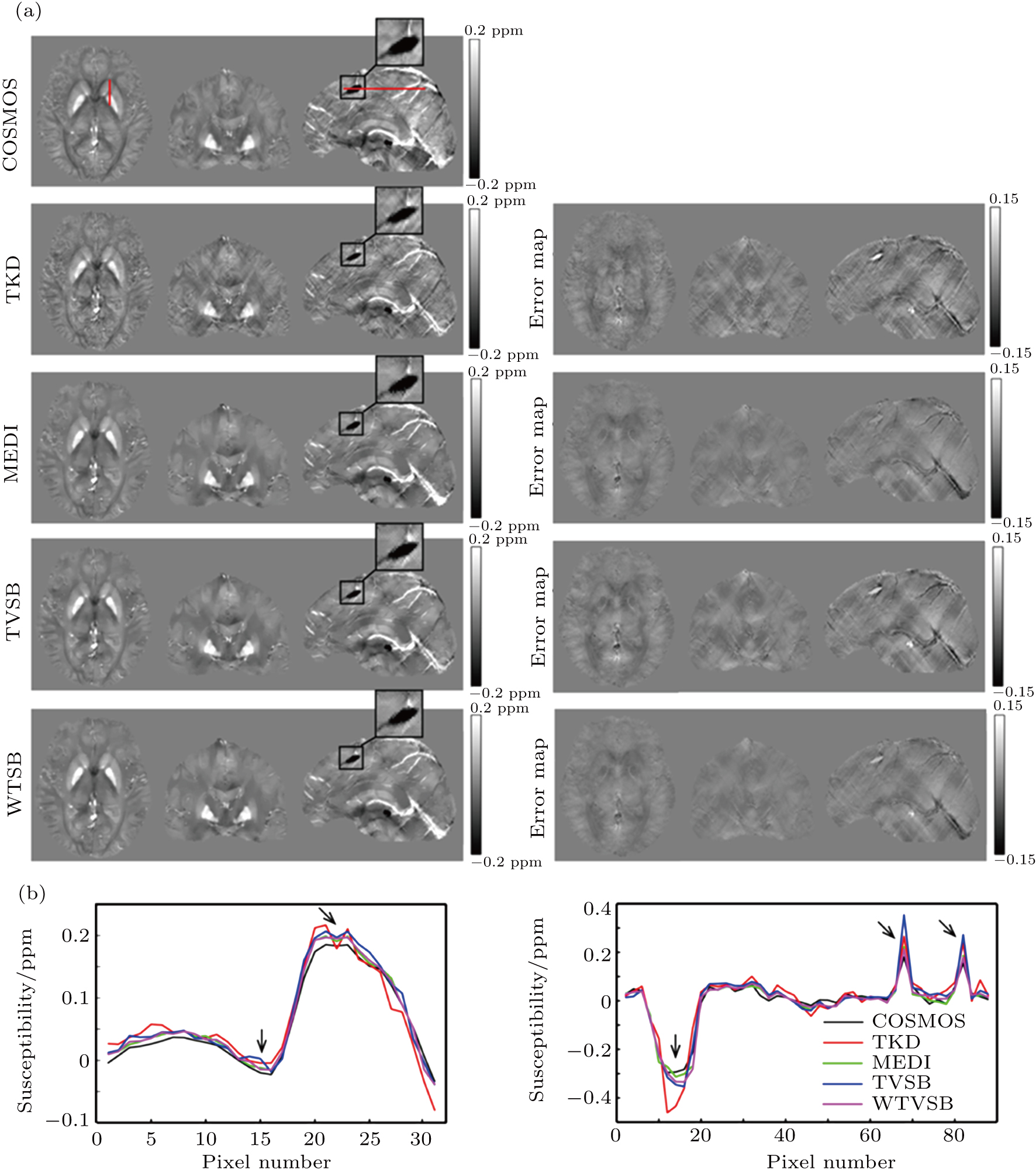
Figures
Quantitative comparisons of accuracy and reconstruction time among all methods are listed in Table
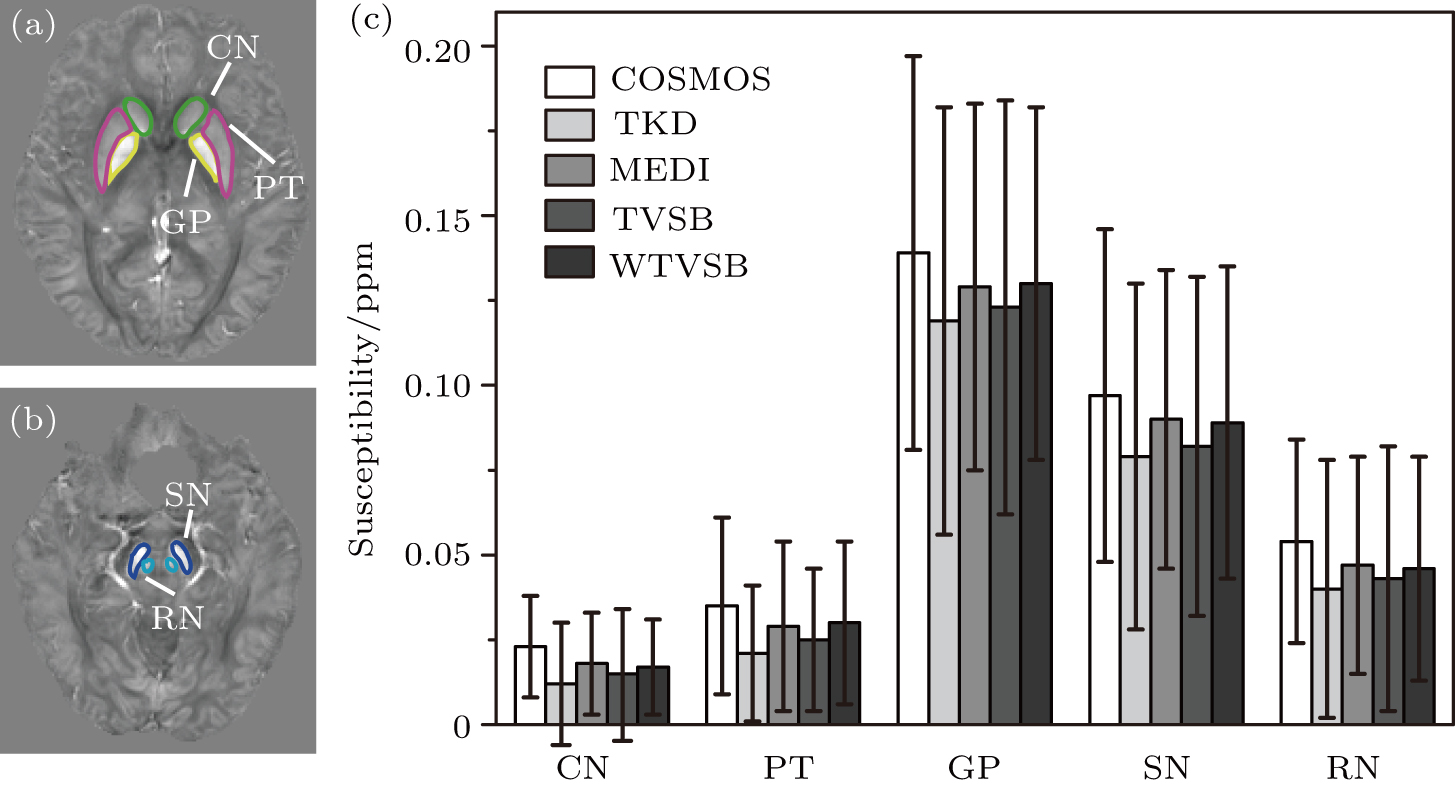
As shown in Fig.
In this study, an improved fast L1-regularized QSM reconstruction method is proposed to suppress the artifacts and minimize noise amplification in the susceptibility map. In this method, noise-suppressed data weighting is used to restrain the spread of errors from magnetic field to susceptibility and is appropriately combined with the split Bregman iterations, which results in the acceleration of susceptibility reconstruction. The qualitative and quantitative analyses indicate that the QSM map calculated from WTVSB is comparable to MEDI and superior to TVSB and TKD, and the reconstruction speed is much faster than those of MEDI and the conventional L1-regularization method.
Due to the structure property of the dipole kernel, the noise and errors in the field map will introduce severe streaking artifacts in the reconstructed susceptibility map. The data weighting is utilized to identify these bad points and suppresses the spread of noise and errors in the process of susceptibility inversion. Although a data weighting term exists in both MEDI and WTVSB methods, they play different roles in the implementation. On one hand, the structures of weighting matrix are different. The data weighting in MEDI serves as a normalized diagonal matrix whose diagonal elements are determined by the corresponding magnitudes. This weighting mask can be adjusted after each iteration to further reduce the weightings of bad points.[28] Whereas in the process of WTVSB reconstruction, based on the observation that the noise and errors in the field map usually exist in regions with sharp field changes, the weighting is determined by the Laplacian of the calculated local field. Most of diagonal elements in the resulting diagonal matrix are computed as 1 except for those positions with noisy field points. On the other hand, the weighting effects between them are distinct. Each diagonal element in the matrix of MEDI represents the reliability of corresponding field point, thus different field points would have different influences during the inversion of QSM. By contrast, the field points in the WTVSB method with low weighting are updated in each iteration to obtain a more accurate field. In other words, the effect of data weighting is converted into the update of field data. Anyway, these two weighting schemes both perform effective artifact suppression in the process of QSM reconstruction. A more concrete comparison is beyond the scope of this work.
Split Bergman iteration, which obviously accelerates L1-regularized reconstruction, has also been applied in MRI and CT image reconstructions.[33,34] In the original TVSB method, the introduction of preconditioner D2 + μE2 makes reconstruction quickly solved, because the valid approximation 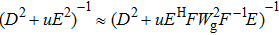
For TV regularized methods in QSM reconstruction, a precise gradient weighting helps to mitigate the over-smoothness of edges and improve the accuracy of susceptibility map.[22] In this study, like MEDI, the gradient weighting is determined by the magnitude based on the structural consistency between the magnitude and susceptibility. Phase information always serves as another choice for priori gradient in previous studies. A piece-wise gradient weighting from an initial susceptibility obtained by a fast QSM method[27] is also developed and proves to be effective. However, in the cases where noise and errors in field map are abrupt, the obtained initial susceptibility is usually polluted by streaking artifacts, which affect the final susceptibility value in the reconstruction. So it seems infeasible to obtain valid priori gradient using the fast-calculated initial susceptibility. Advanced image processing algorithms may be helpful to obtain a better priori gradient and further improve the quality of WTVSB reconstruction. Nevertheless, WTVSB is introduced to suppress the artifacts in QSM maps as well as to keep the time efficiency, so it may be improper to bring in more complicated processing.
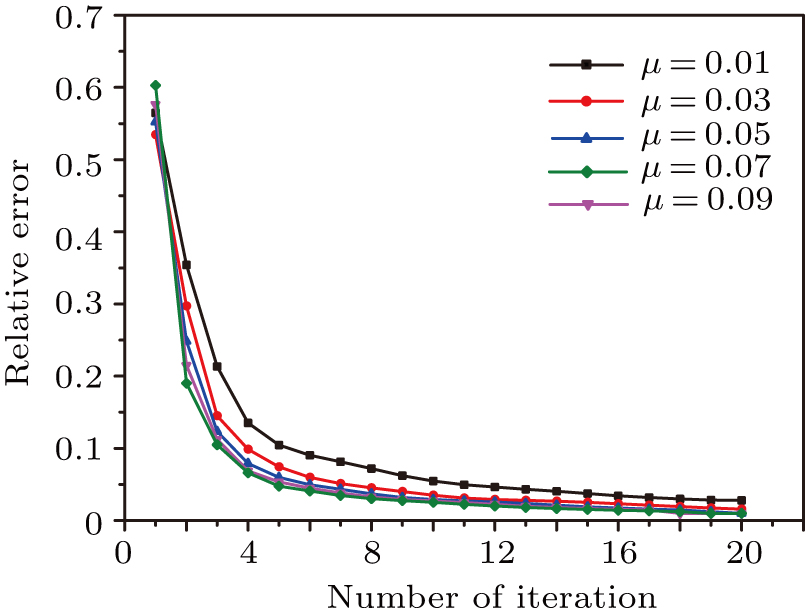
A fault for WTVSB is that it needs a pair of appropriate thresholds to adjust the contribution of data weighting. According to the in vivo human brain experiments detailed in Section
In this work, a noise-suppressed data weighting determined by the Laplacian of the calculated local field is proposed to help to restrain the spread of noise and errors in susceptibility inversion, which is suited to be incorporated with split Bregman iterations for the acceleration of L1-regularized susceptibility reconstruction. Through appropriate combination of data weighting and split Bregman iterations, the weighted total variation using split Bregman (WTVSB) QSM method effectively facilitates the suppression of streaking artifacts in susceptibility map and retain the efficiency of reconstruction. The balance between computational efficiency and reconstruction accuracy is reasonably realized, which may promote the clinical diagnostic applications of QSM.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |