† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61575040 and 61635005) and the 111 Project, China (Grant No. B14039).
Transverse localization of the optical Tamm plasmon (OTP) is studied in a metal-distributed Bragg reflector (DBR) structure with a one-dimensional disordered layer embedded at the interface between the metal and the DBR. The embedded disordered layer induces multiple scattering and interference of light, forming the light localization in the transverse direction. This together with the formation of Tamm plasmonic modes at the metal-DBR interface (i.e., the confinement of light in the longitudinal direction), gives birth to the so called transverse-localized Tamm plasmon. It is shown that for both transverse electric (TE) and transverse magnetic (TM) polarized light injection, the excited transverse-localized Tamm plasmon broadens and splits the dispersion curve due to spatial incoherence in the transverse direction, thus proving the stronger light confinement especially in the TE polarized injection. By adding the gain medium, specific random lasing modes are observed. The proposed study could be an efficient way of trapping and locally enhancing light on a subwavelength scale, which is useful in applications of random lasers, optical sensing, and imaging.
Light localization has been extensively investigated in recent years since its potential applications in many fields, such as photonic integrations, optical manipulation, optical sensing, novel light source designing, light harvesting, etc.[1–9] It is known that light localization in a structured optical medium resembles that of electrons in solids,[1,3] causing the propagation of photons to be completely suppressed on account of the interference effect of multiple scattering waves in the scattering medium.[7–9] Usually, light localization can be obtained in many optical structures, such as microcavities, photonic crystals with defects, surface plasmon devices, and disordered nanostructures.[4–6] A relatively hot research branch of the light localization is the transverse localization, proposed first by Raedt et al. in 1989.[8] In 2007, Schwartz et al. observed the transverse localization experimentally for the first time by using two-dimensional (2D) photonic crystals.[2] Since then, the observation of the transverse localization has been reported sequentially in optical fiber,[7] disordered optical waveguide,[10] triangular optical lattices,[11] and so on.
Optical Tamm plasmon (OTP) is defined as a confined optical mode localized at the crystal surface, which was proposed at the beginning of the 21st century and opened up an attractive research subject.[12] The OTP can confine light at interface between two different DBRs or interface between a metal film and a DBR.[13–17] Compared with normal surface plasmon, OTP can be excited by both transverse electric (TE) and transverse magnetic (TM) polarized light with a much narrower resonance peak,[14–17] and it provides comparable or even stronger field enhancement. In addition, the OTP can find various applications, such as in high-performance low-cost hot-electron photodetection,[18] wavelength selective thermal emitters,[19] compact lasers, bistable switch, photovoltaic devices, filters, and optical sensors.[20–30] However, the confinement of OTP in the direction parallel to the interface between the metal and the DBR, i.e., the so-called transverse localization of OTP, is less studied currently.
Here, an OTP structure is presented by introducing a disordered layer at the interface of a metal-DBR structure, and transverse light localization at the interface (i.e., transverse localized Tamm plasmon) is demonstrated theoretically. Due to scattering of the disordered layer, several localized modes could be formed, showing spatially incoherent characteristics in the transverse direction. On the other hand, field distribution of the localized modes is also well confined in the longitudinal direction through the formation of OTP, providing considerably stronger intensity enhancement than the scenario of regular OTP. Besides, eigen wavelengths of the localized modes are also tailored by the dispersion relation of Tamm plasmon, thus broadening the bandwidth and inducing partially-random resonances. The proposed way of forming transverse OTP provides a novel way to trap light and form a spatially dependent mode of light-matter interaction, which is significant for realizing the optical control devices and random lasers in applications of imaging, sensing, and light harvesting.
Schematic diagram of the proposed structure is given in Fig.
First, we consider the case where there is no disordered layer in the top dielectric layer (case 1). The reflection spectrum of the homogeneous Tamm plasmon is given in Fig.
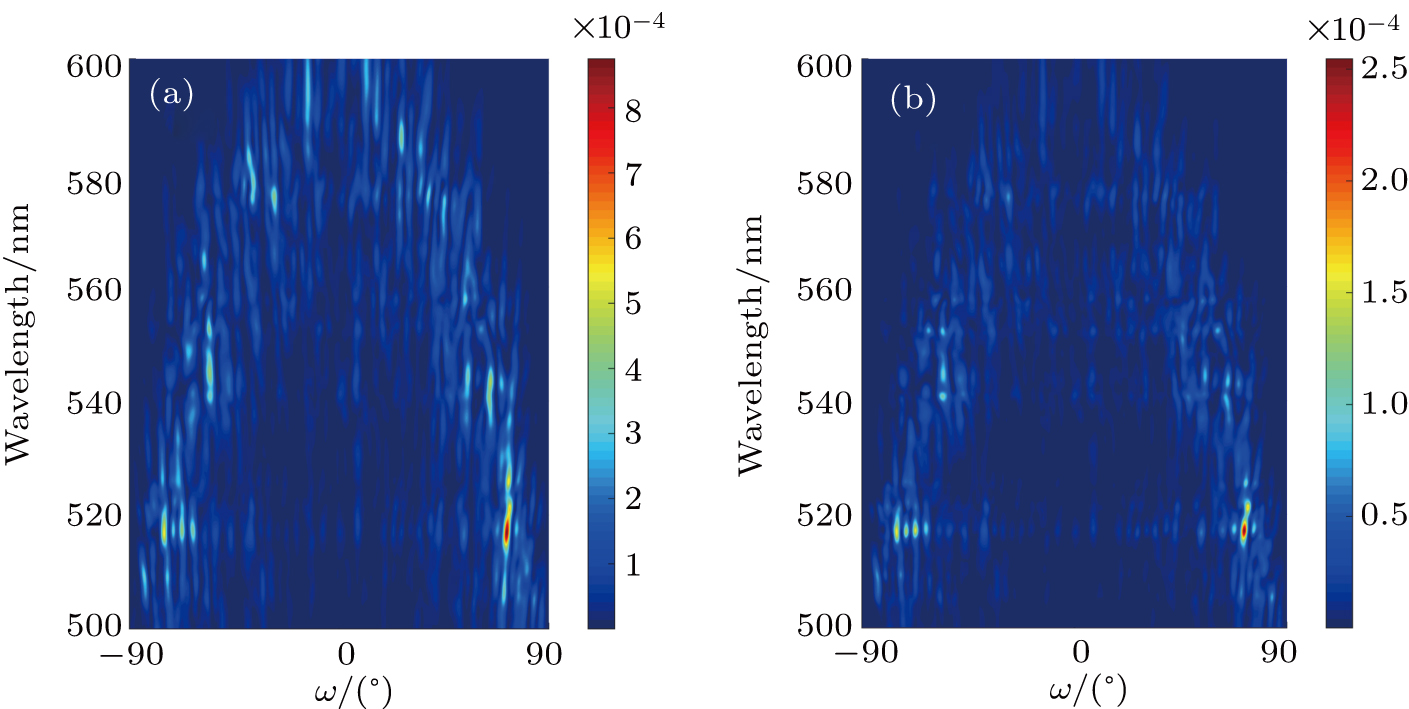
Dispersion characteristics of the transverse-localized OTP are discussed through reflection spectra of different injection angles as given by Fig.
Figure
To observe the photon localization phenomenon, electric field distributions in the neighborhood of dip wavelength for cases 1, 2, and 3 are given in Figs.
The plots of normalized electric field distribution |E/E0| (where E is the electric field intensity and E0 is the electric field intensity of the incident light) versus the transverse location and the injection wavelength for a fixed value of z (z = 62.738 nm) are shown in Fig.
Besides using the proposed structure (case 3), we also calculate the wavelength shift of the reflection dip at 594 nm when increasing the refractive index of the air gap. The sensitivity (the minimum detection limit of this sensing structure) is found to be ∼ 100 nm per refractive index unit, which is better than the reported result in Ref. [35] in which an OTP structure is used without random layers.
Strong scattering and amplification are necessary conditions for random lasing. In the successive study, the air gap in the random layer is replaced by a gain medium, which is the amplification mechanism introduced into case 3. To simulate this, dipoles’ sources are used in the center of each gain medium to mimic spontaneous light emission, and the gain medium is defined by the well-known Lorentz model with a central wavelength of 550 nm and bandwidth of 64.2 nm.[36] Figure
Finally, far-field intensity patterns with and without consideration of gain in the random layer of case 3 are given in Fig.
In this work, we propose a scheme to realize strong confinement of light in a Tamm plasmonic structure embedded in a disordered layer. Through the combined effect of light confinement at the metal-DBR interface and random light scattering and interference in the disordered layer, the transverse localization of Tamm plasmon is obtained. The new formed Tamm plasmon shows stronger light confinement with an inhomogeneous distribution of eigen modes as well as broadened and split dispersion curves. When gain is introduced into the structure, a random laser can be emitted, showing a partially random emission pattern that is tailored by the dispersion relationship of the TP. The proposed device could be useful for light trapping and enhancement in applications of random lasers, optical sensing, and imaging. The unique advantage of this work in sensing applications is that the transverse localization of OTP has a sharper dip as well as a larger quality factor than that of surface plasma (SP), and different localization modes correspond to different dips, which can be used to realize position-dependent sensing.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |