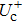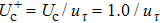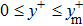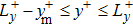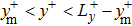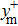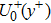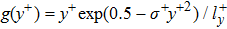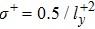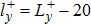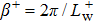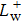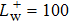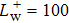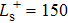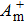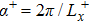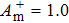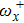A new kind of hairpin-like vortical structure induced by cross-interaction of sinuous streaks in turbulent channel
1. IntroductionThe hairpin vortex, also known as the horseshoe vortex, is a vortical structure model which is constituted by a Λ-like or Ω-like head that connects two counter-rotating legs underneath. Since the original proposal by Theodorsen[1] from the vorticity-transport form of the Navier–Stokes equations, it has been widely accepted that the hairpin vortical structures extensively exist both in the transitional and turbulent boundary layers.[2–6] Such a vortical structure is not only viewed as a typical behavior of the late stage of wall-bounded transitional flow, but also sheds some light on the characteristics of the fully developed turbulence, including the formation of the streaks, bursting events, and self-sustaining behavior.
In a regular wall-bounded transitional flow, the hairpin vortex is derived from the non-linear evolution of a Tollmien–Schlichting (T–S) wave, which has been studied extensively both numerically and experimentally.[7–9] According to the spatial arrangement of the Λ-like vortices, there are two kinds of transitional types named ‘Klebanoff-type (K-type)’,[7] and ‘Herbert-type (H-type)’;[8] the hairpins in the former type are aligned in rows while in the latter one they are interlaced. In the fully developed turbulence, the hairpin vortices often appear in groups (hairpin packets) in which a sequence of newborn hairpins can be generated by the primary hairpin vortex (PHV) — a phenomenon called ‘auto-generation’. Smith et al.[10,11] pointed out that the pressure force plays an important role in the formation of a secondary hairpin vortex (SHV). The new hairpin vortex is formed at the curve, either at the end of a leg or under the head of the PHV. Zhou et al.[12] followed the continuous generation of the hairpin vortices by direct numerical simulation (DNS) and addressed in detail the mechanism responsible for the auto-generation of hairpin vortices. They found that the SHV is the result of the self-induced motion of the PHV. The auto-generation of the hairpin vortex was also noted by Liu and Chen[13] who pointed out that the newborn hairpins are caused by the interaction between the primary streamwise vortices and the induced secondary streamwise vortices underneath. Another viewpoint of the hairpin formation is related to the instability of the varicose low-speed streaks, which was firstly examined by Asai et al.[14] in a flat-plate experiment. They considered that the instability of the varicose mode occurs due to the inflectional velocity profile across the streak in the normal-to-wall direction, which can result in the formation of hairpin vortices with a pair of counter-rotating streamwise vortices. Their experiment was further proved numerically by Brandt.[15]
The newborn hairpin vortices can also be induced by the collision of the adjacent coherent structures (CSs), including the vortices collision and streaks collision. Adrian et al.[16] speculated that new hairpins could be formed by the collision between spanwise adjacent hairpins when the spanwise size of hairpins grows, and their shapes depend on the shapes of the primary hairpins and their relative positions at the time of the encounter. Brandt and De Lange[17] numerically examined the interaction between streamwise-subsequent high- and low-speed streaks. Their numerical results showed that the symmetric collision of the head of the incoming high-speed streak with the tail of the low-speed streak could lead to the three-dimensional shearing that contributes to the breakdown of streaks and the formation of hairpin vortices. Konishi and Asai[18] studied the two spanwise adjacent low-speed streaks with subharmonic sinuous (SS) mode in the flat-plate experiment. They found that the unstable SS low-speed streaks can induce a pair of symmetric quasi-streamwise vortices which are then connected at their head and thus forming the hairpin vortex. Their experiment was further proved in our recent DNS results,[19] which pointed out that the collision between two spanwise adjacent low-speed streaks plays a key role in the forming of the hairpin vortices.
In a wallbounded channel flow, the CS derived from the opposite half of the channel can be interacted with each other near the center of the channel, which was called ‘cross-interaction’ by Sandham and Kleiser.[20] Earlier, Jiménez and Moin[21] by using DNS observed that the turbulence could be maintained on only one wall when reducing the size of the channel width to a 100-wall unit. They also addressed that the state of ‘one-side turbulence (OT)’ could not be kept for a long time and the turbulent state could be shifted from one wall to the other. Adrian and Liu[22] observed the evolution of the hairpin packets in the fully developed channel flow by using DNS and found that the hairpins derived from both halves could be collided in the normal direction near the center of the channel. However, they also noted that the normal collision of the hairpins is too complex to be examined due to the strong non-linear effects of the multiple vortices. Recently, Zhao et al.[23] developed a Lagrangian-based method to track the evolution of the vortex surface, and found that the vortex reconnection could occur when the near-wall hairpins collide with each other near the center of the channel. Their numerical results also showed that the vortex reconnection could lead to the sudden surge of wall skin frictions.
Turbulence is a complicated system in which many different scales of the flow structures interact with each other. The critical obstacle for the investigations on the channel cross-interaction is the chaos shape and spatial distribution of the CS. A better strategy is to simplify the complicated flow to an ideal collection of independent parts. In the present study, we will pre-set two sinuous low-speed streaks in a small size channel, one is located near the bottom wall while the other near the upper wall but with a similar pattern to the bottom one. By using DNS, we find that a new kind of hairpin-like vortical structure, named ‘normal-distributed hairpin-like vortex (NHV)’, can be induced by the cross-interaction between the upper and bottom streaks. The influence of the NHV on the turbulent statistical regularity is also revealed.
2. Numerical method and initial flow fieldFor the incompressible flow in the channel, the solutions are obtained by solving the momentum conservation and continuity equations:
where
u is the velocity vector,
p is the pressure, and
ν is the kinematic viscosity,
ν = 1/
Re. The simulation is performed at a low Reynolds number
Re = 1300 (corresponding to
Reτ = 80) based on the centerline velocity. The DNS based on the standard Fourier–Chebyshev spectral method
[24] is adopted to integrate Eqs. (
1) and (
2). The periodic condition and the Fourier expansion are adopted in the streamwise (
x) and the spanwise (
z) directions. In the wall-normal direction (
y), the Chebyshev polynomials are adopted for spatial discretization and the no-slip condition is imposed on both upper and bottom walls. A Chebyshev-
τ influence-matrix method is employed for the viscous (linear) term and the pressure term to ensure that the computed solutions satisfy both the incompressibility constraint and the momentum equation. Aliasing errors in
x and
z are removed by the 3/2-rule. As for time advancement, a semi-implicit back-differentiation formula (SBDF) with third-order accuracy is carried out for updating the nonlinear terms of the equation in time marching. Further details of the numerical methods and its applications can be found in our previous study.
[19,25–27]A sketch of the initial low-speed streaks in the computational box is shown in Fig. 1. The computational domain of the channel box just covers two low-speed streaks located on the opposite half of the channel, and the two streaks are symmetric with respect to the center of the channel. The baseflow velocity profile used in our study is taken from that described by Schappa and Hussain[28] but with some modifications. In order to perform a symmetric flow with respect to the center of the channel, the initial baseflow velocity distribution in the wall unit, U + (y+), is expressed as follows:
where
δ is the viscous length unit,
δ =
ν/
uτ,
uτ is the friction velocity, and its value is chosen so that it is in accordance with Dean’s empirical correlation,
[29]

(
Q is the constant-volume-flow rate per unit
z);
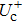
is the maximum mean velocity at the centerline of the channel,
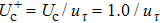
, and the superscript ‘+’ denotes the wall unit unless otherwise stated. In Eq. (
3),
Uturb values within
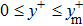
and within
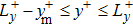
represent the turbulent mean profile, whereas
Ulam values within
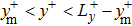
represent the laminar mean profile. To make sure that the curve of the baseflow velocity is continuous at
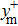
between the laminar and turbulent mean profiles,

values are set to be 0.92
h/
δ and 1.08
h/
δ (
h is the half height of the channel,
h = 1), respectively. Figure
2 shows the baseflow velocity profile
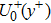
expressed by Eq. (
3). The baseflow velocity profiles of the near-wall turbulence are located on the upper half and bottom half of the channel, and they are symmetric with respect to the center of the channel.
The streamwise velocity distribution of the unfrozen streaks u+(y+, z+), which is taken as an initial condition, is expressed as follows:
Here, Δ
u+ is the streak velocity defect and Δ
u+ = 11.2;
g(
y+) is the normalized function, and its expression is
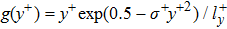
with
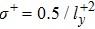
. To establish the symmetric streaks near the upper and bottom walls, we select

and
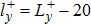
, which can make sure that the turbulent active region is consistent with the observed lifted streaks.
[28] β+ is the spanwise wave number and its value is
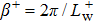
with
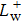
being the spanwise width of the streak and
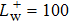
. Note that the streak width we choose corresponds to the averaged streak spacing observed in the turbulent boundary layer.
[21,28,30,31] Generally, the streak spacing and streak width are the same value collected from turbulent statistics, but they are two different physical concepts. The streak width is defined by the region where the low-speed streak lifted, and the streak lifted angle is closely related to the instability of the streak.
[28] While the streak spacing is the distance from the crown of one low-speed streak to that of the other adjacent one, it determines the spanwise evolution of the CS including the interaction between the adjacent streaks or between the vortices induced by the unstable streaks. Our previous work
[32] has shown that the turbulence could not be maintained for a long time but marches by setting two fundamental sinuous streaks in a channel when the streak spacing is equal to

, probably due to the constraint of the spanwise motion of the vortices. Therefore, to make sure that not only the streak lifted angle is identical to the observed streak in near-wall turbulence,
[28] but enough spanwise space is for the vortex evolution so that the turbulence can be sustained. Therefore,
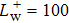
and
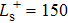
are chosen in the present study. The schematic diagram of the streak profiles is shown in Fig.
3.
For the size of the channel, the streamwise size (
 ) is taken as
) is taken as
 , which can match the streamwise length scale of a typical streamwise vortex.[33] The spanwise size (
, which can match the streamwise length scale of a typical streamwise vortex.[33] The spanwise size (
 ) is identical to the streak spacing, i.e.,
) is identical to the streak spacing, i.e.,
 . The channel height in the wall unit,
. The channel height in the wall unit,
 , is based on the viscous length unit,
, is based on the viscous length unit,
 . The computational grid points in the present study are 64 × 129 × 32 in the x, y, and z directions. The grid sizes Δx+ = Δz+ = 4.7, Δy+ = 0.024 (at the wall)-1.95 (in the center of the channel) are comparable to those used by Kim et al.[34] and Jiménez and Moin[21] with larger Reynolds numbers and were shown to be sufficient to resolve the essential turbulent scales.
. The computational grid points in the present study are 64 × 129 × 32 in the x, y, and z directions. The grid sizes Δx+ = Δz+ = 4.7, Δy+ = 0.024 (at the wall)-1.95 (in the center of the channel) are comparable to those used by Kim et al.[34] and Jiménez and Moin[21] with larger Reynolds numbers and were shown to be sufficient to resolve the essential turbulent scales.
To form the sinuous pattern of the low-speed streaks, the initial spanwise perturbation in the following form[28] is imposed on each straight streak:
where
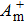
is the perturbation amplitude,
α+ is the streamwise wave number of perturbation, and
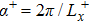
. The perturbation profiles expressed by Eq. (
5) are also drawn in colors on the iso-surface of the low-speed streaks in Fig.
1. When the opposite-signed spanwise perturbation starts to affect the flanks of the streaks, the initial straight streaks near the upper and bottom walls are simultaneously developed in sinuous mode with the same phase in the streamwise direction. In the following part, we will refer to such a symmetric flow pattern triggered by Eq. (
3)–Eq. (
5) as ‘symmetric doublesided turbulence (SDT)’.
3. Statistical propertiesThe effects of the initial spanwise perturbation amplitudes on the wall skin friction in the case of SDT are examined. Three initial perturbation amplitudes (
 , 0.5, and 1.0) are taken into account as shown in Fig. 4. When the initial spanwise perturbation amplitudes are above a certain threshold (
, 0.5, and 1.0) are taken into account as shown in Fig. 4. When the initial spanwise perturbation amplitudes are above a certain threshold (
 ), stochastic and intermittent behavior of the wall skin frictions are clearly visible, which can reflect the self-sustaining state of turbulence. For the streaks imposed by the critical initial perturbation amplitude (
), stochastic and intermittent behavior of the wall skin frictions are clearly visible, which can reflect the self-sustaining state of turbulence. For the streaks imposed by the critical initial perturbation amplitude (
 ), after a short period of decay, the wall skin friction quickly increases to the first peak value at t+ = 305 and then reaches to the self-sustaining state. While for the streaks imposed by the larger initial perturbation amplitude (
), after a short period of decay, the wall skin friction quickly increases to the first peak value at t+ = 305 and then reaches to the self-sustaining state. While for the streaks imposed by the larger initial perturbation amplitude (
 ), the initial decay of the wall skin friction is barely visible (reaches the first peak value at t+ = 179) and the self-sustaining behavior is rapidly reached. Since the initial condition in the channel only contains the lifted low-speed streaks without any initial vortices, the viscous diffusion dominates the near-wall flow in the initial stage and the streaks decay rapidly. When the initial disturbance amplitude is sufficient for significant nonlinear effects to be triggered, the streamwise vortex forms and its strength is enhanced rapidly. With enhancing the strength of the streamwise vortex, the streaks start to lift and oscillate, resulting in the rising of wall skin friction. For this reason, the initial decay of the wall skin friction is relatively short as the initial spanwise perturbation amplitude increases.
), the initial decay of the wall skin friction is barely visible (reaches the first peak value at t+ = 179) and the self-sustaining behavior is rapidly reached. Since the initial condition in the channel only contains the lifted low-speed streaks without any initial vortices, the viscous diffusion dominates the near-wall flow in the initial stage and the streaks decay rapidly. When the initial disturbance amplitude is sufficient for significant nonlinear effects to be triggered, the streamwise vortex forms and its strength is enhanced rapidly. With enhancing the strength of the streamwise vortex, the streaks start to lift and oscillate, resulting in the rising of wall skin friction. For this reason, the initial decay of the wall skin friction is relatively short as the initial spanwise perturbation amplitude increases.
Figure 5 shows the time histories of the upper and bottom wall skin frictions in the case of
 and
and
 . It can be seen that the upper and the bottom wall skin frictions are no longer coincident with each other after a certain time (t+ = 2900 for
. It can be seen that the upper and the bottom wall skin frictions are no longer coincident with each other after a certain time (t+ = 2900 for
 and t+ = 2480 for
and t+ = 2480 for
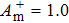 ), indicating that the flowfields in the upper half and bottom half are no longer symmetric with respect to the center of the channel. Such a phenomenon is unavoidable in a spectral method. Once a symmetric pattern is used as an initial condition, it takes a very long time for the machine epsilon to start to affect the flow. For this reason, the initial flow with a symmetric pattern cannot be kept marching for a long time. In this paper, however, we just focus on the evolution and statistics of the symmetric flow pattern. Since the symmetric patterns of the flowfields in the case of
), indicating that the flowfields in the upper half and bottom half are no longer symmetric with respect to the center of the channel. Such a phenomenon is unavoidable in a spectral method. Once a symmetric pattern is used as an initial condition, it takes a very long time for the machine epsilon to start to affect the flow. For this reason, the initial flow with a symmetric pattern cannot be kept marching for a long time. In this paper, however, we just focus on the evolution and statistics of the symmetric flow pattern. Since the symmetric patterns of the flowfields in the case of
 and
and
 are all kept before t+ = 2480, the statistics after t+ = 2480 is abandoned. Besides, because of the initial condition without any vortices, it needs enough time for the initial flow to reach a fully developed state, and the statistical status should be started at least after the wall skin friction has reached the first peak. For the above reasons, the statistical period we choose in the following ranges from t+ = 50 to 2480. In this statistical period, turbulence is fully developed and the flow pattern is symmetric with respect to the center of the channel.
are all kept before t+ = 2480, the statistics after t+ = 2480 is abandoned. Besides, because of the initial condition without any vortices, it needs enough time for the initial flow to reach a fully developed state, and the statistical status should be started at least after the wall skin friction has reached the first peak. For the above reasons, the statistical period we choose in the following ranges from t+ = 50 to 2480. In this statistical period, turbulence is fully developed and the flow pattern is symmetric with respect to the center of the channel.
To examine the statistical features of SDT, it is necessary to supplement the statistics from OT,[21,28] i.e., the initial sinuous streak and turbulent baseflow profiles are only set to be in the bottom half of the channel. The baseflow velocity can be modified by
Consider the initial streak in Eq. (
4) and spanwise perturbation in Eq. (
5), and only

will be chosen to establish a single sinuous streak on the bottom half of the channel. Since the turbulent state can be shifted from one wall to the other,
[21] when it happens, the quiet upper wall undergoes the transition for a while and both walls are turbulent. For this reason, the OT we use in this paper just means that the initial condition only contains a sinuous streak in the bottom half of the channel.
The statistic results of root-mean-square velocity fluctuations in the case of SDT and OT (ranging from t+ = 500 to 2480) are compared with the DNS results from Iwamoto et al.[35] in a regular fully developed turbulence (Reτ = 110) as shown in Fig. 6. In the case of SDT, the difference in velocity fluctuation between the case of
 and 1.0 is negligible. Note that the initial spanwise perturbation determines whether the turbulence can be sustained (Fig. 4), but cannot affect the behavior of statistics once the turbulence is sustained (Fig. 6), indicating that the initial spanwise perturbation is just an excitation to trigger the sustained turbulence at an initial stage. For the comparison among the SDT, OT, and DNS results from Iwamoto et al.[35] in the near-wall region (y+ = 0 ∼ 50), although there are some discrepancies, the general patterns are in good agreement. However, there are large discrepancies far away from the wall, and it is of interest that the normal velocity in the case of SDT sharply decreases to zero (v+ = 0) in the center of the channel (y+ = 80).
and 1.0 is negligible. Note that the initial spanwise perturbation determines whether the turbulence can be sustained (Fig. 4), but cannot affect the behavior of statistics once the turbulence is sustained (Fig. 6), indicating that the initial spanwise perturbation is just an excitation to trigger the sustained turbulence at an initial stage. For the comparison among the SDT, OT, and DNS results from Iwamoto et al.[35] in the near-wall region (y+ = 0 ∼ 50), although there are some discrepancies, the general patterns are in good agreement. However, there are large discrepancies far away from the wall, and it is of interest that the normal velocity in the case of SDT sharply decreases to zero (v+ = 0) in the center of the channel (y+ = 80).
The statistical profiles of streamwise vorticity (
 ), normal vorticity (
), normal vorticity (
 ), and spanwise vorticity (
), and spanwise vorticity (
 ) for SDT and OT triggered by
) for SDT and OT triggered by
 are shown in Fig. 7. In the near-wall region, there are some discrepancies, due most probably to the different initial condition set to be in the channel. For the case of OT, only a sinuous streak is set to be on the bottom half of the channel while the upper half is ‘quiet’. Once the turbulent state is shifted from one wall to the other, the vorticity kinetic energy can also be transfered. Thus, the vorticity statistics collected from both halves in the case of OT are relatively small compared with that of SDT. Far away from the wall, the normal vorticities (
are shown in Fig. 7. In the near-wall region, there are some discrepancies, due most probably to the different initial condition set to be in the channel. For the case of OT, only a sinuous streak is set to be on the bottom half of the channel while the upper half is ‘quiet’. Once the turbulent state is shifted from one wall to the other, the vorticity kinetic energy can also be transfered. Thus, the vorticity statistics collected from both halves in the case of OT are relatively small compared with that of SDT. Far away from the wall, the normal vorticities (
 ) between SDT and OT are in good agreement, but it is even more noteworthy that the streamwise vorticity (
) between SDT and OT are in good agreement, but it is even more noteworthy that the streamwise vorticity (
 ) and spanwise vorticity (
) and spanwise vorticity (
 ) in the case of SDT sharply decrease to zero in the center of the channel.
) in the case of SDT sharply decrease to zero in the center of the channel.
The above analyses indicate that the statistics of SDT is quite different from that of OT and the regular fully developed turbulence. The overall statistical profile of SDT is slightly larger in the near-wall region but smaller near the center of the channel than the statistic results from two other cases. The most striking feature of SDT is that the normal velocity (v+), streamwise vorticity (
 ), and spanwise vorticity (
), and spanwise vorticity (
 ) sharply decrease to zero in the center of the channel, indicating that the development of CS in the case of SDT is constrained near the center of the channel. To reveal the statistical regularity of SDT, the evolution of the CS including vortices and streaks in a phenomenological view will be presented in the next section.
) sharply decrease to zero in the center of the channel, indicating that the development of CS in the case of SDT is constrained near the center of the channel. To reveal the statistical regularity of SDT, the evolution of the CS including vortices and streaks in a phenomenological view will be presented in the next section.
4. Dynamics of CS in SDTWe will focus here on the instantaneous features of the streaks and vortex structures in the case of
 . This case is chosen because it needs a relatively short time for the initial flow to transit to fully developed turbulence compared with that of the case of
. This case is chosen because it needs a relatively short time for the initial flow to transit to fully developed turbulence compared with that of the case of
 . However, as mentioned below, similar evolution features can also be observed in other cases when
. However, as mentioned below, similar evolution features can also be observed in other cases when
 .
.
The unstable sinuous low-speed streak which is initially free of vortices can lead to the formation of the streamwise vortices by stretching an item of the streamwise vorticity, +∂u/∂x.[28] Our computations confirm this process. Since the CS from each wall is developed independently in the initial stage, only the CS in the bottom half of the channel is drawn in Fig. 8. The obvious behavior at the early stage is the occurrence of the streamwise vortices, which are attached to the streak in an overlapping pattern with alternating signs. With the spanwise perturbation in Eq. (5), the initial straight streaks oscillate and bend in the spanwise direction. When the bending degree of the streaks reaches a certain threshold, a stretching item of the streamwise vorticity, +∂u+/∂x+, develops near the bending part of the streak, leading to the generation and enhancement of the ‘zigzag’ streamwise vortices. On the one hand, when the streamwise vortices incline in the spanwise direction and tilt in the normal direction, the streaks oscillate and lift with the spatial variation of the streamwise vortices. On the other hand, the oscillated and lifted streaks can redistribute the flow and in turn feed the streamwise vorticity. As a result, positive feedback between low-speed streaks and streamwise vortices happens, which plays an important role in the self-sustaining behavior of turbulence.
As the upward-tilted angle of the streamwise vortex increases, the interaction between vortices from each wall occurs in the center of the channel. The Omega identification method (Ω method)[36] is used to track the surface of vortex structure. The vortex structure in such a method is defined when vorticity overtakes deformation (Ω > 0.5), where Ω is a ratio of vorticity squared over the sum of vorticity squared and deformation squared. The iso-surface of Ω = 0.53 is utilized to represent the vortex surface and further the vortex structure of the flowfield. Using this method, both strong and weak vortices can be well captured simultaneously. The evolution of the vortex structure identified by the Ω method is shown in Fig. 9.
To track the typical behavior of the vortex evolution, we will focus on the vortex structures drawn in opaque red color. At t+ = 154 (Fig. 9(a)), the quasi-streamwise vortices induced from each streak are inclined in the spanwise direction and tilted in the normal direction. Once both heads of quasi-streamwise vortices from each half of the channel approach closely to each other, they are connected in the center of the channel and thus form a hairpin-like vortex (Fig. 9(b)). As time goes on, the hairpin-like vortex grows outwards (Fig. 9(c)) and subsequently decays at t+ = 213 (Fig. 9(d)). When the quasi-streamwise vortices from both halves of the channel are strengthened and approach each other again (Fig. 9(e)), the next formation and evolution cycle of the NHV can be triggered (Fig. 9(f)–Fig. 9(h)).
The above analyses show that the vortex structures induced by the unstable sinuous streaks undergo the processes of inclining, tilting, colliding, and decaying. The most striking feature is the occurance of the hairpin-like vortices, which are distributed in the normal direction and straddled across both halves of the channel. It is of interest that the pattern of NHV is quite similar to that of the near-wall spanwise-disributed hairpins observed in the transitional and turbulent boundary layer. Our previous study[19] has shown that the formation of the spanwise-disributed hairpins is closely related to the interaction between two spanwise adjecent low-speed streaks. For the case of SDT in the present study, the interaction between two low-speed streaks can also happen but in the normal direction near the center of the channel. The evolutions of the low-speed streaks and vortex structure from t+ = 154 to t+ = 179 are shown in Fig. 10. Here, the low-speed streaks are characterized by the negative value of instantaneous streamwise velocity fluctuation, u+ = −1.3. At t+ = 154 (Fig. 10(a)), the low-speed streaks and vortex structures from each wall are developed independently, and no interaction occurs in the center of the channel. As time goes on, the low-speed streaks begin to lift and subsequently merge in the center of the channel (Fig. 10(b)). During that time, the downstream heads from each quasi-streamwise vortex are connected in the region where the low-speed streaks merge. Since the merging part of the streaks is located in the center of the channel where the baseflow velocity reaches to a maximal value (see Fig. 2), the merging part of the streaks develops faster in the downstream and the shape of the merging streak deforms into a U-like pattern (Fig. 10(c)). Accordingly, the hairpin-like vortex structure grows outwards and develops along with the U-like streak.
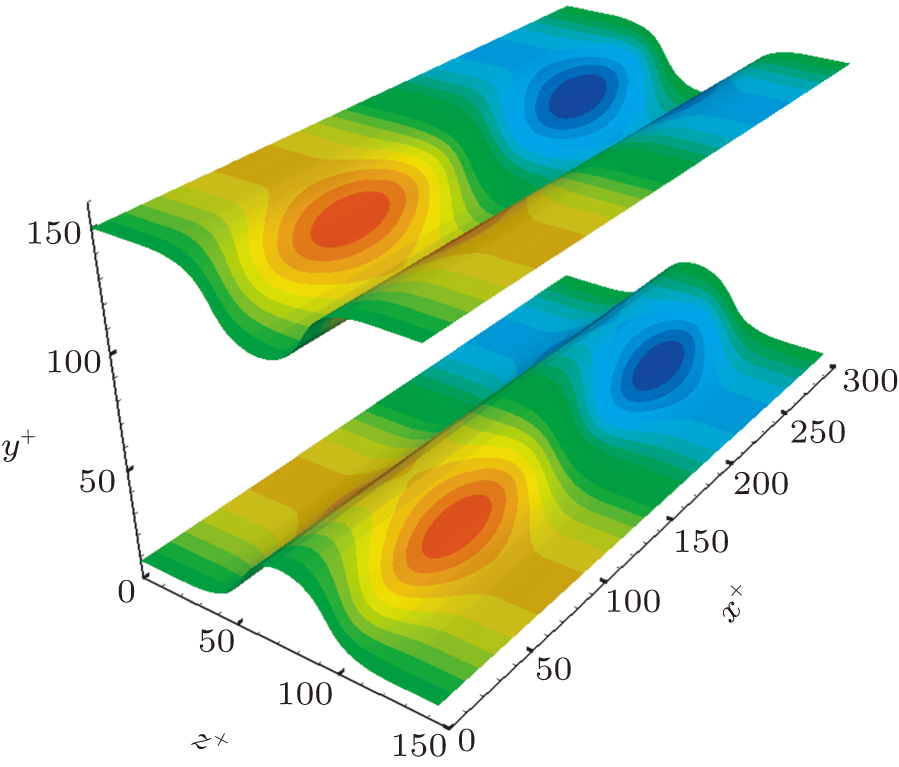
When the streaks merge in the center of the channel, the qusi-streamwise vortices are connected and deformed into a hairpin-like pattern. While when the shape of the merging streak deforms into a U-like pattern, the shape of the hairpin is also transfered into a U-like pattern. One can conclude that the formation and evolution of the NHV are closely related to the deformation of the streaks. Three-dimensional views of the NHV and the flowfields in the y–z plane (x+ = 240) at t+ = 162 are shown in Fig. 11. As the streaks merge in the center of the channel, the merging part of the streaks turns more compact and then moves in the spanwise direction, which leads to the enhancing of the ∂u+/∂z+ along the merging part of the streaks. Since the ∂u+/∂z+ is the major part of the normal vorticity (
 ), the normal vorticity contributed by ∂u+/∂z+ produces the head of the NHV. As a consequence, the quasi-streamwise vortices from each wall are connected by the normal vorticity at the center of the channel, leading to the generation of the NHV.
), the normal vorticity contributed by ∂u+/∂z+ produces the head of the NHV. As a consequence, the quasi-streamwise vortices from each wall are connected by the normal vorticity at the center of the channel, leading to the generation of the NHV.
The NHV can also be acquired in the case of
 , in which the initial amplitude of the sinuous streak is smaller than the above case as shown in Fig. 12. One can see that the formation of the NHV is the result of the normal collision between two low-speed streaks, indicating that such a structure is universal when the SDT is sustained. However, the formation of the NHV in the case of
, in which the initial amplitude of the sinuous streak is smaller than the above case as shown in Fig. 12. One can see that the formation of the NHV is the result of the normal collision between two low-speed streaks, indicating that such a structure is universal when the SDT is sustained. However, the formation of the NHV in the case of
 needs a relatively long time compared with that of
needs a relatively long time compared with that of
 , e.g. the NHV forms at t+ = 208 in the case of
, e.g. the NHV forms at t+ = 208 in the case of
 (Fig. 12(b)) while at t+ = 162 in the case of
(Fig. 12(b)) while at t+ = 162 in the case of
 (Fig. 10(b)). As mentioned in Fig. 4, the increasing of the initial spanwise perturbation amplitude of the sinuous streak can lead to the fast growing of the streamwise vortices. With the fast growing of the streamwise vortices, the low-speed streaks lift rapidly and the collision between two streaks occurs quickly. For this reason, the NHV forms earlier as the initial amplitude of the sinuous streak increases.
(Fig. 10(b)). As mentioned in Fig. 4, the increasing of the initial spanwise perturbation amplitude of the sinuous streak can lead to the fast growing of the streamwise vortices. With the fast growing of the streamwise vortices, the low-speed streaks lift rapidly and the collision between two streaks occurs quickly. For this reason, the NHV forms earlier as the initial amplitude of the sinuous streak increases.
The above analyses show that the formation of NHV is closely related to the cross-interaction of the low-speed streaks derived from the opposite half of the channel. Firstly, when the two low-speed streaks lift to the center of the channel, they merge near the center of the channel. Secondly, the merging part of the low-speed streaks which are surrounded by the high-speed flows can lead to the shear effect, and thus giving rise to the normal vorticity. Finally, the normal vorticity is connected by the quasi-streamwise vortices near each wall, and thus giving birth to the NHV. It is worth noting that such a hairpin formation mechanism is nearly the same as that of the spanwise-distributed hairpin vortex, which we have addressed before,[19] that is, the formation of the NHV and the spanwise-distributed hairpin vortex are both caused by the collision between the low-speed streaks. However, unlike the emergence of a spanwise-distributed hairpin vortex, which is caused by the spanwise collision between two spanwise-aligned low-speed streaks in a flat plate, the NHV, triggered by the normal collision between two normal aligned low-speed streaks, can only exist in channel flow which has two walls.
Figure 13 shows the enlargement of wall skin frictions on Fig. 4 from t+ = 0 to t+ = 800 in the case of
 . It is observed that the wall skin friction reaches to the first peak at t+ = 179 and arrives at the second peak at t+ = 616. Interestingly, the vortex structures at those times are shaped in NHV (Figs. 9(c) and 9(g)), which means that the vortex connection and the newly formed NHV indeed have an influence on the sudden surge of wall skin friction.[23] In this paper, the mechanism of the vortex connection on the wall skin friction is not studied in detail, but the visualization (e.g., figure 10) suggests that when the vortex connection happens and the NHV forms, the low-speed streaks lift to a high level so that the wall skin friction increases to a high value.
. It is observed that the wall skin friction reaches to the first peak at t+ = 179 and arrives at the second peak at t+ = 616. Interestingly, the vortex structures at those times are shaped in NHV (Figs. 9(c) and 9(g)), which means that the vortex connection and the newly formed NHV indeed have an influence on the sudden surge of wall skin friction.[23] In this paper, the mechanism of the vortex connection on the wall skin friction is not studied in detail, but the visualization (e.g., figure 10) suggests that when the vortex connection happens and the NHV forms, the low-speed streaks lift to a high level so that the wall skin friction increases to a high value.
Our previous studies[19] have shown that the legs, necks, and head of the spanwise-distributed hairpin are mainly contributed to by the streamwise vorticity (
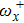 ), normal vorticity (
), normal vorticity (
 ), and spanwise vorticity (
), and spanwise vorticity (
 ), respectively. In the present study, the NHV can be viewed as the spanwise-distributed hairpin that rotates 90 degrees around the x axis, and the role of the vorticity in the hairpin can also be changed accordingly. Figure 14 shows the NHV colored by the local values of streamwise vorticity (Fig. 14(a)), normal vorticity (Fig. 14(b)), and spanwise vorticity (Fig. 14(c)) in the case of
), respectively. In the present study, the NHV can be viewed as the spanwise-distributed hairpin that rotates 90 degrees around the x axis, and the role of the vorticity in the hairpin can also be changed accordingly. Figure 14 shows the NHV colored by the local values of streamwise vorticity (Fig. 14(a)), normal vorticity (Fig. 14(b)), and spanwise vorticity (Fig. 14(c)) in the case of
 . One can see that the legs, necks, and head of the NHV are mainly contributed to by the streamwise vorticity, spanwise vorticity, and normal vorticity, respectively. Apparently, the roles of the vorticity in the head and necks of the NHV have been changed compared with the scenario of a regular spanwise distributed hairpin, that is, the head (necks) of the NHV plays the same role as the necks (head) of the spanwise-distributed hairpin vortex. Furthermore, the distribution of the vorticity on the NHV is coincident with the statistical vorticity profiles in Fig. 7, only the statistical values of the normal vorticity exist near the center of the channel but the statistical values of the streamwise and spanwise vorticity decrease to zero. Since the upper and bottom streaks are symmetric with respect to the center of the channel, their cross-interaction parts are always in a symmetric pattern (Fig. 11); such a symmetric pattern of the merged streak can only result in the production of the normal vorticity in the center of the channel.
. One can see that the legs, necks, and head of the NHV are mainly contributed to by the streamwise vorticity, spanwise vorticity, and normal vorticity, respectively. Apparently, the roles of the vorticity in the head and necks of the NHV have been changed compared with the scenario of a regular spanwise distributed hairpin, that is, the head (necks) of the NHV plays the same role as the necks (head) of the spanwise-distributed hairpin vortex. Furthermore, the distribution of the vorticity on the NHV is coincident with the statistical vorticity profiles in Fig. 7, only the statistical values of the normal vorticity exist near the center of the channel but the statistical values of the streamwise and spanwise vorticity decrease to zero. Since the upper and bottom streaks are symmetric with respect to the center of the channel, their cross-interaction parts are always in a symmetric pattern (Fig. 11); such a symmetric pattern of the merged streak can only result in the production of the normal vorticity in the center of the channel.
For the regular spanwise-disributed hairpin vortex, the ejections of the fluids occur inside the hairpin toward the normal direction away from the wall, while the sweeps of the fluids occur outside the hairpin toward the wall. For the NHV, the motion of the fluid can also be changed because of the changing angle of the hairpin. Figure 15 shows the NHV colored by local values of streamwise velocity (Fig. 15(a)), normal velocity (Fig. 15(b)), and spanwise velocity (Fig. 15(c)) in the case of
 . It can be seen that the u+ is distributed near the necks of the NHV and its value reaches a minimum value in the center of the channel (Fig. 15(a)). While the v+ is distributed on the legs of the NHV and its value decreases to zero in the center of the channel (Fig. 15(b)). For the spanwise velocity (w+) in Fig. 15(c), the positive and negative spanwise velocity are located inside and outside of the NHV, respectively. This suggests that the spanwise velocity on the NHV plays the same role as the normal velocity in the spanwise-distributed hairpin. Furthermore, as mentioned in Fig. 14, only the normal vorticity exists in the center of the channel, such a vorticity can only produce the streamwise and spanwise velocity in the x–z plane in the center of the channel (Fig. 16). For this reason, the normal velocity sharply decreases to zero in the center of the channel, which is coincident with the statistical velocity profile in Fig. 6.
. It can be seen that the u+ is distributed near the necks of the NHV and its value reaches a minimum value in the center of the channel (Fig. 15(a)). While the v+ is distributed on the legs of the NHV and its value decreases to zero in the center of the channel (Fig. 15(b)). For the spanwise velocity (w+) in Fig. 15(c), the positive and negative spanwise velocity are located inside and outside of the NHV, respectively. This suggests that the spanwise velocity on the NHV plays the same role as the normal velocity in the spanwise-distributed hairpin. Furthermore, as mentioned in Fig. 14, only the normal vorticity exists in the center of the channel, such a vorticity can only produce the streamwise and spanwise velocity in the x–z plane in the center of the channel (Fig. 16). For this reason, the normal velocity sharply decreases to zero in the center of the channel, which is coincident with the statistical velocity profile in Fig. 6.
5. Concluding remarksBy setting two symmetric low-speed streaks to be on the opposite halves of the channel, the evolution of the low-speed streaks and the vortices induced by unstable streaks are investigated by DNS. The Omega method is used to track the vortex surface. The results show that the NHV can be induced by the cross-interaction between the upper and bottom low-speed streaks and the occurrence of NHV can lead to the sudden surge of the wall skin friction. The cross-interaction of the streaks produces a normal vorticity that connects the heads of the near-wall opposite-rotating quasi-streamwise vortices, and thus giving birth to the NHV. The pattern of NHV can be viewed as a regular hairpin vortex that rotates 90 degrees around the x axis, so that the roles of the vorticity in the head and necks of the NHV are changed compared with a regular spanwise-distributed hairpin vortex. Since the upper and bottom low-speed streaks are symmetric with respect to the center of the channel, their interaction can only produce the normal vorticity in the center of the channel. As a result, the values of the normal velocity as well as the streamwise and spanwise vorticity sharply decrease to zero in the center of the channel in which the development of CS is constrained.