† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. U1738120 and 11474326).
Energy dissipation is one of the most important properties of granular gas, which makes its behavior different from that of molecular gas. In this work we report our investigations on the freely-cooling evolution of granular gas under microgravity in a drop tower experiment, and also conduct the molecular dynamics (MD) simulation for comparison. While our experimental and simulation results support Haff’s law that the kinetic energy dissipates with time t as E(t) ∼ (1 + t/τ)−2, we modify τ by taking into account the friction dissipation during collisions, and study the effects of number density and particle size on the collision frequency. From the standard deviation of the measured velocity distributions we also verify the energy dissipation law, which is in agreement with Haff’s kinetic energy dissipation.
Granular gas is a dilute ensemble of grains interacting by dissipative collisions. This dissipative nature of particle interactions determines its ensemble properties, and distinguishes it from molecular gas. The most prominent feature is granular cooling so that the system loses kinetic energy permanently, with no external energy input. From a homogeneous excited-state, the system enters into an initial period of homogeneous energy loss, and later grains can spontaneously cluster.[1–17] Theoretical modeling,[18–29] and simulation investigations[20–22,24,28,30–39] are based on simplifications and assumptions of grain properties. Quantitative experiments are very much needed for better understanding of fundamental features of such ensembles.[40–43] In this work we report our investigations on the freely-cooling evolution of granular gas under microgravity in a drop tower experiment, and conduct the molecular dynamics (MD) simulation for comparison.
In order to investigate the energy loss due to grain-grain collisions in steady excitation and during free cooling, experiments need to counterbalance the gravitational force to float the particles.[14,40] In 2008, Maaß et al. used magnetic forces to make the granular particles float in a container.[40] In their experiment, diamagnetic particles were chosen. The total energy of a particle in a magnetic field B is U = −χVB2/2μ0 + mgz,[44] where U is the potential energy of the particle, χ is the magnetic susceptibility, V is the volume of the particle, μ0 is vacuum permeability, m is the mass of particle, g is the gravity, and z is the position of particle in the z direction. Since
Tatsumi et al. reported in 2009 the first microgravity experimental investigations on a freely cooling granular gas system. Their microgravity experiment was performed during parabolic flight. They studied the kinetics of both freely cooling and steadily driven granular gas system in quasi-two-dimensional cells under micro-gravity.[41] Due to the g-jitter of the parabolic flights, Tatsumi et al. could observe only within one second of the cooling process. Their granular temperature decays as Tg = T0 (1 + t/τ)−2, which is consistent with Haff’s law that E(t) ∼ (1 + t)−2.
Very recently Kirsten Harth et al. studied free cooling of a granular gas of rod-like particles in microgravity. For rod-like particles they found that the law of E(t) ∼ t−2 is still robust.[43] A slight predominance of translational motions, as well as a preferred rod alignment in the flight direction were also found.
These previous studies mainly concerned the form of kinetic energy dissipation with time. In this paper, we conduct a micro-gravity experiment in a Bremen Drop Tower and compare the results with simulations to verify the validation of more detailed factors (such as restitution coefficient, number density, particles size) affecting Haff’s law. We take into consideration the collision friction to modify the model for the characteristic decay time τ. Experimental and simulation results show that the average speed of all particles in granular gas decays with time t as v ∼ (1+t/τ)−1 and the kinetic energy decays with time t as E(t) ∼ (1+t/τ)−2 as predicted in Haff’s law. In our 5 second cooling observation time we, however, do not see the clustering mode as reported in Maaß’s research.
Haff’s theory about freely cooling granular is based on the classical thermodynamics.[18,19] There are several assumptions to simplify the analysis of the freely cooling process of dilute granular gas. Firstly, the restitution coefficient is constant for each collision among particles. Secondly, the granular gas system must be homogeneous, so the mean free path is meaningful in the analysis and can be used to calculate the collision frequency. Thirdly, only collisions among particles contribute to the energy dissipation in the theory, while the part due to friction is not taken into account. Fourthly, the size of particles is relatively small compared with the mean free path.
The mean free path of particles in dilute and homogeneous granular gas is λ = 1/(nσ), where n is the number density and σ = π(2R)2 is the cross section of particle respectively. Here R is the particle radius. The kinetic energy E of one-unit volume of granular gas is proportional to 






 |
The change of kinetic energy per unit time equals the loss of the energy per unit time due to collisions between particles,
 |
By solving Eq. (
 |
 |
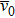
The kinetic energy E is proportional to 
 |
After a duration of τ since the granular gas begins to cool freely, the average velocity of the system will drop by half as given in Eq. (
 |
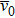
Most of the previous research has mainly been concerned with the form of Eq. (
To study the granular gas cooling behavior on the ground, gravity has to be counteracted by an external force, like buoyancy in liquid, an electric or magnetic field force. For example, Maaß et al. used the magnetic gradient to make the diamagnetic particle float.[40] Soichi Tatsumi et al. were the first to attempt microgravity experiment studying the freely cooling granular gas behavior in parabolic flights.[41] However, due to the g-jitter during the flights, their cooling observations were no longer than 1.6 s. In the present work, we achieve microgravity in a Bremen Drop Tower. The Bremen Drop Tower, with a height of 146 meters, provides up to 10−6-g microgravity condition with a duration as long as 9.3 s.
In our experiments, the catapult operation mode with a weightless duration of 9.3 s was adopted. By this means, a drop capsule [see Figs.
 | Fig. 1. (color online) (a) Experiment setup carrying drop capsule; (b) experiment platform composed of the power system and the setup; (c) sketch of the experimental setup. |
The size of the sample cell is 150 mm × 50 mm × 10 mm. Three sub cells are separated by two pistons as is shown in Fig.
| Table 1. Key parameters in each group of experiments. . |
The experimental images are captured by a high-speed camera of 500 fps. Each frame of the image is of 512 × 512 pixels. The resolution of experimental images is about 0.3 mm/pixel, therefore the particle sizes with diameters 2 mm and 2.5 mm are about 6–7 pixels and 8–9 pixels, respectively. However, since we have only one camera, we can observe only a two-dimensional projection of the particle three-dimensional motion. Some trajectories of two overlapped particles may not be identified. Over exposure in one of the cell corners also hinders tracing particles in that area. Despite of all these, we can trace more than 95 percent of the total particles.
Figure
 | Fig. 3. (color online) (a) Traces of all particles in the freely cooling process; (b) Demo of few traces of particles. |
The speed of each particle vi is calculated from 




 | Fig. 4. (color online) (a) Average speed and (b) average kinetic energy of particles as a function of time. |
| Table 2. Parameters fitted by Eq. ( |
In our experiments, collisions with the two pistons provide particles with initial velocities in the x direction. Figure 


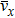


 |
 |
 | Fig. 5. (color online) Average speeds in the vertical (x, black curves) direction and horizontal (y, red curves) direction decaying with time. |
The kinetic energy E is proportional to the square of the average speed of particles 
Considering the limitation of the experimental opportunities, we perform simulations based on the discrete elements method (DEM).[45,46] The cell size in the simulation is fixed at 10 cm×10 cm×10 cm. In Haff’s theory, the contribution of the energy dissipation caused by friction during collision between particles is not considered; however, in reality, friction exists. In this simulation, the influence of friction is considered.
Figure
 | Fig. 6. (color online) Average speeds decaying with time t with (blue dot) and without (green dot) condisering friction. |
Figure
 | Fig. 7. (color online) Simulated τ versus the restitution coefficient e with no friction. Inset shows the linear relationship between (1 − e2)−1. |
Figure
 |
 | Fig. 8. (color online) Simulated τ versus restitution coefficient e with friction. Inset shows linear relationship between (1 − e2 + γ)−1 and τ. |
The red curve in Fig.
From Eq. (

 | Fig. 10. (color online) Decay time τ as a function of number density n. The inset shows the linear relationship between n and 1/τ. |
For a conservative classical ideal gas system in equilibrium state, the velocity distribution of each dimension follows the normal distribution. But it is still not widely accepted that what law the velocity distribution of a dissipative system like granular gas obeys. Figure
We recall that the state of energy equipartitions for freely cooling granular gas will be reached even if the symmetry is broken at the initial time. Our numerical results show that the freely cooling granular gas not only follows Haff’s law but also has two intrinsic properties, namely the energy equipartition and the normal velocity distribution.
Our experimental and simulation results on the granular gas free cooling process support Haff’s law that the kinetic energy dissipates with time t as E(t) ∼ (1+t/τ)−2. The effects of particle number density and the particle size on τ, due to the rotation and friction during collision, are studied in simulation. A modified τ is given to take into account the dissipation due to frictions. The collision frequency affected by the number density and particle size is discussed. From the standard deviation of the velocity distribution we also verify the energy dissipation law, showing its good consistence with Haff’s Kinetic energy dissipation.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |







