† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11604385 and 91436103).
Based on relativistic wave functions from multiconfiguration Dirac–Hartree–Fock and configuration interaction calculations, E2 and M1 transition probabilities of 2p3 4S3/2–2p3 2D3/2,5/2 are investigated in the nitrogen-like sequence with 7 ≤ Z ≤ 16. The contributions of the electron correlations, Breit interaction, and the quantum electrodynamic (QED) effects on the transition properties are analyzed. The present results can be used for diagnosing plasma. In addition, several N-like ions can also be recommended as a promising candidate for a highly charged ion (HCI) clock with a quality factor (Q) of transition as high as 1020.
Optical frequency standard has truly made impressive advances over the past decade. Presently lattice clocks have demonstrated a stability at the 10−18 level (Yb,[1] Sr[2]). Such a high precision has a profound influence on testing the spatiotemporal variation of fundamental constants and searching for dark matter. It is also expected to replace the cesium fountain clock to define the international unit “second”. However, an optical clock is very sensitive to environmental perturbations and the blackbody radiation (BBR), electric quadrupole frequency shift, Zeeman shifts in a magnetic field, ac-Stark shifts induced by laser, etc., all of which will contribute to the uncertainty of the “Clock”. Fortunately, the new generation of nucleus clocks and highly charged ion (HCI) clocks are much less affected by these factors. 229Th nuclear clock utilizing the environment-resistant neutron transition in nucleus is estimated to have a fractional accuracy at the 10−19 level.[3] Since the neutron is tightly wrapped in the nucleus, the transition is hardly affected by external factors. Like the nuclear clock, the electron cloud of HCIs has a shrunken size, which causes a small frequency uncertainty with an accuracy below 10−19.[4] The breakthrough of quantum-logic spectroscopy, sympathetic laser cooling, and ion crystal trapping techniques[5] has provided a possibility to realize this kind of new ultra-precise optical frequency standard. It has become an urgent task to find candidates that are easy to realize experimentally and have high quality factors and low uncertainty. Yudin[6] estimated the magnetic-dipole (M1) transitions in HCIs with a single s-valence electron, a single p-valence electron, and two p-valence shell electrons, which can be considered as high-accuracy candidates for HCIs clocks. Yu[7] have investigated M1 transitions in the Al-like 51 V10+, 53Cr11+, 55Mn12+, 57Fe13+, 59Co14+, 61Ni15+, and 63Cu16+ ions as possible clock frequency standards. Liu[8] recommended Cu10+ and Zn11+ as candidates for HCI clocks. In this paper, we propose that HCI with three p-valence shell electrons (nitrogen-like sequence) be the candidate. In addition, the transition spectrum also has an important application in plasma diagnosis. Some transitions for the N-like ions falling in the UV spectral range have been observed by the SOHO/SUMER instrument in the solar spectrum, which plays an important role in the study of solar internal activity.[9]
Owing to the importance in astrophysics and plasma physics, a lot of theoretical and experimental researches on the nitrogen-like sequence have been performed in recent years. Edlén[10,11] observed the transition spectra among the configurations 2s22p3, 2s2p4, and 2p5 of the nitrogen-like sequence in tokamak plasma, and he derived and recommended the level values for ions in a range of Z = 10–36 by comparing with the corresponding theoretical values from the tables of Cheng.[12] Recently, the transitions of 2s22p3–2s2p4 in nitrogen-like tungsten ion have been measured by electron beam ion traps (EBITs).[13] Träbertet[14,15] measured the lifetime of the 2s22p3 2P1/2,3/2 levels of S X in a heavy-ion storage ring, while the lifetime of highly ionized silicon was measured by using beam-foil spectroscopy.
With the development of the theoretical methods in atomic physics and the capacity of computers, nitrogen-like sequences have been widely studied. Zeippen,[16,17] Becker,[18] and Godefroid[19] successively gave the computing results using the multiconfiguration Hartree–Fock method with relativistic corrections in the Breit–Pauli approximation (MCHF-BP). Merkelis[20] used second-order many-body perturbation theory (MBPT) with relativistic corrections in the Breit-Pauli approximation to calculate the transitions of ions in a range of Z = 10–30. Using relativistic multi-reference Møller–Plesset perturbation theory (MRMP), Vilkas[21] calculated the energy levels and transition probabilities of some nitrogen-like ion sequences. Froese Fischer and Tachiev[22,23] published their analysis of fine structure splitting and transition rates for the ground configuration in the nitrogen-like sequence up to Zn XXIV using the multiconfiguration Hartree–Fock with relativistic corrections in the Breit-Pauli approximation (MCHF-BP), which has become an authoritative reference for others. Wang[24] used the multiconfiguration Dirac–Hartree–Fock self-consistent field method and the relativistic configuration interaction method (MCDHF + RCI) with quantum electrodynamics corrections to calculate the fine-structure energy levels of the ground-state configuration up to Z = 22. The influence of Breit interaction together with the quantum electrodynamic (QED) effects for level splittings was also analyzed in the work. With the same method, Rynkun[25] evaluated E1, M1, E2, and M2 transition rates, weighted oscillator strengths, and lifetimes for the states of the 2s22p3, 2s2p4, and 2p5 configurations in all nitrogen-like ions between F3+ and Kr30+ but did not present the forbidden transition rates 2p3 4S3/2–2p3 2D3/2, 5/2. Focusing on the scaling law, Han[26] calculated transition probabilities in 2p3 configuration of a nitrogen-like sequence with 7 ≤ Z ≤ 79. Neither the high order correlation effect or the QED effect in the calculation was taken into account. In the database of NIST, most of forbidden transition rates 2p3 4S3/2–2p3 2D3/2, 5/2 are theoretical data cited from Zeippen,[17] Merkelis,[20] Froese Fischer and Tachiev.[22,23] The data of Ne4+ were given by Garstang in 1960,[27] while F3+ and P9+ data were cited from Naqvi’ working in 1951.[28]
In this paper, based on relativistic wave functions from multiconfiguration Dirac–Hartree–Fock and configuration interaction calculations, E2 and M1 transition probabilities of 2p3 4S3/2–2p3 2D3/2,5/2 are investigated in the nitrogen-like sequence with 7 ≤ Z ≤ 16. The contributions of the electron correlations, Breit interaction, and the quantum electrodynamic effect are analyzed. The calculation results show the Q factor goes up to 1020, and we recommend F2+, Ne3+, and Na4+ as the candidates for the HCI clocks.
The multiconfiguration Dirac–Hartree–Fock method was used in the present work. The Dirac–Coulomb Hamiltonian has the form as
 |

The atomic state function (ASF) was obtained as a linear combination of symmetry adapted configuration state functions (CSFs) with the same parity P, the total angular momentum J, and its projection along the z direction MJ, which is written as
 |
In subsequent relativistic configuration interaction (RCI) calculations, the transverse photon interaction (Breit interaction) was included in the Hamiltonian, while cj could be optimized. The Breit interaction in the low-frequency approximation (ωij → 0) is taken into account in the procedure, which has the following form:
 |
 |
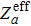
 |
 |
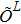
 |
 |
Furthermore, the lifetime τ of the upper state i can be determined by
 |
All calculations were performed with the GRASP2K code, provided by Jönsson, Froese Fischer, and Grant et al.[31] The GRASP2K package is based on the multiconfiguration Dirac–Hartree–Fock (MCDHF) method. The package consists of a number of application programs and tools to compute approximate relativistic wave functions, energy levels, hyperfine structures (HFS), isotope shifts (IS), Landé gJ-factors, interactions with external fields, angular couplings for labelling purposes, and transition energies and probabilities for many-electron atomic systems.
As shown in Fig.
To describe effectively the important zero-order correlations in the first step, we calculated the contributions of the individual electron pairs separately in the DHF. All occupied orbitals were optimized, but kept frozen in the subsequent steps. In this work, {1s22s22p3} was chosen as the reference state for the three concerned 2p3 4S3/2, 2p3 2D3/2, 5/2 states.
The first-order correlation is considered in the MCDHF procedure usually. We devoted to finding a simplified calculation by RCI. In the present work, valence, core–valence, and core–core correlation effects were included. To monitor the convergences of the calculated energies and transition parameters, the active sets were increased in a systematic way by adding the layers of correlation orbitals. The configuration expansions for the states belonging to {1s22s22p3} were obtained by single-double (SD) excitations to active sets with principal quantum numbers n ≤ 9 and angular symmetries l ≤ 6. The amount of computation of MCDHF is quite large if SD excitations including valence, core–valence, and core–core correlation effects go through all the shells. By comparing the MCDHF models of SD excitations including different shells with RCI models containing a diverse combination of wave function and configuration, the important correlation effects in the optimization of orbitals can be differentiated. The amount of computation can be greatly reduced later using appropriate RCI models to obtain the best result. As shown in Fig.
The higher-order correlation contains the correlations of triple, quadruple or more excitations. We use the SD excitations of a multireference (MR) approach to involve the important higher-order correlations into the RCI procedure. Then {1s22p5, 1s22s2p33d, 1s22 22p3d2} will be selected as the multireference set. The number of configurations expands up to 6.9 × 105 from 3.0 × 105 in first-order correlations considering a valence correlation for MR. This model is labeled as MR RCI.
Finally, the Breit interaction and the leading QED effects were considered by MR RCI computation, which are labeled as “+B” and “+Q”, respectively. E2 and M1 transition probabilities of 2p3 4S3/2–2p3 2D3/2,5/2 were computed in the nitrogen-like sequence with 7 ≤ Z ≤ 16.
In order to verify the validity of the computational model, we show the calculated forbidden transition probabilities and excitation energy of Na V of diverse computational models in Table
| Table 1. Excitation energies (ΔE in unit of cm−1), M1 transition probabilities (AM1 in unit of s−1), and E2 transition probabilities (AE2 B and AE2 C in unit of s−1) of Na V 4S3/2–2D5/2 with diverse computational models. Notations “C” and “B” represent results of AE2 in the Coulomb and Babushkin gauges, respectively. A number in a square bracket represents the power of 10. Δ represents the difference between AE2 B and AE2 C. . |
The results for the excitation energies and the forbidden transition probabilities of the 2p3 4S3/2–2p3 2D3/2,5/2 transition in the N-like ions with 7 ≤ Z ≤ 16 are presented in Tables
| Table 2. Excitation energies (ΔE) of the 2p3 4S3/2–2p3 2D3/2,5/2 transition in N-like ions with 7 ≤ Z ≤ 16. Label denotes 4S3/2 − 2 D5/2 as A, and 4S3/2–2D3/2 as B. . |
| Table 3. M1 transition probabilities (AM1 in unit of s−1 ) and E2 transition probabilities (AE2 B and AE2 C of 2p3 4S3/2–2p3 2D5/2 in unit of s−1). Notations “C” and “B” represent results of AE2 in Coulomb and Babushkin gauges, respectively. A number in square brackets represents the power of 10. . |
| Table 4. M1 transition probabilities (AM1 in unit of s−1) and E2 transition probabilities (AE2 B and AE2 C of 2p3 4S3/2–2p3 2D3/2 in unit of s−1). Notations “C” and “B” represent results of AE2 in Coulomb and Babushkin gauges, respectively. A number in square brackets represents the power of 10. . |
| Table 5. Excitation energies (ΔE in unit of cm−1), the transition wavelengths λ in unit of nm, total transition probabilities (A in unit of s−1), quality factor Q of the forbidden transition probabilities of the 2p3 4S3/2–2p3 2D3/2,5/2 transition in N-like ions with 7 ≤ Z ≤ 16, line strengths (SE2, SM1 for E2 and M1), line intensity ratios (A (4S3/2–2D5/2)/A (4S3/2–2D3/2)). A number in square brackets represents the power of 10. (Label denotes 4S3/2–2D5/2 as A and 4S3/2–2D3/2 as B). . |
The transition probabilities for the ions are summarized in Table
Out of the interest of the plasma diagnostic process and the candidates of the HCIs clocks, we have investigated the M1 and E2 forbidden transition properties of the fine-structure in 2p3 4S3/2–2p3 2D3/2,5/2 state for the N-like ions for 7 ≤ Z ≤ 16 with the MCDHF method and configuration interaction calculations. The results of the excitation energies are in good agreement with NIST data. The contributions of the electron correlations, Breit interaction, and the leading QED effects are analyzed. It is shown that the good treatment of electron correlation and inclusion of the Breit interaction are essential for reliably predicting the transition properties for these ions. In choosing candidates for HCI clocks from the N-like ions in 7 ≤ Z ≤ 16, F2+, Ne3+, and Na4+are recommended out of the overall consideration of the Q factor, the lifetime of the clock state, and the wavelength and linewidth of the lasers for experiments.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] |



