Quantum secret sharing (QSS)^[1] is one of the most attractive research branches in quantum cryptography,^[1–5] which allows a secret of the dealer to be shared among many agents, and only the authorized groups of agents can reconstruct the secret information. In 1999, Hillery et al.^[1] proposed the first QSS protocol based on the GHZ states. From then on, QSS has received widespread attention and a range of QSS protocols^[6–24] have been presented in succession, which can be classified purposefully as two categories:^[1] one is to share classical information and the other is to share quantum information (secret sharing of quantum state).

Although varieties of QSS protocols have been presented in recent decades, how we add or delete agents as well as update secret or sub-secrets (the messages held by agents) in the QSS protocol is still a novel field. Here we call it the problem of dynamic parameter update, and refer to this kind of protocol as a dynamic quantum secret sharing (DQSS) protocol. In 2011, Yang et al.^[21] presented a DQSS protocol for the member expansion based on the ideas of the classical Shamir scheme.^[25] However, in this protocol, the cost of quantum resource and the number of the transmission for member expansion are considerable. In 2012, Jia et al.^[22] presented two DQSS protocols based on starlike duster states, which allows the agent group to change during the procedure of sharing classical and quantum secrets. But these protocols also consume too many quantum resources, and they cannot update secret or sub-secrets dynamically like Yang’s protocol can. In 2013, another DQSS protocol was presented by Hsu et al.^[23] based on the entanglement swapping of EPR pairs, which can allow an agent to be added or deleted. However, it has been proved that the protocol cannot resist a collective attack.^[26] In 2016, a multi-group DQSS protocol was presented by Liu et al.^[24] based on single photons, which is more flexible and practical, but it is fitter for sharing secrets between a boss and some groups.

In this paper, we firstly propose the two-particle transform of Bell states to solve the problems of dynamic parameter update in QSS, which can perform different local unitary operations separately on two particles of Bell states. According to this transform, we present a DQSS protocol realizing the functions of adding or deleting agents and updating sub-secrets or secrets. The new protocol can resist attacks such as a dense-coding attack, compound entanglement swapping attack, and a cheating attack from a dishonest agent. Based on the high coding-efficiency of a two-particle transform of Bell states and the exchangeability of the phase shift operation set, the number of coding operations is only half of the secret bits, and the computation complexity of the secret reconstruction is O(n − 1). Furthermore, we take advantage of the new protocol to establish the dynamic secret sharing of the quantum state (DSSQS) protocol for the two-particle maximum entangled states.

We propose a method by the name of two-particle transform of Bell states, which can perform the different local unitary operations chosen by the dealer and agents separately from the Pauli operations and the 3-element phase shift operations^[27] on two particles of Bell states. Firstly, we prove the following conclusions.

According to theorem 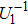1, when designing the QSS protocol, we can regard U₁ as the compound operation on photon t performed by agents, and U₂ as the encoding operation of the secret on photon h performed by the dealer, and as the reverse compound operation on photon t performed by agents.

It is obvious that there are three properties on this transform:

(i) Independence of operations

Based on Theorem 1, the operation on one particle of Bell states has no influence on the operation on the other particle. Thus we can make use of this property to design the DQSS protocol.

(ii) Nonlocal correlation of measuring results

Based on the nonlocal space properties of quantum entangled states, the local operation performed on one particle of Bell states can be deduced just by measuring collectively on the Bell states. Thus when we design the QSS protocol, the property can ensure the security of the protocol: if the unauthorized groups cannot obtain enough messages of agents’ operations (as the sub-secrets), they cannot deduce the encoding operation (as the secret) by measuring.

(iii) High coding-efficiency

Based on the quantum high-coding scheme,^[28] the Pauli operations on 1 qubit can code 2 bit classical messages; that is to say, the Pauli operation I(σ_x, σ_z, iσ_y) corresponds to the two classical bits “00” (“10”,“01”,“11”). In the QSS protocol, if the number of classical secrets is n bits, the number of coding operations is ⌈n/2⌉, as many as half of the secret bits.

The new DQSS protocol consists of two parts as follows.

3.1. Process of secret sharing

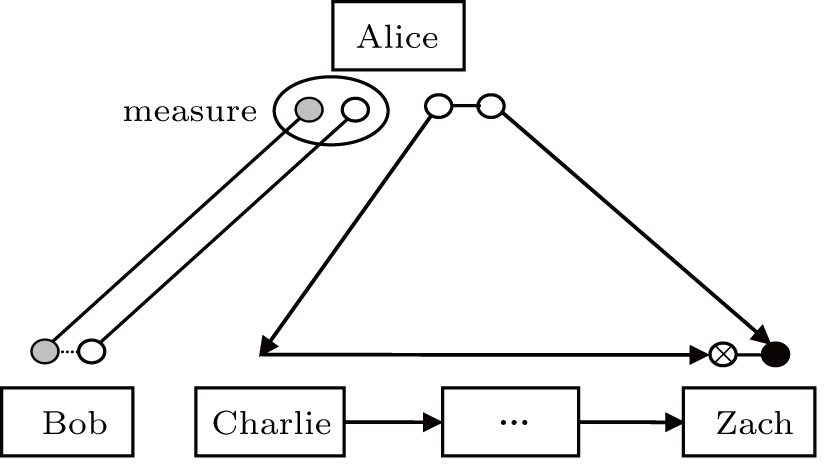
Suppose that Alice is the dealer with her secret, the set of agents is B = {Bob, Charlie, . . ., Zach}, and the number of B is n. The purpose of the protocol is that Alice shares a secret M among these agents in B, and all the agents can only reconstruct the secret information by cooperating with each other.

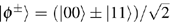
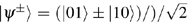
i) Alice prepares k pairs of Bell states (i.e., |φ₁⟩_th, . . ., |φ_k⟩_th) randomly from {|ϕ⁺⟩, |ϕ⁻⟩, |ψ⁺⟩, |ψ⁻⟩}, here , . Then she stores all the photons h of these Bell states (as H-sequence) in her laboratory, and sends all the photons t (as T-sequence) to Bob.

ii) After receiving the T-sequence, Bob firstly ascertains whether it is the single-photon sequence by using the photon number splitter (PNS: 50 = 50) or photon beam splitter(PBS: 50 = 50), etc. If not, he aborts the communication; otherwise, he performs the local unitary operations U(α_i) (i = 1, 2,. . ., k) respectively on the photon t_i of the T-sequence, which is chosen randomly from the phase shift operation set S = {U(0),U(2π/3),U(4π/3)}.^[27] Here

Then Bob stores all of the operation messages as his sub-secret, and sends the T⁽¹⁾-sequence (transformed from T-sequence) to Charlie.

iii) Charlie and the other agents perform procedures similar to Bob till the last agent Zach finishes his operations. At that time, Zach stores all the photons of the T⁽ⁿ⁾-sequence in his laboratory, and tells Alice by the classical channel that all the operations of agents have been finished.

iv) After receiving the message from Zach, Alice encodes the secret M by performing the Pauli operations on the photons of the H-sequence according to the following definitions: I(σ_x, σ_z, iσ_y) corresponds to the two classical bits “00” (“10”,“01”,“11”). Here

Then Alice sends the H⁽¹⁾-sequence (encoded from H-sequence) to Zach.

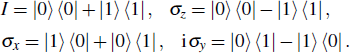v) After receiving the H⁽¹⁾-sequence, Zach together with other agents firstly performs the eavesdropping detection with Alice. First Alice chooses randomly k₁ positions of T⁽ⁿ⁾-sequence to tell all the agents. Then the agents choose randomly a delegate (like Green) to collect the others’ messages of operations on the chosen photons and to perform the reverse compound operations deduced by these messages. Then Green measures these photons associated with the corresponding photons of the H⁽¹⁾-sequence in the Bell-basis, and sends the measuring results to Alice. According to the results and the initial states of corresponding Bell states, Alice deduces the corresponding operations and judges whether the photons are attacked by comparing them with the corresponding messages of the secret. If so, the communication is aborted. Otherwise, Alice announces all of the initial Bell states.

If there is no eavesdropping, all the agents can recover the secret by collaborating together. Similarly, they choose randomly a delegate (like Green) to collect all the agents’ messages of operations. Then Green performs the reverse compound operations deduced by these messages on photons of the T⁽ⁿ⁾-sequence and measures these photons associated with the corresponding photons of the H⁽¹⁾-sequence in the Bell-basis. Finally, he can deduce the secret M, according to both the initial Bell states from Alice and the corresponding measuring results. The structure of the new protocol is depicted in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Structure of the dynamic QSS protocol.

Symbol “” denotes Bell states |φ_i⟩_th (i = 1,2, . . ., k) prepared by Alice; symbol “” represents the new entangled states, the left particle of which the phase shift operations have been performed on by all of the agents, and the right particle of which the Pauli operations have been performed on by Alice.

3.2. Process of dynamic parameters update

Without loss of generality, we suppose that |ϕ⁺⟩_th are the Bell states prepared by Alice, 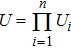is the compound operation on photon t by all the agents and N is the encoding operation on photon h by Alice. At that time, the new entangled state is |φ⟩_th = (U ⊗ N) |ϕ⁺⟩_th. Before Alice sends photon h to agents, two actions are taken as follows.

3.2.1. Update the sub-secret or secret message

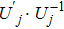
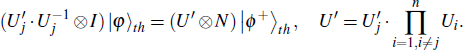(I) Some agent (like Green) wants to update his sub-secret U_j (j = 1, 2, . . ., n). He can ask Zach to send photon t to himself, and then perform operation on it. At that time, the new entangled states have transformed like this

(II) Alice wants to update the secret. She can perform operation N′ · N on photon h. At that time, the new entangled states have transformed like this

3.2.2. Add or delete an agent

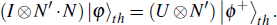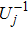
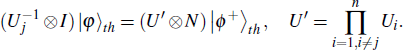I) Some agent (like Green) wants to leave the protocol. He can ask Zach to send photon t to himself, and then perform operation on it. At that time, the new entangled states have transformed like this

II) The new agent (like James) wants to take part in the protocol. Similarly, he can ask Zach to send photon t to himself to perform his own operation U_{n + 1}. At that time, the new entangled states have transformed like this

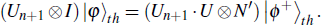If Alice has sent photon h to agents, the secret cannot be updated obviously. Before measuring the entangled states, however, it is allowed to update the sub-secrets of agents, and add or delete an agent.

According to Ref. [29], the QSS protocol is secure if and only if both the sub-secret and secret are secure. Except a series of attacks in the practical views by using the photon number splitter, etc., we will analyze the security of both the sub-secret and secret separately from the theoretical views.

4.2. Security of secret message

There are mainly two kinds of attack strategies on the secret message: one is the compound entanglement swapping attack,^[31–33] and the other is the cheating attack.^[34]

4.2.1. Security against compound entanglement swapping attack

This kind of attack strategy combines an intercept-and-resend attack and entanglement swapping scheme (such as the collective attack^[26]). In these attack strategies,^[31–33] the dishonest agent (such as Eve) or their group can intercept and replace the travel photon (such as photon t) with photon t′ of Bell state |ψ⁻⟩_t′h′, and then send it to the dealer. After the dealer sends back photon t′ with the secret, Eve can associate with other agents to obtain the secret by measuring both photon t′ and h′ of |ψ⁻⟩_t′h′ together. If the eavesdropping detection is coming, Eve can measure both photon t and h′ together and deduce the suitable unitary operations according to the discipline of entanglement swapping, to escape from the detection.

The compound entanglement swapping attack requires two basic conditions: firstly, the agents of the QSS scheme need to send photon t to the dealer after their operations, thus Eve has the opportunity to replace it with fake photon t′; secondly, the fake operations declared by Eve must be contained in the unitary operations set of the QSS protocol so that the lies can escape from the eavesdropping detections. Correspondingly, there are two effective means against this kind of attack: firstly, modify the structure of the QSS protocol without sending any photons to the dealer, so that it is useless for Eve to replace the travel photon t; secondly, restrict Eve’s announcements, so that she cannot declare the proper unitary operations to hide her behaviors in the process of detections.

The protocol can resist the kind of attack by using the new structure and the phase shift operation set. Firstly, in our QSS protocol the dealer does not ask agents to send photon t back, but encodes the secret on photon h and then sends it to agents. Secondly, the phase shift operation set S = {U(0),U(2π/3),U(4π/3)} can restrict the fake announcements.^[24] Suppose that S′ is the fake operation set, and all elements of S and their compositions may establish the multiplicative group (S). It is easy to know S = (S), then

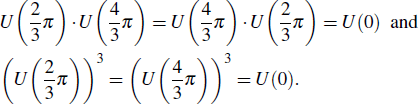It has been demonstrated that S′ ⊄ (S) in Ref. [29]. Thus, the fake operations cannot be deduced by all elements of S and their behaviors cannot escape from the detections.

4.2.2. Security against cheating attack

A cheating attack from a dishonest agent^[34] is as follows. In the secret reconstruction phase, the dishonest agent may provide a false share so that the secret cannot be recovered correctly by the authorized groups but he can correct the error alone. At present, most schemes cannot resist this attack. Only by using the verifiable QSS scheme,^[34] can authorized groups resist an attack by verifying the truth of shares.

Our protocol can also resist this cheating attack by utilizing the phase shift operation set S = {U(0),U(2π/3),U(4π/3)}. Suppose that |ϕ⁺⟩ is the Bell states prepared by Alice, and Eve is a dishonest agent who performed the unitary operation U(α) ∈ S on photon t in Step 2 or 3. However, she provides the false operation message U(β) ≠ U(α) in Step 5. If the compound operation of other agents is U(θ), and the encoding operation of Alice on photon h is N, thus [(U⁻¹(β + θ) · U(α + θ)) ⊗ N]|ϕ⁺⟩_th ≠ (I ⊗ N) |ϕ⁺⟩_th, and N ∈ {I, σ_x, σ_z, iσ_y}.

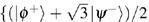
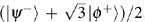
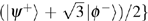
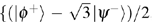
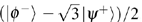
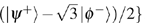
Now, the entanglement states cannot be located in the basis {|ϕ⁺⟩, |ϕ⁻⟩, |ψ⁺⟩, |ψ⁻⟩}, but in the basis , , , or , , , . Obviously the two bases are non-orthogonal with the Bell basis. If Eve provides the false share for recovery, the authorized group of agents will choose the wrong measurement basis. According to the uncertainty principle, the measurement result about the entanglement states will inevitably be distributed in error states randomly, so that Eve cannot correct and obtain the secret from the error because of the irreversibility of measurement. Therefore, the protocol can resist an in-attacker’s cheating attack.

The new DQSS protocol is more efficient than previous ones.

Firstly, the two-particle transform of Bell states is based on a quantum dense-coding scheme. Thus we can transmit the 2-bit classical message by performing an operation on 1 qubit in this protocol.

Secondly, the elements of the set S = {U(0),U(2π/3), U(4π/3)} satisfy the commutative principle of multiplication. Suppose ∀α, β ∈ {0,2π/3,4π/3}, then

So the agents need not consider the order of agents’ local unitary operations in step 2 or 3 but just do the addition to deduce the compound operation of all agents. Suppose that Bob_i (i = 1, . . ., n) performs unitary operations U⁽ⁱ⁾ = U(θ_i) on the photon t, where θ_i ∈ {0,2π/3,4π/3}. The compound operation of all agents is

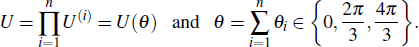Thus it reduces the computation complexity of secret reconstruction to O(n − 1). It not only provides convenience to the secret reconstruction phase, but also improves the efficiency of the scheme.

Thirdly, the unitary operation set S has the least number of elements on the premise of satisfying the conditions of security, which improves further the efficiency for recovering the secret. According to the conclusions in Refs. [35] and [36], if the elements of set S constitute a multiplicative group (S), the number of elements of (S) must be no less than 3, or else elements of (S) can be distinguished during performing them on a suitable single-particle state or one particle of an entangled state, which cannot satisfy the conditions of security. Obviously, the number of elements of (S) reaches the lower bound: (S) = S = {U(0),U(2π/3),U(4π/3)}.

The detailed comparisons between the new protocol and some existing ones are presented in Table 1.

Table 1.

Table 1.

Table 1. Comparisons between new protocol and some existing ones . Issue\protocol Yang’s protocol[21] Jia’s protocol[22] Hsu’s protocol[23] The new protocol The total number of photons 2 mk+k′ k(2n+1)+k′ 2k(n+1)+k′ 2k The times of encoding operations 2n(n − 1)k / / k The complexity of secret reconstruction O(nt) / / O(n − 1)

Table 1. Comparisons between new protocol and some existing ones .

Suppose that the length of the secret message is 2k bit, and the total number of sample photons used for detections will be k′ bit.

According to Ref. [20], we can also present a kind of DSSQS protocol based on the new protocol above, the DQSS protocol for two-particle maximum entangled states, which is as secure as the former, and similarly has the functions of dynamic parameter update: adding or deleting an agent and updating sub-secrets. Here we just brief it as follows:

Suppose that the unknown two-particle maximum entangled state is |φ⟩₁₂ = α|+x⟩₁ |+ y⟩₂ + β|−x⟩₁ |−y⟩₂ (α² + β² = 1). Similarly, Alice prepares two pairs of Bell states (like |φ₁⟩_th and |φ₂⟩_th), one of which is used for the quantum entanglement swapping from Alice to Bob, the other is used to send the classical message of the Bell-state measuring result on both |φ⟩ and one particle of |φ₂⟩_th to other agents by use of the DQSS protocol we just proposed. In the secret reconstruction phase, Bob and other agents must collaborate together to reconstruct the unknown single quantum state. Moreover, this protocol can expand straightly into the one for unknown GHZ states. The structure of the DSSQS protocol for two-particle maximum entangled states is depicted in Fig. 2.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Structure of the DSSQS protocol for two-particle maximum entangled states.

Symbol “” denotes unknown two-particle entangled state |φ⟩₁₂; symbol “” represents Bell states |φ₁⟩_th or |φ₂⟩_th prepared by Alice; symbol “” refers to new entangled states, the left particle of which the phase shift operations have been performed on by agents except Bob, and the right particle of which Pauli operations have been performed on by Alice.

To summarize, firstly, we have proposed the two-particle transform of Bell states, and then presented a novel DQSS protocol for classical messages and DSSQS protocols based on the former one. Compared with the existing QSS protocol, this kind of QSS protocol is not only more secure and efficient, but also has the functions of a dynamic parameter update. Besides, our protocols are merely the (n,n) threshold protocols, which can be described by the fact that at least n agents must combine their sub-secrets together to recover the secret, and we will propose the (t,n) threshold protocol (with t ˂ n) in the coming paper. Furthermore, the two-particle transform of Bell states may also have potential impacts on quantum key distribution,[37,38] quantum secure direct communication, quantum signature, and quantum secure multiparty computation, and so on, which is worth further exploration.